Ⅰ. Introduction
Fractional-order dynamic system has received a
growing interest due to the fact that many real-world physical
systems can be well characterized by fractional-order state
equations and modeling various physical phenomena involves less
parameters than traditional integer-order system [1]. Many
useful analysis and synthesis results about fractional-order systems
have emerged,such as stability [2, 3, 4] and Mittag-Leffler
stability analysis [5],robust stability [6, 7],$H_\infty$
performance analysis [8],$H_\infty$ feedback
control [9, 10, 11],and so on.
On the other hand,the Kalman-Yakubovich-Popov (KYP) Lemma has been
proved to be a very strong tool to convert frequency domain
inequalities (FDIs) to linear matrix inequalities (LMIs) [12]. Many control methods have been developed with the help of KYP
Lemma [13, 14, 15]. However,KYP Lemma just only characterizes FDIs
in entire frequency range and does not deal with the multiple FDIs
in finite range. The generalized Kalman-Yakubovich-Popov (GKYP)
Lemma provided in [16] extends the standard KYP Lemma to present the
LMI characterization of FDIs in finite frequency range. It has been
shown that the GKYP Lemma is profitable for system dissipative
analysis and control synthesis problems which can be exactly
converted to semidefinite programming or convex optimization
problems. Based on GKYP Lemma,$H_\infty$ model reduction [17]
and static output feedback control [18] problem for
integer-order systems have been investigated over finite frequency. Furthermore,the $H_\infty$ performance analysis and $H_\infty$
control synthesis for fractional-order systems have been also
considered in [8, 9, 19, ]. But these results are presented over the
entire frequency range. It is worth noting that the $H_\infty$
synthesis problems over a finite frequency range is essentially
different from the entire frequency range case this is because even
the state feedback control problem cannot be completely solved via
convex optimization [17].
In this paper,we will investigate the problem of $H_\infty$ static
output feedback (SOF) controller synthesis for linear time-invariant
fractional-order systems subject to finite frequency range. Based on
the GKYP Lemma and a key projection lemma,necessary and sufficient
condition is firstly established for the existence of a SOF
controller that ensures the fractional order system is
asymptotically stable and satisfies the prescribed $H_\infty$
performance index over a finite frequency range. Then,by using
matrix congruence transformation,the feedback gain matrix is
decoupled from matrix variables and parameterized by a scalar
matrix. Moreover,two iterative algorithms are developed to solve
this problem. Finally,numerical examples are given to demonstrate
the effectiveness of our proposed method.
Notations. For a matrix $M$,its transpose and complex
conjugate transpose are denoted by $M^{\rm T}$,$M^*$,respectively. The symbol $ H_n$ stands for the set of $n\times n$ Hermitian
matrices. For a matrix $M\in {\bf H}_n$,inequalities $M>0$ $(\ge
0)$ and $M$ $<$ $0$ $(\le 0)$ denote positive (semi) definiteness
and negative (semi) definiteness,respectively. For matrices $\Phi$
and $P$,$\Phi\otimes P$ means the Kronecker product. All the
matrices are assumed to be of compatible dimensions and $\ast$ is
used to denote the Hermitian part. For any matrix $M\in {\bf
C}^{n\times n}$,${\rm Her}(X)=X$ $+$ $X^*$. ${\rm Re}(M)$
represents the real parts of the complex matrix $M$. For $G\in {\bf
C}^{n\times m}$ and $\Pi\in {\bf H}_{n+m} $,a function $\sigma:
{\bf C}^{n\times m}$ $\times$ ${\bf H}_{n+m}$ $\to$ ${\bf H}_{m}$ is
defined by
|
\begin{eqnarray*}
\sigma (G,\Pi):=\left[\begin{array}{l}
G\\I_m\end{array}\right]^*\Pi\left[\begin{array}{l}
G\\I_m\end{array}\right].
\end{eqnarray*}
|
|
${\rm j}$ denotes the imaginary unit.
Ⅱ. Preliminaries
In this paper, taking the physical meaning into consideration, the
Caputo fractional-order derivative is used and defined as follows:
|
\begin{align*}
D^{\alpha}f(t)=\frac{{\rm d}^{\alpha}f(t)}{{\rm d}t^{\alpha}}=
\frac{1}{\Gamma(m-\alpha)}\int_{0}^{t}\frac{f^{(m)}(\tau)}{(t-\tau)^{\alpha+1-m}}{\rm
d}\tau,
\end{align*}
|
|
where $f(t)$ is a time-dependent function,$\alpha$ represents the
order of the derivative ($m - 1 \le \alpha < m$, $m$ is an integer).
Consider the following linear time-invariant fractional-order system admitting a pseudo state space representation of the form
|
\begin{align}\label{system model}
\begin{cases}
D^{\alpha}x(t)=Ax(t)+B_{1}u(t)+Bw(t),\\[1mm]
z(t)=C x(t)+Dw(t),\\[1mm]
y(t)=C_{y}x(t),
\end{cases}
\end{align}
|
(1) |
where $\alpha$ is the fractional order and $\alpha\in (0,\ 2)$. $x(t)\in {\bf R}^{n}$ is system state,$u(t)\in {\bf R}^m$ is
control input,$w(t)\in {\bf R}^{q}$ is disturbance input,$z(t)\in
{\bf R}^{s}$ is control output,$y(t)\in{\bf R}^l$ is measured
output. $A\in {\bf R}^{n\times n}$,$B_1\in {\bf R}^{n\times m}$,
$B\in {\bf R}^{n\times q}$,$C$ $\in$ ${\bf R}^{s\times n}$,$C_y\in
{\bf R}^{l\times n}$,and $D \in {\bf R}^{s\times q}$ are known
matrices.
In general,the frequency ranges can be visualized as the following set of complex numbers that represents certain curves on the complex plane:
|
\begin{eqnarray}\label{cv}
\Lambda(\Phi,\Psi):=\{\lambda\in {\bf C}|
\sigma(\lambda,\Phi)=0,\sigma(\lambda,\Psi)\geq 0\},
\end{eqnarray}
|
(2) |
where $\Phi$,$\Psi\in{\bf H}_2$.
Define $\bar{\Lambda}(\Phi,\Psi)=\Lambda(\Phi,\Psi)\cup\{ \infty\}$ if $\Lambda$ is bounded,otherwise $\bar{\Lambda}(\Phi,\Psi)=\Lambda(\Phi,\Psi)$.
By choosing appropriate $\Phi$ and $\Psi$ in (2),the set
$\Lambda(\Phi,\Psi)$ can be specified to define a certain range of
the frequency curve. For fractional-order system,we can choose
|
$$\Phi=\left[\begin{array}{cc} 0 & r\\ \ast & 0\end{array}\right] $$
|
|
to represent the curve $\Lambda=\{ ({\rm j}\omega)^\alpha| \omega\in
\Omega\}$,where $r={\rm e}^{{\rm j}\theta}$,$\theta$ $=$
$(\alpha-1)\pi/2$,$\Omega$ is a subset of real numbers specified by
appropriate choice of $\Psi$,Table Ⅰ shows an example.
Table Ⅰ
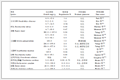
Table Ⅰ
CHOICE OF $\Psi$ FOR DIFFERENT FREQUENCY RANGES
|
Table Ⅰ
CHOICE OF $\Psi$ FOR DIFFERENT FREQUENCY RANGES
|
In Table Ⅰ,$\omega_c:=({\omega_l^\alpha+\omega_h^\alpha})/{2}$,
$\omega_h\geq 0$,$\omega_l\geq 0$,and HF,MF and LF denote high,
middle and low frequency ranges,respectively.
In this paper,we focus on the static output feedback controller in the following form:
|
\begin{align}
u(t)=Ky(t),
\end{align}
|
(3) |
then,we have the following closed-loop system
|
\begin{align}
\begin{cases}
D^{\alpha}x(t)=\hat{A}x(t)+B\omega(t),\\[1mm]
z(t)=C x(t)+D\omega(t),
\end{cases}
\end{align}
|
(4) |
where $\hat{A}=A+B_{1}KC_{y}$.
Therefore,the finite frequency $H_{\infty}$ static output feedback control problem can be formulated as follows.
Problem FF-${\pmb H_{\pmb\infty}}$-SOFC (Finite frequency
${\pmb H}_{\pmb\infty}$ static output feedback control) For a
pre-specified frequency range $\Lambda(\Phi,\Psi)$ and a given
performance index $\gamma>0$,The problem of the $H_{\infty}$ static
output feedback control over frequency range $\Lambda(\Phi,\Psi)$
is to find a static output feedback controller (2) such that:
1) The closed-loop system (3) is asymptotically stable.
2) The transfer function $G(s)$ of closed-loop system (3) satisfies
the finite frequency $H_{\infty}$ performance ${\rm
sup}_{\omega\in\Lambda(\Phi,\Psi)}\bar\sigma(G({\rm j}\omega))<
\gamma$,where $G(s)=C(s^\alpha I- \hat A)^{-1}B+D$,$\bar\sigma$
denotes the maximum singular value of a matrix.
The following lemma is very useful in the proofs of the main results of this paper.
Lemma 1 [11] Let $A\in {\bf R}^{n\times n}$,the linear
time-invariant system $D^{\alpha}x(t)=Ax(t)$ with $\alpha\in(0,
1)$ is asymptotically stable if and only if there exists Hermitian
matrix $H>0$ such that $({\rm Re}(rH))^{\rm T}A^{\rm T}+A({\rm
Re}(rH))<0$.
Lemma 2 [11] Let $A\in {\bf R}^{n\times n}$,the linear
time-invariant system $D^{\alpha}x(t)=Ax(t)$ with $\alpha\in(1,
2)$ is asymptotically stable if and only if there exists Hermitian
matrix $H>0$ such that $rHA^{\rm T}+\bar{r}AH<0$.
Lemma 3~(GKYP Lemma) [16, 19] Given real matrices $A$,
$B$,$C$,$D$,a real symmetric matrix $\Pi$,and $\Phi$,$\Psi$,
$\in {\bf H}_2$,let $G(\lambda)=C(\lambda I-A)^{-1}B+D$. Then the
frequency range inequality
|
\begin{eqnarray*}
\left[\begin{array}{c} G(\lambda)\\ I\end{array}\right]^*\Pi \left[\begin{array}{c} G(\lambda)\\ I\end{array}\right]<0
\end{eqnarray*}
|
|
holds for all $\lambda\in \bar{\Lambda}(\Phi,\Psi)$ if and only if there exist Hermitian matrices $P$ and $Q>0$ such that
|
\begin{align*}
&\left[\begin{array}{cc} A & I\\C & 0\end{array}\right](\Phi \otimes
P+\Psi \otimes Q)\left[\begin{array}{cc} A & I\\C &
0\end{array}\right]^{\rm T}\\&\qquad +\left[\begin{array}{cc} B&
0\\D & I\end{array}\right]\Pi\left[\begin{array}{cc} B& 0\\D &
I\end{array}\right]^{\rm T}<0.
\end{align*}
|
|
Remark 1. Let
|
$$\Pi=
\left[
\begin{array}{cc}
I & 0 \\
0 & \gamma^2 I
\end{array}
\right]
$$
|
|
or
|
$$\Pi=
\left[
\begin{array}{cc}
0 & -I \\
-I & 0
\end{array}
\right],
$$
|
|
the characterization of Lemma 3 turns into the bounded real lemma
and positive real lemma.
Lemma 4~ (Projection Lemma) [20] Given a symmetric matrix
$\Xi\in {\bf R}^{m\times m}$ and two matrices $P$,$Q$ of column
dimension $m$,consider the problem of finding some matrix $\Theta$
of compatible dimensions such that
|
\begin{eqnarray}\label{Projection LMI}
\Xi+P^{\rm T}\Theta^{\rm T}Q+Q^{\rm T}\Theta P<0.
\end{eqnarray}
|
(5) |
Denote by $ \aleph_P$,$ \aleph_Q$ any matrices whose columns form basis of the null space of $P$ and $Q$,respectively. Then (5) is solvable for $\Theta$ if and only if
|
\begin{align*}
\begin{cases}
\aleph^{\rm T}_P\Xi \aleph_P < 0,\\[1mm]
\aleph^{\rm T}_Q\Xi \aleph_Q <0.\end{cases}
\end{align*}
|
|
Ⅲ. Main results
In this section,we will firstly investigate the $H_{\infty}$ static
output feedback control for fractional-order systems over middle
frequency ranges. Based on the GKYP Lemma and the projection
lemma,we will give the necessary and sufficient condition that the
problem of FF-$H_{\infty}$-SOFC is solvable.
Theorem 1. Given performance index $\gamma>0$,fractional
order $\alpha\in(0,1)$,system matrices $A,B_{1},B,C,D,C_{y}$,a
feedback gain $K$ and finite frequency range
$\Lambda_{MF}=\{\omega\in {\bf R}:$ $\omega_{l}$ $\leq$ $\omega$
$\leq$ $\omega_{h}$,$\omega_{l},\omega_{h}\geq0\}.$ Problem
FF-$H_{\infty}$-SOFC is solvable if and only if there exist
Hermitian matrices $H>0$,$Q>0$,$P$,and real matrix $E=[E_{1},\
E_{2}]$ such that the following matrix inequalities hold:
|
\begin{eqnarray}\label{LMI1}
\Xi={\rm Her}({ \hat{A}({\rm Re}(rH))})<0,
\end{eqnarray}
|
(6) |
and
|
\begin{eqnarray}\label{LMI2}
\Sigma=\left[
\begin{array}{cccc}
-Q & \Sigma_{12} &-E_{2} &0 \\
\ast & \Sigma_{22} & \Sigma_{23} & B \\
\ast & \ast & \Sigma_{33} & D\\
\ast & \ast & \ast & -I\\
\end{array}
\right]<0,
\end{eqnarray}
|
(7) |
where $r={\rm e}^{{\rm j}\theta}$,$\theta=(\alpha-1)\pi/2$,$
\hat{A}=A+B_{1}KC_{y},$ and
|
$$\eqalign{
& {\Sigma _{12}} = rP + {\rm{j}}r{\omega _c}Q - {E_1}, \cr
& {\Sigma _{22}} = - \omega _l^\alpha \omega _h^\alpha Q + {\rm{Her}}(\hat A{E_1}), \cr
& {\Sigma _{23}} = \hat A{E_2} + E_1^{\rm{T}}{C^{\rm{T}}}, \cr
& {\Sigma _{33}} = - {\gamma ^2}I + {\rm{Her}}(C{E_2}). \cr} $$
|
|
Proof. (Necessity). It follows from Lemma 1 and Lemma 3
that the problem of FF-$H_{\infty}$-SOFC is solvable if and only
if there exist Hermitian matrices $H>0$,$Q>0$ and $P$ such that
the following matrix inequalities hold. That is,
|
\begin{eqnarray*}
\Xi={\rm Her}({ \hat{A}({\rm Re}(rH))})<0,
\end{eqnarray*}
|
|
and
|
\begin{align*}
&\left[
\begin{array}{cc}
\hat{A} & I \\
C & 0 \\
\end{array}
\right]\left[
\begin{array}{cc}
-Q & r P+{\rm j}r\omega_{c}Q \\
\bar{r}P-{\rm j}\omega_{c}Q & -\omega_{l}^\alpha\omega_{h}^\alpha Q \\
\end{array}
\right]\left[
\begin{array}{cc}
\hat{A} & I \\
C & 0 \\
\end{array}
\right]^{\rm T}\\[1mm]
&\qquad +\left[
\begin{array}{cc}
B & 0 \\
D & I \\
\end{array}
\right]\left[
\begin{array}{cc}
I & 0 \\
0 & -\gamma^{2}I \\
\end{array}
\right]\left[
\begin{array}{cc}
B & 0 \\
D & I \\
\end{array}
\right]^{\rm T}\\[1mm]
&\qquad =\left[
\begin{array}{ccc}
\hat{A} & I & 0 \\
C & 0 & I \\
\end{array}
\right]\Theta\left[
\begin{array}{ccc}
\hat{A} & I & 0 \\
C & 0 & I \\
\end{array}
\right]^{\rm T}<0,
\end{align*}
|
|
where
|
\begin{eqnarray*}
\Theta=\left[
\begin{array}{ccc}
-Q & r P+{\rm j}r\omega_{c}Q & 0 \\
\ast & -\omega_{l}^\alpha\omega_{h}^\alpha Q+BB^{\rm T} & BD^{\rm T} \\
\ast & \ast & DD^{\rm T}-\gamma^{2}I \\
\end{array}
\right].
\end{eqnarray*}
|
|
Note that
|
\begin{eqnarray*}
\left[
\begin{array}{ccc}
I & 0 & 0 \\
\end{array}
\right]\Theta\left[
\begin{array}{ccc}
I & 0 & 0 \\
\end{array}
\right]^{\rm T}=-Q<0,
\end{eqnarray*}
|
|
and denote that
|
\begin{eqnarray*}
\Gamma=\left[
\begin{array}{ccc}
-I & \hat{A}^{\rm T} & C^{\rm T} \\
\end{array}
\right],\ \
\Lambda= \left[
\begin{array}{ccc}
0 & I & 0 \\
0 & 0 & I \\
\end{array}
\right],
\end{eqnarray*}
|
|
then, we can obtain
|
\begin{eqnarray*}
\aleph_{\Gamma}=\left[
\begin{array}{cc}
\hat{A}^{\rm T} & C \\
I & 0 \\
0 & I \\
\end{array}
\right],\ \ \aleph_{\Lambda}=\left[
\begin{array}{ccc}
I & 0 & 0 \\
\end{array}
\right]^{\rm T},
\end{eqnarray*}
|
|
and
|
\begin{eqnarray*}
\aleph_{\Gamma}^{\rm T}\Theta\aleph_{\Gamma}<0,\ \ \aleph_{\Lambda}^{\rm T}\Theta\aleph_{\Lambda}<0.
\end{eqnarray*}
|
|
It follows from the projection lemma that there exists a real matrix $E=[E_1\ E_2]$ such that
|
\begin{eqnarray*}
\Theta+\Gamma^{\rm T}E\Lambda+\Lambda^{\rm T}E^{\rm T}\Gamma<0,
\end{eqnarray*}
|
|
which implies $\Sigma<0$ holds by Schur complement lemma.
(Sufficiency). It follows from Schur complement lemma that
$\Xi_2<0$ is equivalent to $\Theta+\Gamma^{\rm
T}E\Lambda+\Lambda^{\rm T}E^{\rm T}\Gamma<0$. Using the projection
lemma,$\aleph_{\Gamma}^{\rm T}\Theta\aleph_{\Gamma}<0$ holds. Therefore, the sufficiency is trivially true.
Remark 2. In the above theorem,the feedback gain $K$ is
coupled with matrix variables and is intrinsically non convex. In the following theorem,the feedback gain matrix $K$ will be
decoupled from matrices $H$,$E_{1}$,and $E_{2} $,
simultaneously,and will be parameterized by a positive scalar
matrix.
Theorem 2. Given performance index $\gamma>0$,fractional
order $\alpha\in(0,1)$,system matrices $A$,$B_{1}$,$B$,$C$,$D$
and $C_{y},$ and the finite frequency range
$\Lambda_{MF}=\{\omega\in {\bf R}:\omega_{l}\leq\omega\leq$
$\omega_{h}$,$\omega_{l},\omega_{h}\geq0\}.$ Problem
FF-$H_{\infty}$-SOFC is solvable if and only if there exist
Hermitian matrices $H>0$,$Q>0$,$P$,real matrices $E=[E_{1},\
E_{2}]$,$U$,and a scalar $\epsilon>0$,such that the following
matrix inequalities hold
|
\begin{eqnarray}\label{LMI3}
\bar{\Xi}=\left[
\begin{array}{cc}
\bar{\Xi}_{11} & -({\rm Re}(rH))^{\rm T}-B_{1}LC_{y} \\
\ast & -\epsilon I \\
\end{array}
\right]<0,
\end{eqnarray}
|
(8) |
and
|
\begin{eqnarray}\label{LMI4}
\bar{\Sigma}= \left[
\begin{array}{ccccc}
-Q & \bar{\Sigma}_{12} & -E_{2} & 0 & 0 \\
\ast & \bar{\Sigma}_{22}& \bar{\Sigma}_{23} & B & \bar{\Sigma}_{25} \\
\ast & \ast & \bar{\Sigma}_{33} & D & -E_{2}^{\rm T} \\
\ast & \ast & \ast & -I & 0 \\
\ast & \ast & \ast & \ast & -\epsilon I \\
\end{array}
\right]<0,
\end{eqnarray}
|
(9) |
where $r={\rm e}^{{\rm j}\theta}$,$\theta=(\alpha-1)\pi/2$,
and
|
\begin{align*}
\bar{\Xi}_{11}=&\ {\rm Her}\left( A({\rm Re}(rH))-B_1LC_{y}U^{\rm T}B_1^{\rm T}\right)\\
&\,+\epsilon B_1UU^{\rm T}B_1^{\rm T},\\[1mm]
\bar{\Sigma}_{12}=&\ rP+{\rm j}r\omega_{c}Q-E_{1},\\[1mm]
\bar{\Sigma}_{22}=&\,-\omega_{l}^\alpha\omega_{h}^\alpha Q+{\rm Her}(AE_1-B_1LC_{y}U^{\rm T}B_1^{\rm T})\\
&\,+\epsilon B_1UU^{\rm T}B_1^{\rm T},\\[1mm]
\bar{\Sigma}_{23}=&\ AE_{2}+E_{1}^{\rm T}C^{\rm T},\\[1mm]
\bar{\Sigma}_{33}=&\,-\gamma^{2}I+{\rm Her}(CE_{2}),\\[1mm]
\bar{\Sigma}_{25}=&\,-E_{1}^{\rm T}-B_1LC_{y}.
\end{align*}
|
|
Moreover,the static output feedback control gain is designed as $K=\epsilon^{-1} L$.
Proof. (Necessity). It follows from Theorem 1 that problem FF-$H_{\infty}$-SOFC is solvable
if and only if there exist Hermitian matrices $H>0$,$Q>0$,$P$ and real matrix $E=[E_{1},E_{2}]$ such that (6) and
(7) hold. It is always possible to find a sufficiently large scalar $\epsilon$ such that
|
\begin{eqnarray*}
\left[
\begin{array}{cc}
{\rm Her}(\hat{A}({\rm Re}(rH))) &-{\rm Re}(rH)^{\rm T} \\
\ast & -\epsilon I \\
\end{array}
\right]<0,\,\
\end{eqnarray*}
|
|
and
|
\begin{eqnarray*}
\left[
\begin{array}{cc}
\Xi_2 & \Upsilon^{\rm T}\\
\ast & -\epsilon I \\
\end{array}
\right]<0,
\end{eqnarray*}
|
|
where $\Upsilon=[0\ -E_{1}\ -E_{2}\ \ 0]$.
Taking congruence transformation yields
|
\begin{align}\label{tilder xi1}
& \Gamma_{1}^{\rm T}\ \left[
\begin{array}{cc}
{\rm Her}(\hat{A}({\rm Re}(rH))) & -({\rm Re}(rH) )^{\rm T} \\
\ast & -\epsilon I \\
\end{array}
\right]\Gamma_{1}\nonumber\\[1mm]
&\qquad = \left[
\begin{array}{cc}
\Phi_{11} &\Phi_{12} \\
\ast & -\epsilon I \\
\end{array}
\right]<0.
\end{align}
|
(10) |
with
|
\begin{align*}
&\Gamma_{1}=\left[
\begin{array}{cc}
I & 0 \\
(B_{1}KC_{y} )^{\rm T}& I \\
\end{array}
\right],\\[1mm]
& \Phi_{11}={\rm Her}( A({\rm Re}(rH))-\epsilon (B_{1}KC_{y})(B_{1}KC_{y})^{\rm
T},\\[1mm]
& \Phi_{12}=-({\rm Re}(rH))^{\rm T}-\epsilon B_{1}KC_{y}.
\end{align*}
|
|
Let $\epsilon K=L$
and note that
|
$$B_1(LC_{y}-\epsilon U)\epsilon^{-1}(LC_{y}-\epsilon U)^{\rm T}B_1^{\rm T}\geq0$$
|
|
holds for any real matrix $U$. Expanding this inequality,one has
|
\begin{align}\label{add ineq}
&-(B_1LC_{y})\epsilon^{-1}(B_1LC_{y})^{\rm T}\nonumber\\[1mm]
&\qquad
\leq-B_1LC _{y}U ^{\rm T}B_1^{\rm T}-B_1U(LC_{y})^{\rm T}B_1^{\rm
T}+\epsilon B_1UU^{\rm T}B_1^{\rm T}.
\end{align}
|
(11) |
Using above inequality and combining (10),we get (8). In the same way,taking congruence transformation,
we have
|
$$\Gamma_{2}^{\rm T}\left[
\begin{array}{cc}
\Xi_2 & \Upsilon^{\rm T} \\
\ast & -\epsilon I \\
\end{array}
\right]\Gamma_{2}<0,$$
|
|
with
|
$$ \Gamma_{2}=\left[
\begin{array}{ccccc}
I & 0 & 0 & 0 & 0 \\
0 & I & 0 & 0 & 0 \\
0 & 0 & I & 0 & 0 \\
0 & 0 & 0 & I & 0 \\
0 & (B_{1}KC_{y})^{\rm T} & 0 & 0 & I \\
\end{array}
\right].$$
|
|
Let $\epsilon K=L$ and use inequality (11),we get (9).
(Sufficiency). Suppose that there exist Hermitian matrices $H>0$,
$Q>0$,$P$,real matrices $E=[E_{1},\ \ E_{2}]$,$U$ and a scalar
$\epsilon>0$ such that (8) and (9) hold. From
(11), (8) implies that
|
\begin{eqnarray*}
\left[
\begin{array}{cc}
\tilde{\Phi}_{11} & - ({\rm Re}(rH))^{\rm T}-B_{1}LC_{y}\\
\ast & -\epsilon I \\
\end{array}
\right]<0,
\end{eqnarray*}
|
|
where
|
$$\tilde{\Phi}_{11}={\rm Her}( A({\rm Re}(rH))-(B_1LC_{y})\epsilon ^{-1}(LC_{y})^{\rm T}B_1^{\rm T},$$
|
|
choosing $U=\epsilon ^{-1}LC_{y}$ yields
|
\begin{eqnarray*}
\left[
\begin{array}{cc}
\bar{\Phi}_{11} & -({\rm Re}(rH))^{\rm T}-\epsilon B_{1}U\\
\ast & -\epsilon I \\
\end{array}
\right]<0,
\end{eqnarray*}
|
|
where,$\bar{\Phi}_{11}={\rm Her}( A({\rm Re}(rH))-\epsilon B_1UU^{\rm T}B_1^{\rm T} $.
Therefore,using congruence transformation and letting
$\epsilon^{-1}L$ $=$ $K$,we can conclude that
|
\begin{eqnarray*}
\left[
\begin{array}{cc}
{\rm Her}(\hat{A}({\rm Re}(rH))) &-({\rm Re}(rH))^{\rm T} \\
\ast & -\epsilon I \\
\end{array}
\right]<0,
\end{eqnarray*}
|
|
and $ {\rm Her}(\hat{A}({\rm Re}(rH))) <0$. Similarly,one can
deduce that (9) implies (7).
Remark 3.
Based on congruence transformation,the feedback gain $K$ can be decoupled from $H$,$E_{1}$ and $E_{2}$ simultaneously,
and parameterized by a positive scalar $\epsilon$. Note that the matrix inequalities in (8) and (9) are still bilinear,
however,we can fix $U$ to make them linear. Using the method provided in [21, 22],we defined $\eta\in {\bf R}$ satisfying that
|
\begin{align*}
\begin{cases}
\bar{\Xi}-{\rm diag}\{\eta I,0\}<0,\\[1mm]
\bar{\Sigma}-{\rm diag}\{0,\eta I,0,0,0\}<0.\\
\end{cases}
\end{align*}
|
|
It is easily known from the proof of Theorem 1 that $\eta$
achieves its minimum when $U=\epsilon^{-1}LC_{y}$,which naturally
leads to an iterative LMI (ILMI) algorithm.
Algorithm 1 (ILMI algorithm).
Step 1. Set $j=1$. For a given $H_{\infty}$ performance level
$\gamma>0$,and the finite frequency range $\Lambda_{FF}=\{\omega\in
{\bf R}:\omega_{l}\leq\omega\leq$ $\omega_{h}$,$\omega_{l},
\omega_{h}\geq0\}$. Solve the following relaxed LMIs
|
\begin{eqnarray}\label{LMI5}
{\rm Her}(A({\rm Re}(rH))+B_{1}W_{1})<0,
\end{eqnarray}
|
(12) |
and
|
\begin{eqnarray}\label{LMI6}
\left[
\begin{array}{cccc}
-Q & \hat{\Phi}_{12} & -E_{2} & 0 \\
\ast & \hat{\Phi}_{22} & \hat{\Phi}_{23} & B \\
\ast &\ast & \hat{\Phi}_{33} & D \\
\ast &\ast &\ast & -I \\
\end{array}
\right]<0.
\end{eqnarray}
|
(13) |
where
|
\begin{align*}
\hat{\Phi}_{12}&=r P+{\rm j}r\omega_{c}Q-E_{1},\\[1mm]
\hat{\Phi}_{22}&=-\omega_{l}^\alpha\omega_{h}^\alpha Q+{\rm Her}(AE_{1}+B_{1}W_{2}),\\[1mm]
\hat{\Phi}_{23}&=AE_{2}+B_{1}W_{3}+E_{1}^{\rm T}C^{\rm T},\\[1mm]
\hat{\Phi}_{33}&=-\gamma^{2}I+Her(CE_{2}),
\end{align*}
|
|
with variables in
$S\triangleq \{$Hermitian matrices $H>0$,$Q>0$,$P$,and real
matrices,$E_{1}$,$E_{2}$,$W_{1}$,$W_{2}$ and $W_{3}\}.$
The initial value $U_{1}$ is obtained as
|
$$U_{1}=W_{1}({\rm Re}(rH))^{-1}.$$
|
|
Step 2. For fixed $U_{j}$,solve the following minimization
problem for matrix variables in the set $S\triangleq\{$Hermitian
matrices $H>0$,$Q>0$,$P,$ real matrices $E=[E_{1},E_{2}]$,$U$
and a scalar $\epsilon>0\}$
|
\begin{align}\label{optimization LMI}
&\min\ \eta,\nonumber\\[2mm]
&\,{\rm s.t.} \begin{cases}
\bar{\Xi}-{\rm diag}\{\eta I,0\}<0,\\
\bar{\Sigma}-{\rm diag}\{0,\eta I,0,0,0\}<0,\\
\end{cases}
\end{align}
|
(14) |
where $\bar{\Xi}$ and $\bar{\Sigma}$ are defined in (8) and (9) respectively. Denote the obtained $\eta$ as $\eta_{j}$.
Step 3. If $\eta_{j}<0,$ then a desired feedback gain is
obtained as $K=\epsilon^{-1} L$.
Step 4. Fix $\eta=\eta_{j}$,minimize $\epsilon$ such that
LMIs (14) hold,denote the obtained
$\epsilon$ and $L$ as $\epsilon_{j}$ and $L_{j}$.
Step 5. If $|\eta_{j}-\eta_{j-1}|/\eta_{j-1}<\tau$,where
$\tau$ is a prescribed tolerance,then this algorithm fails to find
the desired feedback gain $K$,stop; If not,update $\eta_{j+1}$ as
$U_{j+1}=\epsilon_{j}^{-1}L_{j}C_{y}$. Set $j$ $:=$ $j$ $+$ $1$ and
go to Step 2.
Before employing the ILMI algorithm, it is suggested to find some
initial value which is ``close'' to the desired solution. We adopt
the following initial optimization algorithm provided in [11]. Denote $\bar{W}=[W_{1},\ W_{2},\ W_{3}]$ and $\bar{E}=[{\rm
Re}(rH),\ E_{1} ,\ E_{2}]$.
Algorithm 2 (Initial optimisation).
Step 1. Set $j=1$. For a given $H_{\infty}$ performance level
$\gamma>0$,and the finite frequency range $\Lambda_{FF}=\{\omega\in
{\bf R}:\omega_{l}\leq\omega\leq\omega_{h},$ $\omega_{l},
\omega_{h}\geq0\},$ find Hermitian matrices $H>0$,$Q>0$,$P$,
and real matrices $W_{1}$,$W_{2}$,$W_{3}$ such that LMIs
(12}) and (13) hold. Denote the feasible solution
$\bar{E}$ and $\bar{W}$ as $\bar{E_{j}}$ and $\bar{W_{j}}.$
Step 2. Fix $\bar{E}=\bar{E_{j}}$,minimize
$\delta=\|\bar{W}- N\otimes \bar{E}\|_{2},$ such that LMIs
(12) and (13) hold,where $N$ is a real matrix
variable. Denote the obtained $N$ as $N_{j}$.
Step 3. Fix $N=N_{j}$,minimize $\delta=\|\bar{W}-N \otimes
\bar{H}\|_{2},$ such that LMIs (13) and (12) hold. Denote the minimized $\delta$ as $\delta_{j}$.
Step 4. Set $j:=j+1$,and repeat { Step 2} and { Step 3}. If
$|\delta_{j}-\delta_{j-1}|/ \delta_{j-1}\leq \mu$,where $\mu$ is a
prescribed tolerance,then stop. The initial value $U_{1}$ is given
by $U_{1}=W_{1}({\rm Re}(rH))^{-1}$.
Follow the similar line,we can give the condition that the problem of FF-$H_{\infty}$-SOFC is solvable over low frequency range as follows.
Theorem 3. Given performance index $\gamma>0$,fractional
order $\alpha\in(0,1)$,system matrices $A$,$B_{1}$,$B$,$C$,
$D$,$C_{y}$,a feedback gain $K$ and finite frequency range
$\Lambda_{LF}=\{\omega\in$ ${\bf R}:$ $\omega\leq\omega_{l}$,
$\omega_{l}\geq0\}$. Problem FF-$H_{\infty}$-SOFC is solvable if and
only if there exist Hermitian matrices $H>0$,$P$ and $Q$ $>$ $0$,
real matrix $U$,$E=[E_{1},\ E_{2}]$ and real scalar $\epsilon$ such
that the following matrix inequalities hold
|
\begin{eqnarray*}
\tilde{\Xi}=\left[
\begin{array}{cc}
\tilde{\Xi}_{11} & -({\rm Re}(rH))^{\rm T}-B_{1}LC_{y} \\
\ast & -\epsilon I \\
\end{array}
\right]<0,
\end{eqnarray*}
|
|
and
|
\begin{eqnarray*}
\tilde{\Sigma}=\left[\begin{array}{ccccc}
-Q & rP-E_{1} & -E_{2} & 0 & 0\\
\ast & \tilde{\Sigma}_{22} & \tilde{\Sigma}_{23} & B & \tilde{\Sigma}_{25}\\
\ast & \ast & \tilde{\Sigma}_{33} & D & -E_{2}^{\rm T}\\
\ast & \ast & \ast & -I & 0\\
\ast & \ast & \ast & \ast & \epsilon I
\end{array}\right]<0,
\end{eqnarray*}
|
|
where $r={\rm e}^{{\rm j}\theta}$,$\theta=(\alpha-1)\pi/2$,and
|
\begin{align*}
\tilde{\Xi}_{11}=&\ {\rm Her}\left( A({\rm Re}(rH))-B_1LC_{y}U^{\rm T}B_1^{\rm T}\right)\\
&\,+\epsilon B_1UU^{\rm T}B_1^{\rm T},\\[1mm]
\tilde{\Sigma}_{23}=&\ AE_{2}+E_{1}^{\rm T}C^{\rm T},\\[1mm]
\tilde{\Sigma}_{22}=&\ \omega_{l}^{2\alpha}Q+{\rm Her}(AE_{1}-B_{1}LC_{y}U^{\rm T}B_{1}^{\rm T})\\
&\,+\epsilon B_{1}UU^{\rm T}B_{1}^{\rm T},\\[1mm]
\tilde{\Sigma}_{25}=&\,-E_{1}^{\rm T}-B_{1}LC_{y},\\[1mm]
\tilde{\Sigma}_{33}=&\,-\gamma^{2}I+{\rm Her}(CE_{2}).
\end{align*}
|
|
Moreover,the static output feedback control gain is designed as $K=\epsilon^{-1} L$.
For highest frequency case,we can refer to the designed method in
[17] and use the following condition.
Theorem 4. Given performance index $\gamma>0$,fractional
order $\alpha\in(0,1)$,system matrices $A$,$B_{1}$,$B$,$C$,$D$
and $C_{y}$,and the finite frequency range
$\Lambda_{HF}=\{\omega\in {\bf
R}:\omega\geq\omega_{h},\omega_{h}\geq0\}$. Problem
FF-$H_{\infty}$-SOFC is solvable if and only if there exist
Hermitian matrices $H>0$,$P$,and $Q>0$,real matrix $U$,and a
scalar $\epsilon>0$,such that the following matrix inequalities
hold
|
\begin{eqnarray*}
\hat{\Xi}=\left[
\begin{array}{cc}
\hat{\Xi}_{11} & -({\rm Re}(rH))^{\rm T}-B_{1}LC_{y} \\
\ast & -\epsilon I \\
\end{array}
\right]<0,
\end{eqnarray*}
|
|
and
|
\begin{eqnarray*}
\hat{\Sigma}=\left[\begin{array}{ccccc}
\hat{\Sigma}_{11} & \bar{r}PC^{\rm T} & AQ & B & P+rB_{1}LC_{y}\\
\ast & -\gamma^{2}I & CQ & D & 0\\
\ast & \ast & -Q & 0 & rQ\\
\ast & \ast & \ast & -I & 0\\
\ast & \ast & \ast & \ast & -\epsilon I
\end{array}\right]<0,
\end{eqnarray*}
|
|
where $r={\rm e}^{{\rm j}\theta}$,$\theta=(\alpha-1)\pi/2$,and
|
\begin{align*}
\hat{\Xi}_{11}=&\ {\rm Her}\left( A({\rm Re}(rH))-B_1LC_{y}U^{\rm T}B_1^{\rm T}\right)\\
&\,+\epsilon B_1UU^{\rm T}B_1^{\rm T},\\[1mm]
\hat{\Sigma}_{11}=&\ {\rm Her}(rAP-B_{1}LC_{y}U^{\rm T}B_{1}^{\rm T})-\omega_{h}^{2\alpha}Q\\
&\,+\epsilon B_{1}UU^{\rm T}B_{1}^{\rm T}.
\end{align*}
|
|
Moreover,the static output feedback control gain is designed as $K=\epsilon^{-1} L$.
Remark 4. The designed algorithms of $H_\infty$ static
output feedback controller for fractional order system over high
frequency and low frequency ranges can refer to the middle
frequency case and hence is omitted for brevity.
Remark 5. When the problem of FF-$H_{\infty}$-SOFC for
system with the fractional order $\alpha\in[1,2)$ case is
considered,we just need to replace the stability condition based
on Lemma 2. For example,we just replace LMI (8) by
|
\begin{eqnarray*}
\left[
\begin{array}{cc}
\Psi_{11} & -H-\bar{r}B_{1}LC_{y} \\
\ast & -\epsilon I \\
\end{array}
\right]<0,
\end{eqnarray*}
|
|
where $\Psi_{11}={\rm Her}\left( \bar{r}AH-B_1LC_{y}U^{\rm
T}B_1^{\rm T}\right)+\epsilon B_1UU^{\rm T}B_1^{\rm T}.$
Ⅳ. Numerical Example
Example 1. Consider the system (1) with the
following parameters:
|
\begin{align*}
&A=\left[\begin{array}{cc} -8 & -0.8\\-2 & 0.5\end{array}\right],~~
B_1=\left[
\begin{array}{c}
-0.6\\
2
\end{array}
\right],~~B=\left[
\begin{array}{c}
1\\
0.1
\end{array}
\right],\\[1mm]
& C=\left[
\begin{array}{cc}
1.2&2
\end{array}
\right],~~C_y=\left[
\begin{array}{cc}
1&-130
\end{array}
\right],~~ D=0.1,
\\[1mm]
& \alpha=0.8,~~\omega_l=0.2,~~ \omega_h=4.
\end{align*}
|
|
The eigenvalues of $A$ are $\lambda_1=-8.1842$,$\lambda_2=0.6842$,
which implies the open-loop system is unstable. Using Algorithm 2,
the initial value $U_1$ is obtained as
|
\begin{align*}
U_1=\left[
\begin{array}{cc}
-5.0654& -1.4742
\end{array}
\right],
\end{align*}
|
|
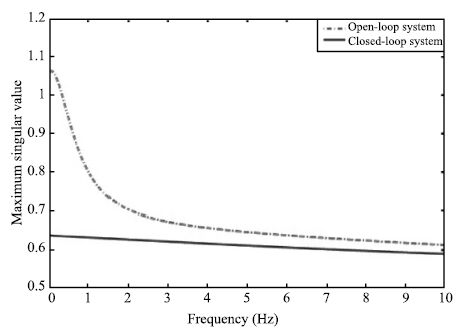
and using Algorithm 1,the desired static output feedback gain
matrix is obtained as $K=0.1370$. We can easily compute and find
that closed-loop system has the stable eigenvalues $\lambda_1$ $=
-8.7288$,$\lambda_2=-34.4677$. In addition,with the designed
controller,Fig. 1 shows the $H_\infty$ norm of the closed-loop
system is smaller than thant of open-loop system.
Example 2. Consider the system (1) with the following
parameters:
|
\begin{align*}
&A=\left[\begin{array}{cc} -2.01 & 0\\0 & -5.3\end{array}\right],\ \
B_1=\left[
\begin{array}{c}
-5\\
0.5
\end{array}
\right],\\[1mm]
& B=\left[
\begin{array}{c}
0.2\\
0.5
\end{array}
\right],\ \ C=\left[
\begin{array}{cc}
0.99&1.01
\end{array}
\right],\\[1mm]
&C_y=\left[
\begin{array}{cc}
1.01&1.89
\end{array}
\right],\ \ D=0.58,\ \ \alpha=1.2.
\end{align*}
|
|
When $w(t)=0$,it is easy to see such system is asymptotically
stable. Thus,in the following setting,we mainly make the
comparison of $H_\infty$ norm of closed loop system over different
frequency ranges. Firstly,for different frequency ranges,we adopt
same initial matrix $U=[-0.2923\ 0.1175]$ which can be obtained
by solving LMI (12). Then we can design the different
desired static output feedback controller using ILMI algorithm over
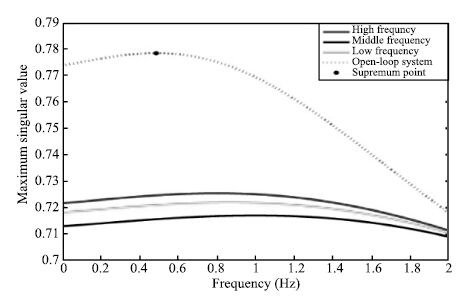
three kinds of frequency ranges. After that,the norm values of the
transfer function of the open-loop system and the closed-loop
systems over three kinds of frequency ranges,are compared in
Fig. 2,and the $H_\infty$ norm comparison are presented in Table
Ⅱ. From Fig. 2,we can see that controllers over three kinds of
frequency ranges yield the smaller $H_\infty$ norm compared with
the open loop system. From Table Ⅱ,we can see the least $H_\infty$
norm are generated by controller over the frequency range $[0.2 \
0.5]$,which exactly is the range that the supremum point of maximum
singular value of open loop system belongs to. Therefore,if the
disturbance has a finite frequency,the minimization on the entire
frequency range may not give the optimal solution. In order to
achieve a better result in the optimization,it is meaningful to
investigate the finite frequency $H_\infty$ control.
Table Ⅱ

Table Ⅱ
$H_\infty$ NORM COMPARISON OVER DIFFERENT FREQUENCY RANGES
|
Table Ⅱ
$H_\infty$ NORM COMPARISON OVER DIFFERENT FREQUENCY RANGES
|
Ⅴ. Conclusions
In this paper,the $H_\infty$ output feedback control problem of
fractional-order systems over finite frequency range has been
investigated. Based on the GKYP Lemma and the Projection Lemma,we
have established the existence conditions of the desired static
output feedback controller. By matrix congruence transformation,
the feedback gain matrix is decoupled with three matrix variables
simultaneously,and further parameterized by a scalar matrix. Two
iterative LMI algorithms have been presented to obtain the desired
results. Furthermore,the existence conditions of desired controller
have been extended to the high frequency and low frequency cases. Moreover,the design method is feasible for the fractional order
$\alpha\in(1,2)$ case. Finally,numerical examples are given to
show the effectiveness of our design method.
 2016, Vol.3
2016, Vol.3 




