2. Mechatronics Embedded Systems and Automation Lab, School of Engineering, University of California, Merced, CA 95343, USA;
3. Department of Electrical and Computer Engineering, Utah State University, Logan, UT 84322, USA
METHODOLOGY for modeling of crowds of pedestrians has been categorized as micro scale, macro scale and meso scale in previous research. It is reasonable to choose different models in different scenarios as "All models are wrong but some of them are useful" (George E. P. Box)[1]. Thus, no models are perfect for all scenarios.
A. Short Review of Mathematical Model for Crowds of PedestriansA lot of work has been done for developing microscopic model since Dirk Helbing's work of [2, 3] because the framework of social forces are similar to the framework of Newton's principle and it is not difficult to understand. Another reason for the widespread use of this social force model lies in that heterogeneity of each pedestrian such as mobilities or reactions can be considered explicitly. Thus not only theoretical work but also simulation results have gained a lot of attention such as [4, 5, 6, 7] and [8]. One thing should be pointed out is that the burden of computation in micro scale has imposed great challenges when the number of pedestrians goes to infinity and some effects such as pedestrian's memory, long range interactions or other statistical characteristics have been seldom considered in previous work. The burden of computation in microscopic model have been successfully removed in macroscopic model as all pedestrians are treated as uniform physical particles. Thus different kinds of macroscopic models have been published based on the conservation law of mass and momentum such as [9, 10, 11, 12], high order macroscopic model in [13], nonlinear macroscopic model in [14] and coupled macroscopic-microscopic model in [15]. Although the burden of computation in macroscopic model has been reduced greatly compared with that in microscopic model, main disadvantages of macroscopic model are that individual characteristics of each pedestrian have been ignored and heterogeneity of different pedestrians cannot be characterized in the macro scale.
The authors believe that something important (as mentioned below) has been neglected in previous research and its effects should be included in the problem of modeling and control of crowds so that obtained results are close to reality.
1) Consideration of fractal time
Movement of human beings is the result of complex interactions of physical part, psychological part and some other factors that cannot be explained easily. Inter-event time has been proved to have an important role in characterizing people's movement as shown in [1]. The fact is that the distribution of inter-event time in our real life satisfies one form of power law in most cases while distribution of exponential form has been always assumed in previous research using calculus of integer order. Thus fractional order of time scale should be considered in characterizing movement and decision process of human beings.
2) Consideration of fractal space
Another important thing should be pointed out is that in previous research, the time scale of each pedestrian is assumed to be uniform and the dimensions of space are restricted to 1D, 2D and 3D. But these assumptions are only reasonable if the crowds of pedestrians can fill space like particles of gases or fluids while it is not the case usually. Thus only normal diffusive process has been considered in previous research and there are few results which have been obtained under sub-diffusive process or super-diffusive process characterized by fractal space.
3) Consideration of interactions
Long range interactions have been considered in the schooling of fish, flocking of birds and control of multi-agent systems and effects of long range interactions that dominate system's phase transition have received a lot of attention recently. Based on obtained results in [16], we can say that long range interactions in micro scale are connected with the fractional dynamics in macro scale.
B. Modeling and Control Based on Mean FieldFor crowds of pedestrians with large numbers, it is impossible and not necessary to consider all the interactions one by one. In previous research, methods based on mean field have been proposed to approximate the mass effects of these interactions for physical system, financial system and social dynamic system and the readers are referred to [17, 18, 19, 20]. The basic idea of mean field framework is replacing all the interactions with an average interaction in "mean-field" form to relieve the burden of computation on each agent.
Mean field theory has been applied to control of multi-agent systems in [21, 22, 23] where decentralized consensus protocols and decentralized optimizing algorithms are considered using the philosophy of mean field. Mean field theory has also been applied to the modeling problem of crowds of pedestrians in recent years. For example, coupled dynamic model composed of backward Hamilton-Jacobi-Bellman equations and forward Fokker-Planck equations have been presented using mean-field limit approach in [20]; Phenomenons that are occurring in two-population's interactions such as congestion and aversion have been modeled using the method of mean field games in [24] where coupled dynamic model composed of backward Hamilton-Jacobi-Bellman equations and forward Fokker-Planck equations are obtained; The mean field games theory has also been used to construct traffic model in macro scale based on interactions in micro scale in [25] while fractional dynamic games have been used in [26] to construct dynamic models for crowds of pedestrians.
With the help of calculus of fractional order, in this paper we try to include the fractal time, fractal space and statistical characteristics that have been neglected in previous research on the modeling of crowds so that obtained models could be much more close to reality. Based on our previous work on fractional modeling of crowds[27, 28, 29], fractional mean field games theory has been investigated in this paper to describe the competitive and cooperative interactions among pedestrians. The rest of the paper is organized as follows. Fractional microscopic model, fractional macroscopic model and fractional dynamic model based on mean-field games are presented in Section III. Simulation results for the proposed fractional macroscopic model and fractional microscopic model have been shown in Section IV.
Ⅱ. PRELIMINARIESThe definitions of fractal derivative and lemmas that will be used in the following are firstly presented for the easy of reading.
Definition 1[30]. For a set $F\subset {\bf R}$ and a subdivision ${{P}_{[a, b]}}$, $a<b$, the mass function ${{\gamma }^{\alpha }}(F, a, b, )$ is given by
| $\gamma^{\alpha}(F, a, b)\!=\!\lim_{\delta\rightarrow0}\inf_{\{P_{[a, b]}:|P|<\delta\}}\!\!\sum_{i=0}^{n-1}\!\frac{(x_{i+1}\!-\! x_{i})^{\alpha}}{\Gamma(\alpha+1)}\theta(F, \![x_{i}, x_{i+1}]), $ |
where $\theta(F, [x_{i}, x_{i+1}])=1$ if $F\cap[x_{i}, x_{i+1}]$ is non-empty, and zero otherwise, ${{P}_{[a, b]}}$ is a subdivision of the interval $[a, b]$ and
| $|P|=\max_{0\leq i\leq n-1}(x_{i+1}-x_{i}), $ |
the infimum being taken over all subdivisions $P$ of $[a, b]$ such that $|P|<\delta$.
Definition 2[30]. Let $a_0$ be an arbitrary but fixed real number. The integral staircase function $S_{F}^{\alpha}(x)$ of order $\alpha$ for a set $F$ is given by
| $S_{F}^{\alpha}(x)=\left\{ \begin{array}{cc} \gamma^{\alpha}(F, a_{0}, x), & \quad {\rm if}\quad x\geq a_{0}, \\ -\gamma^{\alpha}(F, a, x_{0}), & \quad {\rm otherwise}. \end{array}\right.$ |
Definition 3[30]. The fractal derivative for $F^{\alpha}$-derivative of $f$ at $x$ is
| \begin{align} D_{F}^{\alpha}(f(x))=F-\lim_{y\rightarrow x}\frac{f(y)-f(x)}{S_{F}^{\alpha}(y)-S_{F}^{\alpha}(x)}, \end{align} | (1) |
if the limit exists.
From Definition 1 to Definition 3 listed above, it is easy to see that the definition of integer order can be treated as one special case of fractal derivative when $\alpha=1$. Thus the fractional calculus offers us much more freedom in modeling dynamic behaviors where ordinary differential equations and methods of calculus of integer order are inadequate.
Ⅲ. MAIN RESULTS A. Fractional Microscopic ModelThe following dynamic model of integer order has been extensively used in previous research of particles, human beings or some other agents in micro scale
| \begin{align} \left\{ \begin{alignedat}{1}\frac{{\rm d}x_{i}}{{\rm d}t} & =v_{i}, \\ m_{i}\frac{{\rm d}v_{i}}{{\rm d}t} & =f_{i}^{S}+\sum_{j=1}^{n}f_{ij}^{N}+\sum f_{k}^{W}, \end{alignedat} \right.\label{eq:micro-integer} \end{align} | (2) |
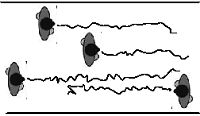
where $x_{i}$ is the position and $v_{i}$ is the velocity. One common assumption has been made that movement of each pedestrian is continuous and differentiable everywhere. That is the case if we observe the movement of each pedestrian with a very large scale such as in macro scale. However the condition of differentiable everywhere is hard to be satisfied in reality. So, will the $\frac{{\rm d}x}{{\rm d}t}$ give the true picture of pedestrian's movement in micro scale or will the $\frac{{\rm d}^{\alpha}x}{{\rm d}t^{\alpha}}$ be much closer to reality when only continuous condition is satisfied, are the questions to be explored. Related research on this fractional aspect has been shown in [31] to characterize the zigzag phenomenon that is unfolded in traffic control system. For each pedestrian, continuous but not differential trajectory is also very common due to interactions with its neighbors as shown in Fig. 1. Another fact that has been neglected in lots of previous research is that memory of human considered. This is another proof that $\frac{{\rm d}^{\alpha}x}{{\rm d}t^{\alpha}}$ is the much better choice than $\frac{{\rm d}x}{{\rm d}t}$ in characterizing the movement of each pedestrian.
|
Download:
|
| Fig. 1 Zig-zag phenomenon in movement of each pedestrian. | |
Dynamic model of integer order that was brought out by Dirk Helbing in [2, 3] has been extended to the following dynamic model of fractional order for each pedestrian
| \begin{align} \left\{ \begin{alignedat}{1}\frac{{\rm d}^{\alpha}x_{i}}{{\rm d}t^{\alpha}} & =v_{i}, \\ m_{i}\frac{{\rm d}^{\alpha}v_{i}}{{\rm d}t^{\alpha}} & =f_{i}^{S}+\sum_{j=1}^{n}f_{ij}^{N}+\sum f_{k}^{W}, \end{alignedat} \right. \end{align} | (3) |
where $x_{i}$ and $v_{i}$ are position and velocity of each pedestrian (2) respectively, $f_{i}^{S}$ is the self-driven force towards some desired velocity, $f_{ij}^{N}$ is the interaction between agent $i$ and its neighbor $j$ and $f_{k}^{W}$ represents the interactions with environment such as walls or corridors.
B. Fractional Macroscopic ModelAs fractal time and fractal space have been neglected in previous models of crowds, only macroscopic models of integer order have been obtained in previous research. Some statistical phenomenons observed in recent years have forced people to reconsider the effectiveness of obtained dynamic model of integer order.
1) Distribution of inter-event time that is dominating or affecting movement of each pedestrian can be better approximated by power law rather than exponential distribution[1]. Thus dynamic models of integer order where exponential distribution has been assumed are no longer effective when confronted with the distribution of power law. As the hidden dynamics behind distribution of power law is connected with dynamics of fractional order, it is much preferable to model crowds of pedestrians using calculus of fractional order;
2) Different from particles of gases or fluids, pedestrians do not fill the 2D or 3D space and distribution of the pedestrians is not uniform in the entire space. Thus space of integer order is not enough to describe the distribution of pedestrians and fractal space of fractional order should be included in modeling of crowds of pedestrians.
Based on [9] where modeling of traffic system has been considered using calculus of integer order, we try to model crowds of pedestrians using calculus of fractional order in the following.
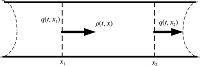
Denote $\rho(x, t)$ as the density of crowds as shown in Fig. 2, then mass of pedestrians between $x=x_{1}$ to $x=x_{2}$ at time $t$ can be computed as
|
Download:
|
| Fig. 2 Conservation of mass. | |
| \begin{align} \mbox{mass in}[x_{1}, x_{2}]\mbox{ at time}\, t\, :=\int_{x_{1}}^{x_{2}}\rho(x, t){\rm d}x^{\beta}. \end{align} | (4) |
For $t\in[t_{1}, t_{2}], $ the total mass that enters this domain from the left boundary at $x=x_{1}$ is given by
| \begin{align} \mbox{inflow at}\ x_{1}\ \mbox{from}\ t_{1}\ \mbox{to}\ t_{2}\, :=\!\!\int_{t_{1}}^{t_{2}}\rho(x_{1}, t)v(t, x_{1}){\rm d}t^{\alpha} \end{align} | (5) |
Similarly, the total mass that leaves this domain from the right boundary at $x=x_{2}$ for $t\in[t_{1}, t_{2}]$ is given by
| \begin{align} \mbox{outflow at}\ x_{2}\ \mbox{from}\ t_{1}\ \mbox{to}\ t_{2}\, :=\!\!\!\int_{t_{1}}^{t_{2}}\!\!\!\rho(x_{2}, t)v(t, x_{2}){\rm d}t^{\alpha} \end{align} | (6) |
The change of people in the area between $x_{1}$ and $x_{2}$ is caused by crossing of people at the boundary of $x_{1}$ and $x_{2}$. Assuming no pedestrians are created or destroyed, then the change of mass of pedestrians in space $[x_{1}, x_{2}]$ in time interval $[t_{1}, t_{2}]$ is equal to the mass that is entering at $x_{1}$ minus that exiting from $x_{2}$. This conservation can be described using
| \begin{align*} &\int_{x_{1}}^{x_{2}}\!\!\!\!\rho(x, t_{2}){\rm d}x^{\beta} \!\!-\!\!\int_{x_{1}}^{x_{2}}\!\!\!\!\rho(x, t_{1}){\rm d}x^{\beta}\\ &\quad =\int_{t_{1}}^{t_{2}}\!\!\!\!\rho(x_{1}, t)v(t, x_{1})dt^{\alpha}\!\!-\!\!\int_{t_{1}}^{t_{2}}\!\!\!\!\rho(x_{2}, t)v(t, x_{2}){\rm d}t^{\alpha}. \end{align*} |
The above equation can also be written as the following double integral form
| \begin{align} \int_{x_{1}}^{x_{2}}\int_{t_{1}}^{t_{2}}\left\{\frac{\partial}{\partial t^{\alpha}}\rho(x, t)+\frac{\partial}{\partial x^{\beta}}[\rho(x, t)v(t, x)]\right\}{\rm d}t^{\alpha}{\rm d}x^{\beta}=0.\label{double} \end{align} | (7) |
| $\frac{\partial }{\partial {{t}^{\alpha }}}\rho (x, t)+\frac{\partial }{\partial {{x}^{\beta }}}[\rho (x, t)v(t, x)]=0, $ | (8) |
can be derived where fractal time and fractal space have been included in (8).
Remark 1. Part of the results of fractional model in macro scale has been firstly brought out in [27] and is listed here to guarantee the completeness.
Remark 2. Similar results are also obtained in [32] where fractional model for traffic flow has been derived using fractional conservation law. Different from the work of [32] where dimension of time is $\alpha$, dimension of surface is $2\alpha$ and dimension of volume is $3\alpha$, there are no such restrictions in our fractional model (8).
C. Fractional Micro-macro Model1) Fractional Hamilton-Jacobi-Bellman Equation
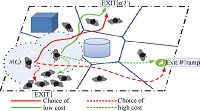
For each pedestrian $i$, we assume the following cost function to be minimized in his/her movement between initial starting point $x(t_{0})=x_{0}$ and desired location $x(T)$ as shown in Fig. 3.
|
Download:
|
| Fig. 3 Movement of pedestrians based on fractional mean field games. | |
| \begin{align} J(t_{0}, x_{0})=\underset{v(\cdot)}{inf}\int_{t_{0}}^{T}f(t, x(t), v(t)){\rm d}t^{\alpha}+h(T, x(T)), \end{align} | (9) |
where convex function $h(T, x(T))$ is the terminal cost, convex even function $f(t, x(t), v(t))$ describes some different kinds of running cost between the initial point and destination.
Remark 3. A typical quadratic cost function that is independent of position of pedestrians' can be selected as $\frac{1}{2}|v|^{2}$ to penalize pedestrians that are moving too fast; Much more generalized running cost functions that depend on time, position and velocity have been adopted in the following derivation of fractional Hamilton-Jacobi-Bellman equation.
Similar to the derivation of Hamilton-Jacobi-Bellman equation of integer order in optimal control, the fractional Hamilton-Jacobi-Bellman equation will be discussed firstly and then optimal velocity will be prescribed for each pedestrian at each time step. Suppose after an infinitesimal time interval ${\rm d}t^{\alpha}$, the pedestrian will arrive at one new place $x_{0}+v{\rm d}t^{\alpha}$ and thus incurring a travel cost of $f(v){\rm d}t^{\alpha}$ where new cost function for the remaining journey is described by $J(t_{0}+{\rm d}t^{\alpha}, x_{0}+v{\rm d}t^{\alpha})$. The above analysis leads to the following relationship between $J(t_{0}, x_{0})$ and $J(t_{0}+{\rm d}t^{\alpha}, x_{0}+v{\rm d}t^{\alpha})$
| \begin{align} J(t_{0}, x_{0})=J(t_{0}+{\rm d}t^{\alpha}, x_{0}+v{\rm d}t^{\alpha})+f(v){\rm d}t^{\alpha}. \end{align} | (10) |
Based on Taylor expansion, Equation (10) can be rewritten as
| \begin{align} \begin{aligned}J(t_{0}, x_{0})&=J(t_{0}, x_{0}) +dt^{\alpha}[\frac{\partial^{\alpha}}{\partial t^{\alpha}}J(t_{0}, x_{0})\\ & +v\cdot\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0})+f(v)], \end{aligned} \label{eq:Taylor} \end{align} | (11) |
and the optimal problem (9) is now transformed into finding proper $v$ to minimize
| $v\cdot\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0})+f(v).$ |
Considering the fact that $f(\cdot)$ is an even function, the above minimization problem is equivalent to the maximization problem of
| \begin{align} v\cdot\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0})-f(v).\label{eq:maxmum problem} \end{align} | (12) |
Based on the Legendre transformation $H:R^{d}\rightarrow R$ of $f:R^{d}\rightarrow R$ by
| \begin{align} H(p)~\text{:=}~\underset{v(\cdot)}{sup}\, v\cdot p-f(v)\label{eq:Legendre} \end{align} | (13) |
whose maximum value are functions of $p$. For the maximization problem of (12), we can see that the maximum value is obtained as $H(\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0})$) for some $v$. Then substituting the minimum value $-H(\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0}))$ into (11), the following equation
| $J(t_{0}, x_{0})=J(t_{0}, x_{0})+{\rm d}t^{\alpha}[\frac{\partial^{\alpha}}{\partial t^{\alpha}}J(t_{0}, x_{0})-H(\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0}))]$ |
will be satisfied for any $t_{0}$ and any $x_{0}.$ Then the fractional Hamilton-Jacobi-Bellman equation is derived as
| \begin{align} -\frac{\partial^{\alpha}}{\partial t^{\alpha}}J(t_{0}, x_{0})+H(\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0}))=0.\label{eq:fraction HJB} \end{align} | (14) |
From the above discussions, we know that there is one $v$ that minimize the following expression
| $v\cdot\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0})+f(v), $ |
and $\widetilde{v}=-v$ maximize the following expression
| $v\cdot\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0})-f(v).$ |
As seen from (13), $\widetilde{v}$ as a function of $p$ should satisfy that
| $\frac{\partial}{\partial\widetilde{v}}(\widetilde{v}\cdot p-f(\widetilde{v}))=0.$ |
On the other hand, the derivative of $H(p)$ can be obtained as follows
| $\frac{d}{dp}H(p)=\frac{\partial H}{\partial\widetilde{v}}\frac{\partial\widetilde{v}}{\partial p}+\frac{\partial H}{\partial p}=\widetilde{v}, $ |
using chain rule and then the velocity for each pedestrian to move in the next step is derived as
| $v=-H^{\prime}(\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0})).$ |
2) Fractional Macro Model Based on Fractional Mean Field Games
Based on inspiration of [25] on traffic system, we assume the following utility function for the $i$-{th} pedestrian
| $f_{i}^{N}(x_{i}, v_{i})=v_{i}(1-F(\frac{1}{N}\sum\omega(x_{j}-x_{i}))), $ |
where the first term $v_{i}$ means that the $i-\text{th}$ pedestrian tries to arrive his destination as fast as possible; the second term means that the $i-\text{th}$ pedestrian adapts his velocity according to pedestrians around him. Bounded non-negative anticipating function $\omega(\cdot)$ has been introduced to weigh different impacts of pedestrians in the neighborhood of the $i-\text{th}$ pedestrian according to their distances. Thus for the $i-\text{th}$ pedestrian, cooperative and competitive interacting with other pedestrians are manifested through choosing velocity in the next step.
First, we show that the following expression is satisfied
| $\lim_{N\rightarrow\infty}\frac{1}{N}\sum\omega(x_{j}-x_{i})\rightarrow\int_{0}^{\infty}\rho_{t}(y)\omega(y-x){\rm d}y^{\beta}, $ |
where $N$ is the number of interacting pedestrians, $\rho_{t}(y)$ is the number of pedestrians in interval $[x, x+dx^{\beta}]$ and $\omega(\cdot)$ is the anticipating function mentioned above.
Denote $\varGamma_{t}^{N}(x)=\frac{1}{N}\sum1_{\{x_{j}<x\}}$ as the empirical distribution function for the crowds composed of $N$ pedestrians. Then based on the Lebesgue-Stieltjes integral it can be concluded that
| $\frac{1}{N}\sum\omega(x_{j}-x_{i})=\int_{0}^{\infty}\omega(y-x){\rm d}\varGamma_{t}^{N}(y).$ |
If there is one non-decreasing right-continuous function $\varGamma_{t}(x)$ such that the following expression is satisfied
| $\int_{0}^{\infty}\omega(y-x){\rm d}\varGamma_{t}^{N}(y)\rightarrow\int_{0}^{\infty}\omega(y-x){\rm d}\varGamma_{t}(y)(N\rightarrow\infty).$ |
Then
| $\frac{1}{N}\sum\omega(x_{j}-x_{i})\rightarrow\int_{0}^{\infty}\rho_{t}(y)\omega(y-x){\rm d}y^{\beta}(N\rightarrow\infty)$ |
will be satisfied. As $\rho_{t}(y)$ is the number of pedestrians in interval $[x, x+{\rm d}x^{\beta}]$, existence of non-decreasing right-continuous function $\varGamma_{t}(x)$ can be guaranteed from ${\rm d}\varGamma_{t}(x)=\rho_{t}(x){\rm d}x^{\beta}.$ Thus we can impose the following mean field payoff function
| $\begin{aligned}J(t_{0}, x_{0}, \rho_{t}(x))&= \underset{v(\cdot)}{sup}\int_{t_{0}}^{T}\!\! v(1\!-\! F(\int_{0}^{\infty}\!\!\rho_{t}(y)\omega(y-x){\rm d}y^{\beta})){\rm d}t^{\alpha}\\ & +h(T, x(T)) \end{aligned}$ |
for pedestrians that are competitively and cooperatively interacting with other pedestrians.
Based on similar derivations shown in Section III-C-1, the following fractional Hamilton-Jacobi-Bellman equation
| $-\frac{\partial^{\alpha}}{\partial t^{\alpha}}J(t_{0}, x_{0})+H(\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0}, \rho_{t}(x)))=0$ |
can also be obtained for modeling cooperative and competitive crowds using mean field game theory when the number of pedestrians goes to infinity.
Remark 4. Differences from previous work are listed as following:
a) Only functions of Dirac type and exponential type for $\omega(x_{j}-x_{i})$ have been considered in [25]. Anticipating function of inverse power form
| $f_{i}^{N}(x_{i}, v_{i})=v_{i}[1-F(\frac{1}{N}\sum(\left|x_{j}-x_{i}\right|+1){}^{-2})]$ |
can be included in this paper considering the long range effects in interacting of multiple pedestrians, where $\frac{1}{N}$ has been introduced to normalize the effects of other pedestrians on the $i$-{th} pedestrian.
b) Mean field games theory is also utilized in [20] for modeling crowds of pedestrians. But obtained results of [20] are only restricted to the framework of calculus of integer order and many statistical characteristics are not considered such as power law in distribution of crowds, power law in distribution of inter-event time and long range interactions among pedestrians.
3) Fractional Micro-macro Model
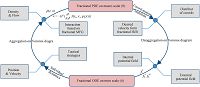
As shown in Fig. 4, the fractional micro-macro model for crowds of pedestrians using fractional mean field games can be described as the following backward-forward PDE systems
|
Download:
|
| Fig. 4 Fractional micro-macro model of crowds of pedestrians. | |
| $\left\{ \begin{array}{*{35}{l}} -\frac{{{\partial }^{\alpha }}}{\partial {{t}^{\alpha }}}J({{t}_{0}}, {{x}_{0}}, {{\rho }_{t}}(x))+H(\frac{{{\partial }^{\beta }}}{\partial {{x}^{\beta }}}J({{t}_{0}}, {{x}_{0}}, {{\rho }_{t}}(x)))=0, \\ n\frac{\partial }{\partial {{t}^{\alpha }}}\rho (t, x)+\frac{\partial }{\partial {{x}^{\beta }}}[\rho (t, x)v(t, x)]=0, \\ \end{array} \right.$ | (15) |
and
| \begin{align} \left\{ \begin{alignedat}{1}\frac{{\rm d}^{\alpha}x_{i}}{{\rm d}t^{\alpha}} & =v_{i}, \\ m_{i}\frac{{\rm d}^{\alpha}v_{i}}{{\rm d}t^{\alpha}} & =f_{i}^{S}+\sum_{j=1}^{n}f_{ij}^{N}+\sum f_{k}^{W}. \end{alignedat} \right. \end{align} | (16) |
The fractional microscopic model and fractional macroscopic model are connected through aggregation and disaggregation on Voronoi Diagram. From Fig. 4, the following can be observed.
1) Movements of each microscopic model are determined by not only internal potential fields such as the self-driven force towards some desired velocity described using $f_{i}^{S}$ in (16) but also external interactions from neighbors and environments which are described using $f_{ij}^{N}$ and $f_{k}^{W}$. Some other elements such as deviations from optimal movement of the whole crowds are also playing an important role in the movement of each individual pedestrian. All these information are generated from the dynamic model in macro scale;
2) Density and velocity that are needed in macroscopic model are derived from aggregation of individual's position and velocity. When the number of pedestrians goes to infinity, the crowds of pedestrians are treated as some intelligent flows that are described with the help of fractional MFG as shown in (15). For the backward part, $v$ can be solved from the first line of (15) under initial condition on $J(T, X_{T})$ and initial distribution of $\rho_{0}(x)$; Then substitute the obtained $v$:
| $v=-H^{\prime}(\frac{\partial^{\beta}}{\partial x^{\beta}}J(t_{0}, x_{0}, \rho_{t}(x)))$ |
into the forward part and $\rho(t, x)$ will be obtained from the second line of equation (15) under initial condition $\rho_{0}(x)$.
Due to the complexity of crowds of pedestrians, fractional microscopic model and fractional macroscopic model that interacted with each other have been constructed in this paper. Fractional mean field games have also been utilized in describing the macroscopic model when the number of pedestrians goes to infinity.
Remark 5. To the author's knowledge, the paper is one of the first works applying fractional mean field games to fractional macroscopic and microscopic model for competitive and cooperative crowds of pedestrians. Although some theoretical results have been obtained, a lot of work is waiting for further efforts such as existence and uniqueness of solution, rate of convergence and stability of desired equilibrium.
Ⅳ. SIMULATION RESULTSConsidering unexpected or dangerous events in real-life experiment, only some initial simulation results are conducted to show the differences between model of fractional order and model of integer order in macro scale and micro scale. Due to the difficulties caused when the number of pedestrians goes to infinity, simulation results in macro scale and micro scale are separated in the following subsections. All we want to show is that calculus of fractional order has offered us much more freedom in describing complex phenomenon or dynamics such as crowds of pedestrians. It is much preferable to choose different model according to different scenarios and there are a lot of interesting problems needing to be considered in future.
A. Fractional Macroscopic Model1) Simulation in Closed and Square Area Without Exit: Simulations on fractional macroscopic model (8) are firstly conducted where $\beta=1$ is imposed for simplicity. Lax-Friedrichs scheme has been used to approximate the spatial derivatives in solving the nonlinear partial differential equations due to its efficiency in computation. Based on Lax-Friedrichs scheme, the following PDE on 2D plane
| \[\begin{align} & \frac{\partial }{\partial {{t}^{\alpha }}}\rho (t, x, y)+\frac{\partial }{\partial x}[\rho (t, x, y)v(t, x, y)] \\ & +\frac{\partial }{\partial y}[\rho (t, x, y)v(t, x, y)]=0, \\ \end{align}\] |
has been transformed into
| \[\begin{align} & \frac{\partial }{\partial {{t}^{\alpha }}}\rho (t, x, y)+\frac{1}{2Dx}[\rho (t, x+1, y)v(t, x+1, y) \\ & -\rho (t, x-1, y)v(t, x-1, y)]+\frac{1}{2Dy}[\rho (t, x, y+1)v(t, x, y+1) \\ & -\rho (t, x, y-1)v(t, x, y-1)]=0 \\ \end{align}\] |
in this simulation and the following Gaussian distribution
| $\rho(x, y, 0)=C\exp(-(x-a)^{2}-(y-b)^{2}), $ |
has been selected as the initial distribution of density where $C=1$ is the density value and $(a, b)$ determines the center of this initial distribution. Average speed of free flow has been chosen to be $v_{x}=v_{y}=1.36\, {\rm ms}^{-1}$as done in many previous studies for pedestrians. Pedestrians have also been assumed to move freely within a square area with no obstacles and no exits in the first simulations.
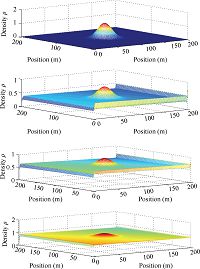
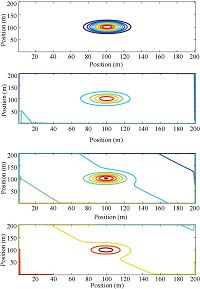
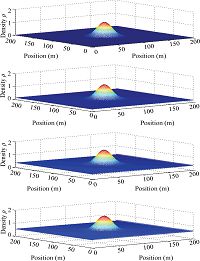
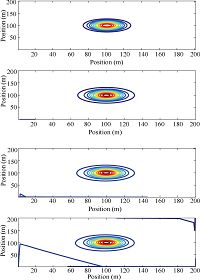
Simulation results for $\alpha=0.6$ and $\alpha=1$ are shown in Fig. 5-6 and Figs.7-8, respectively. From Fig. 5 and Fig. 7-8, it can be concluded that pedestrians described using fractional model are much scattered in the closed square area than that described using model of integer order. Same conclusions can also be obtained from comparisons of Fig. 6 and Fig. 8. Other fractional orders can also be tested using the methods proposed in this paper but data from reality are much preferable to find the proper orders for modeling the crowds of pedestrians in macro scale.
|
Download:
|
| Fig. 5 Density response for crowds of pedestrians with $\alpha=0.6$ using Lax-Friedrichs scheme. | |
|
Download:
|
| Fig. 6 Contour of the density response for crowds of pedestrians with $\alpha=0.6$ using Lax-Friedrichs scheme. | |
|
Download:
|
| Fig. 7 Density response for crowds of pedestrians of integer order using Lax-Friedrichs scheme. | |
|
Download:
|
| Fig. 8 Contour of the density response for crowds of pedestrians of integer order using Lax-Friedrichs scheme. | |
2) Simulation in Closed and Square Area with one Exit
Based on results obtained in Section IV-A-1, the following dynamic model has been simulated for pedestrians in closed and square area with one exit
| $\left\{ \begin{array}{*{35}{l}} \frac{\partial }{\partial {{t}^{\alpha }}}\rho (t, x, y)+\frac{\partial }{\partial x}[\rho (t, x, y)v(t, x, y)] \\ +\frac{\partial }{\partial y}[\rho (t, x, y)v(t, x, y)]=0, \\ {{v}_{t}}+v{{v}_{x}}=\frac{V-v}{\tau }-\frac{C_{0}^{2}}{\rho }{{\rho }_{x}}, \\ {{u}_{t}}+u{{u}_{y}}=\frac{U-u}{\tau }-\frac{C_{0}^{2}}{\rho }{{\rho }_{y}}, \\ \end{array} \right.$ |
where $C_{0}=0.8$ is the anticipation term that describes the response of pedestrians to density of people and $V$ and $U$ are some desired velocity that are obtained for the crowds. In order to lead the crowd moving toward the exit, the desired velocity $V$ and $U$ are selected as done in [33]
| $\left\{ \begin{array}{cc} V= & V(\rho)\frac{x_{e}-x_{i}}{\sqrt{(x_{e}-x_{i})^{2}+(y_{e}-y_{i})^{2}}}, \\ U= & U(\rho)\frac{y_{e}-y_{i}}{\sqrt{(x_{e}-x_{i})^{2}+(y_{e}-y_{i})^{2}}}, \end{array}\right.$ |
where $V(\rho)$ and $U(\rho)$ are the flux-density relationship for Greenshield's model.
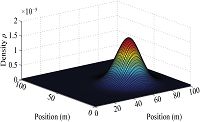
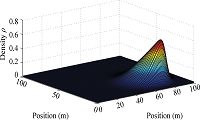
Simulation results are shown in Fig. 9-10 where dynamic model with fractional orders $0.85$ and $1$ are used. Simulation results show that the density of pedestrians around the exit is much lower in model of fractional order than that obtained using model of integer order. In simulations, the authors found that the final density of pedestrians is depending on the fractional order selected in the simulation and how to choose the best order to model the dynamics of crowds is an interesting problem that is worthy of further consideration in future research.
|
Download:
|
| Fig. 9 Density response for crowds of pedestrians with $\alpha=0.85$ using Lax-Friedrichs scheme. | |
|
Download:
|
| Fig. 10 Contour of the density response for crowds of pedestrians with $\alpha=1$ using Lax-Friedrichs scheme. | |
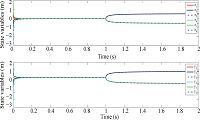
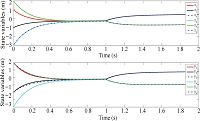
In this section, six pedestrians with fractional order $\alpha\in(0, 1)$, $\alpha=1$ and $\alpha\in(1, 2)$ are employed respectively to show their effects on pedestrian's evacuation process. Simulations of crowds of pedestrians with fractional order $\alpha=0.6$, $\alpha=1$ and $\alpha=1.3$ are shown in Fig. 11-13 respectively. Results show that all agents firstly reach consensus through interacting with their neighbors without games. But parts of them change their desired value and fragmentation phenomenon are observed through these simulations after some penalty terms are injected into the simulations. Obtained simulation results have shown that pedestrians with different orders have different performance. Thus fractional calculus has provided us much more freedom in analysis and control of this kind of complex system. How to quantitatively characterize the relationship between order of fractional model, fractional controller and fractional games are interesting topics to be considered by the authors.
|
Download:
|
| Fig. 11 Responses of six pedestrians with $\alpha=0.6$. | |
|
Download:
|
| Fig. 12 Responses of six pedestrians with $\alpha=1$. | |
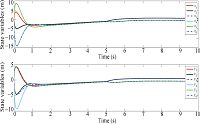
|
Download:
|
| Fig. 13 Responses of six pedestrians with $\alpha=1.3$. | |
Modeling of crowds of pedestrians have been considered in this paper from the view of fractional calculus. Not only fractional microscopic models but also fractional macroscopic models have been proposed in this paper. Fractional mean field games theory has been introduced in the modeling of crowds of pedestrians and coupled PDEs composed of fractional backward part and fractional forward part have been investigated. Although some theoretical results and some initial simulations are presented in this paper, there is much more work unexplored along this topic, such as solution of fractal MFG systems, stability of the fractal MFG system and performance of this fractal system, controller design based on mean field, performance evaluation of dynamic crowds and security problems related to control of crowds.
| [1] | West B J, Turalska M, Grigolini P. Networks of Echoes: Imitation, Innovation and Invisible Leaders. Switzerland: Springer International Publishing, 2014. |
| [2] | Helbing D, Molnar P. Social force model for pedestrian dynamics. Physical Review E, 1995, 51(5): 4282-4286 |
| [3] | Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic. Nature, 2000, 407(6803): 487-490 |
| [4] | Bellomo N, Bianca C, Coscia V. On the modeling of crowd dynamics: an overview and research perspectives. SeMA Journal, 2011, 54(1): 25-46 |
| [5] | Couzin I D, Krause J, Franks N R, Levin S A. Effective leadership and decision-making in animal groups on the move. Nature, 2005, 433(7025): 513-516 |
| [6] | Couzin I D. Collective cognition in animal groups. Trends in Cognitive Sciences, 2009, 13(1): 36-43 |
| [7] | Song W G, Xu X, Wang B H, Ni S J. Simulation of evacuation processes using a multi-grid model for pedestrian dynamics. Physica A, 2006, 363(2): 492-500 |
| [8] | Shiwakoti N, Sarvi M, Rose G, Burd M. Animal dynamics based approach for modeling pedestrian crowd egress under panic conditions. Transportation Research, Part B: Methodological, 2011, 45(9): 1433-1449 |
| [9] | Kachroo P. Pedestrian Dynamics: Mathematical Theory and Evacuation Control. Boca Raton: CRC Press, 2009. |
| [10] | Helbing D. A fluid dynamic model for the movement of pedestrians. Complex Systems, 1992, 6: 391-415 |
| [11] | Hughes R L. A continuum theory for the flow of pedestrians. Transportation Research, Part B: Methodological, 2002, 36(6): 507-535 |
| [12] | Hughes R L. The flow of human crowds. Annual Review of Fluid Mechanics, 2003, 35: 169-182 |
| [13] | Jiang Y Q, Zhang P, Wong S C, Liu R X. A higher-order macroscopic model for pedestrian flows. Physica A: Statistical Mechanics and its Applications, 2010, 389(21): 4623-4635 |
| [14] | Al-nasur S J. New Models for Crowd Dynamics and Control [Ph. D. dissertation], Virginia Polytechnic Institute and State University, Virginia, 2006. |
| [15] | Lattanzio C, Maurizi A, Piccoli B. Moving bottlenecks in car traffic flow: a PDE-ODE coupled model. SIAM Journal on Mathematical Analysis, 2011, 43(1): 50-67 |
| [16] | Ishiwata R, Sugiyama Y. Relationships between power-law longrange interactions and fractional mechanics. Physica A, 2012, 391(23): 5827-5838 |
| [17] | Achdou Y, Camilli F, Capuzzo-Dolcetta I. Mean field games: numerical methods for the planning problem. SIAM Journal on Control and Optimization, 2012, 50(1): 77-109 |
| [18] | Caines P E. Mean field stochastic control. In: Proceedings of the 48th Conference on Decision and Control and the 28th Chinese Control Conference. Shanghai, China: IEEE, 2009. |
| [19] | Gueant. A reference case for mean field games models. Journal de Mathematiques Pures et Appliquees, 2009, 92(3): 276-294 |
| [20] | Dogbe C. Modeling crowd dynamics by the mean-field limit approach. Mathematical and Computer Modelling, 2010, 52(9-10): 1506-1520 |
| [21] | Nourian M, Malhame R P, Huang M Y, Caines P E. Mean field (NCE) formulation of estimation based leader-follower collective dynamics. International Journal of Robotics & Automation, 2011, 26(1): 120-129 |
| [22] | Nourian M, Caines P E, Malhame R P, Huang M Y. Mean field LQG control in leader-follower stochastic multi-agent systems: likelihood ratio based adaptation. IEEE Transactions on Automatic Control, 2012, 57(11): 2801-2816 |
| [23] | Nourian M, Caines P E, Malhame R P, Huang M Y. Nash, social and centralized solutions to consensus problems via mean field control theory. IEEE Transactions on Automatic Control, 2013, 58(3): 639-653 |
| [24] | Lachapelle A, Wolfram M T. On a mean field game approach modeling congestion and aversion in pedestrian crowds. Transportation Research, Part B: Methodological, 2011, 45(10): 1572-1589 |
| [25] | Chevalier G, Le Ny J, Malhame R. A micro-macro traffic model based on mean-field games. In: Proceedings of the 2015 American Control Conference. Chicago, IL, USA: IEEE, 2015. 1983-1988 |
| [26] | Bogdan P, Marculescu R. A fractional calculus approach to modeling fractal dynamic games. In: Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference. Orlando, FL: IEEE, 2011. 255-260 |
| [27] | Cao K C, Zeng C B, Stuart D, Chen Y Q. Fractional order dynamic modeling of crowd pedestrians. In: Proceedings of the 5th Symposium on Fractional Differentiation and its Applications. 2012. |
| [28] | Cao K C, Chen Z Q, Stuart D, Yue D. Cyber-physical modeling and control of crowd of pedestrians: a review and new framework. IEEE/CAA Journal of Automatica Sinica, 2015, 2(3): 334-344 |
| [29] | Cao K C, Chen Y Q, Stuart D. A new fractional order dynamic model for human crowd stampede system. In: Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Boston, USA: ASME, 2015. |
| [30] | Parvate A, Gangal A D. Fractal differential equations and fractal-time dynamical systems. Pramana, 2005, 64(3): 389-409 |
| [31] | Das S. Functional Fractional Calculus. Berlin Heidelberg: Springer-Verlag, 2011. |
| [32] | Wang L F, Yang X J, Baleanu D, Cattani C, Zhao Y. Fractal dynamical model of vehicular traffic flow within the local fractional conservation laws. Abstract and Applied Analysis, 2014, 2014(2014): Article ID 635760 |
| [33] | Kachroo P, Al-Nasur S J, Wadoo S A, Shende A. Pedestrian Dynamics: Feedback Control of Crowd Evacuation. Berlin Heidelberg: Springer-Verlag, 2008. |
 2016, Vol.3
2016, Vol.3 


