Reliability of the repairable system has been widely investigated by scholars in the past few decades. Some results were summarized in ^[1]. Repairable systems were further studied by introducing the Ion-Channel modeling theory into biological pharmacology^[2]. Zheng et al.^[3] discussed a single-unit Markov repairable system with repair time omission by using aggregated stochastic process theory for the first time. The availabilities of the original system and the new system were obtained in the paper,respectively. Cui et al.^[4] modeled Markov repairable systems with history-dependent up and down states,among which some states are changeable in the sense that whether those physical states are up and down depends on the immediately preceding state of the system evolution process. Wang and Cui^[5] extended the model into the semi-Markov repairable system with history-dependent up and down states which is more realistic than the previous one. A Markov system with stochastic supply patterns and stochastic demand patterns was investigated by Liu et al.^[6],and several performance measures of the system were also proposed. Many works have been done on the research of the Markov repairable model using aggregated stochastic theory,see ^{[7,8,9,10,11,12]}. Reliability and availability are two important reliability indexes in traditional reliability field. They can be used to describe various properties of the repairable system very well. However,some situations could not be covered by these indexes yet,so that Cui et al.^[11] defined several new reliability indexes of repairable systems,such as multiple-point availability, multiple-intervals reliability,mixed multi-point-interval availabilities and so on.

The environment condition in which the system operates influences the performance of the system,so that the environment cannot be ignored when we evaluate the system performance. For example, systems under very high strength fail mainly due to temperature, voltage or vibrations; motors can fail under vibrations of high intensity,or other environments. Therefore,shock models were studied extensively in the past decades. Markov arrival process (MAP) is an important point process,and it has been widely applied in the field of queuing theory. Recently,MAP has been used for modeling the shock arrival in the reliability domain by several Spain scholars,such as ^[13,14,15],etc. Hawkes et al. said that systems may operate in different environments,such as a machine operating in days and nights,stock markets being a bull market or a bear market,tourist markets in different seasons,a system operating in degradation and recovery,economic situation in recession and boom,a country governed alternately by two political parties^[9]. However,in the reliability field,to our best knowledge,there are only few existing works on the Markov switching model. Lim^[16] considered a switching of the regimes governing the lifetime distribution of the system. Ravishanker et al.^[17] constructed non-homogenous Poisson process (NHPP) model with Markov switching for software reliability. Hawkes et al.^[9] studied the reliability of the system operating in alternative environments. Markov repairable systems with two stochastic regimes switching were investigated in ^[10]. A single-unit system which operates in a Markovian environment was investigated in ^[18] and the failure time distribution was derived. Kharoufeh et al.^[19] studied the reliability of manufacturing equipment in complex environments, where the environment was assumed to be a temporally non-homogeneous continuous-time Markov chain and a temporally homogeneous semi-Markov process,respectively. The lifetime distribution was obtained in that paper.

However,in these papers the system operated only in two environments or two regimes switching. Reliability indexes of the system operating in complex environments were very poor. This motives us to study the reliability of systems under multiple environments. Our model is motivated by Cekyay and $\ddot{O}$zekici^[20] who considered a mission-based reliability system where the missions consist of a random sequence of phases or stages with random durations. In our setting,this mission process is the environment process. The novelty with respect to previous papers is introducing of multiple environments,and the system is studied using aggregated stochastic process theory that is borrowed from the Ion-Channel modeling theory

The rest of paper is organized as follows. In Section Ⅱ,the system is presented and the Markov process governing the system is constructed. In Section Ⅲ,the system reliability and the environment reliability are derived,respectively. The system availability and the environment availability are given, respectively in Section Ⅳ. In Section Ⅴ,a numerical application is performed. Concluding remarks are offered in the last section.

We assume that the system operates in multiple environments. The environment process $\{X(t):t\ge 0\}$ is a Markov process with a finite state space $E=\{e_1 ,e_2 ,... ,e_m \}$,transition rate matrix ${{H}}$,and the initial probability vector ${\rm {\bf \alpha }}=$ $( 1,0,... ,0)_{1\times m} $. The deterioration process of the system is denoted by $\{Y(t):t\ge 0\}$. Its finite state space is denoted by $S=\{1,2,... ,n\}$,where some states are changeable,i.e.,they may be open in some environments,closed in others environments. When the system operates in $e_i\in E$,the state space of the system can be partitioned as $S=\{1,$ $...,$ $n_i \}\cup \{n_i +1,... ,n\}=W_i \cup F_i $,where $W_i $ and $F_i $ denote working states and failure states,respectively. The infinitesimal generator of $\{Y(t):t\ge 0\}$ in the environment $e_i $ is ${{G}}_i $.

Let $Z(t)=\left( {X(t),Y(t)} \right)$,then the combined,bivariate stochastic process $\{Z(t),t\ge 0\}$ models the interaction between environment and deterioration. Its state space is $E\times S$,the Cartesian product of the individual state spaces $E$ and $S$. Because of independence of the component processes,$\{Z(t),$ $t \ge 0\}$ is a Markov process with transition rate matrix ${ { G}}=$ $( G(i,a;j,b))$,where $G(i,a;j,b)=\left\{ \begin{array}{*{35}{l}} {{G}_{i}}(a,b),& \text{if}~i=j,a\ne b,\\ H(i,j),& \text{if}~i\ne j,a=b,\\ {{G}_{i}}(a,a)+H(i,i),& \text{if}~i=j,a=b,\\ 0,& \text{otherwise,} \\ \end{array} \right.$ for every $i,j\in {{E}}$,and $a,b\in {{S}}$. The initial probability vector of $\{Z(t),t\ge 0\}$ is ${\rm {\bf \gamma }}=\left( {1,0,... ,0} \right)_{1\times mn} $.

Based on the partition of the state space ${{S}}$,the transition rate matrix ${{G}}$ can be partitioned as $\begin{gathered} G = \hfill \\ \left( {\begin{array}{*{20}{c}} {{G_{{W_1}{W_1}}}}&{{G_{{W_1}{F_1}}}}&{{G_{{W_1}{W_2}}}}&{{G_{{W_1}{F_2}}}}& \cdots &{{G_{{W_1}{W_m}}}}&{{G_{{W_1}{F_m}}}} \\ {{G_{{F_1}{W_1}}}}&{{G_{{F_1}{F_1}}}}&{{G_{{F_1}{W_2}}}}&{{G_{{F_1}{F_2}}}}& \cdots &{{G_{{F_1}{W_m}}}}&{{G_{{F_1}{F_m}}}} \\ {{G_{{W_2}{W_1}}}}&{{G_{{W_2}{F_1}}}}&{{G_{{W_2}{W_2}}}}&{{G_{{W_2}{F_2}}}}& \cdots &{{G_{{W_2}{W_m}}}}&{{G_{{W_2}{F_m}}}} \\ {{G_{{F_2}{W_1}}}}&{{G_{{F_2}{F_1}}}}&{{G_{{F_2}{W_2}}}}&{{G_{{F_2}{F_2}}}}& \cdots &{{G_{{F_2}{W_m}}}}&{{G_{{F_2}{F_m}}}} \\ {\quad \vdots }&{\quad \vdots }&{\quad \vdots }&{\quad \vdots }&{\; \vdots }&{\quad \vdots }&{\quad \vdots } \\ {{G_{{W_m}{W_1}}}}&{{G_{{W_m}{F_1}}}}&{{G_{{W_m}{W_2}}}}&{{G_{{W_m}{F_2}}}}& \cdots &{{G_{{W_m}{W_m}}}}&{{G_{{W_m}{F_m}}}} \\ {{G_{{F_m}{W_1}}}}&{{G_{{F_m}{F_1}}}}&{{G_{{F_m}{W_2}}}}&{{G_{{F_m}{F_2}}}}& \cdots &{{G_{{F_m}{W_m}}}}&{{G_{{F_m}{F_m}}}} \end{array}} \right) \hfill \\ \end{gathered} $

Before our discussions,some basic well-known results related to Markov processes are needed,which will be presented concisely in the following.

For the above Markov system $\{Z(t),t\ge 0\}$,its probability vector at time $t$,denoted as ${{P}}(t)=\left( {p_i (t)} \right)_{1\times mn} $,is as follows, ${{P}}(t)=\left( {p_i (t)} \right)_{1\times mn} ={\rm {\bf \gamma }}\exp ({{G}}t),$ where $p_i (t)=P\{Z(t)=i\},i\in E\times S$.

Based on the partition of ${{G}}$,then we can define a matrix as $\begin{align} & {{\text{P}}_{{{W}_{i}}{{W}_{i}}}}(t)=(P\{Z(t)=j,Z(u)\in \{{{e}_{i}}\}\times {{W}_{i}},\\ & u\le t|X(0)=k\}),\ \ k,j\in \{{{e}_{i}}\}\times {{W}_{i}},\\ \end{align}$ and by Colquhoun and Hawkes2],we have ${{P}}_{W_i W_i } (t)=\mbox{exp(}{{G}}_{W_i W_i } t),$ where ${{P}}_{W_i W_i }(t) $ denotes probabilities that the repairable system remains within the working states $\{e_i \}\times W_i $ throughout the time from $0$ to $t$.

A.System Reliability

The system reliability is defined as the probability that the system is working during the time interval $[0,t]$. Thus,we assume that the states corresponding to $\{(e_i ,j):i=1,2,$ $... ,m;j\in F_i \}$ are absorbing states. To obtain the system reliability,we define a new Markov process $\{Z_1 (t),t\ge 0\}$ with the state space $E\times S$. The transition rate matrix is ${{\tilde{G}}_{1}}=\left( \begin{matrix} {{G}_{{{W}_{1}}{{W}_{1}}}} & {{G}_{{{W}_{1}}{{F}_{1}}}} & {{G}_{{{W}_{1}}{{W}_{2}}}} & {{G}_{{{W}_{1}}{{F}_{2}}}} & \cdots & {{G}_{{{W}_{1}}{{W}_{m}}}} & {{G}_{{{W}_{1}}{{F}_{m}}}} \\ {{0}_{{{F}_{1}}{{W}_{1}}}} & {{0}_{{{F}_{1}}{{F}_{1}}}} & {{0}_{{{F}_{1}}{{W}_{2}}}} & {{0}_{{{F}_{1}}{{F}_{2}}}} & \cdots & {{0}_{{{F}_{1}}{{W}_{m}}}} & {{0}_{{{F}_{1}}{{F}_{m}}}} \\ {{G}_{{{W}_{2}}{{W}_{1}}}} & {{G}_{{{W}_{2}}{{F}_{1}}}} & {{G}_{{{W}_{2}}{{W}_{2}}}} & {{G}_{{{W}_{2}}{{F}_{2}}}} & \cdots & {{G}_{{{W}_{2}}{{W}_{m}}}} & {{G}_{{{W}_{2}}{{F}_{m}}}} \\ {{0}_{{{F}_{2}}{{W}_{1}}}} & {{0}_{{{F}_{2}}{{F}_{1}}}} & {{0}_{{{F}_{2}}{{W}_{2}}}} & {{0}_{{{F}_{2}}{{F}_{2}}}} & \cdots & {{0}_{{{F}_{2}}{{W}_{m}}}} & {{0}_{{{F}_{2}}{{F}_{m}}}} \\ \quad \vdots & \quad \vdots & \quad \vdots & \quad \vdots & ~\vdots & \quad \vdots & \quad \vdots \\ {{G}_{{{W}_{m}}{{W}_{1}}}} & {{G}_{{{W}_{m}}{{F}_{1}}}} & {{G}_{{{W}_{m}}{{W}_{2}}}} & {{G}_{{{W}_{m}}{{F}_{2}}}} & ... & {{G}_{{{W}_{m}}{{W}_{m}}}} & {{G}_{{{W}_{m}}{{F}_{m}}}} \\ {{0}_{{{F}_{m}}{{W}_{1}}}} & {{0}_{{{F}_{m}}{{F}_{1}}}} & {{0}_{{{F}_{m}}{{W}_{2}}}} & {{0}_{{{F}_{m}}{{F}_{2}}}} & ... & {{0}_{{{F}_{m}}{{W}_{m}}}} & {{0}_{{{F}_{m}}{{F}_{m}}}} \\ \end{matrix} \right),$ where 0 denotes zero matrix with appropriate dimension. Then the system reliability is given by $R_{\rm sys} ([0,t])=\sum\limits_{e_i \in E} {\sum\limits_{j\in W_i } {P\{(X(t),Y(t))=(e_i ,j)\}} } .$ It is well-known that $P\{(X(t),Y(t))=({{e}_{i}},j)\}=\gamma {{\text{e}}^{t{{{\tilde{G}}}_{1}}}}({{e}_{i}},j)$ for any $e_i \in E$ and $j\in S$. Therefore,we have an explicit representation for the system reliability ${{R}_{\text{sys}}}([0,t])=\sum\limits_{{{e}_{i}}\in E}{\sum\limits_{j\in {{W}_{i}}}{<\text{b}>\gamma <\text{/b}>{{\text{e}}^{t{{{\tilde{G}}}_{1}}}}({{e}_{i}},j)}}.$ In the following,we are interested in the probability that the system operates in general time interval $[t_1 ,t_2]$ $(t_1 \le t_2 )$,it is called interval reliability in 11]. In fact,we can transform case $[t_1 ,t_2]$ into case $[0,t]$,so that we only need to know ${{P}}(t_1 )$ $=$ $\gamma {{\text{e}}^{{{t}_{1}}G}}$, which is the probability vector of the system staying in each state at instant time $t_1 $,then the general interval reliability of the system is given by $R_{\rm sys} ([t_1 ,t_2])=\sum\limits_{e_i \in E} {\sum\limits_{j\in W_i } {{{P}}(t_1 ){{E}}{\rm e}^{(t_2 -t_1 ){{\tilde {G}}}_1 }(e_i ,j)} } ,$ where $E=\left( \begin{matrix} {{I}_{{{n}_{1}}{{n}_{1}}}} & {{0}_{{{n}_{1}}(n-{{n}_{1}})}} & {{0}_{{{n}_{1}}{{n}_{2}}}} & {{0}_{{{n}_{1}}(n-{{n}_{2}})}} & \cdots & {{0}_{{{n}_{1}}{{n}_{m}}}} & {{0}_{{{n}_{1}}(n-{{n}_{m}})}} \\ {{0}_{(n-{{n}_{1}}){{n}_{1}}}} & {{0}_{(n-{{n}_{1}})(n-{{n}_{1}})}} & {{0}_{(n-{{n}_{1}}){{n}_{2}}}} & {{0}_{(n-{{n}_{1}})(n-{{n}_{2}})}} & \cdots & {{0}_{(n-{{n}_{1}}){{n}_{m}}}} & {{0}_{(n-{{n}_{1}})(n-{{n}_{m}})}} \\ {{0}_{{{n}_{2}}{{n}_{1}}}} & {{0}_{{{n}_{2}}(n-{{n}_{1}})}} & {{I}_{{{n}_{2}}{{n}_{2}}}} & {{0}_{{{n}_{2}}(n-{{n}_{2}})}} & \cdots & {{0}_{{{n}_{2}}{{n}_{m}}}} & {{0}_{{{n}_{2}}(n-{{n}_{m}})}} \\ {{0}_{(n-{{n}_{2}}){{n}_{1}}}} & {{0}_{(n-{{n}_{2}})(n-{{n}_{1}})}} & {{0}_{(n-{{n}_{2}}){{n}_{2}}}} & {{0}_{(n-{{n}_{2}})(n-{{n}_{2}})}} & \cdots & {{0}_{(n-{{n}_{2}}){{n}_{m}}}} & {{0}_{(n-{{n}_{2}})(n-{{n}_{m}})}} \\ \quad ~~\vdots & \quad ~~\vdots & \quad ~~\vdots & \quad ~~\vdots & ~\vdots & \quad ~~\vdots & \quad ~~\vdots \\ {{0}_{{{n}_{m}}{{n}_{1}}}} & {{0}_{{{n}_{m}}(n-{{n}_{1}})}} & {{0}_{{{n}_{m}}{{n}_{2}}}} & {{0}_{{{n}_{m}}(n-{{n}_{2}})}} & \cdots & {{I}_{{{n}_{m}}{{n}_{m}}}} & {{0}_{{{n}_{m}}(n-{{n}_{m}})}} \\ {{0}_{(n-{{n}_{m}}){{n}_{1}}}} & {{0}_{(n-{{n}_{m}})(n-{{n}_{1}})}} & {{0}_{(n-{{n}_{m}}){{n}_{2}}}} & {{0}_{(n-{{n}_{m}})(n-{{n}_{2}})}} & \cdots & {{0}_{(n-{{n}_{m}}){{n}_{m}}}} & {{0}_{(n-{{n}_{m}})(n-{{n}_{m}})}} \\ \end{matrix} \right)$ it is to keep the system starting from the working states of $\{e_i \}$ $\times$ $W_i $,$i=1,2,... ,m$.

In the following,we consider the multiple-interval reliability of the system.

Definition 1. For the above Markov system $\{Z(t),t\ge 0\}$,the multiple-interval reliability at given intervals $[a_1 ,b_1],[a_2 ,b_2],$ $... ,[a_m ,b_m]$ $(a_1 \le b_1 <a_2 \le b_2 <\cdots <a_m \le b_m )$,denoted as $R_{\rm sys} (\prod\nolimits_{i=1}^m {[a_i ,b_i]} )$,is defined as the probability of the system being at working states $W_1 ,W_2 ,... ,W_m $ and in environments $e_1 ,e_2 ,... ,e_m $ at the given multiple intervals $[a_1 ,b_1],$ $[a_2 ,b_2],... ,[a_m ,b_m]$,respectively,i.e., $\begin{align} & {{R}_{\text{sys}}}\left( \prod\limits_{i=1}^{m}{[{{a}_{i}},{{b}_{i}}]} \right)=P\{(X(u),Y(u))\in \{{{e}_{i}}\}\times {{W}_{i}}\text{,} \\ & \forall u\in [{{a}_{i}},{{b}_{i}}],i=1,2,...,m\}. \\ \end{align}$

Theorem 1. For the above Markov system $\{Z(t),t\ge 0\}$,the multiple-interval reliability is $\begin{align} & {{R}_{\text{sys}}}\left( \prod\limits_{i=1}^{m}{[{{a}_{i}},{{b}_{i}}]} \right)=\gamma \prod\limits_{i=1}^{m-1}{[\exp (G({{a}_{i}}-{{b}_{i-1}}))} \\ & \ \ \times {{\Delta }_{i}}\exp ({{G}_{{{W}_{i}}{{W}_{i}}}}({{b}_{i}}-{{a}_{i}})){{\Omega }_{i}}]\ \ \\ & \times \exp (G({{a}_{m}}-{{b}_{m-1}})){{\Delta }_{m}}\exp ({{G}_{{{W}_{m}}{{W}_{m}}}}({{b}_{m}}-{{a}_{m}})){{\text{1}}_{{{n}_{m}}}},\\ \end{align}$ where ${{\Delta }_{1}}=\left( \begin{matrix} {{I}_{{{n}_{1}}{{n}_{1}}}} \\ {{0}_{(n-{{n}_{1}}){{n}_{1}}}} \\ {{0}_{{{n}_{2}}{{n}_{1}}}} \\ {{0}_{(n-{{n}_{2}}){{n}_{1}}}} \\ \quad ~~\vdots \\ {{0}_{{{n}_{m}}{{n}_{1}}}} \\ {{0}_{(n-{{n}_{m}}){{n}_{1}}}} \\ \end{matrix} \right),\ \ {{\Delta }_{2}}=\left( \begin{matrix} {{0}_{{{n}_{1}}{{n}_{2}}}} \\ {{0}_{(n-{{n}_{1}}){{n}_{2}}}} \\ {{I}_{{{n}_{2}}{{n}_{2}}}} \\ {{0}_{(n-{{n}_{2}}){{n}_{2}}}} \\ \quad ~~\vdots \\ {{0}_{{{n}_{m}}{{n}_{2}}}} \\ {{0}_{(n-{{n}_{m}}){{n}_{2}}}} \\ \end{matrix} \right),$ $...,\ \ {{\Delta }_{m}}=\left( \begin{matrix} {{0}_{{{n}_{1}}{{n}_{m}}}} \\ {{0}_{(n-{{n}_{1}}){{n}_{m}}}} \\ {{0}_{{{n}_{2}}{{n}_{2}}}} \\ {{0}_{(n-{{n}_{2}}){{n}_{m}}}} \\ \quad ~~\vdots \\ {{I}_{{{n}_{m}}{{n}_{m}}}} \\ {{0}_{(n-{{n}_{m}}){{n}_{m}}}} \\ \end{matrix} \right),$ $\begin{align} & {{\Omega }_{1}}=({{I}_{{{n}_{1}}{{n}_{1}}}},{{0}_{{{n}_{1}}(n-{{n}_{1}})}},{{0}_{{{n}_{1}}{{n}_{2}}}},{{0}_{{{n}_{1}}(n-{{n}_{2}})}},...,\\ & \qquad \ \ {{0}_{{{n}_{1}}{{n}_{m-1}}}},{{0}_{{{n}_{1}}(n-{{n}_{m-1}})}},{{0}_{{{n}_{1}}{{n}_{m}}}},{{0}_{{{n}_{1}}(n-{{n}_{m}})}}),\\ & {{\Omega }_{2}}=({{0}_{{{n}_{2}}{{n}_{1}}}},{{0}_{{{n}_{2}}(n-{{n}_{1}})}},{{I}_{{{n}_{2}}{{n}_{2}}}},{{0}_{{{n}_{2}}(n-{{n}_{2}})}},...,\\ & \qquad \ \ {{0}_{{{n}_{2}}{{n}_{m-1}}}},{{0}_{{{n}_{2}}(n-{{n}_{m-1}})}},{{0}_{{{n}_{2}}{{n}_{m}}}},{{0}_{{{n}_{2}}(n-{{n}_{m}})}}),\\ & {{\Omega }_{m-1}}=({{0}_{{{n}_{m-1}}{{n}_{1}}}},{{0}_{{{n}_{m-1}}(n-{{n}_{1}})}},{{0}_{{{n}_{m-1}}{{n}_{2}}}},{{0}_{{{n}_{m-1}}(n-{{n}_{2}})}},...,\\ & \qquad \ \ {{I}_{{{n}_{m-1}}{{n}_{m-1}}}},{{0}_{{{n}_{m-1}}(n-{{n}_{m-1}})}},{{0}_{{{n}_{m-1}}{{n}_{m}}}},{{0}_{{{n}_{m-1}}(n-{{n}_{m}})}}),\\ \end{align}$ $b_0 =0$,and ${{1}}_{n_m } $ is a column vector of $n_m $ ones.

Proof. Since $\exp ({{G}}(a_i -b_{i-1} ))\Delta _i \exp ({{G}}_{W_i W_i } (b_i -a_i ))$ is the transition probability vector from time $a_i -b_{i-1} $ to time $b_i -b_{i-1} $, $i=1,2,... ,m$,and the system sojourns in the working states during all interval times $[a_i -b_{i-1} ,b_i -b_{i-1}]$ (because of the time homogeneity),and the function of matrix $\Delta _i $ is to keep the system starting from the working states of $\{e_i \}\times W_i $,the role of matrix ${{\Omega }}_i $ is to change matrix dimension $1\times n_i $ into $1\times mn$,and the column vector ${{1}}_{n_m } $ is used to sum up all possible probabilities that satisfies the requirements.

B.Environment Reliability

The system operates in the environment set $E$. We assume that some environments are fatal to the system,i.e.,the system does not operate when it is in these environments. Let $\begin{align} & NA=\{{{e}_{k+1}},{{e}_{k+2}},...,{{e}_{m}}\} \\ & {{{\tilde{G}}}_{2}}=\left( \begin{matrix} {{G}_{{{W}_{1}}{{W}_{1}}}} & {{G}_{{{W}_{1}}{{F}_{1}}}} & {{G}_{{{W}_{1}}{{W}_{2}}}} & {{G}_{{{W}_{1}}{{F}_{2}}}} & \cdots & {{G}_{{{W}_{1}}{{W}_{k}}}} & {{G}_{{{W}_{1}}{{F}_{k}}}} \\ {{G}_{{{F}_{1}}{{W}_{1}}}} & {{G}_{{{F}_{1}}{{F}_{1}}}} & {{G}_{{{F}_{1}}{{W}_{2}}}} & {{G}_{{{F}_{1}}{{F}_{2}}}} & \cdots & {{G}_{{{F}_{1}}{{W}_{k}}}} & {{G}_{{{F}_{1}}{{F}_{k}}}} \\ {{G}_{{{W}_{2}}{{W}_{1}}}} & {{G}_{{{W}_{2}}{{F}_{1}}}} & {{G}_{{{W}_{2}}{{W}_{2}}}} & {{G}_{{{W}_{2}}{{F}_{2}}}} & \cdots & {{G}_{{{W}_{2}}{{W}_{k}}}} & {{G}_{{{W}_{2}}{{F}_{k}}}} \\ {{G}_{{{F}_{2}}{{W}_{1}}}} & {{G}_{{{F}_{2}}{{F}_{1}}}} & {{G}_{{{F}_{2}}{{W}_{2}}}} & {{G}_{{{F}_{2}}{{F}_{2}}}} & \cdots & {{G}_{{{F}_{2}}{{W}_{k}}}} & {{G}_{{{F}_{2}}{{F}_{k}}}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{G}_{{{W}_{k}}{{W}_{1}}}} & {{G}_{{{W}_{k}}{{F}_{1}}}} & {{G}_{{{W}_{k}}{{W}_{2}}}} & {{G}_{{{W}_{k}}{{F}_{2}}}} & \cdots & {{G}_{{{W}_{k}}{{W}_{k}}}} & {{G}_{{{W}_{k}}{{F}_{k}}}} \\ {{G}_{{{F}_{k}}{{W}_{1}}}} & {{G}_{{{F}_{k}}{{F}_{1}}}} & {{G}_{{{F}_{k}}{{W}_{2}}}} & {{G}_{{{F}_{k}}{{F}_{2}}}} & \cdots & {{G}_{{{F}_{k}}{{W}_{k}}}} & {{G}_{{{F}_{k}}{{F}_{k}}}} \\ \end{matrix} \right) \\ \end{align}$

Without loss of generality,we assume that the environment set $NA$ is unacceptable to the system. The system failure states are not concerned in this situation. The subscript $F$ is still retained in order to facilitate discussion. Thus,the environment reliability is given by ${{R}_{\text{env}}}([0,t])={{\gamma }_{2}}\exp (t{{\tilde{G}}_{2}}){{\text{1}}_{kn}},$ where ${\rm {\bf \gamma }}_2 =(1,0,... ,0)_{1\times kn} $.

In the following,when both the system failure states and fatal environment states are jointly concerned,we formulate the reliability of the system. We suppose that the environment set $NA$ is unacceptable to the system,and the system failure states are the same as in Section III-A. Let ${{\tilde{G}}_{3}}=\left( \begin{matrix} {{G}_{{{W}_{1}}{{W}_{1}}}} & {{G}_{{{W}_{1}}{{F}_{1}}}} & {{G}_{{{W}_{1}}{{W}_{2}}}} & {{G}_{{{W}_{1}}{{F}_{2}}}} & ... & {{G}_{{{W}_{1}}{{W}_{k}}}} & {{G}_{{{W}_{1}}{{F}_{k}}}} & 0 \\ {{0}_{{{F}_{1}}{{W}_{1}}}} & {{0}_{{{F}_{1}}{{F}_{1}}}} & {{0}_{{{F}_{1}}{{W}_{2}}}} & {{0}_{{{F}_{1}}{{F}_{2}}}} & ... & {{0}_{{{F}_{1}}{{W}_{k}}}} & {{0}_{{{F}_{1}}{{F}_{k}}}} & 0 \\ {{G}_{{{W}_{2}}{{W}_{1}}}} & {{G}_{{{W}_{2}}{{F}_{1}}}} & {{G}_{{{W}_{2}}{{W}_{2}}}} & {{G}_{{{W}_{2}}{{F}_{2}}}} & ... & {{G}_{{{W}_{2}}{{W}_{k}}}} & {{G}_{{{W}_{2}}{{F}_{k}}}} & 0 \\ {{0}_{{{F}_{2}}{{W}_{1}}}} & {{0}_{{{F}_{2}}{{F}_{1}}}} & {{0}_{{{F}_{2}}{{W}_{2}}}} & {{0}_{{{F}_{2}}{{F}_{2}}}} & ... & {{0}_{{{F}_{2}}{{W}_{k}}}} & {{0}_{{{F}_{2}}{{F}_{k}}}} & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{G}_{{{W}_{k}}{{W}_{1}}}} & {{G}_{{{W}_{k}}{{F}_{1}}}} & {{G}_{{{W}_{k}}{{W}_{2}}}} & {{G}_{{{W}_{k}}{{F}_{2}}}} & ... & {{G}_{{{W}_{k}}{{W}_{k}}}} & {{G}_{{{W}_{k}}{{F}_{k}}}} & 0 \\ {{0}_{{{F}_{k}}{{W}_{1}}}} & {{0}_{{{F}_{k}}{{F}_{1}}}} & {{0}_{{{F}_{k}}{{W}_{2}}}} & {{0}_{{{F}_{k}}{{F}_{2}}}} & ... & {{0}_{{{F}_{k}}{{W}_{k}}}} & {{0}_{{{F}_{k}}{{F}_{k}}}} & 0 \\ 0 & 0 & 0 & 0 & ... & 0 & 0 & 0 \\ \end{matrix} \right),$ where ${\rm { 0}}$ denotes zero matrixes with appropriate dimension. Then the system reliability is given by $\begin{align} & {{{{R}'}}_{\text{sys}}}([0,t])=\sum\limits_{{{e}_{i}}\in \{{{e}_{1}},{{e}_{2}},...,{{e}_{m}}\}}{\sum\limits_{j\in {{W}_{i}}}{P\{(X(t),Y(t))=({{e}_{i}},j)\}}}\qquad = \\ & \sum\limits_{{{e}_{i}}\in \{{{e}_{1}},{{e}_{2}},...,{{e}_{m}}\}}{\sum\limits_{j\in {{W}_{i}}}{<\text{b}>\gamma <\text{/b}>{{\text{e}}^{t{{{\tilde{G}}}_{3}}}}({{e}_{i}},j)}}. \\ \end{align}$

Availability is another important reliability index. One may be interested in the probability that the system is operating at time $t$. Therefore,the system availability is given by $\begin{align} & {{A}_{\text{sys}}}(t)=P\{\text{thesystemisoperatingattime}t\quad \ = \\ & P\{(X(t),Y(t))\in \bigcup\limits_{i=1}^{m}{(\{{{e}_{i}}\}\times {{W}_{i}})}\}\quad \ = \\ & \gamma \exp (Gt){{\left( 1_{{{n}_{1}}}^{\text{T}}~0_{n-{{n}_{1}}}^{\text{T}}~1_{{{n}_{2}}}^{\text{T}}~0_{n-{{n}_{2}}}^{\text{T}}~...~1_{{{n}_{m}}}^{\text{T}}~0_{n-{{n}_{m}}}^{\text{T}} \right)}^{\text{T}}},\\ \end{align}$ where ${\rm {1}}$ is a column vector with all elements equal to 1 and ${\rm {0}}$ is a column vector with all elements equal to 0.

In the following,we consider the multiple-point availability of the system.

Definition 2. For the above Markov system $\{Z(t),t\ge 0\}$,the multiple-point availability at given points $t_1 <t_2 <\cdots <t_m $,denoted as $A_{\rm sys} (t_1 ,t_2 ,... ,t_m )$,is defined as the probability of the system being at working states $W_1 ,W_2 ,... ,W_m $ and in environments $e_1 ,e_2 ,... ,e_m $ at the given multiple points $t_1 ,$ $t_2 ,$ $... ,$ $t_n $, respectively,i.e., $\begin{align} & {{A}_{\text{sys}}}({{t}_{1}},{{t}_{2}},...,{{t}_{m}})\qquad = \\ & P\{(X({{t}_{i}}),Y({{t}_{i}}))\in \{{{e}_{i}}\}\times {{W}_{i}},\ i=1,2,...,m\}. \\ \end{align}$

Theorem 2. For the above Markov system $\{Z(t),t\ge 0\}$,the multiple-point availability is $\begin{align} & {{A}_{\text{sys}}}({{t}_{1}},{{t}_{2}},...,{{t}_{m}})=\gamma \exp (G{{t}_{1}}){{E}_{1}}\exp (G({{t}_{2}}-{{t}_{1}})) \\ & {{E}_{2}}\qquad \times \cdots \times {{E}_{m-1}}\exp (G({{t}_{m}}-{{t}_{m-1}})){{E}_{m}},\\ \end{align}$ where $\begin{align} & {{E}_{1}}=\left( \begin{matrix} {{I}_{{{n}_{1}}\times {{n}_{1}}}} & {{0}_{{{n}_{1}}\times (mn-{{n}_{1}})}} \\ [1mm]{{0}_{(mn-{{n}_{1}})\times {{n}_{1}}}} & {{0}_{(mn-{{n}_{1}})\times (mn-{{n}_{1}})}} \\ \end{matrix} \right),\\ & {{E}_{2}}=\left( \begin{matrix} {{0}_{n\times n}} & {{0}_{n\times {{n}_{2}}}} & {{0}_{n\times ((m-1)n-{{n}_{2}})}} \\ [1mm]{{0}_{{{n}_{2}}\times n}} & {{I}_{{{n}_{2}}\times {{n}_{2}}}} & {{0}_{{{n}_{2}}\times ((m-1)n-{{n}_{2}})}} \\ [1mm]{{0}_{((m-1)n-{{n}_{2}})\times n}} & {{0}_{((n-1)m-{{n}_{2}})\times {{n}_{2}}}} & {{0}_{((m-1)n-{{n}_{2}})\times ((m-1)n-{{n}_{2}})}} \\ \end{matrix} \right),\\ \end{align}$ $\begin{align} & {{E}_{m-1}}=\left( \begin{matrix} {{0}_{(m-2)n\times (m-2)n}} & {{0}_{(m-2)n\times {{n}_{m-1}}}} & {{0}_{(m-2)n\times (2n-{{n}_{m-1}})}} \\ [1mm]{{0}_{{{n}_{m-1}}\times (m-2)n}} & {{I}_{{{n}_{m-1}}\times {{n}_{m-1}}}} & {{0}_{{{n}_{m-1}}\times (2n-{{n}_{m-1}})}} \\ [1mm]{{0}_{(2n-{{n}_{m-1}})\times (m-2)n}} & {{0}_{(2n-{{n}_{m-1}})\times {{n}_{m-1}}}} & {{0}_{(2n-{{n}_{m-1}})\times (2n-{{n}_{m-1}})}} \\ \end{matrix} \right),\\ & {{E}_{m}}=\left( \begin{array}{*{35}{l}} {{0}_{(m-1)n\times 1}} \\ [1mm]{{I}_{{{n}_{m}}\times 1}} \\ [1mm]{{0}_{(n-{{n}_{m}})\times 1}} \\ \end{array} \right),\\ \end{align}$ ${ { I}}$ is a unit matrix with appropriate dimension, ${\rm {0}}$ is a zero matrix with appropriate dimension.

Proof. Because of time homogeneity,${{\gamma }}\exp ({{G}}t_1 )$ is a probability vector which gives the probability of the system being at each state and at instant time $t_1 $,and $\exp ({{G}}(t_i -t_{i-1} ))$ $(i$ $=$ $2,3,... ,m)$,is the transition probabilities from time $t=0$ to time $t=t_i -t_{i-1} $. The function of matrix ${{E}}_i $ $(i=1,2,$ $... ,$ $m-1)$ is to keep the system starting from the working states of $\{e_i \}\times W_i $ and the role of matrix ${{E}}_m $ is to sum up all possible working probabilities. The product operations are used among the terms because of conditional independence.

Because the environment $e_i$ $(e_i \in NA)$ is unacceptable to the system,the environment availability of the system is given by $\begin{align} & {{A}_{\text{env}}}(t)=\ P\{(X(t),Y(t))\in \bigcup\limits_{i=1}^{k}{(\{{{e}_{i}}\}\times {{W}_{i}})}\} \\ & =\gamma \exp (Gt)\left( 1_{{{n}_{1}}}^{\text{T}}~~0_{n-{{n}_{1}}}^{\text{T}}~~1_{{{n}_{2}}}^{\text{T}}~~0_{n-{{n}_{2}}}^{\text{T}} \right.\ \\ & ...~~1_{{{n}_{k}}}^{\text{T}}~~0_{n-{{n}_{k}}}^{\text{T}}~~0_{{{n}_{k+1}}}^{\text{T}}~~0_{n-{{n}_{k+1}}}^{\text{T}}\ \\ & {{\left. ...~~0_{{{n}_{m}}}^{\text{T}}~~0_{n-{{n}_{m}}}^{\text{T}} \right)}^{\text{T}}}. \\ \end{align}$

In this section,an engineering example is presented to illustrate the results obtained in the previous sections.

The air-condition system is essential to us in some places, such as,Hainan province,Guangdong province,Beijing,Shanghai and so on. We suppose that an air-condition system operating in the environment process $\{X(t),t\ge 0\}$,and it has a state space $E=\{e_1 ,e_2 ,e_3 \}$. The states $e_1 $,$e_2 $,and $e_3 $ can denote spring,summer,and autumn,respectively. The transition rate matrix is ${{H}}=\left( {{\begin{array}{*{20}r} {-2} & 2 & 0 \\ 0 & {-1} & 1 \\ 1 & 0 & {-1} \\ \end{array} }} \right).$ When the system is in the environment $e_1 $,the deterioration level of the system is $S=\{1,2\}=W_1 $,and the transition rate matrix is ${{G}}_1 =\left( {{\begin{array}{*{20}r} {-3} & 3 \\ 1 & {-1} \\ \end{array} }} \right).$ When the system is in the environment $e_2 $,the deterioration level of the system is $S=\{1\}\cup \{2\}=W_2 \cup F_2 $,and the transition rate matrix is ${{G}}_2 =\left( {{\begin{array}{*{20}r} {-1} & 1 \\ 2 & {-2} \\ \end{array} }} \right).$ When the system is in the environment $e_3 $,the deterioration level of the system is $S=\{1,2\}=F_3 $,and the transition rate matrix is ${{G}}_3 =\left( {{\begin{array}{*{20}r} {-2} & 2 \\ 1 & {-1} \\ \end{array} }} \right).$ It is obvious that the environment $e_3 $ is unacceptable to the system,so the system reliability and the system availability are equal to the environment reliability and the environment availability,respectively. Therefore,we consider only the system reliability indexes in the following.

Thus,the bivariate process $\{Z(t),t\ge 0\}=\{( X(t),Y(t)),$ $t$ $\ge$ $0\}$ has state space $E\times S=\{(e_1 ,1),(e_1 ,2),(e_2 ,1),(e_2 ,2),(e_3 ,1),(e_3 ,2)\}.$ The initial probability vector is ${\rm {\bf \gamma }}=\left( {1,0,0,0,0,0} \right)$. By using Matlab software, we can get the curve of the system reliability $R_{\rm sys} ([0,t])$,which is shown in Fig.1.

Fig. 1

	Download: JPG larger image
Fig. 1. The curve of the system reliability $R_{\rm sys} ([0,t])$.

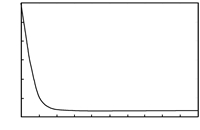
If the value of $a$ is given (denoted as $a=0.3)$,then the interval reliability $R_{\rm sys} ([0.3,b])$ is a function of $b$. Fig.2 is the curve of the system interval reliability $R_{\rm sys} ([0.3,b])$ as $b$ varies. So we have $R_{\rm sys} ([0.3,0.4],[0.9,1])=0.0879.$ Similarly,we can get the curve of the system availability shown in Fig.3. And we obtained that $A_{\rm sys} (0.3,0.5)=0.2554$.

Fig. 2

	Download: JPG larger image
Fig. 2. The curve of the system interval reliability $R_{\rm sys} ([0.3,b])$ as $b$ varies.

Fig. 3

	Download: JPG larger image
Fig. 3. The curve of the system interval reliability The curve of the system availability $A_{\rm sys} (t)$.

In this paper,the system which operates in multiple environments is studied. It is more general than the single environment studied in previous papers. A combined,bivariate stochastic process is constructed to represent the evolution of the system. Interesting reliability indexes are obtained by using aggregated stochastic process theory and matrix partition method. Especially,multiple-interval reliability and multiple-point availability are not covered by traditional reliabilities. A numerical example is also given to illustrate the results obtained in this paper. In future study,the temporally non-homogeneous continuous-time Markov chain environment system and the temporally homogeneous semi-Markov process environment system may be considered instead of the Markov environment system. Various performance measures are now conceivable; for example: system reliability,environment reliability,system multiple-interval reliability,system availability,environment availability, system-multiple point availability etc.