I. INTRODUCTION

Awide variety of today's engineering applications are implemented on digital platforms. In such an implementation, the sampled-data control theory has shown its effectiveness and developed considerably well as shown^{[1, 2]}. However, in these traditional sampled-data control frameworks, the control task is executed periodically regardless whether it is really required or not. Besides, the sampling period is chosen for a worst-case scenario, thus leading to conservatism. Moreover, these attributes arising from communication constraints of real networks lead to unnecessary utilization of channel and power consumption. Since the desired control specification cannot always be ensured using a fixed sampling period, the current trend is to adopt event-triggered control, see, e.g., ^{[3, 4, 5]}. These papers highlighted the advantages of event-triggered control and proposed systematic design methods, thus motivated the development of this theory.

Event-triggered control offers clear advantages with respect to traditional periodic control but at the same time introduces new practical problems, that is, it needs a special hardware as an event detector to decide the next sample time. Unfortunately, using this kind of hardware, such as field programmable gate array (FPGA), is not practical in many engineering applications. Therefore, an alternative approach called self-triggered control appears. Both the event-triggered control and self-triggered control have two basic components. A controller that computes the control input and a triggering mechanism that decides the control task release time. But the difference is that, in a self-triggered strategy^[6], the next release time is computed using the current sampled data and dynamics of the plant.

Since ^[4] obtained results on event-triggered control under the assumption that feedback control law preserves input-to-state stability with respect to measurement error of the plant state, fruitful results appear, see, e.g., ^{[7, 8, 9, 10, 11]}. Self-triggered control of homogeneous control systems was investigated^[7]and self-triggered scheme guaranteeing finite-gain $\mathcal{L}_2$ stability was presented^[8].

Most of the prior work on event-triggered and self-triggered control has a common assumption, that is, the full state information is available. However, in practice, the full state is often not available for measurement. Thus, it is important to extend to event-triggered output-based control with/without an observer.

A dynamic output-feedback controller based on event-triggered control was implemented in ^[12], while an event condition based on the state error of the observer was proposed and the system with norm-bounded uncertainty was investigated in ^[13]. A more recent work can be found in ^[14], which used the hybrid system method proposed in ^[15]. In the work, the event-triggered systems is reformulated as a hybrid dynamical system and linear matrix inequalities are applied to study its stability and performance. In ^[16], observer-based event-triggered control was considered, and global uniform ultimate bounded stability of the event-triggered system was obtained.

Inspired by ^[14] and ^[16], we propose an event-triggered control strategy which is based on a function observer. Actually, in many engineering applications, the purpose of getting the estimate of state is to generate a feedback control law. Thus, in this situation, it is better to generate a linear combination of the state rather than to generate the estimate of the plant state. We will show that, in case we skip the intermediate procedure of generating estimate of the state, and directly transmit the estimate of the linear combination of state to the plant as control input, we will have better control performance and less numbers of sampling events.

The rest of this paper is organized as follows: we first introduce some notations and background on hybrid systems in Section II; and then, the problem formulation is stated in Section III, besides, the event-triggered mechanism and closed-loop model are presented in this section; two approaches are, proposed, to, analyze, the event-triggered, control, system, in Section IV, with guaranteed positive minimum inter-event time; a numerical example is illustrated in Section V; finally, Section VI summarizes the main results.

II. NOTATIONS AND PRELIMINARIES

As usual, we shall use the notation $\| \cdot \|$ to denote the Eucli- dean norm of an element $x \in {\bf R}^n$. ${\bf R}^n$ denotes the $n$-dimensional Euclidean space and ${\bf R}^{m \times n}$ denotes the set of all $m \times n$ dimensional real matrices. ${\bf R}^+$ denotes the set of positive real numbers. For real matrix $X$, $X^{\rm T}$ and $X^{-1}$ are defined as the transpose and inverse of $X$. And $\lambda_{\rm min}(X)$ and $\lambda_{\rm max}(X)$ denotes the smallest and the largest eigenvalue of $X$, respectively. $X \succ Y, (X \prec Y)$ indicates that $X-Y$ is a positive (negative) definite matrix. Besides, $X \nprec Y$ denotes that $X-Y$ is not negative definite. Finally, for a signal $x$, we denote the limit from above at time $t \in {\bf R}^+$ by $x^+(t)=\lim_{h \rightarrow 0^+}x(t+h)$.

${\bf Definition 1.}$^[15] Consider a hybrid system $\mathcal{H}$ with the form

\begin{align} \begin{array}{lll} \dot{x} \in \mathcal{F}(x), & x \in \mathcal{C}, \\ x^+ \in \mathcal{G}(x), & x \in \mathcal{D}, \end{array} \end{align}

(1)

where $\mathcal{C}$ is called the flow set, $\mathcal{F}$ the flow map, $\mathcal{D}$ the jump set, and $\mathcal{G}$ the jump map. Besides, let $\mathcal{A} = \mathcal{C} \lor \mathcal{D}$, thus $x \in \mathcal{A}$.

A compact set $\mathcal{S} \subseteq \mathcal{A}$ is stable for $\mathcal{H}$ if for each $\epsilon > 0$ there exists $\delta > 0$ such that $\min \{ \|x(0)-y \|:y \in \mathcal{S} \} \le \delta$ implies $\min \{ \|x(t)-y \|:y \in \mathcal{S} \} \le \epsilon$.

A compact set $\mathcal{S}$ is attractive if there exists a neighborhood of $\mathcal{S}$ from which each solution is bounded and converges to $\mathcal{S}$, that is, $\lim_{t \rightarrow \infty}{\min \{ \|x(t)-y \|:y \in \mathcal{S} \}}=0$.

A compact $\mathcal{S}$ is asymptotically stable if it is stable and attractive.

${\bf Lemma 1}$^[15]. Consider the hybrid system $\mathcal{H}$ defined in Definition 1. The compact set $\mathcal{S}$ satisfies $\mathcal{G}(\mathcal{S} \land \mathcal{D}) \subset \mathcal{S}$. If there exists a Lyapunov function candidate $V(x)$ for $(\mathcal{H}, \mathcal{S})$ such that

\begin{align} &\dot{V}(x)<0, \quad \textrm{for all}~x \in \mathcal{C} \setminus \mathcal{S}, \nonumber \\ &V(\mathcal{G}(x))-V(x)<0, \quad \textrm{for all}~x \in \mathcal{D} \setminus \mathcal{S}, \end{align}

(2)

then the set $\mathcal{S}$ is asymptotically stable.

III. PROBLEM FORMULATION

Consider the following linear time-invariant system with the initial state $x(t_0)=x_0$ that satisfies, for all $t\ge t_0$,

\begin{align} \left\{ \begin{array}{l} \dot{x}=Ax+Bu+H\omega, \\ y=Cx, \end{array} \right. \end{align}

(3)

where $x \in {\bf R}^n$, $y \in {\bf R}^q$, $u \in {\bf R}^p$ and $\omega \in {\bf R}^r$ denote the state, output, control input and unknown disturbance, respectively. The pairs $(A, B )$ and $(A, C)$ are assumed to be controllable and observable, respectively.

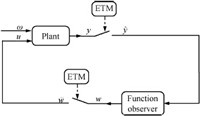
In this paper we focus on event-triggered control strategies that can be described with the help of Fig. 1. In this setup, the plant output $y$ is sampled only at the time instants $t_k, k \in {\bf N}$. This information $\hat{y}(t_k)$ is sent to a function observer (we can see a book on linear systems for more details, for example, see [17]), %\cite{Zheng}) which is described by the following equation in the interval $[t_k, t_{k+1})$,

\begin{align} \left\{ \begin{array}{lll} \dot{z}\!\!\!\!&=&\!\!\!\!Fz+Nu+G\hat{y}, \\ w\!\!\!\!&=&\!\!\!\!Ez+M\hat{y}, \end{array} \right. \end{align}

(4)

where $z \in {\bf R}^n$ and $w \in {\bf R}^p$ denote the state and output of the function observer, respectively. Besides, all the eigenvalues of $F$ have negative real part.

If we have that $\lim_{t \rightarrow \infty}(Px(t)-z(t))=0$, where $P$ is chosen satisfying $PA-FP=GC$, $K=EP+MC$, $N=PB$, then we can get

\begin{align} \lim_{t \rightarrow \infty}(Kx(t)-w(t))=0. \end{align}

(5)

The gain matrix $K$ is designed using an emulation-based approach, that is, it is chosen such that asymptotical stability is guaranteed for a continuous-time controller with access to full state measurements. The function observer computes an estimate of the signal $Kx$ at the current sampling time. This estimated value will be sampled at $t_k$, and then be sent to the plant as a control input. The control input is kept constant between sampling time by a zero-order hold, thus,

\begin{align} u(t)=\tilde{w}(t_k), t \in [t_k, t_{k+1}). \end{align}

(6)

Here, $t_k$ is the time when the event happens.

Define the event-triggered-induced errors as

\begin{align} \hat{e}(t)=\hat{y}(t_k)-y(t) \quad \textrm{and} \quad \tilde{e}(t)=\tilde{w}(t_k)-w(t), \end{align}

(7)

and select the event-triggering mechanism satisfying

\begin{align} &t_{k+1}=\inf\{t>t_k | , \|\hat{e}(t)\|^2=\sigma\|y(t)\|^2+\epsilon, \nonumber \\ &\qquad \quad \textrm{or} \quad \|\tilde{e}(t)\|^2=\zeta\|w(t)\|^2+\delta \} \end{align}

(8)

for some $\sigma, \epsilon, \zeta, \delta \ge 0$, and suppose $t_0=0$. Let the observation error be defined as $e(t)=Px(t)-z(t)$. Thus, the resulting closed-loop system becomes:

\[\left\{ {\begin{array}{*{20}{l}} {\dot x}& = &{(A + BMC)x + BEz + BM\hat e + B\tilde e + H\omega , }\\ {\dot z}& = &{(NM + G)Cx + (F + NE)z}\\ {}&{}&{ + (NM + G)\hat e + N\tilde e, }\\ {\dot e}& = &{Fe - G\hat e + PH\omega .} \end{array}} \right.\]

(9)

The problem addressed here aims at developing conditions on event-triggered control strategy in terms of linear matrix inequalities that renders the closed-loop system satisfying specified stability, which depends on the method employed. Actually, we will use two methods to analyze this system by deriving conditions such that the closed-loop system is asymptotically stable in a compact set and ultimate bounded stable, respectively.

${\bf Remark 1.}$ The event-triggering mechanism proposed above in (8) requires that it is feasible to transmit both $y$ and $w$ synchronically. The transmitted $w$ should be computed based on the newly received $\hat{y}$. To explain this requirement in more detail, let us consider the opposite case, i.e., the two signals are not transmitted synchronically.

From the event-triggered conditions in (8), we could find that the thresholds are reached in turn, and $y$ and $w$ are triggered to be sent more and more frequently as $\hat{y}$ has a direct influence on $w$. Therefore, it could happen that $y$ or $w$ are transmitted twice or more at one time instant, and this cannot be implemented from a practical point of view.

IV. EVENT-TRIGGERED CONTROL DESIGN

A. Hybrid Dynamical System Method

In this section, we reformulate the event-triggered control system using the method in ^[15], $%\cite{Teel Hyb}$, thus get a hybrid system model satisfying the following set of state equations,

\[\begin{array}{*{20}{l}} {\dot \chi }& = &{\tilde A\chi + \tilde H\omega , }&{{\rm{when}}\;\chi \in {{\cal S}_F}, }\\ {{\chi ^ + }}& = &{\tilde B\chi , }&{{\rm{when}}\;\chi \in {{\cal S}_J}, } \end{array}\]

(10)

where

\[\tilde A = {\left[{\begin{array}{*{20}{l}} {\tilde A_1^{\rm{T}}}&{\tilde A_2^{\rm{T}}}&{\tilde A_3^{\rm{T}}}&{\tilde A_4^{\rm{T}}}&{\tilde A_5^{\rm{T}}} \end{array}} \right]^{\rm{T}}}, \]

(11)

with

\[\begin{array}{*{20}{l}} {{{\tilde A}_1} = \left[{\begin{array}{*{20}{l}} {A + BMC}&{BE}&0&{BM}&B \end{array}} \right], }\\ {{{\tilde A}_2} = \left[{\begin{array}{*{20}{l}} {(NM + G)C}&{F + NE}&0&{NM + G}&N \end{array}} \right], }\\ {{{\tilde A}_3} = \left[{\begin{array}{*{20}{l}} 0&0&F&{ - G}&0 \end{array}} \right], }\\ {{{\tilde A}_4} = - C{{\tilde A}_1}, \quad {{\tilde A}_5} = - E{{\tilde A}_2}, } \end{array}\]

and

\[\tilde H = {\left[{\begin{array}{*{20}{l}} {{H^{\rm{T}}}}&0&{{H^{\rm{T}}}{P^{\rm{T}}}}&{ - {H^{\rm{T}}}{C^{\rm{T}}}}&0 \end{array}} \right]^{\rm{T}}}, \]

(12)

\[\tilde B = \left[{\begin{array}{*{20}{l}} I&0&0&0&0\\ 0&I&0&0&0\\ 0&0&I&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array}} \right].\]

(13)

In the above equations, $\chi \in \mathcal{A} \subseteq {\bf R}^{n_\chi}$ denotes the state vector of the system. $\mathcal{S}_F \subseteq {\bf R}^{n_\chi}$ and $\mathcal{S}_J \subseteq {\bf R}^{n_\chi}$ denote the flow and jump set, respectively. Besides, let $\mathcal{A}=\mathcal{S}_F \lor \mathcal{S}_J$. For notational convenience the state components of $\chi$ will be denoted as two groups, that is, $\chi_x$ and $\chi_e$

\[\chi = {\left[{\begin{array}{*{20}{c}} {{x^{\rm{T}}}}&{{z^{\rm{T}}}}&{{e^{\rm{T}}}}&{{{\hat e}^{\rm{T}}}}&{{{\tilde e}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}} = {\left[{\begin{array}{*{20}{l}} {\chi _x^{\rm{T}}}&{\chi _e^{\rm{T}}} \end{array}} \right]^{\rm{T}}}.\]

(14)

The flow set is

\begin{align} \mathcal{S}_F=\{\chi \in {\bf R}^{n_\chi}| \chi^{\rm T} Q_y \chi<\epsilon ~, \textrm{and} ~, \chi^{\rm T} Q_w \chi<\delta \}, \end{align}

(15)

and the jump set is

\begin{align} \mathcal{S}_J=\{\chi \in {\bf R}^{n_\chi}| \chi^{\rm T} Q_y \chi=\epsilon ~, \textrm{or} ~, \chi^{\rm T} Q_w \chi=\delta \}, \end{align}

(16)

where

\begin{align} Q_y=\left[ \begin{array}{cllll} -\sigma C^{\rm T} C & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & I & 0\\ 0 & 0 & 0 & 0 & 0 \end{array} \right], \end{align}

(17)

\begin{align} Q_w=\left[ \begin{array}{cl} -\zeta Q_0 & 0\\ 0 & I \end{array} \right], \end{align}

(18)

and

\begin{align} Q_0=\left[ \begin{array}{llll} C^{\rm T} M^{\rm T} MC & C^{\rm T} M^{\rm T} E & 0 & C^{\rm T} M^{\rm T} M\\ E^{\rm T} MC & E^{\rm T} E & 0 & E^{\rm T} M\\ 0 & 0 & 0 & 0\\ M^{\rm T} MC & M^{\rm T} E & 0 & M^{\rm T} M \end{array} \right]. \end{align}

(19)

Let us now define the notion of $\mathcal{L}_\infty$-gain of a system, and for which we introduce a performance output $z_p \in {\bf R}^m$ given by

\begin{align} z_p = C_z \chi + D_z \omega. \end{align}

(20)

${\bf Definition 2.}$ The $\mathcal{L}_\infty$-gain of the system (10), with (20) is defined as

\begin{align} \kappa = &\inf \{ \bar{\kappa} \in {\bf R}^+ ~|~ \exists \delta: \mathcal{A}\rightarrow{\bf R}^+, ~\textrm{such that} ~\|z_p\|_{\mathcal{L}_\infty} \nonumber \\ &\leq \bar{\kappa} \|\omega\|_{\mathcal{L}_\infty} + \delta(\chi(0)), ~\forall \chi(0) \in \mathcal{A}, ~\omega \in \mathcal{L_{\infty}} \}, \end{align}

(21)

where $z_p$ is given by ~(20), in which $\chi$ is a solution to ~(10), with initial condition $\chi(0) \in \mathcal{A}$ and disturbance $\omega \in \mathcal{L}_\infty$.

${\bf Theorem 1.}$ Consider the event-triggered control system (10), with (11), (12), (13), (15), (16) and (20) and assume its solutions exist for all $t \in {\bf R}^+$ and all $\omega \in {\bf R}^r$, satisfying $\|\omega\|_{\mathcal{L}_\infty} < \infty$. Moreover, assume that a minimum inter-event time $\tau > 0$ exists. Now suppose there exist a positive definite matrix $P_x \in {\bf R}^{(n_x+n_z+n_e) \times (n_x+n_z+n_e)}$, a positive semidefinite matrix $P_\chi \in {\bf R}^{n_\chi \times n_\chi}$, and $\tilde{P}:={\rm diag}\{P_x, 0\}+P_\chi$, scalars ~$\kappa, ~\iota, ~\theta > 0$ and ~$\lambda_1, ~\lambda_2, ~\lambda_3 > 0$, satisfying

\[\left[{\begin{array}{*{20}{c}} {{{\tilde A}^{\rm{T}}}\tilde P + \tilde P\tilde A + \theta \tilde P - {\lambda _1}{Q_y} - {\lambda _2}{Q_w}}& * \\ {{{\tilde H}^{\rm{T}}}\tilde P}&{ - \iota I} \end{array}} \right]\underline \prec 0, \]

(22)

\[{\tilde B^{\rm{T}}}\tilde P\tilde B - \tilde P + {\lambda _3}{Q_y}\underline \prec 0, \]

(23)

\[{\tilde B^{\rm{T}}}\tilde P\tilde B - \tilde P + {\lambda _3}{Q_w}\underline \prec 0, \]

(24)

\[\left[{\begin{array}{*{20}{c}} {\theta \tilde P}&*&*\\ 0&{({\kappa ^2} - \iota )I}&*\\ {{C_z}}&{{D_z}}&I \end{array}} \right]\underline \succ 0.\]

(25)

Then,

\begin{align} \mathcal{S} = \left\{ \chi \in \mathcal{S}_F \lor \mathcal{S}_J ~\Big|~ \chi^{\rm T} \tilde{P} \chi \leq \frac{\lambda_1 \epsilon + \lambda_2 \delta}{\theta} \right\} \end{align}

(26)

is a globally asymptotically stable set for (10) with $\omega = 0$. Moreover, the $\mathcal{L}_\infty$-gain of (10) is smaller than or equal to $\kappa$ and $\delta(\chi(0))$ in (21) can be taken as $\delta(\chi(0)) = (\theta\chi^{\rm T}(0)\tilde{P}\chi(0) + \lambda_1\epsilon + \lambda_2\delta)^{1/2}$.

$\textbf{Proof.}$ Define $V(\chi)=\chi^{\rm T} \tilde{P} \chi$, then we have $\dot{V}(\chi)=\dot{\chi}^{\rm T} \tilde{P} \chi + \chi^{\rm T} \tilde{P} \dot{\chi}$. Using (22)-(24), it can be rewritten as

\begin{align*} \dot{V}(\chi) \le -\theta V(\chi)+\lambda_1\epsilon+\lambda_2\delta + \iota\|\omega\|^2, t \in (t_k, t_{k+1}]. \end{align*}

Using the Comparison Lemma, we can observe that the inequality above implies that

\begin{align} &V(\chi(t)) \leq {\rm e}^{-\theta(t-t_k)} V(\chi^+(t_k)) + \int^{T}_{t_k} {\rm e}^{-\theta(t-s)} \big( \iota\|\omega(s)\|^2 \nonumber \\ & \qquad +\lambda_1\epsilon + \lambda_2\delta \big){\rm d}s, ~t \in (t_k, t_{k+1}], ~k \in {\bf N}. \end{align}

(27)

From (23) and (24), we can get

\begin{align*} &V(\tilde{B}\chi)-V(\chi)\le -\lambda_3\epsilon, \\ &V(\tilde{B}\chi)-V(\chi)\le -\lambda_3\delta. \end{align*}

Using $V(\tilde{B}\chi)-V(\chi)\le 0$ and (27) repeatedly, and the fact that $\{ t_k | k \in {\bf N} \}$ does not have accumulation points, we obtain that

\begin{align} &V(\chi(t)) \leq {\rm e}^{-\theta t} V(\chi(0)) + \int^{T}_0 {\rm e}^{-\theta(t-s)} \big( \iota \|\omega(s)\|^2 \nonumber \\ &\qquad +\lambda_1\epsilon + \lambda_2\delta \big){\rm d}s, ~t \in {\bf R}^+. \nonumber \end{align}

And thus,

\begin{align} V(\chi(t)) \leq {\rm e}^{-\theta t} V(\chi(0)) + \frac{\lambda_1\epsilon + \lambda_2\delta}{\theta} + \frac{\iota}{\theta} \|\omega\|^2_{\mathcal{L}_\infty}. \end{align}

(28)

Observe that (25) implies that

\begin{align} \|z_p(t)\|^2 \leq \theta V(\chi(t)) + (\kappa^2 - \iota) \|\omega(t)\|^2, \end{align}

(29)

and that $\kappa^2 \ge \iota$. We substitute (28) into (29) and observe that $\|\omega(t)\| \le \|\omega\|_{\mathcal{L}_\infty}$ for all $t \in {\bf R}^+$, yielding

\begin{align} \|z_p(t)\|^2 \le \theta {\rm e}^{-\theta t} V(\chi(0)) + \lambda_1\epsilon + \lambda_2\delta + \kappa^2\|\omega\|^2_{\mathcal{L}_\infty}, t \in {\bf R}^+. \end{align}

(30)

Taking now the supremum of the left and the right-hand side of (30) over all time $t \in {\bf R}^+$, we have that

\[\parallel {z_p}\parallel _{{{\cal L}_\infty }}^2 \le \delta {(\chi (0))^2} + {\kappa ^2}\parallel \omega \parallel _{{{\cal L}_\infty }}^2 \le {(\delta (\chi (0)) + \kappa \parallel \omega {\parallel _{{{\cal L}_\infty }}})^2}\]

with $\delta(\chi(0))$ as defined in the hypothesis of the theorem. This shows that the $\mathcal{L}_\infty$-gain is smaller than $\kappa$.

$\square$

As a specific example, let us consider the case in which the disturbance equals zero, that is $\omega = 0$. Therefore, we can obtain the next corollary.

${\bf Corollary 1.}$ Consider the event-triggered control system given by (10), with (11), (13), (15) and (16) and assume its solutions exist for all $t \in {\bf R}^+$. Moreover, suppose there exist a positive definite matrix $P_x \in {\bf R}^{(n_x+n_z+n_e) \times (n_x+n_z+n_e)}$, a positive semidefinite matrix $P_\chi \in {\bf R}^{n_\chi \times n_\chi}$, and $\tilde{P}:={\rm diag}\{P_x, 0\}+P_\chi$, scalars $\theta >0, \lambda_1>0, \lambda_2>0, \lambda_3>0$, satisfying

\[{{\tilde A}^{\rm{T}}}\tilde P + \tilde P\tilde A + \theta \tilde P - {\lambda _1}{Q_y} - {\lambda _2}{Q_w}\underline \prec 0, \]

(31)

\[{{\tilde B}^{\rm{T}}}\tilde P\tilde B - \tilde P + {\lambda _3}{Q_y}\underline \prec 0, \]

(32)

\[{{\tilde B}^{\rm{T}}}\tilde P\tilde B - \tilde P + {\lambda _3}, {Q_w}\underline \prec 0, \]

(33)

then, $\mathcal{S}=\{\chi \in \mathcal{S}_F \lor \mathcal{S}_J~|~\chi^{\rm T} \tilde{P}\chi \le \frac{\lambda_1 \epsilon + \lambda_2 \delta}{\theta}\}$ is a globally asymptotically stable set for the system (10).

${\bf Remark 1.}$ In Theorem 1, we assume that there exists a minimum inter-event time $\tau>0$, and its proof is given in the next theorem. From the expression of $\mathcal{S}$ we can see that $\epsilon$ and $\delta$ are parameters influencing the asymptotically stable set. Small $\epsilon$ and $\delta$ will lead to better performance, with the cost of stricter event-triggered mechanism and more transmissions.

${\bf Theorem 2.}$ Consider the event-triggered control system (10), with (11), (12), (13), (15), (16) and (20). For every initial condition $\chi(0)$ satisfying $\|\chi(0)\| \le a$ and every disturbance $\omega \in {\bf R}^r$ satisfying $\|\omega\| \le b$, there exists a nonzero minimum inter-event time $\tau$, i.e., $t_{k+1}-t_k \ge \tau > 0$, for all $k \in {\bf N}$. An explicit expression for a lower bound on $\tau$ is given by

\begin{align} \min \bigg\{ \tau > 0 \Big| \lambda_{\max} \Big( \Big[ \begin{array}{c} I\\0 \end{array} \Big]^{\rm T} {\rm e}^{\tilde{A}^{\rm T} \tau} Q_y {\rm e}^{\tilde{A} \tau} \Big[\begin{array}{c} I\\0 \end{array} \Big] \Big) \ge \frac{\zeta_y(\tau)}{\xi} \nonumber \\ \textrm{or} \quad \lambda_{\max} \Big( \Big[\begin{array}{c} I\\0 \end{array} \Big]^{\rm T} {\rm e}^{\tilde{A}^{\rm T} \tau} Q_w {\rm e}^{\tilde{A} \tau} \Big[\begin{array}{c} I\\0 \end{array} \Big] \Big) \ge \frac{\zeta_w(\tau)}{\xi} \bigg\}, \end{align}

(34)

in which

\[{\zeta _y}(\tau ) = - \parallel {Q_y}\parallel (\rho (\tau ) + 2\sqrt {\xi \rho (\tau )} \parallel {{\rm{e}}^{\tilde A\tau }}\tilde B\parallel ), \]

(35)

\[{\zeta _w}(\tau ) = \delta - \parallel {Q_w}\parallel (\rho (\tau ) + 2\sqrt {\xi \rho (\tau )} \parallel {{\rm{e}}^{\tilde A\tau }}\tilde B\parallel ), \]

(36)

\[\xi = \frac{{{\lambda _{\max }}(\tilde P)\theta {a^2} + \iota {b^2} + {\lambda _1} + {\lambda _2}\delta }}{{\theta {\lambda _{\min }}({P_x})}}, \]

(37)

\[\rho (\tau ) = \tau \int_0^\tau {{{\rm{e}}^{{\lambda _{\max }}({{\tilde A}^{\rm{T}}} + \tilde A)s}}} {\rm{d}}s\parallel \tilde H{\parallel ^2}{b^2}.\]

(38)

$\textbf{Proof.}$ In the proof of this theorem, we will temporarily introduce notations $Q_i, \zeta_i$ and $\epsilon_i$, in which $i = y, w$. That means $\epsilon_y = \epsilon$ and $\epsilon_w = \delta$. At the start of computing a guaranteed $\tau > 0$, we compute the event time $t_{k+1}$ given by (8), which can be expressed as

\[{t_{k + 1}} = \inf \left\{ {t > {t_k}\left| {{{\left[ {\begin{array}{*{20}{c}} {{\chi _x}}\\ {{\chi _e}} \end{array}} \right]}^{\rm{T}}}{Q_i}\left[ {\begin{array}{*{20}{c}} {{\chi _x}}\\ {{\chi _e}} \end{array}} \right] = \epsilon_i} \right.} \right\}.\]

Solving the differential equation $\dot{\chi} = \tilde{A}\chi + \tilde{H}\omega$, we can get the solution

\[\chi = {{\rm{e}}^{\tilde A(t - {t_k})}}\chi ({t_k}) + \int_{{t_k}}^T {{{\rm{e}}^{\tilde A(t - s)}}} \tilde H\omega (s){\rm{d}}s.\]

Substitute it into $\chi^{\rm T} Q_i \chi < \epsilon_i$, yielding

\begin{align} &\Big({\rm e}^{\tilde{A}(t-t_k)}\chi(t_k) + \int^{T}_{t_k} {\rm e}^{\tilde{A}(t-s)}\tilde{H}\omega(s){\rm d}s \Big)^{\rm T} Q_i \nonumber \\ &\qquad \times \Big({\rm e}^{\tilde{A}(t-t_k)}\chi(t_k) + \int^{T}_{t_k} {\rm e}^{\tilde{A}(t-s)}\tilde{H}\omega(s){\rm d}s \Big) < \epsilon_i, \end{align}

(39)

which is equivalent to

\begin{align} &\chi^{\rm T}(t_k) {\rm e}^{\tilde{A}^{\rm T}(t-t_k)} Q_i {\rm e}^{\tilde{A}(t-t_k)} \chi(t_k) \nonumber \\ &\qquad +\int^{ T}_{t_k} \big( \tilde{H}\omega(s) \big)^{\rm T} {\rm e}^{\tilde{A}^{\rm T}(t-s)}{\rm d}s Q_i \int^{T}_{t_k} {\rm e}^{\tilde{A}(t-s)}\tilde{H}\omega(s){\rm d}s \nonumber \\ &\qquad +2{\rm e}^{\tilde{A}(t-t_k)}\chi(t_k) Q_i \int^{ T}_{t_k} \big( \tilde{H}\omega(s) \big)^{\rm T} {\rm e}^{\tilde{A}^{\rm T}(t-s)}{\rm d}s < \epsilon_i. \end{align}

(40)

Now using Holder's inequality and Wazewski's inequality, we can get

\begin{align} &\|\int^{T}_{t_k} {\rm e}^{\tilde{A}(t-s)} \tilde{H}\omega(s){\rm d}s\|^2 \nonumber \\ &\qquad \le\int^{T}_{t_k} {\rm e}^{\lambda_{\max}(\tilde{A}^{\rm T}+\tilde{A})(t-s)}{\rm d}s \int^{T}_{t_k} \|\tilde{H}\omega(s)\|^2 {\rm d}s \nonumber \\ &\qquad \le\int^{t-t_k}_0 {\rm e}^{\lambda_{\max}(\tilde{A}^{\rm T}+\tilde{A})s} {\rm d}s \int^{T}_{t_k}1{\rm d}s\nonumber \\ & \qquad \times \sup_{s \in (t_k, t]} \|\tilde{H}\omega(s)\|^2. \end{align}

(41)

Hence, the left-hand side of (41) can be upper bounded by $\rho(t-t_k)$, with $\rho(\cdot)$ defined in (38). Therefore,

\begin{align} & \chi^{\rm T}_x(t_k) \Big[\begin{array}{c} I\\0 \end{array} \Big]^{\rm T} {\rm e}^{\tilde{A}^{\rm T}(t-t_k)} Q_i {\rm e}^{\tilde{A}(t-t_k)} \Big[\begin{array}{c} I\\0 \end{array} \Big] \chi_x(t_k) \nonumber \\ &\qquad <\zeta_i(t-t_k), \end{align}

(42)

for $t > t_k$, implying satisfaction of (40). Namely, no events are triggered as long as (42) is satisfied. From (28) in Theorem 1, we can get

\begin{align*} V(\chi(t)) \le \lambda_{\max}(\tilde{P}) \|\chi(0)\|^2 + \frac{\lambda_1\epsilon + \lambda_2\delta}{\theta} + \frac{\iota}{\theta} \|\omega\|^2_{\mathcal{L}_\infty}. \end{align*}

Hence,

\begin{align} &\|\chi_x(t)\|^2 \le\frac{1}{\lambda_{\min}(P_x)} \big( \chi^{\rm T}_x P_x \chi_x + \chi^{\rm T} P_\chi \chi \big) \nonumber \\ &\qquad =\frac{1}{\lambda_{\min}(P_x)} V(\chi(t))\le \xi. \end{align}

(43)

Now the solution to (34) is the smallest value $\tau_{\min}:=t-t_k$, such that

\begin{align} \chi^{\rm T}_x \Big[\begin{array}{c} I\\0 \end{array} \Big]^{\rm T} {\rm e}^{\tilde{A}^{\rm T} \tau_{\min}} Q_i {\rm e}^{\tilde{A} \tau_{\min}} \Big[ \begin{array}{c} I\\0 \end{array} \Big] \chi_x = \frac{\zeta_i(\tau_{\min}) \|\chi_x\|^2}{\xi}. \end{align}

(44)

Thus, by using equations (43), (44), we can get the conclusion that (42) is satisfied as long as $t < t_k + \tau_{\min}$, or equivalently, no events are triggered under these conditions.

$\square$

${\bf Theorem 3.}$ Consider the event-triggered control system given by (10), with (11), (13), (15) and (16). For every initial condition $\chi(0)$ satisfying $\|\chi(0)\|\le a$, there exists a time $\tau \in {\bf R}^+$ such that the inter-event time implicitly defined by the event-triggering mechanism (8) are lower bounded by $\tau$, i.e., $t_{k+1}-t_k\ge \tau > 0$, for all $k\in {\bf N}$. And the lower bound can be described as

\begin{align} \min\bigg\{\tau >0\bigg| \lambda_{\rm max} \bigg(\left[\begin{array}{l}I\\0 \end{array}\right]^{\rm T} {\rm e}^{\tilde{A}^{\rm T}\tau}Q_y {\rm e}^{\tilde{A}\tau}\left[\begin{array}{l}I\\0 \end{array}\right]\bigg) \ge\frac{\epsilon}{\xi} \nonumber\\ \textrm{or} \quad \lambda_{\rm max} \bigg(\left[\begin{array}{l}I\\0 \end{array}\right]^{\rm T} {\rm e}^{\tilde{A}^{\rm T}\tau}Q_y {\rm e}^{\tilde{A}\tau}\left[\begin{array}{l}I\\0 \end{array}\right]\bigg)\ge\frac{\epsilon}{\xi}\bigg\}, \end{align}

(45)

where

\begin{align} \xi=\frac{\lambda_{\rm max}(\tilde{P})\theta a^2 + \lambda_1 \epsilon+\lambda_2\delta}{\theta\lambda_{\rm min}(P_x)}, \end{align}

(46)

with $\tilde{P}$ and $P_x$ defined in Theorem 1.

$\textbf{Proof.}$ By Theorem 1, we know that

\begin{align} \dot{V}(\chi) \le -\theta V(\chi)+\lambda_1\epsilon+\lambda_2\delta \end{align}

(47)

holds for $t \in (t_k, t_{k+1}]$, $k \in {\bf N}$. Using comparison lemma, we have

\begin{align} &V(\chi)\le {\rm e}^{-\theta (t-t_k)}V(\chi^+(t_k)) \nonumber\\ &\qquad +\int_{t_k}^{T}{\rm e}^{-\theta(t-\rho)}(\lambda_1\epsilon+\lambda_2\delta){\rm d}\rho, \end{align}

(48)

$t \in (t_k, t_{k+1}]$, $k \in {\bf N}$. Using (47) and (48) iteratively, we obtain $V(\chi)\le {\rm e}^{-\theta t}V(\chi(0))+\int_0^{T} {\rm e}^{-\theta(t-\rho)}(\lambda_1\epsilon+\lambda_2\delta){\rm d}\rho$, thus, we have

\begin{align} &V(\chi)\le {\rm e}^{-\theta t}V(\chi (0))+\frac{\lambda_1\epsilon+\lambda_2\delta}{\theta} \nonumber \\ &\qquad \le\lambda_{\rm max}(\tilde{P}) \|\chi(0)\|^2+\frac{\lambda_1\epsilon+\lambda_2\delta}{\theta} \nonumber \\ &\qquad \le\lambda_{\rm max}(\tilde{P})a^2+\frac{\lambda_1\epsilon+\lambda_2\delta}{\theta}. \end{align}

(49)

Notice that,

\[V(\chi ) = {\chi ^{\rm{T}}}\tilde P\chi = \chi _x^{\rm{T}}{P_x}{\chi _x} + {\chi ^{\rm{T}}}{P_\chi }\chi \ge {\lambda _{{\rm{min}}}}({P_x})\chi _x^{\rm{T}}{\chi _x}, \]

therefore

\begin{align} \|\chi_x\|^2 \le \xi. \end{align}

(50)

Solving the differential equation $\dot{\chi}=\tilde{A}\chi$ from $t_k$ to $t>t_k$, we get $\chi={\rm e}^{\tilde{A}(t-t_k)}\chi^+(t_k)={\rm e}^{\tilde{A}(t-t_k)}\left[\begin{array}{l} I\\0\end{array}\right]\chi_x(t_k)$. From (15) we know that, as long as $t\ge t_k$ satisfies

\begin{align*} \bigg \{\chi_x^{\rm T}(t_k) \left[\begin{array}{l}I\\0\end{array} \right]^{\rm T} {\rm e}^{\tilde{A}^{\rm T}(t-t_k)} Q_y {\rm e}^{\tilde{A}(t-t_k)} \left[\begin{array}{l}I\\0\end{array} \right] \chi_x(t_k) < \epsilon \nonumber\\ \end{align*}

and

\[\chi _x^{\rm{T}}({t_k}){\left[{\begin{array}{*{20}{l}} I\\ 0 \end{array}} \right]^{\rm{T}}}{{\rm{e}}^{{{\tilde A}^{\rm{T}}}(t - {t_k})}}{Q_w}{{\rm{e}}^{\tilde A(t - {t_k})}}\left[{\begin{array}{*{20}{l}} I\\ 0 \end{array}} \right]{\chi _x}({t_k}) < \delta \} , \]

no events are triggered. We know that $\tau$ is the smallest value satisfying (45), which is equivalent to

\begin{align} \bigg \{\left[\begin{array}{l}I\\0 \end{array}\right]^{\rm T} {\rm e}^{\tilde{A}^{\rm T}\tau}Q_y {\rm e}^{\tilde{A}\tau} \left[\begin{array}{l}I\\0 \end{array}\right]-\frac{\epsilon}{\xi}I \nprec 0 \quad\nonumber\\ \textrm{or} ~~\left[\begin{array}{l}I\\0 \end{array}\right]^{\rm T} {\rm e}^{\tilde{A}^{\rm T}\tau}Q_w {\rm e}^{\tilde{A}\tau}\left[\begin{array}{l}I\\0 \end{array}\right]-\frac{\delta}{\xi}I \nprec 0 \bigg \}, \end{align}

(51)

hence, for $t_k < t < t_k + \tau$,

\[\{ {\left[{\begin{array}{*{20}{l}} I\\ 0 \end{array}} \right]^{\rm{T}}}{{\rm{e}}^{{{\tilde A}^{\rm{T}}}(t - {t_k})}}{Q_y}{{\rm{e}}^{\tilde A(t - {t_k})}}\left[{\begin{array}{*{20}{l}} I\\ 0 \end{array}} \right] \prec \frac{}{\xi }I\]

and

\[{\left[{\begin{array}{*{20}{l}} I\\ 0 \end{array}} \right]^{\rm{T}}}{{\rm{e}}^{{{\tilde A}^{\rm{T}}}(t - {t_k})}}{Q_w}{{\rm{e}}^{\tilde A(t - {t_k})}}\left[{\begin{array}{*{20}{l}} I\\ 0 \end{array}} \right] \prec \frac{\delta }{\xi }I\} .\]

(52)

This together with (50) implies

\begin{align} &\chi_x^{\rm T}(t_k)\left[\begin{array}{l}I\\0 \end{array}\right]^{\rm T} {\rm e}^{\tilde{A}^{\rm T} (t-t_k)} Q_y {\rm e}^{\tilde{A} (t-t_k)}\left[\begin{array}{l}I\\0 \end{array}\right]\chi_x(t_k) \nonumber\\ &\qquad <\chi_x^{\rm T}(t_k) \frac{\epsilon}{\xi} \chi_x(t_k) < \frac{\epsilon}{\xi} \xi = \epsilon \end{align}

(53)

and

\begin{align} &\chi_x^{\rm T}(t_k)\left[\begin{array}{l}I\\0 \end{array}\right]^{\rm T} {\rm e}^{\tilde{A}^{\rm T} (t-t_k)}Q_w {\rm e}^{\tilde{A} (t-t_k))}\left[\begin{array}{l}I\\0 \end{array}\right]\chi_x(t_k) \nonumber \\ &\qquad <\chi_x^{\rm T}(t_k) \frac{\delta}{\xi} \chi_x(t_k) < \frac{\delta}{\xi}\xi=\delta. \end{align}

(54)

Hence, we have that (15) is guaranteed to be satisfied and thus no events are triggered under these conditions. This provides a lower bound on the inter-event time.

$\square$

B. Interpreting the Event-induced Error as a Disturbance

The purpose of this subsection is to show that the methods proposed in ^[16] for the case of state observers can be generalized to a function observer scenario. We begin by briefly introducing the principle (further details may be found in the corresponding references) and then proceed to describe their stability properties when the control input directly uses the sampled value of the output $Kx$ of the function observer.

It is shown in ^[16] that if the typical event is defined as the error signals exceeding a given threshold, and the observer along with controller are updated only at the event-triggered sampling instants, then the closed-loop system is globally uniformly ultimately bounded stable.

We present a procedure by considering the group of $\hat{e}$ and $\tilde{e}$ as an external disturbance. As for the event-triggered mechanism (8), we set $\sigma = 0, \: \zeta = 0$, and then get $t_{k+1}=\inf \{ t>t_k |~\| \hat{e}(t) \| = \sqrt{\epsilon} \; \textrm{or} \; \| \tilde{e} \| = \sqrt{\delta} \}$. Define $\bar{x}=[x^{\rm T}~z^{\rm T}~e^{\rm T}]^{\rm T}$, $\bar{e}=[\hat{e}^{\rm T}~\tilde{e}^{\rm T}]^{\rm T}$ and $\gamma = \epsilon + \delta$, then the event-triggered mechanism can be replaced by a more conservative condition $t_{k+1}=\inf \{ t>t_k |~\|\overline{e}(t)\| = \sqrt{\gamma}~\}$.

In this subsection, we assume the practical external disturbance is equal to zero, i.e., $\omega =0$. Thus the closed-loop system (9) can be written as

\begin{align} \dot{\bar{x}}=\bar{A}\bar{x}+\bar{B}\bar{e}, ~t\in [t_k, t_{k+1}), \end{align}

(55)

\begin{align} \dot{\bar{x}}=\bar{A}\bar{x}+\bar{B}\bar{e}, ~t\in [t_k, t_{k+1}), \end{align} where

\[\bar A = \left[{\begin{array}{*{20}{c}} {A + BMC}&{BE}&0\\ {(NM + G)C}&{F + NE}&0\\ 0&0&F \end{array}} \right], \]

(56)

\[\bar B = \left[{\begin{array}{*{20}{c}} {BM}&B\\ {NM + G}&N\\ { - G}&0 \end{array}} \right].\]

(57)

We have the following theorem.

${\bf Theorem 4.}$ Consider the closed-loop system (55) with event-triggered mechanism determined by

\begin{align} t_{k+1}=\inf \{ t>t_k |~\|\overline{e}(t)\| = \sqrt{\gamma}~\}, ~{\rm for~all}~k\in {\bf N}. \end{align}

(58)

If there exists a positive matrix $\bar{P}$ satisfying $\bar{A}^{\rm T}\bar{P}+\bar{P}\bar{A}+\bar{P}\bar{B}\bar{B}^{\rm T}\bar{P}=P_N \prec 0$, then the closed-loop system (55) is globally uniformly ultimately bounded stable and its state exponentially converges to the bounded region

\[{\cal R}(\gamma ) = \{ \bar x(t)|\parallel \bar x\parallel \le \sqrt {\frac{{{\lambda _{{\rm{max}}}}(\bar P)\gamma }}{{(1 - {{\rm{e}}^{ - \nu {t_{{\rm{min}}}}}}){\lambda _{{\rm{min}}}}(\bar P){\lambda _{{\rm{min}}}}( - {P_N})}}} \} \]

where $\nu = \frac{\lambda_{\rm min}(-P_N)}{\lambda_{\rm max}(\bar{P})}$, and $t_{\rm min}=\inf_{k \in {\bf N}} \{ t_{k+1}-t_k \}$.

$\textbf{Proof.}$ The proof line used here consults the proof of Theorem 1 in ^[16]. Take a Lyapunov function $V(t)=\bar{x}^{\rm T}\bar{P}\bar{x}$, then we can get

\begin{align} \dot{V}(t) &=& \dot{\bar{x}}^{\rm T}\bar{P}\bar{x}+\bar{x}^{\rm T}\bar{P}\dot{\bar{x}} \le -\lambda_{\rm min}(-P_N) \| \bar{x} \|^2+ \| \bar{e} \| ^2.\nonumber \end{align}

Besides, from (58) we have that $ \| \bar{e} \| \le \sqrt{\gamma}$. Hence, after some calculations we obtain $\dot{V} \le -\kappa V+\gamma$. Moreover, multiplying ${\rm e}^{\kappa(t-t_k)}$ on both sides of the above inequality and taking several equivalence transformations lead to \\ $ \| \bar{x} \|^2 \le {\rm e}^{-\kappa(t-t_k)} \frac{\lambda_{\rm max}(\bar{P})}{\lambda_{{\rm min}(\bar{P})}} \| \bar{x}(t_k) \|^2 + \frac{\lambda_{\rm max}(\bar{P})\gamma}{\lambda_{\rm min}(\bar{P})\lambda_{\rm min}(-P_N)}$ which implies that in every time interval $[t_k, t_{k+1})$, $\bar{x}$ decays exponentially. If we repeat the computation, then we have $V(t) \le {\rm e}^{-\kappa(t-t_0)}V(t_0)+\frac{\gamma}{\kappa(1-{\rm e}^{-\kappa t_{\rm min}})}$, proving thus the claim.

\square$

V. NUMERICAL EXAMPLE

In this section, we borrow the ball and beam model from ^[18], %\cite{Velasco_2008}, with state space description

\begin{align*} \dot{x}= \left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array} \right] x+ \left[\begin{array}{l} 0 \\ 1 \end{array} \right] u, \quad y=[1~~0]x. \end{align*}

A feedback gain placing the poles of the closed loop system at $\{ -1+1j, -1-1j\}$ is given by $K\!\!=\!\![-2~-2]$. Select $F \!\!=\!\! \left[\begin{array}{cc} -0.4 & 0 \\0 & -0.7 \end{array} \right]$ satisfying that all its eigenvalues in the left-half complex plane are different from the eigenvalues of $A$. Select $G= \left[ \begin{array}{l} 1 \\ 1 \end{array} \right]$, and then we can get $P\!\!=\!\!\left[\begin{array}{cc} 2.5000 & -6.2500\\ 1.4286 & -2.0408 \end{array} \right]$ by solving $PA-FP=GC$; Moreover, $N=\left[\begin{array}{l} -6.2500 \\ -2.0408 \end{array} \right]$, $E=[2.3467~-6.2067]$, and $M=1$ satisfying $N=PB, ~ K=EP+MC$.

A. Hybrid Dynamical Systems Method with Disturbance

The initial condition is set to be $x_0=[-0.1~~0.2]^{\rm T}$. Besides, the disturbance is chosen as white noise, with mean equal to zero and variance equal to one.

With event-triggered mechanism (8), by solving the LMIs (22)-(25), we get a feasible value $\sigma = \zeta =0.001$. If we take $\epsilon = \delta =0.005$, then practical stability of the event-triggered control system (3), (5) can be guaranteed using the hybrid system formulation.

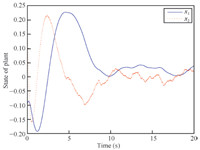
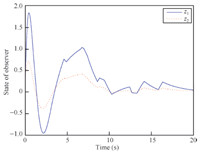
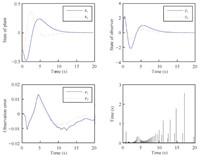
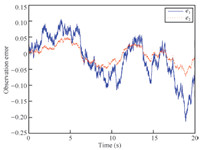
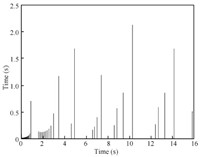
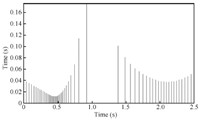
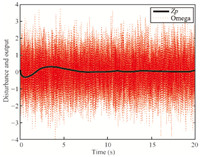
The evolution of the plant state and the function observer state as a function of time are illustrated in Figs. 2 and 3. Moreover, the plots depicted in Fig. 4 show the behavior of the observation error. The evolution of the inter-event time is shown in Fig. 5. In Fig. 6, we can observe that the performance output $z_p$ is relatively good with $L_\infty$-gain $\kappa = 0.0739$.

We can see that the system converges gently, requiring a period of time of about $10, {\rm s}$. During this time, the sampling is executed frequently and the minimum inter-event time is $0.0180, {\rm s}$. When $t > 10, {\rm s}$, all the trajectories of the plant and the observer are bounded to an area around the zero equilibrium. And this means asymptotic stability of a compact set. Besides, the average task period is $0.3255, {\rm s}$. what is important to note here is the continuous slight fluctuation of the observation error, as is shown in Fig. 4. This suggests there should be a persistent disturbance imposed on the system. To some extent, this method provides a first step at developing hybrid-system-based event-triggered mechanism when there is disturbance. With the findings from this simulation in hand, one can identify an important issue that future research into observer-based event-triggered control with persistent disturbance may confront. And one might, for instance, implement an event-triggered disturbance decoupled observer.

B. Hybrid Dynamical Systems Method Without Disturbance

The initial condition is chosen as $x_0=[-0.3~~0.2]^{\rm T}$. Besides, the disturbance is set to be zero.

With event-triggered mechanism (8), by solving the LMIs (31)-(33), we get a feasible value $\sigma = \zeta =0.019$. If we take $\epsilon = \delta =0.001$, then practical stability of the event-triggered control system (3), (4) can be guaranteed using the hybrid system formulation.

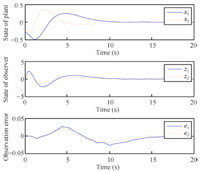
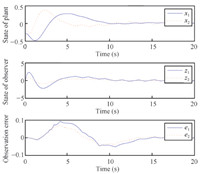
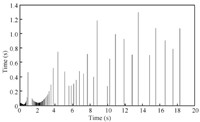
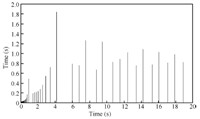
The evolution of the plant state, function observer state and observation error as a function of time are illustrated in Fig. 7. The evolution of the inter-event time is shown in Fig. 8. To more clearly illustrate the samples, Fig. 9 presents the zoom-in version of the first two seconds.

We can see that the system converges gently, requiring a period of time of about $10, {\rm s}$. During this time, the sampling is executed frequently as the observation error is relatively large and the minimum inter-event time is $0.0120, {\rm s}$. When $t > 10, {\rm s}$, all the trajectories of the plant and the observer are bounded to an area around the zero equilibrium. And this means asymptotic stability of a compact set. Besides, the average task period is $0.2061, {\rm s}$.

Comparing both Figs. 7 and 8, we notice that samplings occur less often when the system is close to its steady state, although there are slight fluctuations of the plant and observer state. This also demonstrates the tradeoff between the number of samples and system performance.

Taking $\epsilon=\delta=0.0001$, we will get Fig. 10. The minimum inter-event time is $0.0040, {\rm s}$ and average task period is $0.1234, {\rm s}$. Interestingly, for a smaller $\epsilon$ and $\delta$, the fluctuations of the plant state when $t>10, {\rm s}$ also become smaller, given by $0.2524, \%$. Whereas this is $0.6427, \%$ if we take $\epsilon=\delta=0.001$. However, the number of transmissions that are needed is $161$ with $\epsilon=\delta=0.0001$ and only $94$ with $\epsilon=\delta=0.001$, which is a reduction of $41.61\%$. This fact is in accordance with Remark 2.

From these results, we can formally prove that a globally asymptotically stable compact set does exist and the minimum inter-event time is positive. Furthermore, we can conclude that hybrid dynamical system method truly describes the dynamic characteristics of the event-triggered control system.

C. Interpreting the Event-induced Error as a Disturbance

Taking $\gamma = 0.02$, the event-triggered condition is $t_{k+1}= \inf \{ t>t_k | ~\| \bar{e}(t) \|^2>0.02\}$, then it can be verified that conditions in Theorem 4 are satisfied. The state trajectories in Fig. 11 demonstrate the ultimately bounded stability of the system.

The inter-event time illustrated in Fig. 12 have an average value of $0.4376, {\rm s}$. The guaranteed minimum inter-event time is $0.0200, {\rm s}$. We observe that samples are executed significantly frequently at the first second. And indeed $46.67, \%$ of them take place when $t<0.9030, {\rm s}$.

VI. CONCLUSION

In this paper, the issue of event-triggered control based on function observer was explored. An event-triggering mechanism was proposed. To analyze the resulting event-triggered control systems, we used two methods, that is, reformulating it as a hybrid dynamical system and interpreting the event-induced error as disturbance. Conditions of the two methods in terms of matrix inequality were established to guarantee the asymptotic stability of a compact set and ultimately bounded stability, respectively. A numerical example was worked out to show the feasibility of the proposed event-triggered mechanism.