2. the Key Laboratory of Autonomous Systems and Networked Control, Ministry of Education, South China University of Technology, Guangzhou 510640, China;
3. the Key Laboratory of Surface Functional Structure Manufacturing of Guangdong Higher Education Institutes, School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, China
I. INTRODUCTION
Owing to the fact that real actuator cannot deliver arbitrarily large signals,actuator saturation is generally encountered in engineering practice which may causes large performance degradation,e.g.,lag,limit cycles,overshoot,and even instability of control systems due to the so-called "windup" effects[1]. However,for the sake of simplifying the process of a control law design,especially for nonlinear systems due to their inherent complexity,actuator saturation is usually neglected which may cause serious damages and accidents. To mitigate the "windup" effects caused by saturation,a well-established two-step anti-windup approach suggests designing the (linear or nonlinear) dynamic controller a priori and then augmenting it by an anti-windup compensator which only operates when saturation occurs[1, 2, 3, 4, 5, 6, 7]. Two-step approach is considered attractive in practice because the dynamic controller is designed without consideration of actuator saturation. However,this may restrict the improvement of closed-loop performance. In order to pursue better improvement of closed-loop performance during the windup, simultaneously design methods of linear controller and static anti-windup compensator are proposed for saturated linear systems in [8, 9]. Since the knowledge of actuator saturation is incorporated in the design of a linear controller,this approach generally leads to the best closed-loop performance.
Although the vast majority of the anti-windup literature has concentrated on the saturated linear systems,the investigation of anti-windup techniques for nonlinear systems subject to actuator saturation has been constantly focused by the research community[1]. We can cite,for instance,[10, 11] which consider anti-windup synthesis problems for LPV systems[12]; which proposes an adaptive control scheme[13, 14]; which consider anti-windup synthesis problems for rational systems based on differential algebraic representation (DAR) and linear-fractional representation (LFR) techniques,respectively[15, 16, 17]; in which the decoupled-architecture-based anti-windup techniques are proposed for affine nonlinear systems[18]; which proposes a dynamic anti-windup scheme for a class of feedback linearizable systems with nonlinear dynamic inversion (NDI) controllers. The intention of most of the enumerated literatures is the extension of anti-windup techniques for linear systems. In order to construct an anti-windup compensator,LMI-based synthesis conditions need to be solved which generally cause conservatism due to the inherent complexity of nonlinear systems. Hence,how to reduce the conservatism when estimating the ROA becomes one of the most important issues.
A particular type of nonlinear systems which has been gaining great attention for several decades is the class of systems which can be represented as a feedback connection of a linear time-invariant (LTI) system and a nonlinear function with certain properties (e.g.,sector-bounded and Lipschitz constraints). Their stability analysis is typically referred to as "absolute stability" which is still of interest in the literature since it is related to many theoretical and practical control problems ([19, 20, 21, 22, 23, 24] and references therein). However,most of them do not consider the actuator saturation. Recently,anti-windup-based dynamic controller synthesis problems are investigated for Lur'e and Lipschitz systems[25, 26]. Asymptotic as well as input-to-output stabilization problems are addressed both in regional and global contexts. More precisely,in [25],Lur'e systems are investigated and the proposed methods can be applied to design simultaneously a nonlinear controller and a static anti-windup compensator; in [26],Lipschitz systems are investigated in which the approaches just allow to synthesize a linear controller. Since the sector-bounded conditions[25] and Lipschitz conditions[26] do not reflect the unique attributes of nonlinearities, the proposed synthesis conditions might cause large conservatism.
In this paper,simultaneous synthesis of dynamic controller and static anti-windup compensator is investigated for Lipschitz systems subject to actuator saturation. Based on the reformulated Lipschitz property[24],the nonlinear systems can be transformed into LPV systems whose system matrices are affine in a parameter matrix. Using the modified sector-bounded condition dealing with actuator saturation,BMI synthesis conditions are proposed which can be solved by the ILMI optimization procedure[27] at the vertices of a given bounded convex set. Since the reformulated Lipschitz property is less conservative than the traditional one,it is expected that the proposed synthesis method would attain better closed-loop performances than the one in [26]. Consider the case that the nonlinearity $\varphi(x)$ globally satisfies both Lipschitz and sector-bounded conditions. Due to more variable matrices existing in the synthesis conditions,the proposed methods could lead to less conservative optimal or suboptimal results.
The paper is organized as follows. In Section II,the problem to be treated is formally stated,and some useful preliminary results are presented. In Section III,a theoretical foundation on anti-windup-based dynamic controller synthesis is developed. In Section IV,a numerical example is presented to illustrate the effectiveness of the proposed method and at last,some remarks conclude the paper.
The notation used in this paper is standard. For any real matrices $A$,$B \in {{\bf R} ^{n \times n}}$,$A^{\rm{T}}$ denotes the transpose of $A$,and $A^{-1}$ is the inverse. $A \geq ({\rm or} >)~0$ means that matrix $A$ is symmetric and positive semi-definite (positive-definite),and $A \geq ({\rm or} >)~ B$ means that matrix $A-B \geq ({\rm or} >)~ 0$. $He\{A\}= A+A^{\rm{T}}$. For a real matrix $P>0$,${\cal E}(P)$ denotes the ellipsoid $\{ {x| {{x^{\rm{T}}}Px \le 1} } \}$. $I$ or $I_n$ denotes the identity matrix. $\tau^n_i$ denotes the $i$th row of $I_n$ (sometimes $n$ is ignored). ${\rm diag}\{A,B\}$ denotes the block-diagonal matrix [A~0;0~B]. For any vector $x,y \in {\bf R}^n$,the Euclidean norm is denoted as $\|x\|$; $x \geq 0$ means that all the components of $x$ (denoted as $x_i$) are nonnegative; $x \geq y$ means that $x_{i}\geq y_{i}$. $|x_i|$ represents the absolute value of $x_i$. The $\mathcal {L}_2$ gain from a signal $w(t)$ to another signal $z(t)$ is represented as ${\sup _{\|w(t)\|_2 \ne 0}}(\|z(t)\|_2/\|w(t)\|_2)$,where $\|\cdot\|_2$ is defined in Section II. For a symmetric block matrix,the symbol "$\star$" stands for the symmetrical block outside the main diagonal.
II. PROBLEM STATEMENT AND PRELIMINARIES
Consider the following nonlinear systems:
| \begin{align} &\dot x = Ax + {B_\varphi }\varphi (x) + {B_u}sat({v_c}) + {B_w}w,\nonumber\\[1mm] &y = {C_y}x + D_{y\varphi}\varphi (x) + {D_{yw}}w,\notag\\[1mm] &z = {C_z}x + {D_{z\varphi }}\varphi (x) + {D_{zu}}sat({v_c}) + {D_{zw}}w, \end{align} | (1) |
$\textbf{A1.}$ For any $X,Y \in\mathcal {B}_\varphi=\{x|,| x_k| \leq \kappa_k,\; k=1,\ldots,n\} \subseteq {\bf R}^r$,the nonlinearity $\varphi(x)$ satisfies: $\varphi(0)=0$ and $\| \varphi(X) - \varphi(Y) \| \le \gamma_{\varphi} \| X-Y \|$ where $\gamma_{\varphi}$ is called the Lipschitz constant.
$\textbf{A2.}$ the exogenous inputs $w(t)$ is bounded in energy,i.e., for some limited scalar $\lambda$,$w(t)$ satisfies:
| \begin{align} \left\| {w(t)} \right\|_2^2= \int\nolimits_0^\infty {w{{(t)}^{\rm{T}}}w(t){\rm d}t} \le \frac{1}{\lambda }.\end{align} | (2) |
Consider the following nonlinear dynamic controller along with the static anti-windup compensator:
| \begin{align} &{{\dot x}_c} = {A_c}{x_c} + {B_{c\varphi }}\varphi (x) + {B_{cu}}y + {E_1}\psi ({v_c}),\nonumber\\[1mm] &{v_c} = {C_c}{x_c} + {D_{c\varphi }}\varphi (x) + {D_{cu}}y + {E_2}\psi ({v_c}),\label{eqq3} \end{align} | (3) |
A. Reformulated Lipschitz Property
Throughout the paper,the following lemma will be useful for deriving LMI-based synthesis conditions.
${\bf Definition 1}[24]. Consider two vectors $X = ( x_1,x_2,\ldots ,$ $x_n)^{\rm{T}}$ and $Y = ( y_1,y_2,\ldots,y_n )^{\rm{T}}$. For all $i=1,\ldots,n$,an auxiliary vector is defined as $X^{Y_i} = (y_1,\ldots,y_i,x_{i + 1},\ldots ,x_n)^{\rm{T}}$. It is also defined that $X^{O_i} = ( 0,\ldots,0,x_{i + 1},\ldots,x_n )^{\rm{T}}$. Particularly,we have ${X^{{Y_0}}} = X$,${X^{{O_n}}} = 0$.
${\bf Lemma 1}[24]. Considering the function $\varphi: {\bf R}^n \rightarrow {\bf R}^r$,the two following items are equivalent:
1) Locally Lipschitz property: $\varphi$ is locally $\gamma_\varphi$-Lipschitz with respect to its argument,i.e.,
| \begin{align} \left\| {\varphi (X) - \varphi (Y)} \right\| \le {\gamma _\varphi }\left\| {X - Y} \right\|,\ \ \forall,X,Y \in {\mathcal {B} _\varphi}.\label{eqq4} \end{align} | (4) |
2) Reformulated Lipschitz property: for all $i=1,\ldots,r$,$j$ $=$ $1,\ldots,n$,there exist functions: $\varphi_{ij}: {\bf R}^n \times {\bf R}^n \rightarrow {\bf R}$ and constants $\underline{\gamma}_{\varphi_{ij}}$ and $\overline{\gamma}_{\varphi_{ij}}$,so that $\forall ,X,Y \in \mathcal {B}_{\varphi} \subseteq {\bf R}^{n}$,
| \begin{align} \varphi(X)-\varphi(Y)=\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^n {{\varphi _{ij}}{H_{ij}}(X - Y)} } \end{align} | (5) |
| \begin{align} \varphi_{ij}= \begin{cases} 0,&{\rm if} ~ x_j=y_j,\\[1mm] \dfrac{\varphi_{i}(X^{Y_{j-1}})-\varphi_{i}(X^{Y_{j}})}{x_j-y_j},& {\rm if} ~ x_j \neq y_j. \end{cases} \end{align} | (6) |
Based on the above Lemma and considering $\varphi(0)=0$,the Lipschitz function $\varphi(x)$ can be represented as:
| \begin{align} \varphi(x)=\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^n {{\varphi _{ij}}{H_{ij}}x} },\ \ \forall ,x \in \mathcal {B}_{\varphi} \subseteq {\bf R}^n, \end{align} | (7) |
| \begin{align} \varphi_{ij}= \begin{cases} 0,&{\rm if} ~x_j=0,\\[1mm] \dfrac{\varphi_{i}(X^{O_{j-1}})-\varphi_{i}(X^{O_{j}})}{x_j},& {\rm if} ~ x_j \neq 0. \end{cases} \end{align} | (8) |
| \begin{align} {{\cal V}_{\cal H}} = \left\{ {\Psi \in {{\bf R} ^{r \times n}}\left| {{\Psi _{ij}} \in \left\{ {{{\underline{\gamma}}_{\varphi _{ij}}},{{\bar \gamma }_{{\varphi _{ij}}}}} \right\}} \right.} \right\}. \label{eqq9}\end{align} | (9) |
Lemma 1 provides a less conservative Lipschitz condition compared to the traditional Lipschitz condition (4). For instance,considering two scalar functions $\varphi(x)={\sin}(x)$ and $\varphi(x)={\tanh}(x)$,the Lipschitz condition (4) does not distinguish between the two nonlinearities. However,with the reformulation (5) and (6),we can see the difference: for $\varphi(x)$ $=$ ${\sin}(x)$,we have $-0.2172\leq\varphi_{11}={{\sin}(x)}/{x}\leq1$; for $\varphi(x)$ $=$ ${\tanh}(x)$,we have $0\leq\varphi_{11}={{\tanh}(x)}/{x}\leq1$.
$\textbf{Corollary~1.}$ Consider a global Lipschitz scalar function $\varphi(x)$ (with $\varphi(0)=0$) which globally satisfies sector-bounded condition:
| \[(\varphi (x) - {K_1}x)(\varphi (x) - {K_2}x) \le 0,\] |
1) $(\varphi (x) - {K_1}x)(\varphi (x) - {K_0}x) \le 0$;
2) $\Theta$ belongs to a bounded convex set $\mathcal {H}$ for which the set of vertices is defined by ${\mathcal {V}_H} = \{ {\Psi \in {\bf R} | {\Psi \in \{ {{K_1},\;{K_0}} \}}} \}$. Particularly,if $K_1=0$,we have ${{\cal V}_H} = \{ \Psi \in {\bf{R}}|\Psi \in \{ 0,\;{K_0}\} \} {\;^1}$ Note '(x) $\varphi \left( x \right)$ lies in the first and third quadrants and hence $\varphi(x)/x\geq 0$. On the other hand,the Lipschitz condition implies that $|\varphi(x)/x|\leq \gamma_{\varphi}$. Then,we have $\varphi(x)/x\leq \gamma_{\varphi}$. Considering that $\varphi(x)$ satisfies the sector-bounded condition,the Corollary 1 can be easily obtained.}.$
Note that during the process of a controller design we usually select the infimum of $K_0$ for the purpose of reduction of conservatism. Corollary~1 implies that all decentralized vector functions $\varphi(x)$ which globally satisfies both Lipschitz and sector-bounded conditions can be represented as $\varphi(x)$ $=$ $\Theta x$ where $\Theta$ belongs to the same bounded convex set $\mathcal {H}$. In this sense,the reformulated Lipschitz condition has the same conservatism as the sector-bounded condition to describe the nonlinearity $\varphi(x)$. However,based on the reformulated Lipschitz condition,we obtain LMI-based conditions for the synthesis of the dynamic controller (3) with more variable matrices which might reduce the conservatism compared to the sector-bounded method[25]. Although the reformulated Lipschitz property in Lemma 1 is less conservative than the traditional one,the parameterization of $\varphi_{ij}$ could cause potential conservatism. It is well-known that dead-zone (or saturation) function defined above is globally Lipschitz. Hence, Lemma 1 can be used to tackle the dead-zone (or saturation) nonlinearity: $\psi(v_c)=\frac{\psi(v_c)}{v_c}v_c={\rm diag}\{\Theta_{ii}\} v_c$ with $0$ $\leq$ $\Theta_{ii}$ $\leq$ $1$. However,this may cause conservatism during the synthesis of an anti-windup compensator[1]. In fact,it is an earlier method to tackle saturation nonlinearity[10]. In this paper,the following modified sector condition is used to deal with actuator saturation.
B. Modified Sector Condition
Lemma 2[28]. Consider the dead-zone nonlinearity $\psi(v_c)$,with saturation level $v_0>0$ and $\psi(v_c) \in {\bf R}^m$ and define the following associated set:
| \begin{align} \mathcal{S}({v_c},v) = \{ {v_c} \in {{\bf R} ^m},v \in {{\bf R} ^m}\left| { - {v_0} \le {v_c} - v \le {v_0}} \right.\}, \end{align} | (10) |
| \begin{align} \psi(v_c)^{\rm{T}}T(\psi(v_c)-v)\leq 0, \end{align} | (11) |
Defining now the following system matrices:
| \begin{align} &\tilde A = \begin{pmatrix} {A + {B_u}{D_{cu}}{C_y}}&{{B_u}{C_c}}\\ {{B_{cu}}{C_y}}&{{A_c}} \end{pmatrix},\notag\\[1mm] &{{\tilde B}_u} = \begin{pmatrix} { - {B_u}}\\ 0 \end{pmatrix},\nonumber\\[1mm] &{{\tilde B}_\psi } = \begin{pmatrix} 0&{{B_u}}\\ {{I_m}}&0 \end{pmatrix},\notag\\[1mm] &{{\tilde B}_w} = \begin{pmatrix} {{B_w} + {B_u}{D_{cu}}{D_{yw}}}\\ {{B_{cu}}{D_{yw}}} \end{pmatrix},\nonumber\\[1mm] &{{\tilde B}_\varphi } =\begin{pmatrix} {{B_\varphi } + {B_u}{D_{cu}}{D_{y\varphi }}}\\ {{B_{cu}}{D_{y\varphi }}} \end{pmatrix},\notag\\[1mm] &E = \begin{pmatrix} {{E_1}}\\ {{E_2}} \end{pmatrix},\nonumber\\[1mm] &\hat I_2^{\rm{T}} = \begin{pmatrix}0 \quad I_{{n_c}}^{\rm{T}}\end{pmatrix},\notag\\[1mm] &{{\tilde C}_c} = \begin{pmatrix}{D_{cu}}{C_y}\quad {C_c}\end{pmatrix},\nonumber\\[1mm] &{{\tilde C}_z} = \begin{pmatrix}{C_z} + {D_{zu}}{D_{cu}}{C_y}\quad {D_{zu}}{C_c}\end{pmatrix},\nonumber\\[1mm] &{{\hat I}_\Theta } = \Theta \begin{pmatrix}{I_n} \quad 0\end{pmatrix},\notag\\[1mm] &{{\tilde D}_{cw}} = {D_{cu}}{D_{yw}},\nonumber\\[1mm] &{{\tilde D}_{z\varphi }} = {D_{z\varphi }} + {D_{zu}}{D_{cu}}{D_{y\varphi }},\notag\\[1mm] &\hat I = \begin{pmatrix}0\quad {I_m}\end{pmatrix},\nonumber\\[1mm] &{{\tilde D}_{zw}} = {D_{zw}} + {D_{zu}}{D_{cu}}{D_{yw}}, \end{align} | (12) |
| \begin{align} &\dot \xi = \hat A(\Theta )\xi + ({{\tilde B}_\psi }E + {{\tilde B}_u})\psi ({v_c}) + {{\tilde B}_w}w,\nonumber\\[1mm] &z = {{\hat C}_z}(\Theta )\xi + ({D_{zu}}\hat IE - {D_{zu}})\psi ({v_c}) + {{\tilde D}_{zw}}w,\notag\\[1mm] &{v_c} = {{\hat C}_c}(\Theta )\xi + {D_{cu}}{D_{yw}}w + \hat IE\psi ({v_c}),\label{eqq13} \end{align} | (13) |
| \begin{align} &\bar A = \tilde A + {{\tilde B}_\varphi }{{\hat I}_\Theta },\hat A = \bar A - {{\tilde B}_u}{D_{c\varphi }}{{\hat I}_\Theta } + {{\hat I}_2}{B_{c\varphi }}{{\hat I}_\Theta },\nonumber\\[1mm] &{{\bar C}_z} = {{\tilde C}_z} + {{\tilde D}_{z\varphi }}{{\hat I}_\Theta },{{\hat C}_z} = {{\bar C}_z} + {D_{zu}}{D_{c\varphi }}{{\hat I}_\Theta },\nonumber\\[1mm] &{{\bar C}_c} = {{\tilde C}_c} + {D_{cu}}{D_{y\varphi }}{{\hat I}_\Theta },{{\hat C}_c} = {{\bar C}_c} + {D_{c\varphi }}{{\hat I}_\Theta }. \end{align} | (14) |
In this paper,simultaneous anti-windup and nonlinear controller synthesis problems will be discussed to address the following problems [14, 25, 29] regarding the closed-loop system (13):
1) Estimate the region of attraction. In the absence of disturbances $w(t)$,we would like to determine an ellipsoid $\mathcal {E}(P)$ as large as possible such that the trajectories of the closed-loop system asymptotically converge to the origin with any initial point in it.
2) Determine the $\mathcal {L}_2$ gain. With a disturbance $w(t)$ satisfying (2),we would like to design an anti-windup-based dynamic controller (3) to ensure the trajectories of the closed-loop system remain bounded. Moreover,the $\mathcal {L}_2$-gain from the disturbance $w(t)$ to the performance output $z(t)$ should be minimized.
III. MAIN RESULTS
In this section,main result of this paper is shown. Particularly,we present LMI-based conditions for simultaneous synthesis of a nonlinear controller and a static anti-windup compensator for saturated Lipschitz system (1). It is shown that the conditions are in BMI forms. However,the synthesis conditions can be transformed into LMIs if we add some constraints on $B_{c\varphi}$ and $D_{c\varphi}$.
Define the following polyhedral set:
| \begin{align} {{\cal S}_1} = \{ \xi ||({\hat C_c}(\Theta ) - H(\Theta ))\xi {|_i} \le {v_{0i}},\; i=1,\ldots,m\}. \end{align} | (15) |
| \begin{align} \psi {({v_c})^{\rm{T}}}{T_1}(\psi ({v_c}) - H(\Theta )\xi - {D_{cu}}{D_{yw}}w - \hat IE\psi ({v_c})) \le 0, \end{align} | (16) |
$\textbf{Theorem 1.}$ Consider the nonlinear system (1). If there exist two positive-definite matrices $P_1,W_1 \in {\bf R} ^{n \times n}$,a diagonal positive-definite matrix $S_1 \in {{\bf R} ^{m \times m}}$,matrices $D_{cu} \in {\bf R}^{m \times q}$, $H_1(\Theta)\in {\bf R}^{m \times n}$,$\Sigma_1 \in {\bf R}^{n \times n}$,$\Sigma_2 \in {\bf R}^{n \times q}$,$\Sigma_3 \in {\bf R}^{n \times r}$,$\Sigma_4$ $\in$ ${\bf R}^{m \times r}$,$\Sigma_5 \in {\bf R}^{m \times n}$,$\Sigma_6(\Theta) \in {\bf R}^{n \times m}$,$\Sigma_7 \in {\bf R}^{n \times m}$,$M_2$ $\in$ ${\bf R}^{m \times m}$ and positive scalars $\gamma $ and $\lambda$ such that the following inequalities are satisfied for all $\Theta \in \mathcal {V}_\mathcal {H}$:
| \[\left( {\begin{array}{*{20}{c}} {{\Omega _1}}&{{\Omega _2}}&{{\Omega _6}}&{{\Omega _9}}&{{\Omega _3}}\\ \star &{{\Omega _4}}&{{\Sigma _7} + H_1^{\rm{T}}}&{{\Omega _{10}}}&{{\Omega _5}}\\ \star & \star &{ - 2{S_1} + He\{ {M_2}\} }&{{D_{cu}}{D_{yw}}}&{\Omega _7^{\rm{T}}}\\ \star & \star & \star &{ - I}&{\Omega _8^{\rm{T}}}\\ \star & \star & \star & \star &{ - \gamma I} \end{array}} \right) < 0,\] | (17) |
| \[\left( {\begin{array}{*{20}{c}} {{W_1}}& \star & \star \\ I&{{P_1}}& \star \\ {{\Omega _{11}}_i}&{{\Omega _{12}}_i}&{\lambda v_{0i}^2} \end{array}} \right) > 0,\] | (18) |
| \[\left( {\begin{array}{*{20}{c}} {{W_1}}& \star & \star \\ I&{{P_1}}& \star \\ {{\tau _k}{W_1}}&{{\tau _k}}&{\lambda \kappa _k^2} \end{array}} \right) > 0,\] | (19) |
| \begin{align} &{\Omega _1} = He\left\{ {A{W_1} + {B_u}{\Sigma _5} + {B_\varphi }\Theta {W_1} + {B_u}{\Sigma _4}\Theta {W_1}} \right\},\nonumber\\[1mm] &{\Omega _2} = A + {B_u}{D_{cu}}{C_y} + \Sigma _1^{\rm{T}} + {B_\varphi }\Theta + {B_u}{\Sigma _4}\Theta + {({\Sigma _3}\Theta {W_1}) ^{\rm{T}}},\notag\\[1mm] &{\Omega _3} = {({C_z}{W_1} + {D_{zu}}{\Sigma _5})^{\rm{T}}} + {W_1}{\Theta ^{\rm{T}}}{( {D_{z\varphi }} + {D_{zu}}{\Sigma _4}) ^{\rm{T}}},\nonumber\\[1mm] &{\Omega _4} = He\left\{ {{P_1}A + {\Sigma _2}{C_y} + {\Sigma _3}\Theta } \right\},\nonumber\\[1mm] &{\Omega _5} = {({C_z} + {D_{zu}}{D_{cu}}{C_y})^{\rm{T}}} + {\Theta ^{\rm{T}}}{( {D_{z\varphi }} + {D_{zu}}{\Sigma _4}) ^{\rm{T}}},\notag\\[1mm] &{\Omega _6} = {B_u}{M_2} - {B_u}{S_1} + {\Sigma _6},\notag\\[1mm] &{\Omega _7} = {D_{zu}}{M_2} - {D_{zu}}{S_1},\notag\\[1mm] &{\Omega _8} = {D_{zw}} + {D_{zu}}{D_{cu}}{D_{yw}},\notag\\[1mm] &{\Omega _9} = {B_w} + {B_u}{D_{cu}}{D_{yw}},\notag\\[1mm] &{\Omega _{10}} = {P_1}{B_w} + {\Sigma _2}{D_{yw}},\notag\\[1mm] &{\Omega _{11}} = {\Sigma _4}\Theta {W_1} + {\Sigma _5} - \Sigma _6^{\mathop{\rm T}\nolimits},\notag\\[1mm] &{\Omega _{12}} = {D_{cu}}{C_y} + {\Sigma _4}\Theta - {H_1}, \end{align} | (20) |
1) The trajectories of the closed-loop system are bounded for all vectors $w(t)$ satisfying (2); moreover,with null initial values,$\xi (t) \in \mathcal {E}(\lambda P)$ for all $t\geq0$, and the performance output $z$ satisfies $\left\| z \right\|_2^2 < \gamma \left\| w \right\|_2^2$.
2) When $w(t)=0$,the corresponding trajectories converge asymptotically to the origin for any initial states belonging to the set $\mathcal {E}(\lambda P)$.
Moreover,when variable matrices are obtained,the system matrices in the nonlinear controller (3) can be constructed by:
| \begin{align} &{B_{cu}} = P_2^{ - 1}({\Sigma _2} - {P_1}{B_u}{D_{cu}}),\nonumber\\[1mm] &{A_c} = P_2^{ - 1}({\Sigma _1} - {P_1}A{W_1} - {P_1}{B_u}{\Sigma _5}\nonumber\\[1mm] &\;\;\;\;\;\;\;\;- {P_2}{B_{cu}}{C_y}{W_1}){( W_2^{\rm{T}}) ^{ - 1}},\nonumber\\[1mm] &{D_{c\varphi }}={\Sigma _4} - {D_{cu}}{D_{y\varphi }},\nonumber\\[1mm] &{B_{c\varphi }}=P_2^{{\rm{ - }}1}({\Sigma _3} - {P_1}{B_\varphi } - {\Sigma _2}{D_{y\varphi }} - {P_1}{B_u}{D_{c\varphi }}),\notag\\[1mm] &{C_c} = ({\Sigma _5} - {D_{cu}}{C_y}{W_1}){( W_2^{\rm{T}}) ^{ - 1}},\nonumber\\[1mm] &{E_1} = P_2^{ - 1}({\Sigma _7} + {P_1}{B_u}{S_1} - {P_1}{B_u}{M_2}){S_1}^{ - 1},\nonumber\\[1mm] &{E_2} = {M_2}S_1^{ - 1}. \end{align} | (21) |
$\textbf{Proof.}$ Consider a quadratic Lyapunov function $V=\xi^{\rm{T}}P\xi$ with $P=P^{\rm{T}}>0$ and $W=P^{-1}$. Partitioning matrices $P$ and $W$ according to $\xi=[x^{\rm{T}}~x_c^{\rm{T}}]^{\rm{T}}$ such that[30]
| \begin{align*}P = \begin{pmatrix} {{P_1}}&{{P_2}}\\[1mm] {P_2^{\rm{T}}}& * \end{pmatrix},~,W = \begin{pmatrix} {{W_1}}&{{W_2}}\\[1mm] {W_2^{\rm{T}}}&* \end{pmatrix},~,\Pi =\begin{pmatrix} {{W_1}}&{{W_2}}\\[1mm] I_n&0 \end{pmatrix}.\end{align*} |
| \begin{align} \int\nolimits_0^t {{\cal J}(t){\rm d}t} =&,V(t) - V(0)\notag\\ &,+ \frac{1}{\gamma }\int\nolimits_0^t {{z^{\rm{T}}}z{\rm d}t} - \int\nolimits_0^t {{w^{\rm{T}}}w{\rm d}t} < 0,\label{eqq22} \end{align} | (22) |
Define new variables as follows:
| \begin{align} &{\Sigma _1} = {P_1}A{W_1} + {P_1}{B_u}{\Sigma _5} + {P_2}{B_{cu}}{C_y}{W_1} + {P_2}{A_c}W_2^{\rm{T}},\nonumber\\[1mm] &{\Sigma _2} = {P_1}{B_u}{D_{cu}} + {P_2}{B_{cu}},\nonumber\\[1mm] &{\Sigma _3} = {P_1}{B_\varphi } + {\Sigma _2}{D_{y\varphi }} + {P_1}{B_u}{D_{c\varphi }} + {P_2}{B_{c\varphi }},\nonumber\\[1mm] &{\Sigma _4} = {D_{cu}}{D_{y\varphi }} + {D_{c\varphi }},\notag\\[1mm] &{\Sigma _5} = {D_{cu}}{C_y}{W_1} + {C_c}W_2^{\rm{T}},\nonumber\\[1mm] &{\Sigma _6} = {W_1}{H_1}{(\Theta )^{\rm{T}}} + {W_2}{H_2}{(\Theta )^{\rm{T}}},\nonumber\\[1mm] &{\Sigma _7} = {P_2}{M_1} + {P_1}{B_u}{M_2} - {P_1}{B_u}{S_1}, \end{align} | (23) |
| \[\left( {\begin{array}{*{20}{c}} P& \star \\ {\left( {\begin{array}{*{20}{c}} {{\tau _k}}&0 \end{array}} \right)}&{\lambda \kappa _k^2} \end{array}} \right) > 0,\;\;k = 1,\ldots ,n,\] |
| \begin{align*}\begin{pmatrix} P&\star\\[1mm] {{{({{\hat C}_c}(\Theta ) - H(\Theta ))}_i}}&{\lambda v_{0i}^{\rm{T}}} \end{pmatrix} > 0,\ \ i = 1,\ldots ,m, \end{align*} |
| \begin{align} &{\cal J}(t) - 2\psi {({v_c})^{\rm{T}}}{T_1}(\psi ({v_c}) - H(\Theta )\xi - {D_{cu}}{D_{yw}}w \nonumber\\[1mm] &\qquad - \hat IE\psi ({v_c})) < 0.\label{eqq24} \end{align} | (24) |
| \begin{align} \begin{pmatrix} {He\{ P\hat A(\Theta )\} }&\Sigma_8&{P{{\tilde B}_w}}&{{{\hat C}_z}{{(\Theta )}^{\rm{T}}}}\\[1mm] \star&\Sigma_{9}&{{T_1}{D_{cu}}{D_{yw}}}&\Sigma_{10}^{\rm{T}}\\[1mm] \star&\star&{ - I}&{{{\tilde D}_{zw}}^{\rm{T}}}\\[1mm] \star&\star&\star&{ - \gamma I} \end{pmatrix} < 0,\label{eqq25} \end{align} | (25) |
Let's prove the second item. Considering $w(t)=0$,$\mathcal {J}(t)$ $<$ $0$ implies that $\dot V \le - 1/\gamma {z^{\mathop{\rm T}\nolimits} }z<0$,provided that ${\cal E}(\lambda P)$ $\subseteq$ ${{\cal B}_\varphi} \cap {{\cal S}_1 }$. Based on the above discussion, the validity of inequalities (18) and (19) assures the inclusion of $\mathcal {E}(\lambda P)$ in ${{\cal S}_1 }$ $\cap$ ${{\cal B}_\varphi}$. Hence,for all $t\geq0$ and $\xi (0) \in \mathcal {E}(\lambda P)$,$\dot V <0$,which concludes the proof.
$\square$
$\textbf{Remark~1.}$ Inequalities (18) and (19) imply that $I-P_1W_1>0$. Hence,there always exists nonsingular matrix $P_2$, $W_2$ such that $P_2W_2^{\rm{T}}=I-P_1W_1$. Note that matrix $W_2$ does not appear in inequality (17),(18),(19). One can assign any nonsingular value to matrix $W_2$ (e.g.,$W_2=I_n$),and then calculate matrix $P_2$ by equation $P_2=(I-P_1W_1)\{W_2^{\rm{T}}\}^{-1}$.
$\textbf{Remark~2.}$ The result of Theorem 1 can be applied to treat the case that the nonlinearity $\varphi(x)$ globally satisfies the Lipschitz condition (4). For this purpose,it suffices to eliminate the inequality (19).
$\textbf{Remark~3.}$ In matrices $P$,$W$,"$*$" are any matrices such that $PW=I_{2n}$ is verified.
$\textbf{Remark~4.}$ Due to the existence of nonlinear terms $\Sigma_3\Theta W_1$ and $\Sigma_4\Theta W_1$,the inequalities in Theorem 1 are in BMI forms. Hence,the ILMI optimization procedure[27] can be applied to obtain a suboptimal solution. Note since in each iterative step the synthesis conditions are affine in matrix $\Theta$ we only need to ensure the feasibility of the LMIs for each $\Theta \in \mathcal {V}_\mathcal {H}$. Consider now the case that $\Sigma_3=0$ and $\Sigma_4=0$ (or equivalently ${B_{c\varphi }}$ $=$ $ - P_2^{{\rm{ - }}1}({P_1}{B_\varphi } + {\Sigma _2}{D_{y\varphi }} + {P_1}{B_u}{D_{c\varphi }})$,$D_{c\varphi} = - {D_{cu}}{D_{y\varphi }}$. Particularly,if $D_{y\varphi}=0$,we have $D_{c\varphi}\equiv 0$). The synthesis conditions in Theorem 1 can be transformed into LMIs and well-developed convex optimization algorithm[32] can be implemented to obtain optimal solutions.
$\textbf{Remark~5.}$ Theorem 1 can also be utilized to synthesize the controller (3) with $B_{c\varphi}=0$ and $D_{c\varphi}=0$. In this case,according to remark 4,BMI conditions have to be solved (even if ${D_{y\varphi }} = 0$). It is pointed out that,under the assumption that ${D_{y\varphi }}$ $=$ $0$,it is possible to obtain LMI synthesis conditions by the methods proposed in [8] (omitted here). However,in this context,it is hard to place the closed-loop poles in a given conic sector (see also Remark~6).
$\textbf{Remark~6.}$ Utilizing the inequalities in Theorem 1 to design the dynamic controller (3) may cause ill-conditioned solutions. In this case,pole placement constraints can be incorporated in the optimization process to obtain a regional and suboptimal solution[33]. Considering the eigenvalues of $\tilde A$ given by $x_i+iy_i$,$i=1,\ldots,2n$,according to [33],if there exists a positive-definite matrix $W_0$ such that the following LMIs hold:
| \[\tilde A{W_0} + {W_0}{{\tilde A}^{\rm{T}}} + 2h{W_0} > 0,\] | (26) |
| \[\left( {\begin{array}{*{20}{c}} { - r{W_0}}&{\tilde A{W_0}}\\ {[1mm] \star }&{ - r{W_0}} \end{array}} \right) < 0,\] | (27) |
| \[\left( {\begin{array}{*{20}{c}} {{\Upsilon _1}}&{{\Upsilon _2}}\\ {[1mm] \star }&{{\Upsilon _1}} \end{array}} \right) < 0,\] | (28) |
| \begin{align*} {W_0} = W,\;\;\;\;\;\Gamma =\begin{pmatrix} {{I_n}}&0\\[1mm] {{P_1}}&{{P_2}} \end{pmatrix}. \end{align*} |
| \begin{align} \left( {\begin{array}{*{20}{c}} {He\{ A{W_1} + {B_u}{\Sigma _5} + h{W_1}\} }&\Upsilon_3+2h{I_n}\\[1mm] \star&\Upsilon_4+ 2h{P_1} \end{array}} \right) > 0, \end{align} | (29) |
| \[\left( {\begin{array}{*{20}{c}} { - r{W_1}}&{ - rI}&{A{W_1} + {B_u}{\Sigma _5}}&{A + {B_u}{D_{cu}}{C_y}}\\ {[1mm] \star }&{ - r{P_1}}&{{\Sigma _1}}&{{P_1}A + {\Sigma _2}{C_y}}\\ {[1mm] \star }& \star &{ - rW}&{rI}\\ {[1mm] \star }& \star & \star &{ - r{P_1}} \end{array}} \right) < 0,\] | (30) |
| \[\left( {\begin{array}{*{20}{c}} {\sin \theta {\Delta _1}}&{\cos \theta {\Delta _2}}\\ {[1mm] \star }&{\sin \theta {\Delta _1}} \end{array}} \right) < 0,\] | (31) |
| \[{\Delta _1} = \left( {\begin{array}{*{20}{c}} {He\{ A{W_1} + {B_u}{\Sigma _5}\} }&{{\Upsilon _3}}\\ {[1mm] \star }&{He\{ {\Upsilon _4}\} } \end{array}} \right),\] | (32) |
| \[\begin{array}{*{20}{l}} {{\Delta _2} = \left( {\begin{array}{*{20}{c}} {A{W_1} + {B_u}{\Sigma _5} - {{(A{W_1} + {B_u}{\Sigma _5})}^{\rm{T}}}}\\ {[1mm]{\Sigma _1} - {{(A + {B_u}{D_{cu}}{C_y})}^{\rm{T}}}} \end{array}} \right.}\\ {\left. {\quad \quad \qquad \qquad \begin{array}{*{20}{c}} {A + {B_u}{D_{cu}}{C_y} - \Sigma _1^{\rm{T}}}\\ {{P_1}A + {\Sigma _2}{C_y} - {{({P_1}A + {\Sigma _2}{C_y})}^{\rm{T}}}} \end{array}} \right).} \end{array}\] | (33) |
$\textbf{Remark 7.}$ In order to utilize Theorem 1 to estimate the ROA of the close-loop system,the synthesis conditions in Theorem 1 should be modified: set $\lambda=1$ (without loss of generality); delete the columns and rows related to performance output $z(t)$ and exogenous input $w(t)$. Since the matrix $W$ or $P$ cannot be entirely constructed,we aim at maximizing the region of attraction along the plant state directions (i.e.,${\mathcal {E}(P_1)}$) by solving the following convex optimization problem[29]:
| \begin{align} & {\min }\ \ {{\rm tr}(R)},\nonumber\\[1mm] & {\rm s.t.}\quad{R - {P_1} > 0},\notag\\[1mm] &\qquad\ (17)\mbox{-}(19)\ {\rm and}\ (29)\mbox{-}(31). \end{align} | (34) |
| \begin{align} &{{\dot x}_1} = {x_1} - {x_2} + 2sat({v_c}) + 2w(t),\nonumber\\[1mm] &{{\dot x}_2} = {x_1} - 3{x_2} + sat({v_c}) + \varphi (x) + w(t),\nonumber\\[1mm] &y = z = {x_1},\label{eqq53} \end{align} | (35) |
Firstly,we consider that the nonlinearity is given by $\varphi(x)$ $=$ $\frac{1.4 \times 1.8}{\pi}{\rm sin}(\frac{\pi}{1.8}x_1)$ which satisfies global Lipschitz condition (with Lipschitz constant $\gamma_{\varphi}=1.4$) and regional sector-bounded condition[25] (with $\Omega=1.4$ in the region $\mathcal {S}=\{x$ $\in$ ${\bf R}^n\|x_1|$ $\leq$ $1.8\}$). According to the definition of $\varphi_{ij}$ in Section III,we have $\varphi_{11}=\frac{2.52}{\pi}{\rm sin}(\frac{\pi}{1.8}x_1)/x_1$ which globally satisfies\footnote{For the reason that $\Omega=\overline{\gamma}_{\varphi_{11}}$, please refer to Corollary 1.} $-0.3041\leq\varphi_{11}\leq1.4$ (see Fig. 1). Hence,the matrix $\Theta$ belongs to the set for which the set of vertices is defined by ${{\cal V}_{\cal H}}$ $=$ $\{ {\Phi \in {{\bf R} ^{1 \times 2}}| {{\Phi} \in \{ (-0.3041~0),(1.4~0) \}}} \}$. Consider the disturbance rejection problem (i.e.,minimization of $\mathcal {L}_2$ gain $\sqrt{\gamma}$). Select $h=100$,$\theta={45^ \circ }$,$\lambda=1$. We obtain $\gamma$ $=$ $0.2600$ and the following controller matrices by Theorem 1:
| \[\begin{array}{l} {A_c} = \left( {\begin{array}{*{20}{c}} { - 89.5651}&{ - 55.2709}\\ {[1mm]14.9625}&{6.9974} \end{array}} \right),{B_{cu}} = \left( {\begin{array}{*{20}{c}} { - 0.4581}\\ {[1mm]0.0544} \end{array}} \right),\\ [1mm]{B_{c\varphi }} = \left( {\begin{array}{*{20}{c}} { - 0.4170}\\ {[1mm]0.1044} \end{array}} \right),{E_1} = \left( {\begin{array}{*{20}{c}} { - 3.2704}\\ {[1mm]0.5621} \end{array}} \right),\begin{array}{*{20}{c}} {{E_2} = 0.2546,}\\ {[1mm]} \end{array}\\ [1mm]{D_{c\varphi }} = 0,{C_c} = \left( {\begin{array}{*{20}{c}} {49.2638}&{270.4055} \end{array}} \right),{D_{cu}} = - 46.3999. \end{array}\] |
| \[w(t) = \left\{ {\begin{array}{*{20}{l}} {10,}&{{\rm{if}}0 < t \le 0.01}\\ {[1mm]0,}&{{\rm{if}}t > 0.01} \end{array}} \right..\] |
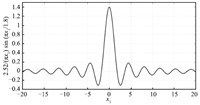 | Download: |
| Fig. 1 Function $\varphi_{11}(x)$. | |
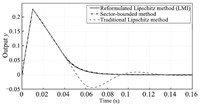 | Download: |
| Fig. 2 Time responses of the output by different control strategies. | |
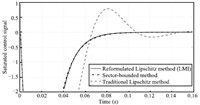 | Download: |
| Fig. 3 Time responses of the saturated control signals by different control strategies. | |
Consider now the stability analysis problem. An implicit objective in the synthesis of a stabilizing controller is the maximization of the ROA of the closed-loop system. Selecting $h$ $=$ $50$, $\theta={45^ \circ }$ and solving the convex optimization problem (34),the obtained results in five cases\footnote{Due to $D_{y\varphi}=0$,according to Remark 4,$\Sigma_3=0$ and $\Sigma_4=0$ imply that $B_{c\varphi}\neq0$ and $D_{c\varphi}=0$. Solving a set of LMI constraints,we obtain the suboptimal value ${\rm tr}(P_1)=0.0615$. Then,we initialize the ILMI algorithm by the obtained matrix $W_1$ to design two kinds of anti-windup controller (3): $B_{c\varphi}$ $=$ $0$,$D_{c\varphi}=0$; $B_{c\varphi}\neq0$,$D_{c\varphi}\neq0$.} are shown in Table~I and Fig. 4. Compared with the traditional Lipschitz method[26] and sector-bounded method[25],the method presented in Theorem 1 has led to the largest estimated ROA. Since the region $\mathcal {S}$ has restricted the size of $\mathcal {E}(P_1)$,the sector-bounded method leads to large conservatism. Hence,during the synthesis of a dynamic controller,regional inequality condition description should be avoided.
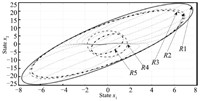 | Download: |
| Fig. 4 Comparison of estimated region of attractions ($\varphi(x)=\frac{2.52}{\pi}$ $\times$ ${\rm sin}(\frac{\pi}{1.8}x_1)$). In particular,$R$1 (by Theorem 1 with $B_{c\varphi}\neq0$,$D_{c\varphi}$ $\neq$ $0$); $R$2 (by Theorem 1 with $B_{c\varphi}\neq0$,$D_{c\varphi}=0$); $R$3 (by Theorem 1 with $B_{c\varphi}=0$,$D_{c\varphi}=0$); $R$4 (sector-bounded method[25]); $R$5 (traditional Lipschitz method[26]). | |
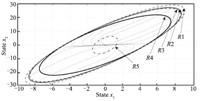
Consider the case that the nonlinearity is given by $\varphi(x)={\rm tanh}(1.5x_1)$ which globally satisfies Lipschitz condition (with Lipschitz constant $\gamma_{\varphi}=1.5$). It can be verified that the matrix $\Theta$ belongs to the set for which the set of vertices is defined by ${{\cal V}_{\cal H}} = \{ {\Phi \in {{\bf R} ^{1 \times 2}}| {{\Phi} \in \{ (0~0),(1.5~0) \}}} \}$. Selecting $h$ $=$ $100$,$\theta={45^ \circ }$,the estimated ROA in five cases are shown in Fig. 5. From the perspective of traditional Lipschitz condition,the Lipschitz constant only increases by 0.1 and hence size of the estimated ROA varies not too much (even though the parameter $h$ is increased) which inevitably causes large conservatism by the method in [26] (${\rm tr}(P_1)= 0.6546$). On the other hand,$\varphi(x)$ globally satisfies the sector-bounded condition[25] (with $\Omega=1.5$). Hence,no constraints on the size of the ROA need to be considered. The obtained estimated ROA increases greatly (${\rm tr}(P_1)= 0.0512$). In spite of this,the largest size of the estimated ROA has been obtained by the method proposed in this paper (${\rm tr}(P_1)=0.0491$). In Table II,the performances\footnote{In which the minimization of $\lambda$ implies the largest disturbance energy that the closed-loop system can tolerate[14].} under different strategies have been compared. One can easily find,similar as the estimation of ROA,Theorem 1 has led to the best closed-loop performances.
 | Download: |
| Fig. 5 Comparison of estimated region of attractions ($\varphi(x)=\tanh(1.5x_1)$). In particular,$R$1 (by Theorem 1 with $B_{c\varphi}\neq0$,$D_{c\varphi}$ $\neq$ $0$); $R$2 (by Theorem 1 with $B_{c\varphi}\neq0$,$D_{c\varphi}=0$); $R$3 (by Theorem 1 with $B_{c\varphi}=0$,$D_{c\varphi}=0$); $R$4 (sector-bounded method[25]); $R$5 (traditional Lipschitz method[26]). | |
| Table I COMPARISON OF THE ESTIMATED ROA BY DIFFERENT METHODS |
V. CONCLUSION
In this paper,anti-windup-based dynamic controller design techniques have been presented for Lipschitz systems subject to actuator saturation. The methods mainly rely on the so-called reformulated Lipschitz property by which the saturated nonlinear systems can be transformed into LPV systems. With the modified sector-bounded condition tackling the saturation nonlinearity,BMI conditions for the synthesis of an anti-windup-based nonlinear controller are proposed which can be solved at the vertices of a bounded convex set by ILMI optimization procedures (for a certain kind of nonlinear controller,only LMI conditions need to be solved). A numerical example has illustrated the effectiveness of the proposed methods.
| Table II COMPARISON OF PERFORMANCES BY DIFFERENT METHODS |
| [1] | Tarbouriech S, Turner M C. Anti-windup design: an overview of some recent advances and open problems. IET Control Theory and Applications, 2009, 3(1): 1-19 |
| [2] | Teel A R, Kapoor N. The L2 anti-windup problem: its definition and solution. In: Proceedings of the 1997 European Control Conference. Brussels, Belgium: IEEE, 1997. 1897-1902 |
| [3] | Grimm G, Hatfield J, Postlethwaite I, Teel A R, Turner M C, Zaccarian L. Antiwindup for stable linear systems with input saturation: an LMIbased synthesis. IEEE Transactions on Automatic Control, 2003, 48(9): 1509-1525 |
| [4] | Gomes da Silva Jr J M, Tarbouriech S. Antiwindup design with guaranteed regions of stability: an LMI-based approach. IEEE Transactions on Automatic Control, 2005, 50(1): 106-111 |
| [5] | Wu F, Soto M. Extended anti-windup control schemes for LTI and LFT systems with actuator saturations. International Journal of Robust and Nonlinear Control, 2004, 14(15): 1255-1281 |
| [6] | Turner M C, Herrmann G, Postlethwaite I. Incorporating robustness requirements into antiwindup design. IEEE Transactions on Automatic Control, 2007, 52(10): 1842-1855 |
| [7] | Hu T S, Teel A R, Zaccarian L. Stability and performance for saturated systems via quadratic and nonquadratic Lyapunov functions. IEEE Transactions on Automatic Control, 2006, 51(11): 1770-1786 |
| [8] | Dai D, Hu T S, Teel A R, Zaccarian L. Output feedback design for saturated linear plants using deadzone loops. Automatica, 2009, 45(12): 2917-2924 |
| [9] | Mulder E F, Tiwari P Y, Kothare M V. Simultaneous linear and antiwindup controller synthesis using multiobjective convex optimization. Automatica, 2009, 45(3): 805-811 |
| [10] | Wu F, Grigoriadis K M, Packard A. Anti-windup controller design using linear parameter-varying control methods. International Journal of Control, 2000, 73(12): 1104-1114 |
| [11] | Prempain E, Turner M C, Postlethwaite I. Coprime factor based antiwindup synthesis for parameter-dependent systems. Systems and Control Letters, 2009, 58(12): 810-817 |
| [12] | Kahveci N E, Ioanou P A, Mirmirani M D. A robust adaptive control design for gliders subject to actuator saturation nonlinearities. In: Proceedings of the 2007 American Control Conference. New York: IEEE, 2007. 492-497 |
| [13] | Gomes da Silva Jr J M, Oliveira M Z, Coutinho D, Tarbouriech S. Static anti-windup design for a class of nonlinear systems. International Journal of Robust and Nonlinear Control, 2014, 24(5): 793-810 |
| [14] | Wang N Z, Pei H L, Wang J, Zhang Q. Anti-windup design for rational systems by linear-fractional representation. IET Control Theory and Applications, 2014, 8(5): 355-366 |
| [15] | Teel A R, Kapoor N. Uniting local and global controllers. In: Proceedings of the 4th European Control Conference. Brussels, Belgium, 1997. |
| [16] | Morabito F, Teel A R, Zaccarian L. Nonlinear antiwindup applied to Euler-Lagrange systems. IEEE Transactions on Robotics and Automation, 2004, 20(3): 526-537 |
| [17] | Rehan M, Hong K S. Decoupled-architecture-based nonlinear antiwindup design for a class of nonlinear systems. Nonlinear Dynamics, 2013, 73(3): 1955-1967 |
| [18] | Herrmann G, Menon P P, Turner M C, Bates D G, Postlethwaite I. Anti-windup synthesis for nonlinear dynamic inversion control schemes. International Journal of Robust and Nonlinear Control, 2010, 20(13): 1465-1482 |
| [19] | Zames G, Falb P L. Stability conditions for systems with monotone and slope restricted nonlinearities. SIAM Journal on Control, 1968, 6(1): 89 -108 |
| [20] | Khalil H K. Nonlinear Systems (2nd edition). U. K.: Prentice Hall, 1996. |
| [21] | Gao J F, Su H Y, Ji X F, Chu J. Stability analysis for a class of neutral systems with mixed delays and sector-bounded nonlinearity. Nonlinear Analysis: Real World Applications, 2008, 9(5): 2350-2360 |
| [22] | Phanomchoeng G, Rajamani R, Piyabongkarn D. Nonlinear observer for bounded Jacobian systems, with applications to automotive slip angle estimation. IEEE Transactions on Automatic Control, 2011, 56(5): 1163 -1170 |
| [23] | Turner M C, Kerr L M. L2 gain bounds for systems with sector bounded and slope-restricted nonlinearities. International Journal of Robust and Nonlinear Control, 2012, 22(13): 1505-1521 |
| [24] | Zemouche A, Boutayeb M. On LMI conditions to design observers for Lipschitz nonlinear systems. Automatica, 2013, 49(2): 585-591 |
| [25] | Gomes da Silva Jr J M, Castelan E B, Corso J, Eckhard D. Dynamic output feedback stabilization for systems with sector-bounded nonlinearities and saturating actuators. Journal of the Franklin Institute, 2013, 350(3): 464-484 |
| [26] | Rehan M, Khan A Q, Abid M, Iqbal N, Hussain B. Anti-windupbased dynamic controller synthesis for nonlinear systems under input saturation. Applied Mathematics and Computation, 2013, 220: 382-393 |
| [27] | Peaucelle D, Arzelier D. An efficient numerical solution for H2 static output feedback synthesis. In: Proceedings of the 2001 European Control Conference. Porto Portugal: IEEE, 2001. 3800-3805 |
| [28] | Castelan E B, Tarbouriech S, Queinnec I. Stability and stabilization of a class of nonlinear systems with saturating actuators. In: Proceedings of the 16th IFAC World Congress. Check Republic: IFAC, 2005. 776-782 |
| [29] | Bender F A, Gomes da Silva Jr J M, Tarbouriech S. Convex framework for the design of dynamic anti-windup for state-delayed systems. IET Control Theory and Applications, 2011, 5(12): 1388-1396 |
| [30] | Scherer G, Gahinet P, Chilali M. Multiobjective output-feedback control via LMI optimization. IEEE Transactions on Automatic Control, 1997, 42(7): 896-911 |
| [31] | Boyd S, El Ghaoui L, Feron E, Balakrishnan V. Linear Matrix Inequalities in System and Control Theory. Philadelphia, PA: SIAM, 1994. |
| [32] | Chilali M, Gahinet P. H∞ design with pole placement constraints: an LMI approach. IEEE Transactions on Automatic Control, 1996, 41(3): 358-367 |
 2015, Vol.2
2015, Vol.2 


