Ⅰ. INTRODUCTION

Over the past few years,wireless sensor network (WSN) has been applied widely in many fields,such as intelligent traffic,industrial and meteorological monitoring,and so on. WSN is usually composed of large amount of sensors that are randomly distributed in a certain region. WSN can perform collecting, processing and transmitting for large amount of data in one hop or multi-hop self-organization manner. Typically,sensor nodes are empowered by some low capacity batteries. Because of the special work environment,the energy resources of sensors are usually irreplaceable^[1]. Under such constraint condition,energy saving and lifetime prolonging become the hot topics in the researches of WSNs. The unbalance of energy consumption is a common problem in WSNs. There are some nodes that will relay data passively too much for others,and they become bottleneck nodes in the network. For the lack of information of the whole network,it may result in the death of some nodes earlier and the deterioration of network performance. So how to allocate the energy of nodes,adjust the transmitting rate and balance the energy consumption become an important issue^{[2, 3]}. References ^{[4, 5]} focused on the method of cross-layer design to achieve power control scheme and save energy. However,the extra overhead caused by frequently scheduling among different protocol layers cannot be avoided. That results in the poor performance in the aspect of information exchange. In order to get tradeoff between topology coverage and fault tolerance,Zhao et al,proposed a distributed adaptive power control scheme^[6], which could guarantee the connectivity of networks and prolong the lifetime. The problem of source extraction in bandwidth-constrained WSN was considered in ^[7],and three kinds of sensor network topologies were considered in order to show the impact of topology on the performance and energy efficiency.

From network performance respective,energy saving design of routing algorithm provides a promising approach for maximizing the lifetime of WSN. Generally,there are two types of routing protocol algorithms,flat routing and hierarchical routing^[8]. In cluster routing algorithms,the criterion of cluster selection adopted in existing research is usually based on a certain of rules,such as residual energy,coverage, probability of outage,and so on. The flexible and adaptive multi-hop network can be formed with the relaying of clusters, which is favorable for stochastic topology^[9].

Among clustering algorithms,low energy adaptive clustering hierarchy (LEACH) is one of the most recognized classical clustering algorithms in WSNs^[10]. LEACH selects cluster heads dynamically and frequently by a round mechanism,and allows different nodes to become cluster heads at each round. Some lately improved algorithms based on LEACH pay more attention to how to save energy and/or guarantee fairness,such as power efficient gathering in sensor information systems (PEGASIS),hybrid,energy-efficient,distributed (HEED),energy-efficient cluster formation (EECF). In routing protocol design,it is considered how to balance the energy consumption among nodes during the formation of cluster,and neglect the consumption during the data transmission. For the difference of roles,cluster head is in charge of data fusion,computation, storage,delivery,and consumes more energy^{[11, 12]}. In homogeneous network,cluster head and member nodes have the same features and energy constraints. Once the cluster head exhausts energy,the member nodes will loss the relay,and network reconfiguration and routing re-setup are needed. Frequent change of routing and topology will increase the network overhead and decrease the network performance^{[13, 14]}. Besides,some other network performances such as coverage,real-time and lifetime,are involved when the cluster routing is considered. In ^[15],the maximization of the coverage time for a clustered wireless sensor network by optimal balancing power consumption among cluster heads was considered, and stochastic as well as deterministic network models were investigated,respectively. In ^[16],a distributed energy-efficient clustering with improved coverage algorithm was proposed,which could cluster the sensor network with the least number of cluster heads to cover the whole network and assign a unique ID to each node only based on local information.

In this paper,regarding the special role of cluster head,it is proposed that performance of cluster head is protected first by reducing the interference from member nodes. Involving the effect and relation of power and rate,a novel joint optimization model is presented with the protection for cluster head. Based on the optimization model proposed in this paper,the cost function is designed and the dual decomposition method is adopted to get distributed optimal iterative algorithm. The efficiency of cluster head is improved and the extra cost,caused by the death of cluster head,is reduced. The network lifetime is prolonged effectively. By the mean of choosing two appropriate sub-utility functions,the distributed iterative algorithm is achieved.

The rest of the paper is organized as follows. In Section II,the network model and system formulation are given. The optimization strategy is proposed and the convergence of the algorithm is proven in Section III. Simulation results are given in Section IV to validate the effectiveness of the proposed algorithm. Finally, conclusions are drawn in Section V.

Ⅱ. NETWORK MODEL AND PROBLEM FORMULATION

Fig. 1 shows a schematic of the networks. The stationary network topology is considered. It contains $M$ sensor nodes and $N$ clusters randomly distributed in the sensing region. Let ${{\text{N}}_{\text{i}}}$ be the number of member nodes in cluster $i$. There are $L$ links, and the signal to interference plus noise ratio (SINR) in link $l$ is $\gamma_{l}$.

For the clustering routing,there usually are three phases,the phase of cluster set-up,stable operation and cluster update. Cluster head can be selected or migrated according to some routing rule or algorithm and it is neglected here. We focus on the period of stable transmission in each round. The cluster head,denoted as $CH_{n}$,can either communicates with base station (BS) directly or transmit data in multi-hop to a destination,depending on the routing algorithm. In a cluster,the cluster head takes the charge of relaying data from other member node. The energy consumption of cluster head will be more than other nodes. Once the cluster head exhausts energy,the whole cluster will not work. The topology will change with the join-in or quit of some nodes. Moreover,the interference among different clusters cannot be avoided,and this kind of interference will cause low communication quality,even failure of communication. So cluster heads play an important role in the WSNs. It is necessary to keep the topology stable by the mean of protecting cluster heads. For cluster $n$,the protection for cluster head $CH_{n}$ is formulated as threshold constraint.

$\begin{align} \sum\limits_{i = 1}^{{N_n}} {{p_i}{g_i}} < {Q_n}, \end{align}$

(1)

where \({g_i}\) is channel gain,\({p_i}\) is transmission power of node \({s_i}\),\({Q_n}\) is the demand of protection.

Denote $r_{i}$ as the transmission rate of node $i$,which is larger than the minimum rate,i.e.,$r_{i}>r_{\min}$. There exists a constraint of transmitting power and it is denoted as $p_{i}< p_{\max}$. According to Shannon principle of wireless communication,the channel capacity $c_{l}$ is as follows.

$\begin{align} c_l\left( p \right) = W{\log _2}\left( {1 + \frac{{p\zeta}}{{{d^a}}}} \right), \end{align}$

(2)

where \(W\) is bandwidth,\(p\) is average power,\(d\) is the distance and \(\zeta\) is a constant related to modulation,\(a \) is attenuation factor of channel and its typical value is 2~5. Denote \({\mathop{\rm s}\nolimits} \left( l \right)\) as the user set on link \(l\),\({c_l}\) as the capacity limitation. In fact,the actual rate is lower than \({c_l}\),so we model the constraint that link $l$ must satisfy the link capacity constrain as (3)

$\begin{align} \sum\limits_{j \in {\rm{s}}\left( l \right)} {{r_j} < \beta {c_l}}, \end{align}$

(3)

where $\beta $ is the efficiency factor,\(0 < \beta < 1\). The factor $\beta$ introduced here is to leave some leeway against channel uncertainty.

Next,we analyze the cost function of optimal problem. The objective is to get higher throughput with lower transmitting power. The optimization cost function is designed as the sum of each node's utility.

$\begin{align} U\left( {{\pmb r},{\pmb p}} \right) = \sum\limits_{i = 1}^M {G\left( {{r_i},{p_i}} \right)}. \end{align}$

(4)

Here \(G\left( {{r_i},{p_i}} \right)\) is an increasing function of \({r_i}\),and decreasing function of \({p_i}\). It means that the utility of network is to get more data exchange with less power consumption. Based on above description,we formulate the problem as a network utility maximum problem.

$\begin{align} &\max ~\sum\limits_{i = 1}^M {G\left( {{r_i},{p_i}} \right)},\notag\\ &\,{{\rm{s}}{\rm{.t}}{\rm{.}}}\quad {\sum\limits_{j \in {{s}}\left( l \right)} {{r_j}} < \beta {c_l}\left( p \right)},\ \quad& {l = 1,\ldots,L},\notag\\ &\qquad\ \ \,{\sum\limits_{i = 1}^{{N_n}} {{p_i}{g_i}} < {Q_n}},\ \quad& n = 1,\ldots,N,\notag\\ &\qquad\ \ \,{{r_i} > {r_{\min }}}, \ \quad& {i = 1,\ldots,M},\notag\\ &\qquad\ \ \,{{p_i} < {p_{\max }}},\ \quad& {i = 1,\ldots,M}. \end{align}$

Remark 1. The four constraints are interpreted as follows. The first one is the rate constraint; the second is the protection constraint for cluster head; the third and forth are variable constraint of rate and power,respectively.

To guarantee solvability of the optimal problem,the cost function $G(r,p)$ is chosen as a second derivable function of $r,p$,and it is a concave function of variables. Here we select the cost function as follows

$\begin{align} G\left( {{r_i},{p_i}} \right) = \alpha f_1\left( {{r_i}} \right) - \left( {1 - \alpha } \right)f_2\left( {{p_i}} \right), \end{align}$

(6)

where \(f_1\left( {{r_i}} \right)\) is a concave function of \({r_i}\),which can be regarded as the throughput benefit; \(f_2\left( {{p_i}} \right)\) is a convex function of \({p_i}\), which can be regarded as the payment of power consumption. \(\alpha \) is a weighted factor,which can reflect the emphasis on rate utility or power utility. So $G\left( {{r_i},{p_i}} \right)$ is the net income of node $i$. Here we use the sum of the net utility of all nodes as a measure of system performance. The objective of the optimal problem is to maximize the whole utility of the network.

Ⅲ. DESIGN OF JOINT OPTIMIZATION STRATEGY

The joint optimization problem is formulated as a nonlinear optimization problem. In problem (6),the goal is to maximize the sum of network utility. To fit the feature of distributed operation in large scale sensor networks,dual decomposition method is used. The Lagrangian dual function of problem (5) can be converted into

$\begin{align} & L\left( {{{\pmb r},{\pmb p},\lambda,\mu }} \right) = \sum\limits_{i = 1}^M {\left[{\alpha f_{1}\left( {{r_i}} \right) - \left( {1 - \alpha } \right)f_{2}\left( {{p_i}} \right)} \right]}\,\notag\\ &\quad -\sum\limits_{l = 1}^L {{\lambda _l}\left( {\sum\limits_{j \in {{s}} \left( l \right)} {{r_i}} - \beta {c_l}} \right)} - \sum\limits_{n = 1}^N {\mu _n}\left( {\sum\limits_{j = 1}^{{N_n}} {{p_j}{g_j}} - {Q_n}} \right), \end{align}$

(7)

where \({\pmb{r}} = [{{r_1},{r_2},\ldots,{r_n}}]\) is the vector of transmitting rate,${{\pmb p}}$ $=$ $[{{p_1},{p_2},\ldots, {p_n}}]$ is the vector of user power,${{\lambda }}=[{\lambda _1}, {\lambda _2}$,$\ldots$,${\lambda _n}]$ and \({\bf{\mu }} = [ {{\mu _1},{\mu _2},\ldots,{\mu _n}}]\) are vectors of Lagrangian multipliers,respectively. From above expression,the dual problem is given by

$\begin{align} \mathop {\min }\limits_{\lambda,\mu } \varphi \left( {\lambda ,\mu } \right), \end{align}$

(8)

where \(\varphi \left( {\lambda ,\mu } \right) = \mathop {\max }\nolimits_{{\pmb r},{\pmb p}} L\left( {{\pmb r},{\pmb p}} \right)\). In the dual formulation,Lagrange multipliers $\lambda, \mu$ can be interpreted as cost of constraint. One beneficial observation is that each node can compute its rate and power individually. For given multipliers $\lambda$ and $\mu$,the optimal power and rate can be obtained by solving the dual problem. To separate the variables,rewriting $L\left( {{\pmb r},{\pmb p}} \right)$,one has

$\begin{align} L\left( {{{\pmb r},{\pmb p}}} \right) =&\ \left[{\sum\limits_{i = 1}^M {\alpha f_{1}\left( {{r_i}} \right) - } \sum\limits_{l = 1}^L {{\lambda _l}\sum\limits_{j \in {\rm{s}}\left( l \right)} {{r_i}} } } \right] \notag\\ &\ -\left[{\sum\limits_{i = 1}^M {\left( {1 - \alpha } \right)f_{2}\left( {{p_i}} \right)} {\rm{ - }}\beta \sum\limits_{l = 1}^L {{\lambda _l}{c_l}}}\right.\notag\\ &\ -\left.{{\rm{ }}\sum\limits_{n = 1}^N {{\mu _n}\sum\limits_{j = 1}^{{N_n}} {{p_j}{g_j}} } } \right]{\rm{ + }}\sum\limits_{n = 1}^N {{\mu _n}{Q_n}}. \end{align}$

(9)

Thus $L({\pmb r},{\pmb p})$ can be divided into three parts. The first part can be converted to optimal rate sub-problem,the second part can be converted to optimal power sub-problem,and the last one is independent of ${\pmb r},{\pmb p}$. For given $\lambda$ and $\mu$,the third part is constant.

Sub-problem 1.

$\begin{align} &\max\ {L_1}\left( {{\pmb r}} \right) = \left[{\sum\limits_{i = 1}^M {\alpha f_{1}\left( {{r_i}} \right) - } \sum\limits_{l = 1}^L {{\lambda _l}\sum\limits_{j \in {\rm{s}}\left( l \right)} {{r_i}} } } \right],\notag\\[2mm] &\,{\rm{s}}{\rm{.t}}{\rm{. }}\quad {r_i} > {r_{\min }},\qquad\qquad\qquad\quad\ i = 1,\ldots,M. \end{align}$

(10)

Let \(\frac{{\partial {L_1}\left( {\bf{r}} \right)}}{{\partial {r_i}}} = 0\),one can get the optimal solution of rate \(r_i^*\) by solving (11)

$\begin{align} \alpha f'_{1}\left( {{r_i}} \right) = \sum\limits_{l = 1}^L {{\lambda _l}}. \end{align}$

(11)

Sub-problem 2.

$\begin{align} &\max\ {L_2}\left( {{\pmb p}} \right) = \sum\limits_{i = 1}^M {\left( {1 - \alpha } \right)f_{2}\left( {{p_i}} \right)} {\rm{ - }}\beta \sum\limits_{l = 1}^L {{\lambda _l}{c_l}}\notag\\[2mm] &~~~~~~~~~~~~~~~~~{\rm{ }}-\sum\limits_{n = 1}^N {{\mu _n}\sum\limits_{j = 1}^{{N_n}} {{p_j}{g_j}}},\notag\\[2mm] &\,{\rm{s}}{\rm{.t}}\quad {\rm{ }}{p_i} < {p_{\max }},{\rm{ }}\qquad i = 1,\ldots,M. \end{align}$

(12)

Similarly,let \(\frac{{\partial {L_2}\left( {{\pmb p}} \right)}}{{\partial {p_i}}} = 0\) and solve (13),one can get the optimal power \(p_i^*\).

$\begin{align} \left( {1 - \alpha } \right)f'_{2}\left( {{p_i}} \right){\rm{ - }}\beta \sum\limits_{l = 1}^L {{\lambda _l}{c_l}'} {\rm{ - }}\sum\limits_{n = 1}^N {{\mu _n}{g_i}} = 0. \end{align}$

(13)

Obviously,the above two sub-problems are independent of variable $\lambda,~\mu$. Once the optimal $\lambda,~\mu$ are gained,it is easy to get the optimal solution. Next,we analyze the optimal multipliers $\lambda^{\ast},~\mu^{\ast}$ based on sub-gradient method. At time $t+1$,the multipliers are updated according to sub-gradient direction,and the rules are given as follows.

$\begin{align} &\lambda _l\left( {t + 1} \right) = {\left[{{\lambda _l}\left( t \right) - \delta \left( t \right)\frac{{\partial L\left( {{\bf{\lambda ,\mu }}} \right)}}{{\partial {\lambda _l}}}} \right]^ + },\end{align}$

(14)

$\begin{align} &{\mu _n}\left( {t + 1} \right) = {\left[{{\mu _n}\left( t \right) - \delta \left( t \right)\frac{{\partial L\left( {{\bf{\lambda ,\mu }}} \right)}}{{\partial {\mu _n}}}} \right]^ + }, \end{align}$

(15)

where $[\cdot]^+$ means that if the expression in the bracket is less than 0,the value is 0. $\delta(n)$ is an iterative step. The step has a major effect on convergence rate. Next,we prove that the multiplier can converge to the unique optimal point.

Without loss of generality,multiplier \(\lambda \) is taken as an example to analyze the convergence.

Definition 1. For an arbitrarily given \(\varepsilon > 0\),if there exists a bounded step series \(0 < \delta \left( t \right) < \bar \delta \),such that

$\begin{align} \lim\limits_{t \to \infty } \sup \left( {\frac{1}{t}\sum\limits_{\tau = 1}^t {\psi \left( {\lambda \left( \tau \right),\mu } \right)} - \psi \left( {{\lambda ^*},\mu } \right)} \right) \le \varepsilon. \end{align}$

(16)

Then the iterative algorithm can converge into the \(\varepsilon \) neighborhood of \({\lambda ^*}\),where \({\lambda ^*}\) is the optimal value of dual variable in dual system.

Theorem 1. Constructing the cost function as formula (6), where \(f( {{r_i}} ) = \log ( {\frac{{{r_i}}}{{{r_{\min }}}}} )\), \(g( {{p_i}} ) = {( {\frac{{{p_i}}}{{{p_{\max }}}}} )^2}\),the algorithm can approach to the optimal solution with arbitrary given precision.

Proof. It is supposed that sub-gradient of $L({{\pmb r}, {\pmb p}})$ is norm-bounded,i.e.,the norm of \(\frac{{\partial L( {{\bf{\lambda,\mu }}} )}}{{\partial {\lambda _l}}}\) has an upper bound \(\bar R\),then

$\begin{align} \left\| {\beta {c_l} - \sum\limits_{j \in {\rm{s}}\left( l \right)} {{r_j}} } \right\|_2 \leq \bar R. \end{align}$

(17)

According to the physical property of parameters,it is clear that the above condition is satisfied. From (14),one has

$\begin{align} &\left\| {\lambda \left( {t + 1} \right) - {\lambda ^*}} \right\|_2^2 \leq \left\| {\lambda \left( t \right) - \bar \delta \left( {\beta {c_l} - \sum\limits_{j \in {\rm{s}}\left( l \right)} {{r_j}} } \right) - {\lambda ^*}} \right\|_2^2 \notag\\ & \qquad \leq\left\| {\lambda \left( t \right) - {\lambda ^*}} \right\|_2^2 - 2\bar \delta \left( {\psi \left( {\lambda \left( t \right),\mu } \right) - \psi \left( {{\lambda ^*},\mu } \right)} \right)\notag\\ & \qquad +{{\bar \delta }^2}\left\| {\beta {c_l} - \sum\limits_{j \in {\rm{s}}\left( l \right)} {{r_j}} } \right\|_2^2\leq\left\| {\lambda \left( 1 \right) - {\lambda ^*}} \right\|_2^2 \notag\\ & \qquad - 2\bar \delta \sum\limits_{\tau = 1}^t {\left( {\psi \left( {\lambda \left( \tau \right),\mu } \right) - \psi \left( {{\lambda ^*},\mu } \right)} \right)} \notag\\ & \qquad +{{\bar \delta }^2}\sum\limits_{\tau = 1}^t {\left\| {\beta {c_l} - \sum\limits_{j \in {\rm{s}}\left( l \right)} {{r_j}} } \right\|_2^2}. \end{align}$

(18)

It is obvious that the left side of inequality is nonnegative,one has

$\begin{align} &2\bar \delta \sum\limits_{\tau = 1}^t {\left( {\psi \left( {\lambda \left( \tau \right),\mu } \right) - \psi \left( {{\lambda ^*},\mu } \right)} \right)} \notag\\ &\qquad \leq\left\| {\lambda \left( 1 \right) - {\lambda ^*}} \right\|_2^2 + {{\bar \delta }^2} \sum\limits_{\tau = 1}^t {\left\| {\beta {c_l} - \sum\limits_{j \in {\rm{s}}\left( l \right)} {{r_j}} } \right\|_2^2} \notag\\ &\qquad \leq\left\| {\lambda \left( 1 \right) - {\lambda ^*}} \right\|_2^2 + t{{\bar \delta }^2}{{\bar R}^2}. \end{align}$

(19)

Divided by $2t\bar \delta$ on both sides of (19),one can get

$\begin{align} \dfrac{1}{t}\sum\limits_{\tau = 1}^t {\left( {\psi \left( {\lambda \left( \tau \right),\mu } \right) - \psi \left( {{\lambda ^*},\mu } \right)} \right)} \leq \dfrac{{\left\| {\lambda \left( 1 \right) - {\lambda ^*}} \right\|_2^2 + t{{\bar \delta }^2}{{\bar R}^2}}}{{2\bar \delta t}}. \end{align}$

(20)

The limit of (20) can be expressed as%\vskip0.1mm\noindent

$\begin{align} \lim\limits_{t \to \infty } \sup \left( {\frac{1}{t}\sum\limits_{\tau = 1}^t {\psi \left( {\lambda \left( \tau \right),\mu } \right)} - \psi \left( {{\lambda ^*},\mu } \right)} \right) \leq \frac{{\bar \delta {R^2}}}{2}. \end{align}$

(21)

From Definition 1,one can get that the algorithm will converge in the region of radius \({{\bar \delta {R^2}}}/{2}\). When the iterative step is chosen appropriately,there will be further constraint for the upper bound of \(\bar \delta \). In ^[17],the theorem shows that the algorithm can converge to the optimal solution with arbitrary precision,if the following constraints are satisfied.

$\begin{align*} &\delta \left( t \right) > 0,\\[2mm] &\mathop {\lim }\limits_{t \to \infty } \delta \left( t \right) = 0,\\[2mm] & \sum\limits_{t = 0}^\infty {\delta \left( t \right) = \infty } ,\\[2mm] & \sum\limits_{t = 0}^\infty {{\delta^2}\left( t \right) < \infty }. \end{align*}$

Remark 2. The implementation of power adjustment is completed at sensor node; the update of multiplier is completed as link. For one-hop routing in a cluster,multiplier is updated at cluster head.

Remark 3. The information of multiplier \(\sum\nolimits_{l = 1}^L {{\lambda _l}} \),which is needed in the rate adjusting algorithm,is supplied by link algorithm,while the information of multiplier \(\sum\nolimits_{n = 1}^N {{\mu _n}{g_i}} \),which is needed in the power adjusting algorithm,is supplied by cluster head.

Remark 4. The information of rate,which is needed in the update of \(\lambda \),can be obtained using local information, while the information of \(\sum\nolimits_{n = 1}^{{N_n}} {{p_j}{g_j}} \),which is need in the update of \(\mu \),can be supplied by cluster head.

It is necessary to point out that there will not be any extra heavy burden of network resource,because during the operation of algorithm the exchanged information between node and link is just the computing result. All the parameters information needed in the iteration can be obtained using local information. So the distributed algorithm is suitable for wireless sensor networks. The flow chart of the algorithm is shown in Fig. 2.

Ⅳ. SIMULATIONS AND PERFORMANCE ANALYSIS

In this section,we give numerical examples for the proposed optimal algorithm by considering the wireless sensor networks as shown in Fig. 1. The simulations are executed using Matlab. The considered network environment and related parameters are as follows. There are 100 nodes placed in an interesting region of 200×200 (m²),and one base station is located at the center. We assume that each sensor node has an initial energy of 2 J,and the energy consumption model in each node is the same as ^[16]. Some other parameters in the simulation are listed in Table Ⅰ.

For the topology control of WSNs,usually there are three phases. They are cluster set-up,the phase of stable operation and cluster update. In the cluster based WSN,the change of topology is caused by energy consumption. The common analysis of clustering algorithm usually focus on the first and last phases,and pay more attention to the scale of cluster,energy consumption,lifetime and stability of topology. However,the neglect of adjustment in the phase of stable operation will result in the imbalance of energy consumption among the nodes. If the cluster head is exhausted,the cluster has to turn into the phase of cluster update. That will affect the cluster stability and lifetime of networks. The power control scheme is operated during the phase of stable operation. So the other two phases are omitted. In the phase of stable operation,we first focus on the process of rate adjustment. The adjusting curves are given in Fig. 3. One can see that the algorithm has better convergence rate.

The weighted factor introduced in (6) is used as a tradeoff utility between rate and power. For the contradiction between two performance indexes,it is necessary to balance them. We define the average rate of cluster $n$ as

$\begin{align*} \bar r = \frac{1}{{{N_n}}}\sum\limits_{i = 1}^{{N_n}} {{r_i}}. \end{align*}$

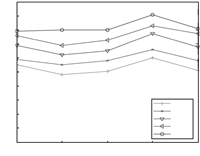
Next we evaluate the effect of weighted factor on the performance of rate. As shown in Fig. 4,one can see that the rate will be predominate in the networks' utility with the increment of $\alpha$, and the average rate also increases. However,the improvement of throughput is at the expense of energy consumption and the lifetime of network.

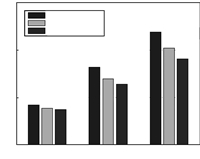
To evaluate the performance of joint optimization in terms of energy balance and lifetime prolonging,we compare the proposed scheme with some other cluster routing algorithms,LEACH and EECF. LEACH is one of the most famous clustering algorithms and is proposed by Heinzelman in MIT. EECF is an improved clustering algorithm,which focuses on how to reduce the exchanged inner information in the network and improve the convergence speed. Here we do not change the clustering rules of two algorithms,and adopt the joint optimization strategy in stable operation. The results are shown in Figs. 5 and 6. For LEACH protocol,the number of alive nodes with joint optimization is more than that of original algorithm. The difference in EECF protocol is more obvious as shown in Fig. 6. The more the alive nodes are,the longer the lifetime of network will be. It is a benefit to keep the network topology stable. With different initial energy,the average rates of cluster of three algorithms are given in Fig. 7. With same energy consumption,the average rate using joint optimization is higher than the other two. The reason is that in the joint optimization scheme,it considers both power and rate performance and approach dynamic balance. The proposed scheme can improve the throughput and reduce the energy consumption.

Ⅴ. CONCLUSIONS

Motivated by the significant role of cluster head in cluster-based WSNs,we present how to jointly allocate the power and rate of sensor node. To improve network throughput and reduce energy consumption,we formulate a novel joint optimization model with the protection for cluster head. The cost function composed of two appropriate sub-utility functions is introduced to evaluate the joint performance of rate and power. The distributed algorithm is given based on dual decomposition method and the convergence of the proposed iterative algorithm is proved analytically. Numerical results show that the performance can be improved in terms of network lifetime and throughput. Further research of the paper are as follows. First,we assume that the all the sensor nodes are fixed and the cluster heads communicate with the base station in one hop. How to extend the method in mobile and multi-hop scenario is to be addressed. Second,in the cost function,the weighted factor is given factitiously to balance two aspects of performance. It can also be regarded as a variable and it is an interesting problem to get the optimal solution in dynamic networks.

ACKNOWLEDGEMENT

The authors would like to thank anonymous reviewers for their constructive comments which helped us to improve the quality of this paper.