2. Centre de la Recherche en Automatique de Nancy(CRAN), Universite de Lorraine, Longwy 54400, France;
3. Institute of Electrical Engineering, Yanshan University, Qinhuangdao 066004, China
AS networks become ubiquitous and more and more industrial control systems are connected to open public networks,control systems are increased the risk of exposure to cyber-attacks. Control systems are vulnerable to cyber-threats,and successful attacks on them can cause serious consequences[1, 2, 3]. Therefore,the security and safety issues in controlled systems have been recently realized and they are currently attracting considerable attention[4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]. Some researchers focused on the cyber security of water systems[3, 6, 7]. Further works considered cyber-attacks on smart grid systems[4, 8, 9, 10, 12]. In order to detect as well as identify and isolate these cyber-attacks as early as possible,different detection approaches were presented. For example [13] investigated the problem of false data injection attacks against state estimation in electric power grids[14] proposed a model predictive approach for cyber-attack detection[15]. presented a stochastic cyber-attack detection scheme based on frequency-domain transformation technique[16]. considered robust $H_{\infty }$ cyber-attacks estimation for control systems[17]. proposed a detection algorithm by investigating the frequency spectrum distribution of the network traffic. References [18, 19, 20] used consensus dynamics in networked multi-agent systems including malicious agents. As far as we know,no existing literatures deal with the problem of multiple cyber-attacks. In practice,however,hackers might attempt to launch multiple attacks aiming at multiple communication channels of a control system in order to create attacks that are more stealthy and thus more likely to succeed. When a hacker launches two or more cyber-attacks against a control process,usually it is claimed that the control system suffers from multiple cyber-attacks. The fact that no research currently deals with the detection of multiple cyber-attacks on a control process motivates our research in detection of multiple cyber-attacks.
This paper deals with the problem to detect multiple stochastic cyber-attacks aiming at multiple communication channels of a control system. We present an algebraic detection approach based on the frequency-domain transformation. The basic idea is to use appropriate observers to generate residual information related to cyber-attacks. An anomaly detector for the control system under multiple stochastic cyber-attacks and stochastic disturbances is derived. The main contributions in the paper are as follows. We first propose a control system with multiple stochastic cyber-attacks that satisfy a Markovian stochastic process. In addition,we also introduce the stochastic attack models that are aiming at a specific controller command input channel or sensor measurement output channel. Second,based on the frequency-domain transformation technique and auxiliary detection tools,the error dynamics of the control system is transformed into algebraic equations. We consider possible cyber-attacks as non-zero solutions of the algebraic equations and the residuals as their constant vectors. By analyzing the ranks of the stochastic system matrix and the auxiliary stochastic system matrices,the residual information caused by attacks from different communication channel is obtained,respectively. Furthermore,based on the obtained residual information,we are able to determine the detectability of these cyber-attacks. The sufficient and necessary conditions guaranteeing that these attacks are detectable or undetectable are obtained. Finally,we provide two simulation examples to illustrate the effectiveness of our results. In Example 1,we consider a control system with stochastic noises. We detect possible stochastic cyber-attacks,which are aiming at three different controller command input channels on the actuator. In Example 2,we use the quadruple-tank process (QTP) as described in [21]. We also detect two possible cyber-attacks on the QTP. These simulation results show that the proposed attack detection approach is effective and feasible.
For convenience,we adopt the following notations: ${\rm E}\{\cdot \}$ is the mathematical expectation operator; ${\rm dim}(\cdot )$ denotes the dimension of given vector; $L_F^2([0,\infty );{{\bf{R}}^n})$ is the space of nonanticipative stochastic processes.
II. PROBLEM STATEMENTConsider the following control system with multiple stochastic cyber-attacks aiming at specific controller command input channels and sensor measurement output channels.
| \begin{align} &\dot{x}(t) = Ax(t)+B\left( u(t)+\sum_{i=1}^{n_{1}}\alpha _{i}(t)f_{i}a_{i}^{a}(t)\right) +E_{1}w(t),\nonumber \\ &x(0) = x_{0},\label{1} \nonumber \\ &y(t) = C\left( x(t)+\sum_{j=1}^{n_{2}}\beta _{j}(t)h_{j}a_{j}^{s}(t)\right) +E_{2}v(t), \end{align} | (1) |
where $x(t)\in {\bf R}^{r}$ is the state vector,$u(t)\in {\bf R}^{m}$ is the control input,$y(t)\in {\bf R}^{p}$ is the measurement output,$a_{i}^{a}(t)\in {\bf R}$,$i=1,\ldots,n_{1}$ and $a_{j}^{s}(t)\in {\bf R},$ $j=1,\ldots ,n_{2}$ denote the actuator cyber-attack aiming at the $i$-th controller command input channel and the sensor cyber-attack aiming at the $j$-th sensor measurement output channel,respectively. $A$,$B$,$C$,$E_{1}$ and $E_{2}$ are known constant matrices. $w(t)$ and $v(t)$ are stochastic noises ($w(t),v(t)\in L_{\digamma }^{2}([0,\infty );{\bf R}^{n})$). $f_{i}$ and $h_{j}$ are the attacked coefficients. $\alpha _{i}(t)$ and $\beta _{i}(t)$ are Markovian stochastic processes with the binary state ($0$ or $1$),which satisfy the following probability
| \begin{align} &{\rm E}\{\alpha _{i}(t)\} ={\rm Prob}\left\{ \alpha _{i}(t)=1\right\} =\rho _{i},\nonumber \\ &{\rm E}\{\beta _{j}(t)\} ={\rm Prob}\left\{ \beta _{j}(t)=1\right\} =\sigma _{j},\nonumber\\ &\qquad\qquad i =1,\ldots ,n_{1}\leq m,\ \ j=1,\ldots ,n_{2}\leq r.\label{0} \end{align} | (2) |
Herein,the event $\alpha _{i}(t)=1$ (or $\beta _{j}(t)=1$) shows that the $i$-th controller command input channel on the actuator (or the $j$-th sensor measurement output channel on the sensor) is subject to an actuator cyber-attack $a_{i}^{a}(t)$ (or a sensor cyber-attack $a_{j}^{s}(t)$); $% \alpha _{i}(t)=0$ (or $\beta _{j}(t)=0$) means no attack on the $i$-th (or the $j$-th)channel. $\rho _{i}\in \lbrack 0,1]$ (or $\sigma _{j}\in \lbrack 0,1]$) reflects the occurrence probability of the event that the actuator (or the sensor) of the system is subject to a cyber-attack $a_{i}^{a}(t)$ (or $a_{j}^{s}(t)$). $\alpha _{i}(t)$ and $\beta _{j}(t)$ are independent from each other,they are also independent from the stochastic noises $w(t),v(t)$ and the initial state $x_{0}.$
The control input matrix $B$ and the output state matrix $C$ are expressed as the following column vector groups,respectively
| \begin{align} &B =\left[ \begin{array}{ccccc} b_{1} & \ldots & b_{i} & \ldots & b_{m}% \end{array}% \right],\notag \\ &C =\left[ \begin{array}{ccccc} c_{1} & \ldots & c_{j} & \ldots & c_{r}% \end{array}% \right],\label{4} \end{align} | (3) |
where $b_{i}$ is the $i$-th column vector of matrix $B$ and $c_{j}$ is the $j $-th column vector of matrix $C.$ And the control input $u(t)$ and the system state $x(t)$ are written as
| \begin{align} u(t)=\left[ \begin{array}{c} u_{1}(t) \\ u_{2}(t) \\ \vdots \\ u_{m}(t)% \end{array}% \right] ,\ \ x(t)=\left[ \begin{array}{c} x_{1}(t) \\ x_{2}(t) \\ \vdots \\ x_{r}(t)% \end{array}% \right]. \label{5} \end{align} | (4) |
In order to increase the success chance of an attack and to intrude more stealthily,hackers may attempt to launch stochastic cyber-attacks aiming at one or several special communication channels of a control system. In a stochastic data denial-of-service (DoS) attack,the objective of hackers is to prevent the actuator from receiving control commands or the controller from receiving sensor measurements. Therefore,by compromising devices and preventing them from sending data, attacking the routing protocols,jamming the communication channels,flooding the communication network with random data and so on,hackers can launch a stochastic data DoS attack that satisfies Markovian stochastic processes. In a stochastic data deception attack,hackers attempt to prevent the actuator or the sensor from receiving an integrity data by sending false information $\widetilde{u}% (t)\neq u(t)$ or $\widetilde{y}(t)\neq y(t)$ from controllers or sensors. The false information includes: injection of a bias data that cannot be detected in the system,or an incorrect time of observing a measurement; a wrong sender identity,an incorrect control input or an incorrect sensor measurement. The hacker can launch these attacks by compromising some controllers or sensors or by obtaining the secret keys.
In this work,we model stochastic data DoS attacks and stochastic data deception attacks,which hackers possibly launch on a control system aiming at a specific controller command input channel or sensor measurement output channel.
1) A stochastic DoS attack preventing the actuators from receiving control command of the $i$-th control channel can be modelled as
| \begin{align} &\alpha _{i}(t) \in \left\{ 0,1\right\} ,\qquad t\geq t_{0},\ i=1,\ldots ,n_{1}\leq m, \notag \\ &f_{i} =\left[ \begin{array}{c} 0 \\ \vdots \\ 1 \\ \vdots \\ 0% \end{array}% \right] _{m\times 1} ,\label{001} \\ &a_{i}^{a}(t) =-u_{i}(t). \notag \end{align} | (5) |
2) A stochastic DoS attack preventing the sensors from receiving sensor measure of the $j$-th output channel can be modelled as
| \begin{align} &\beta _{j}(t) \in \left\{ 0,1\right\} ,\qquad t\geq t_{0},\ j=1,\ldots ,n_{2}\leq r, \notag \\ &h_{j} =\left[ \begin{array}{c} 0 \\ \vdots \\ 1 \\ \vdots \\ 0% \end{array}% \right] _{r\times 1},\label{002} \\ &a_{j}^{s}(t)=-x_{j}. \notag \end{align} | (6) |
Moreover,if the following conditions are satisfied:
| \begin{align} \sum_{i=1}^{m}\alpha _{i}(t)f_{i}a_{i}^{a}(t)=-u(t), \end{align} | (7) |
and
| \begin{align} \sum_{j=1}^{r}\beta _{j}(t)h_{j}a_{j}^{s}(t)=-x(t), \end{align} | (8) |
these stochastic attacks mentioned above completely deny the services on the actuator and on the sensors,respectively.
3) A stochastic data deception attack preventing the actuator from a correct control input of the $i$-th control channel can be modelled as
| \begin{align} &\alpha _{i}(t) \in \left\{ 0,1\right\} ,\qquad t\geq t_{0},\ i=1,\ldots ,n_{1}\leq m, \notag \\ &f_{i} =\left[ \begin{array}{c} 0 \\ \vdots \\ 1 \\ \vdots \\ 0% \end{array}% \right] _{m\times 1},\label{05} \\ &a_{i}^{a}(t) =-u_{i}(t)+d_{i}^{a}(t)\text{ or }a_{i}^{a}(t)=d_{i}^{a}(t). \notag \end{align} | (9) |
4) A stochastic data deception attack preventing the sensor from a correct sensor measurement of the $j$-th output channel can be modelled as
| \begin{align} &\beta _{j}(t) \in \left\{ 0,1\right\} ,\qquad t\geq t_{0},\ j=1,\ldots ,n_{2}\leq r, \notag \\ &h_{j} =\left[ \begin{array}{c} 0 \\ \vdots \\ 1 \\ \vdots \\ 0% \end{array}% \right] _{r\times 1},\label{051} \\ &a_{j}^{s}(t) =-x_{j}+d_{j}^{s}(t)\text{ or }a_{j}^{s}(t)=d_{j}^{s}(t),\notag \end{align} | (10) |
where $d_{i}^{a}(t)$ and $d_{j}^{s}(t)$ are deceptive data that hackers attempt to launch on the actuator and the sensor,respectively.
Now,let $T_{d_{i}^{a}y}(s)=C(sI-A)^{-1}b_{i}$ which is the transfer function from the attack $d_{i}^{a}(t)$ to output measure $y(t).$ When hackers launch a data deception attack $% a_{i}^{a}(t)=d_{i}^{a}(t)$ on the actuator to make $T_{d_{i}^{a}y}(s)=0$,a zero dynamic attack occurs on the actuator. Obviously,a zero dynamic attack is undetectable. In addition,it is not possible for a hacker to launch a zero dynamic attack on the sensor,since the transfer function from the attack $d_{j}^{s}(t)$ to output $y(t)$ is $T_{d_{j}^{s}y}(s)=c_{j}\neq 0.$
Remark 1. In the stochastic attack models (5)$-$(10),the attacked coefficients$\ f_{i}$ and $h_{j}$ are column vectors. Herein only the element in the $i$-th row is $1$ and the rest elements are $0$ in $f_{i}$,which implies that only the $i$-th control channel of a control system is attacked. Similarly,only the element in the $j$-th row is $1$ and the rest elements are $0$ in $h_{j}$,which implies that only the $j$-th output channel of a control system is attacked.
Remark 2. To attack a target,hackers may launch multiple attacks aiming at multiple communication channels so that the aggression opportunities are increased and the attack target is compromised,more stealthily and successfully. For example,in order to effectively disturb the formation control of multi-vehicle systems,a hacker could launch multiple stochastic cyber-attacks,which are respectively aiming at different communication links among these vehicles or aiming at multiple controller command input channels of a single vehicle. Obviously,the detection and isolation of multiple cyber-attacks are very important in the formation control of multi-vehicle systems. Therefore,the research on multiple cyber-attacks is significant,and requires further research.
III. MAIN RESULTSIn this section,we present the approach to the anomaly detection. We assume that the following conditions are satisfied: 1) the pair $(A,B)$ is controllable; 2) $(A,C)$ is observable. For simplification of the discussion,we ignore the influence of control inputs in the remainder of this paper because they do not affect the residual when there are no modeling errors in the system transfer matrix. Therefore,system (1) can be rewritten as follows:
| \begin{align} &\dot{x}(t) =Ax(t)+\sum_{i=1}^{n_{1}}\alpha _{i}(t)Bf_{i}a_{i}^{a}(t)+E_{1}w(t),\notag \\ &x(0) =x_{0},\label{d1}\notag \\ &y(t) =Cx(t)+\sum_{j=1}^{n_{2}}\beta _{j}(t)Ch_{j}a_{j}^{s}(t)+E_{2}v(t). \end{align} | (11) |
We set up the following anomaly detector:
| \begin{align} &\dot{\widetilde{x}}(t) =A\widetilde{x}(t)+\widetilde{B}r(t),\notag \\ &\widetilde{x}(0) =0,\label{a1}\notag \\ &r(t) =y(t)-C\widetilde{x}(t), \end{align} | (12) |
where $\widetilde{B}$ is the detector gain matrix and $r(t)$ represents the output residual.
Let $e(t)=x(t)-\widetilde{x}(t),$ then we obtain the following error dynamics:
| \begin{align} &\dot{e}(t) =\overline{A}e(t)+\sum_{i=1}^{n}\overline{F}_{i}a_{i}(t)+% \overline{E}_{1}d(t),\label{d2} \notag\\ &r(t) =Ce(t)+\sum_{i=1}^{n}\overline{H}_{i}a_{i}(t)+\overline{E}_{2}d(t), \end{align} | (13) |
with the matrices
| \begin{align} &\overline{A} =(A-\widetilde{B}C),\notag\\ &\overline{H}_{i}=\left[ \begin{array}{cc} 0 & \beta _{i}(t)Ch_{i},% \end{array}% \right],\notag \\ &\overline{F}_{i} =\left[ \begin{array}{cc} \alpha _{i}(t)Bf_{i} & -\beta _{i}(t)\widetilde{B}Ch_{i},% \end{array}% \right],\label{d3} \notag\\ &\overline{E}_{1} =\left[ \begin{array}{cc} E_{1} & -\widetilde{B}E_{2}% \end{array}% \right],\notag\\ &\overline{E}_{2}=\left[ \begin{array}{cc} 0 & E_{2}% \end{array}% \right], \end{align} | (14) |
and the vectors
\[\begin{array}{*{20}{c}} {{a_i}(t) = \left[ {\begin{array}{*{20}{c}} {a_i^a(t)}\\ {a_i^s(t)} \end{array}} \right],\quad }\\ {d(t) = \left[ {\begin{array}{*{20}{c}} {w(t)}\\ {v(t)} \end{array}} \right],} \end{array}\]where cyber-attacks $a_{i}^{a}(t)$,$a_{i}^{s}(t),$ $i=1,\ldots ,n$ and the vectors describing the attacked coefficients $f_{i},$ $h_{i},$ $i=1,\ldots ,n$ satisfy the following conditions
\begin{align*} &n \leq \max \{n_{1},n_{2}\} ,\end{align*} \begin{align*} \begin{cases} a_{n_{1}+1}^{a}(t) =a_{n_{1}+2}^{a}(t)=\cdots =a_{n}^{a}(t)=0,& n=n_{2}>n_{1} ,\\ a_{n_{2}+1}^{s}(t) =a_{n_{2}+2}^{s}(t)=\cdots =a_{n}^{s}(t)=0,& n=n_{1}>n_{2}, \end{cases} \end{align*}
and
\begin{align*} \begin{cases} f_{n_{1}+1} =f_{n_{1}+2}=\cdots =f_{n}=0,&n=n_{2}>n_{1},\\ h_{n_{2}+1} =h_{n_{2}+2}=\cdots =h_{n}=0,&n=n_{1}>n_{2}. \end{cases} \end{align*}
Before presenting the main results,we give the following definition and lemma.
Definition 1. For anomaly detector error dynamics,if a cyber-attack on a control system leads to zero output residual,then the cyber-attack is undetectable.
If $T_{dr}(s)=C(sI-\overline{A})^{-1}\overline{E}_{1}+\overline{E}_{2}$ denotes the transfer function from stochastic disturbance $d(t)$ to output residual $r(t),$ the robust stability condition of error dynamic (13) is given in term of the following lemma.
Lemma 1[16].} When all stochastic events $\alpha _{i}(t)=\beta _{i}(t)=0$ $(i=1,\ldots ,n),$ there are the following conclusions:
1) The error dynamics (13) without disturbances is asymptotically stable,if there exists a symmetric positive definite matrix $P>0$ and a matrix $% X$ such that the following linear matrix inequality (LMI) holds
| \begin{align} \Psi =A^{\rm T}P+PA-C^{\rm T}X^{\rm T}-XC+C^{\rm T}C<0. \label{b1} \end{align} | (15) |
2) The error dynamics (13) with disturbances $d(t)$ ($0\neq d(t)$ $\in$ $L_{\digamma }^{2}([0,\infty );{\bf R}^{n})$) is robustly stable,if $\left\Vert T_{dr}(s)\right\Vert _{\infty }<1$ and if there exists a symmetric positive definite matrix $P>0$ and a matrix $X$ such that the following LMI holds
| \begin{align} \left[ \begin{array}{ccc} \Psi & PE_{1} & -XE_{2}+C^{\rm T}E_{2} \\ \ast & -I & 0 \\ \ast & \ast & -I+E_{2}^{\rm T}E_{2}% \end{array}% \right] <0. \label{b} \end{align} | (16) |
When the LMIs above are solvable,the detector gain matrix is given by $\tilde B = {P^{ - 1}}X.$
A. Algebraic Detection Scheme for Multiple Stochastic Cyberattacks Aiming at Multiple Communication ChannelsIn this section,using the frequency-domain description of the system,we transform the error dynamics (13) into the following equation:
| \begin{align} Q(s)X(s)=B(s), \end{align} | (17) |
where
\begin{array}{*{20}{c}} {Q(s) = \left[ {\begin{array}{*{20}{c}} {\bar A - sI}&{{{\bar F}_1}}& \ldots &{{{\bar F}_n}}&{{{\overline E }_1}}\\ C&{{{\bar H}_1}}& \ldots &{{{\bar H}_n}}&{{{\bar E}_2}} \end{array}} \right],}\\ {X(s) = \left( {\begin{array}{*{20}{c}} {e(s)}\\ {{a_1}(s)}\\ \vdots \\ {{a_n}(s)}\\ {d(s)} \end{array}} \right),\;\;B(s) = \left( {\begin{array}{*{20}{c}} 0\\ {r(s)} \end{array}} \right).} \end{array}
Further,in order to obtain effective results,we introduce the mathematical expectation of the stochastic matrix $Q(s)$ as follows:
| \begin{align} {\rm E}(Q(s))=\left[ \begin{array}{ccccc} \overline{A}-sI & {\rm E}(\overline{F}_{1}) & \ldots & {\rm E}(\overline{F}_{n}) & \overline{{ E}}_{1} \\ C & {\rm E}(\overline{H}_{1}) & \ldots & {\rm E}(\overline{H}_{n}) & \overline{{ E}}_{2}% \end{array}% \right], \end{align} | (18) |
where
\begin{array}{*{20}{c}} {{\rm{E}}({{\bar F}_i}) = \left[ {\begin{array}{*{20}{c}} {{\rho _i}B{f_i}}&{ - {\sigma _i}\tilde BC{h_i}} \end{array}} \right],}\\ {{\rm{E}}({{\bar H}_i}) = \left[ {\begin{array}{*{20}{c}} 0&{{\sigma _i}C{h_i}} \end{array}} \right],\qquad \qquad \;\;i = 1, \ldots ,n.} \end{array}
Then the system (17) can be described as
| \begin{align} {\rm E}(Q(s))X(s)=B(s), \end{align} | (19) |
and the equation (19) can be rewritten as
\begin{align*} {\rm E}(Q(s))X(s)=\sum_{i=1}^{n}{\rm E}(\widetilde{Q}_{i}(s))X_{i}(s)=\sum_{i=1}^{n}B_{i}(s), \end{align*}
where
\begin{align*} &{\rm E}(\widetilde{Q}_{i}(s)) =\left[ \begin{array}{ccc} \dfrac{\overline{A}-sI}{n} & {\rm E}(\overline{F}_{i}) & \dfrac{\overline{E}_{1}}{n} \\[3mm] \dfrac{\overline{C}}{n} & {\rm E}(\overline{H}_{i}) & \dfrac{\overline{{ E}}_{2}}{n}% \end{array}% \right] ,\\[2mm] &X_{i}(s)=\left( \begin{array}{c} e(s) \\[1mm] a_{i}(s) \\[1mm] d(s)% \end{array}% \right),\\[2mm] &B_{i}(s)=\left( \begin{array}{c} 0 \\ r_{i}(s)% \end{array}% \right) ,\\[2mm] &r(s)=\sum_{i=1}^{n}r_{i}(s). \end{align*}
Consider the following stochastic matrix:
\begin{align*} {\rm E}(Q_{i}(s))=\left[ \begin{array}{ccc} \overline{A}-sI & {\rm E}(\overline{F}_{i}) & \overline{{ E}}_{1} \\[2mm] C & {\rm E}(\overline{H}_{i}) & \overline{{ E}}_{2}% \end{array}% \right]. \end{align*}
Since ${\rm rank}{\rm E}(\widetilde{Q}_{i}(s))={\rm rank}{\rm E}(Q_{i}(s)),$ we introduce the following auxiliary error dynamics
| \begin{align} &\dot{e}(t) =\overline{A}e(t)+\overline{F}_{i}a_{i}(t)+\overline{E}% _{1}d(t),\notag \\ &r(t) =Ce(t)+\overline{H}_{i}a_{i}(t)+\overline{{ E}}_{2}d(t) ,\label{d4}\notag \\ &\qquad\qquad\qquad\qquad\qquad\quad\ i =1,\ldots ,n, \end{align} | (20) |
and the auxiliary stochastic equations
| \begin{align} {\rm E}(Q_{i}(s))X_{i}=B_{i}(s),\ \ \ i=1,\ldots ,n. \label{I} \end{align} | (21) |
Remark 3. Here,since the matrices $\overline{F}_{i}$ and $% \overline{H}_{i}$ include the stochastic parameters $\alpha _{i}(t)$ and $% \beta _{i}(t)$,the system matrix $Q(s)$ correspondingly includes these stochastic parameters,and ${\rm E}(Q(s))$ and ${\rm E}(Q_{i}(s))$ include stochastic probabilities $\rho _{i}$ and $\sigma _{i}$ as well,which take values in $% \left[0,1\right] $. Therefore,they are stochastic matrices.
Remark 4. In this work,we introduce the auxiliary mathematical ``tools'' (20) and (21). The auxiliary error dynamics (20) represents the fact that the control system is only subjected to a stochastic cyber-attack $% a_{i}(t)$ on the $i$-th communication channel. Applying the auxiliary equation (21),we can obtain the information of residual $r_{i}(t)$ that is caused by the cyber-attack $a_{i}(t)$. In addition,the detector gain matrix $\widetilde{B}$ can be determined according to Lemma 1.
Now,applying the rank of the stochastic matrix,we obtain the following theorem.
Theorem 1. For system (11),we assume that all of these stochastic matrices ${\rm E}(Q(s))$ and ${\rm E}(Q_{i}(s))$ $(i=1,\ldots,n)$ have full column normal rank. All of these cyber-attacks $a_{i}(s)$ $(i=1,\ldots ,n,$ $% (0\neq a_{i}(s)\in \overline{G}))$ when $s=z_{0}$ are undetectable,if and only if there exists $z_{0}\in$ ,such that
| \begin{align} {\rm rank}{\rm E}(Q(z_{0}))<{\rm dim}(X(z_{0})),\label{b4} \end{align} | (22) |
and
| \begin{align} {\rm rank}{\rm E}(Q_{i}(z_{0}))<{\rm dim}(X_{i}(z_{0})),\ \ i=1,\ldots ,n. \end{align} | (23) |
Herein $\overline{G}$ is a set of undetectable cyber-attacks.
Proof. (If) Assume that there exists $z_{0}\in {\bf C}$ such that conditions (22) and (23) hold for all $a_{i}(z_{0})$ $\in \overline{G},$ it becomes obvious that $z_{0}$ is an invariant zero[22] of the detector error system (13) and the auxiliary system (20). Then all of the equations in (19) and (20) are homogeneous,i.e.,$B(z_{0})=0\ $and $B_{i}(z_{0})=0.$ Therefore,the output residual $% r_{i}(z_{0})=0$,$i=1,\ldots ,n$,and $r(z_{0})$ $=$ $\sum_{i=1}^{n}r_{i}(z_{0})=0$ as well. By Definition 1,all of these cyber-attacks $a_{i}(s),$ $i\ldots ,n$ when $% s=z_{0}$ are undetectable.
(Only if) Assume that all of these cyber-attacks $a_{i}(s),$ $i$ $=$ $1,\ldots,n$ when $s=z_0$ are undetectable,then there must exist a $z_{0}\in {\bf C}$ such that the residual $r_{i}(z_{0})=0$ and $r(z_{0})$ $=$ $\sum_{i=1}^{n}r_{i}(z_{0})=0.$ Therefore,all of the equations in (19) and (21) are homogeneous. If we assume that all of matrices ${\rm E}(Q(z_{0}))$ and ${\rm E}(Q_{i}(z_{0}))$ have full column rank,then all of these homogeneous equations have and only have one zero solution. However,this contradicts with the conditions that
\begin{align*} X\left\vert _{s=z_{0}}\right. \neq 0,\quad X_{i}\left\vert _{s=z_{0}}\right. \neq 0,\ i=1,\ldots ,n \end{align*}are solutions to (19) and (21),respectively. Therefore the assumptions are false,only conditions (22) and (23) are true.
Theorem 2. For system (11),we assume that all of stochastic matrices ${\rm E}(Q(s))\ $and ${\rm E}(Q_{i}(s))$ $(i=1,\ldots,n)$ have full column normal rank. All of these cyber-attacks $a_{i}(s)$ $(i=1$,$\ldots $,$n$,$% (0\neq a_{i}(s)\in G))$ are detectable,if and only if the following conditions always hold for any $z_{0}\in {\bf C}$:
| \begin{align} {\rm rank}{\rm E}(Q(z_{0}))={{\rm dim}}(X(z_{0})), \end{align} | (24) |
and
| \begin{align} {\rm rank}{\rm E}(Q_{i}(z_{0}))={{\rm dim}}(X_{i}(z_{0})),\ \ i=1,\ldots ,n. \end{align} | (25) |
Herein $G$ is a set of detectable cyber-attacks.
Proof. (If) Assuming that conditions (24) and (25) always hold for any $z_{0}\in {\bf C}$,it is obvious that the stochastic matrices ${\rm E}(Q(z_{0}))$ and ${\rm E}(Q_{i}(z_{0}))$ $(i=1,\ldots,n)$ have full column rank. Then the equation
| \begin{align} {\rm E}(Q(z_{0}))X(z_{0})=B(z_{0}), \end{align} | (26) |
and the auxiliary stochastic equations
| \begin{align} {\rm E}(Q_{i}(z_{0}))X_{i}=B_{i}(z_{0}),\ \ i=1,\cdots ,n \label{n6} \end{align} | (27) |
have one and only one solution. In the following,we proof by contradiction. Assume that residual $r(z_{0})=0$ and $r_{i}(z_{0})=0$,$i$ $=$ $1,\ldots ,n$,then equations (26) and (27) has one and only one zero solution,i.e.,
\begin{align*} X\left\vert _{s=z_{0}}\right. =0,\quad X_{i}\left\vert _{s=z_{0}}\right. =0,\ i=1,\ldots ,n. \end{align*}However,this violates the given condition $0\neq a_{i}(z_{0})\in G$,i.e.,
\begin{align*} X\left\vert _{s=z_{0}}\right. \neq 0,\quad X_{i}\left\vert _{s=z_{0}}\right. \neq 0,\ i=1,\ldots ,n. \end{align*}Therefore $r(z_{0})\neq 0$ and $r_{i}(z_{0})\neq 0$,$i=1,\ldots ,n,$ these cyber-attacks $a_{i}(s)$ $(0\neq a_{i}(s)\in G)$,$i=1,\ldots ,n,$ for any $ s$ $=$ $z_{0}$ are detectable.
(Only if) Assume that there exists a $z_{0}\in {\bf C}$ which satisfies conditions (22) and (23). Since all of the stochastic matrices ${\rm E}(Q(s))\ $and ${\rm E}(Q_{i}(s))$ $(i=1,\ldots,n)$ have full column ranks,according to Theorem 1,these cyber-attacks $a_{i}(s),$ $i=1,\ldots ,$ $n $ are undetectable as $s=z_{0}$. However,this is in contradiction with the given condition that all of these cyber-attacks $a_{i}(s),$ $i$ $=1,\ldots ,n$ are detectable for any $s=z_{0}$. Therefore the assumption is false,only
\begin{align*} {\rm rank}{\rm E}(Q(z_{0}))={{\rm dim}}(X(z_{0})), \end{align*}and
\begin{align*} {\rm rank}{\rm E}(Q_{i}(z_{0}))={{\rm dim}}(X_{i}(z_{0})),\ \ i=1,\ldots ,n \end{align*}are true.
Furthermore,we can obtain the following corollary according to Theorem 1 and Theorem 2.
Corollary 1. For system (11),assume that all of stochastic matrices ${\rm E}(Q(s))$ and ${\rm E}(Q_{i}(s))$ $(i=1,\ldots,n)$ have full column normal rank. If there exists $z_{0}\in {\bf C}$,such that
| \begin{align} {\rm rank}{\rm E}(Q(z_{0}))<{{\rm dim}}(X(z_{0})), \end{align} | (28) |
then there are the following conclusions.
1) The cyber-attack $a_{i}(z_{0})$ $(0\neq a_{i}(s)\in G)$ is detectable,if and only if
| \begin{align} {\rm rank}{\rm E}(Q_{i}(z_{0}))={{\rm dim}}(X_{i}(z_{0})). \end{align} | (29) |
2) The cyber-attack $a_{j}(z_{0})$ $(0\neq a_{j}(s)\in G)$ is undetectable,if and only if
| \begin{align} {\rm rank}{\rm E}(Q_{j}(z_{0}))<{{\rm dim}}(X_{j}(z_{0})). \end{align} | (30) |
In this section,we provide two simulation examples to illustrate the effectiveness of our results. In Example 1,we consider a control system under three stochastic cyber-attacks and a stochastic noise. We detect two possible stochastic data DoS attacks and a possible stochastic data deception attack,which are aiming at three controller command input channels on the actuator. In Example 2,we use the laboratory process as presented in [21],which consists of four interconnected water tanks. We will also detect possible cyber-attacks on QTP controlled through a wireless communication network.
Example 1. Consider the following system with a stochastic noise $% w(t)$
| \begin{align} &\dot{x}(t) =Ax(t)+Bu(t)+E_{1}w(t),\nonumber \\ &x(0) =x_{0},\label{ss} \\ &y(t) =Cx(t),\nonumber \end{align} | (31) |
and with the following parameters:
\begin{align*} &A =\left[ \begin{array}{ccccc} -0.8 & 0 & 0.1 & 0 & 0 \\ 0 & -0.2 & 0 & -0.1 & 0 \\ 0 & 0 & -0.4 & 0 & 0 \\ 0 & 0 & 0 & -0.3 & 0 \\ 0.2 & 0 & 0.1 & 0 & -0.5% \end{array}% \right],\\ &B =\left[ \begin{array}{ccc} 0.03 & 0 & 0.3 \\ 0 & 0.04 & 0 \\ 0 & -0.08 & 0.45 \\ -0.21 & 0 & 0.1 \\ 0.09 & 0 & 0% \end{array}% \right],\\ &E_{1} =\left[ \begin{array}{c} 0.09 \\ -0.01 \\ 0.04 \\ -0.07 \\ 0.06% \end{array}% \right] ,\quad C=\left[ \begin{array}{ccccc} 0.5 & 0 & 0 & 0 & 0 \\ 0 & 0.5 & 0 & 0 & 0 \\ 0 & 0 & 0.5 & 0 & 0 \\ 0 & 0 & 0 & 0.5 & 0% \end{array}% \right]. \end{align*}Assume that it is subjected to two stochastic data DoS attacks and a stochastic data deception attack on the actuator aiming at three controller command input channels,i.e.,
| \begin{align} &\alpha _{1}(t) \in \left\{ 0,1\right\} ,\quad t\geq t_{0},\nonumber \\ &f_{1} =\left[ \begin{array}{c} 1 \\ 0 \\ 0% \end{array}% \right] ,\label{s1} \\ &a_{1}^{a}(t) =-u_{1}(t),\nonumber \end{align} | (32) |
and
| \begin{align} &\alpha _{2}(t) \in\left\{ 0,1\right\} ,\quad t\geq t_{0},\nonumber \\ &f_{2} =\left[ \begin{array}{c} 0 \\ 1 \\ 0% \end{array}% \right] ,\label{s2} \\ &a_{2}^{a}(t) =-u_{2}(t)+b_{2}^{a}(t),\nonumber\end{align} | (33) |
and
| \begin{align} &\alpha _{3}(t) \in \left\{ 0,1\right\} ,\quad t\geq t_{0} ,\nonumber \\ &f_{3} =\left[ \begin{array}{c} 0 \\ 0 \\ 1% \end{array}% \right],\\ &a_{3}^{a}(t) =-u_{3}(t). \nonumber \end{align} | (34) |
As mentioned before,we ignore the control input,since it does not affect the residual.
By applying Lemma 1,the robust detector gain matrix can be obtained as follows:
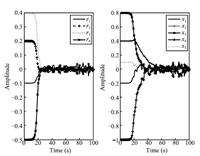
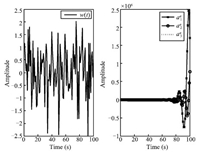
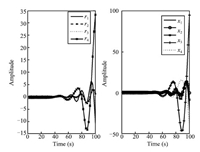
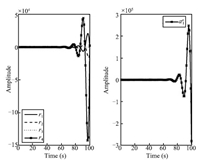
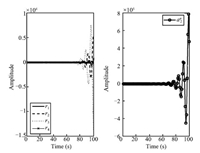
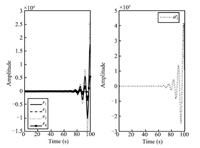
\begin{align*} \widetilde{B}=\left[ \begin{array}{cccc} 0.6316 & 0 & 0.0826 & 0 \\ 0 & 2.7474 & 0 & -0.6078 \\ 0.0961 & 0 & 1.2444 & 0 \\ 0 & -0.6325 & 0 & 1.7707 \\ 0.0251 & 0 & 0.0304 & 0% \end{array}% \right]. \end{align*}Set the initial conditions as $\widetilde{x}(0)=[0,0,0,0]^{\rm T}$ and $ x(0)$ $=$ $[-0.2,0.4,0.8,-1,0.1]^{\rm T}.$ When the stochastic events $\alpha _{1}(t)$ $=$ $\alpha _{2}(t)=\alpha _{3}(t)=0$ occur,the system is not under any cyber-attacks. Fig. 1 displays the time responses of the residual and the system state under stochastic noise $w(t)$ only,which shows that the system is robustly stable. When the stochastic events $\alpha _{1}(t)=\alpha _{2}(t)=\alpha _{3}(t)=1$ occur,the system is under multiple cyber-attacks. We take the attack probabilities $\rho _{1}=\rho _{2}=0.8$ and $\rho _{3}=0.5,$ the stochastic matrix ${\rm rank}({\rm E}(Q(s)))=9,$ and $ {\rm rank}({\rm E}(Q(z_{0})))=9,$ ${\rm rank}({\rm E}(Q_{i}(z_{0})))$ $=7$ $(i=1,2,3),$ which shows that ${\rm rank}({\rm E}(Q(z_{0}))),$ ${\rm rank}({\rm E}(Q_{i}(z_{0})))$ $(i=1,2,3)$ have always full column rank for any $z_{0}.$ According to Theorem 2,the three attacks are detectable. Fig. 2 displays the noise signal and the attack signals,while Fig. 3 shows the time responses of the residual and the system state under three attacks and noise. Fig. 4,Fig. 5 and Fig. 6 give the time responses of the residual under the attack $a_{1}^{a}(t)$,$a_{2}^{a}(t)$ and $% a_{3}^{a}(t)$,respectively. Simultaneously,they show the corresponding attack signals. The simulation results underline that these cyber-attacks can be effectively detected if the conditions in Theorem 2 are satisfied.
|
Download:
|
| Fig. 1. The time responses of the residual and the system state under the noise. | |
|
Download:
|
| Fig. 2. The noise signal and the attack signals. | |
|
Download:
|
| Fig. 3. The time responses of the residual and the system state under three attacks and noise. | |
|
Download:
|
| Fig. 4. The time responses of the residual under attack $a_{1}^{a}(t)$ and the attack signal $a_{1}^{a}(t)$. | |
|
Download:
|
| Fig. 5. The time responses of the residual under attack $a_{2}^{a}(t)$ and the attack signal $a_{2}^{a}(t)$. | |
|
Download:
|
| Fig. 6. The time responses of the residual under attack $a_{3}^{a}(t)$ and the attack signal $a_{3}^{a}(t)$. | |
Example 2. Consider the model of the QTP in [21].
| \begin{align} &\dot{x} =Ax+Bu,\label{q1} \\ &y=Cx,\nonumber \end{align} | (35) |
with the following parameters:
\begin{align*} &A =\left[ \begin{array}{cccc} -0.0158 & 0 & 0.0256 & 0 \\ 0 & -0.0109 & 0 & 0.0178 \\ 0 & 0 & -0.0256 & 0 \\ 0 & 0 & 0 & -0.0178% \end{array}% \right],\\ &C=\left[ \begin{array}{cccc} 0.5 & 0 & 0 & 0 \\ 0 & 0.5 & 0 & 0% \end{array}% \right],\\ &B =\left[ \begin{array}{cc} 0.0482 & 0 \\ 0 & 0.0350 \\ 0 & 0.0775 \\ 0.0559 & 0% \end{array}% \right].\\ \end{align*}Assume that it is subjected to two stochastic data deception attacks on the actuator,i.e.,
| \begin{align} &\alpha _{1}(t) \in \left\{ 0,1\right\} ,\quad t\geq t_{0},\nonumber \\ &f_{1} =\left[ \begin{array}{c} 1 \\ 0% \end{array}% \right] ,\label{s3} \\ &a_{1}^{a}(t) =b_{1}^{a}(t),\nonumber \end{align} | (36) |
and
| \begin{align} &\alpha _{2}(t) \in \left\{ 0,1\right\} ,\quad t\geq t_{0},\nonumber \\ &f_{2} =\left[ \begin{array}{c} 0 \\ 1% \end{array}% \right],\label{s4} \\ &a_{2}^{a}(t) =b_{2}^{a}(t). \nonumber \end{align} | (37) |
The detector gain matrix can be obtained as follows:
\begin{align*} \widetilde{B}=\left[ \begin{array}{cc} 0.7852 & 0 \\ 0 & 0.4766 \\ 2.7432 & 0 \\ 0 & 1.4367% \end{array}% \right], \end{align*}We set the initial conditions as $\widetilde{x}(0)=[0,0,0,0]^{\rm T}$ and $ x(0)$ $=$ $[0.1,-0.4,-0.1,0.5]^{\rm T}.$ When the stochastic events $\alpha _{1}(t)$ $=$ $\alpha _{2}(t)=0$ occur,Fig. 7 visualizes that the system (35) is asymptotically stable. When the stochastic events $\alpha _{1}(t)$ $=$ $\alpha _{2}(t)$ $=$ $1$ occur and the attack probabilities are $\rho _{1}=0.8,$ $\rho _{2}$ $=$ $0.5$,we have stochastic matrix ${\rm rank}({\rm E}(Q(s)))=6,$ however,there exists a $ z_{0}=0.0127$ such that ${\rm rank}({\rm E}(Q(z_{0})))=5$ and ${\rm rank}({\rm E}(Q_{i}(z_{0})))=5$ $ (i=1,2)$. Aiming at two different control channels,it is possible for the hacker to launch two stochastic data deception attacks as follows:
\begin{align*} &b_{1}^{a}(t) =-1.074{\rm e}^{0.0127t},\\[2mm] &b_{2}^{a}(t) ={\rm e}^{0.0127t}, \end{align*}
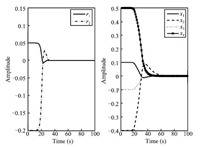
|
Download:
|
| Fig. 7. The time responses of the residual and the system state without attacks. | |
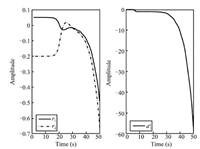
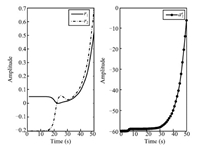
such that the transfer function from attacks to residual is zero. Therefore,it is difficult to detect these stealthy attacks. Fig. 8 displays the time responses of the residual and the system state under the two attacks $a_{1}^{a}(t)$ and $a_{2}^{a}(t)$,which shows that these attacks when $s=z_{0}=0.0127$ could not be detected by original model. However,applying the auxiliary tools (20),(21) and according to Corollary 1,these attacks can also be detected. Fig. 9 displays the attack signal $a_{1}^{a}(t)$ and the responses of the residual under this attack. Fig. 10 shows the attack signal $a_{2}^{a}(t)$ and the responses of residual under this attack. Obviously,applying Corollary 1,the two stochastic data deception attacks can be detected effectively.
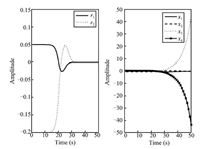
|
Download:
|
| Fig. 8. The time responses of the residual and the system state under attacks $a_{1}^{a}(t)$ and $a_{2}^{a}(t)$. | |
|
Download:
|
| Fig. 9. The time responses of residual under the attack $a_{1}^{a}(t)$ and the attack signal $a_{1}^{a}(t)$. | |
|
Download:
|
| Fig. 10. The time responses of residual under the attack $a_{2}^{a}(t)$ and the attack signal $a_{2}^{a}(t)$. | |
This paper presents a cyber-attack detection approach for control systems under multiple stochastic cyber-attacks and disturbances. The proposed problem is significant in practice,because hackers might launch multiple attacks aiming at one target so that the aggression opportunities are increased and the attack target can be compromised,more stealthily and successfully. For example,the hacker is able to simultaneously launch DoS attacks,deception attacks and replay attacks that are respectively aiming at different communication channels of a control system. The main work here is focused on novel cyber-attack detection schemes that allow the detection of multiple stochastic attacks in order to protect control systems against a wide range of possible attack models. We give two simulation examples the results of which demonstrate that the detection approaches proposed in this paper are feasible and effective.
| [1] | Bier V, Oliveros S, Samuelson L. Choosing what to protect:strategic defensive allocation against an unknown attacker. Journal of Public Economic Theory, 2007, 9(4):563-587 |
| [2] | Amin S, Schwartz G A, Sastry S S. Security of interdependent and identical networked control systems. Automatica, 2013, 49(1):186-192 |
| [3] | Slay J, Miller M. Lessons learned from the Maroochy water breach. Critical Infrastructure Protection, 2007, 253:73-82 |
| [4] | Andersson G, Esfahani P M, Vrakopoulou M, Margellos K, Lygeros J, Teixeira A, Dan G, Sanderg H, Johansson K H. Cyber-security of SCADA systems. Session:Cyber-Physical System Security in a Smart Grid Environment, 2011. |
| [5] | Mo Y L, Sinopoli B. False data injection attacks in control systems. In:Proceedings of the 1st Workshop on Secure Control Systems. Stockholm, Sweden, 2010. |
| [6] | Amin S, Litrico X, Sastry S, Bayen A M. Cyber security of water SCADA systems:(I) analysis and experimentation of stealthy deception attacks. IEEE Transactions on Control Systems Technology, 2013, 21(5):1963-1970 |
| [7] | Eliades D G, Polycarpou M M. A fault diagnosis and security framework for water systems. IEEE Transactions on Control Systems Technology, 2010, 18(6):1254-1265 |
| [8] | Metke A R, Ekl R L. Security technology for smart grid networks. IEEE Transactions on Smart Grid, 2010, 1(1):99-107 |
| [9] | Sridhar S, Hahn A, Govindarasu M. Cyber-physical system security for the electric power grid. Proceedings of the IEEE, 2012, 100(1):210-224 |
| [10] | Mohsenian-Rad A H, Leon-Garcia A. Distributed internet-based load altering attacks against smart power grids. IEEE Transactions on Smart Grid, 2011, 2(4):667-674 |
| [11] | Sardana A, Joshi R C. Dual-level attack detection and characterization for networks under DDoS. In:Proceedings of the 2010 International Conference on Availability, Reliability and Security. Krakow:IEEE, 2010. 9-16 |
| [12] | Weimer J, Kar S, Johansson K H. Distributed detection and isolation of topology attacks in power networks. In:Proceedings of the 2012 HiCoNS012. Beijing, China, 2012. 17-18 |
| [13] | Liu Y, Reiter M K, Ning P. False data injection attacks against state estimation in electric power grids. In:Proceedings of the 2009 ACM Conference on Computer and Communications Security. Chicago, IL, USA:ACM, 2009. 21-32 |
| [14] | Rosich A, Voos H, Li Y M, Darouach M. A model predictive approach for cyber-attack detection and mitigation in control systems. In:Proceedings of the 52nd Annual Conference on Decision and Control. Firenze:IEEE, 2013. 6621-6626 |
| [15] | Li Y M, Voos H, Rosich A, Darouach M. A stochastic cyber-attack detection scheme for stochastic control systems based on frequencydomain transformation technique. In:Proceedings of the 8th International Conference on Network and System Security. Xi'an, China:Springer, 2014. 209-222 |
| [16] | Li Y M, Voos H, Darouach M. Robust H∞ fault estimation for control systems under stochastic cyber-attacks. In:Proceedings of the 33rd Chinese Control Conference. Nanjing, China:ORBilu, 2014. 3124-3129 |
| [17] | Hashim F, Kibria M R, Jamalipour A. Detection of DoS and DDoS attacks in NGMN using frequency domain analysis. In:Proceedings of the 14th Asia-Pacific Conference on Communications. Tokyo:IEEE, 2008. 1-5 |
| [18] | Sundaram S, Hadjicostis C N. Distributed function calculation via linear iterative strategies in the presence of malicious agents. IEEE Transactions on Automatic Control, 2011, 56(7):1495-1508 |
| [19] | Teixeira A, Sandberg H, Johansson K H. Networked control systems under cyber attacks with applications to power networks. In:Proceedings of the 2010 American Control Conference. Baltimore, MD:IEEE, 2010. 3690-3696 |
| [20] | Pasqualetti F, Bichi A, Bullo F. Consensus computation in unreliable networks:a system theoretic approach. IEEE Transactions on Automatic Control, 2012, 57(1):90-104 |
| [21] | Johansson K H. The quadruple-tank process:a multivariable laboratory process with an adjustable zero. IEEE Transactions on Control Systems Technology, 2000, 8(3):456-465 |
| [22] | Zhou K M, Doyle J C, Glover K. Robust and Optimal Control. Upper Saddle River, NJ, USA:Prentice-Hall, Inc., 1996. |
 2015, Vol.2
2015, Vol.2 


