In recent years,growing attention has been attracted in studying the consensus problem due to a broad application of multi-agent systems,including automatic control[1], distributed estimation[2] and flocking[3],etc. Generally speaking,consensus means that several autonomous agents reach an agreement regarding a certain quantity of interest. Currently,many results on consensus have been obtained. For the Vicsek's model[4],where all the agents moved in the plane at the same speed but with different headings,its theoretical explanation for the consensus behavior was provided in [5]. Given a time-varying interconnection topology,[6] investigated a group of autonomous agents tracking an active leader by constructing a neighbor-based state-estimation rule. The necessary and sufficient condition on consensus for general discrete-time linear systems was given in [7].
Delay effect on the convergence of consensus is an important issue to be considered. Naturally,the communication delay appearing in the network hinders the information being transmitted from one agent to another[8]. So far,many researchers have studied the effect of communication delay on agents' consensus behavior. It was shown in [9] that single-integrator agents subjected to constant communication delay can achieve consensus if and only if the delay is bounded by a maximum. Given a directed and dynamically changing topology,[10] investigated the effect of communication delay that only affected the actually transmitted information on consensus. Reference [11]provided a necessary and sufficient condition to guarantee quasi-consensus and consensus with the distributed delay in the control input. Assuming that the agent dynamics is at most polynomially unstable,consensus for high-order linear multi-agent systems with delays in both the communication and input was studied in [12]. To the best of our knowledge,the relevant results in the context of discrete-time agents are rare since delay effects significantly complicate the problem. For the scalar agent dynamics that is critically unstable,[13]considered the consensus of multi-agent systems with communication delay. Reference [14] studied the existence of maximum delay margin of input delay for the general scalar discrete-time agents to achieve consensus. Under the assumption that neighbors' measured output information can be received by agents,consensus problem of the network with communication delay was studied in [15]. A constrained consensus problem requiring every agent to lie in a closed convex set was addressed in [16] over the network with communication delay. Provided that all eigenvalues of the system matrix were in the closed unit disc,[17]investigated the consensus of high-order multi-agent systems in the network with constant communication delay.
In this paper,we investigate the influences of two kinds of communication delays on consensus for unstable discrete-time multi-agent systems. If the delay only affects the relative information that is transmitted,the methods used in [13] and [17] are unavailable due to the system is unstable. The technique in [14] cannot work when the delay is much large. On the other hand, in case that the communication delay only influences the actually transmitted information,the frequency-domain approach used in [13] is helpless to the time-varying delay.
The main contribution of this paper are twofold. First,for any large yet bounded communication delay that affects the relative state information,consensus condition is given under the assumption that the network topology is exactly known. Second,if the delay only influences the actually transmitted information,a sufficient condition related to agent dynamics and network topology is shown for any large yet bounded delay to achieve consensus,and especially the delay in this case is allowed to be unknown and time-varying.
The remainder of this paper is organized as follows. In Section Ⅲ, some preliminaries of the algebraic graph theory are presented. The consensus problem to be studied is formulated in Section Ⅲ. In Section Ⅳ,consensus analysis of multi-agent networks with two kinds of communication delays are respectively presented in detail. Following that,Section V provides two simulation examples. Finally, conclusions are reported in Section VI.
The following notations will be used throughout this paper. Symbols R and ${{\rm{Z}}^{\rm{ + }}}$ respectively denote the sets of real numbers and positive integers. For any positive integer $N \in {{\bf{Z}}^ + }$,let $N: = \{ 1,2, \cdots ,N\} $ and ${I_N}$ be an identity matrix with dimension $N \times N$. Notation ${\rm{diag}}\{ {a_1},{a_2}, \cdots ,{a_N}\} $ denotes a diagonal matrix. Given that ${{\bf{1}}_N}$ is an $N$ dimensional vector with all ones and $\|\cdot\|$ is the Euclidean norm. For a scalar $r >0$,let ${C_r}$ represent the Banach space of continuous-time scalar functions mapping the interval $\{ - r, - r + 1, \cdots ,0\;\} $ into R.
Ⅲ. PRELIMINARIESIn this section,a brief introduction to the algebraic graph theory is provided.
Let $g = (V,\varepsilon ,A)$ be a weighted undirected network of order $N$,where $V = \{ 1,2, \cdots ,N\} $ is the set of nodes; $\varepsilon = V \times V$ is the set of edges and $A = [{a_{ij}}] \in {\bf{R}}\{ N \times N\} $ is the weighted adjacency matrix with symmetric nonnegative elements. Assume ${a_{ij}} > 0$ if and only if $(i,j){\rm{ }} \in \varepsilon $,i.e.,information can be exchanged between nodes $i$ and $j$. Moreover,suppose $a_{ii}=0$ for all $i \in V$. An undirected graph $G$ is connected if there exists a path between any pair of distinct nodes $i$ and $j{\mkern 1mu} (j \in V)$. The degree of node $i$ is defined as ${d_i}: = \sum _{j = {1^{aij}}}^N$and we introduce an $N \times N$ diagonal matrix $D = {\rm{diag}}\{ {d_1}, \cdots ,{d_N}\} $ as the degree matrix of $G$. Then the Laplacian matrix of $G$ is defined as${L_G}: = D - A$. Obviously,matrix ${L_G}$ is symmetric and ${{\bf{1}}_N}$ is its eigenvector corresponding to eigenvalue 0. If $G$ is connected,all the eigenvalues of ${L_G}$ are positive except one 0 eigenvalue and can be written as $0 = {\lambda _1} < {\lambda _2} \le \cdots \le {\lambda _N}.$ In addition,the eigenratio $\frac{{{\lambda _2}}}{{{\lambda _N}}}$ is an important factor[7,18],and a larger eigenratio corresponds to a better synchronizability of the underlying communication graph. If every node can directly communicate with other nodes in the network,i.e.,$(i,j) \in {\rm{ }}\varepsilon $ for $\forall i \ne j$,then the graph is called complete. Especially,the eigenratio $\frac{\lambda_{2}}{\lambda_{N}}=1$ in the complete case.
Ⅲ. PROBLEM STATEMENTIn this paper,assume all the agents considered have the following dynamics
| ${x_i}(k + 1) = a{x_i}(k) + b{u_i}(k),{\mkern 1mu} i = 1,2, \cdots ,N,$ | (1) |
where $x_{i}(k)\in \textbf{R}$ and $u_{i}(k) \in \textbf{R}$ are the state and control input of agent $i$, respectively. The coefficients satisfy $a\in \textbf{R}, b\in \textbf{R}$ and $b\neq 0$. In addition, assume $x_{i}(0)$ are known initial values.
Regarding the above $N$ agents as nodes in a network,the information flow between two agents can be regarded as a path between the nodes. Thus,the interconnection topology in multi-agent systems can be conveniently captured by an undirected graph $G = (V,\varepsilon ,A)$ with $V = \{ 1,2, \cdots ,N\;\} $ and $A = [{a_{ij}}] \in {{\bf{R}}^{N \times N}}$
Note that the communication delay is common in network control. Let $d \in {{\bf{Z}}^ + }$ denote the delay during the information communication. Making use of the relative state information,the commonly used protocol[9,,17] is described as
| ${u_i}(k) = \frac{{{k_1}}}{b}\sum\limits_{j = 1}^N {{a_{ij}}} [{x_j}(k - d) - {x_i}(k - d)],$ | (2) |
where ${{\rm{k}}_{\rm{1}}}$ is a fixed control gain and independent of the index $i$.
In case the network topology is exactly known,we design the following protocol to eliminate the effect of delay on consensus
| $\begin{array}{l} {u_i}(k) = \frac{{{k_1}}}{b}{a^d}\sum\limits_{j = 1}^N {{a_{ij}}} [{x_j}(k - d) - {x_i}(k - d)] + \\ {k_2}\sum\limits_{l = 1}^d {\sum\limits_{j = 1}^N {{a_{ij}}} } {a^{l - 1}}[{u_j}(k - l) - {u_i}(k - l)], \end{array}$ | (3) |
where ${k_1},{k_2}$ are fixed control gains and are independent of agent's index $i$.
Remark 1.It should be noted that the designing of protocol (3) adopts the predictor-like technique,which is inspired by the famous Smith predictor[19],the finite spectrum assignment method[20] and the Artstein reduction[21].
Remark 2. In the designing of protocol (3),we assume that the constant communication delay is exactly known. However,in case that the constant delay is unknown,we can get the delay information by the method of "time-stamping" in [22],i.e., all the transferred information is marked with the time when it was generated,then the time delay can be calculated by comparing the "time stamp" with the local clock.
Remark 3. In protocol (3),the distributed historical input information are used in the protocol design. In fact, comparing with the relative state information,agent's own state information cannot be used directly. However,it is feasible for agent to acquire its own historical input information. Thus,every agent can transmit its own historical input information to neighbors directly on the condition that the network topology is exactly known. It should be noted that similar protocol named as predictor feedback protocol has been given in [12]. Besides, literature [23] has also used the relative input information in the protocol design.
To further show the reasonability of the designed protocol (3),we give a physical example as follows.
Suppose there are $N$ aircrafts flying in the same direction with dynamics
\begin{align*} x_{i}(k+1)=x_{i}(k)+\Delta T u_{i}(k),i=1,2,\cdots,N, \end{align*}where $\Delta T>0$ is sampling time. It is known that formation keeping for aircrafts is an important issue in reality. As a special case,this example aims to guarantee that the distance between any two aircrafts is zero along the flying direction. Assume $x_{i}(k)$ is the position of the $i$-th aircraft,and $u_{i}(k)$ is the corresponding velocity controller[24]. In the flying direction,considering that the relative position detected by aircrafts are delayed by constant $d$,i.e., $\sum_{j=1}^{N}a_{ij}[x_{j}(k-d)-x_{i}(k-d)]$. To eliminate the effect of delay on the aim above,every pilot in the aircraft is required to send part of historical velocities to neighbors.
If the communication delay only affects the actually transmitted information as in [10] and [13],we design the following protocol
| ${u_i}(k) = \frac{{{k_1}}}{b}\sum\limits_{j = 1}^N {\frac{{{a_{ij}}}}{{{d_i}}}} [{x_j}(k - d) - {x_i}(k)]$, | (4) |
where $d \in {{\bf{Z}}^ + }$ is the communication delay,and ${d_i} = \sum\limits_{j = 1}^N {{a_{ij}}} $ is the degree of agent $i$.
Without loss of generality,we additionally set the initial values ${x_i}(\theta ) = 0$ and $u_{i}(\theta)=0$ for any $\theta<0$ to make the systems (1) operational under above given protocols. The definition of consensus is shown as follows.
Definition 1. Given an undirected graph $G$, the discrete-time multi-agent systems (1) are said to achieve consensus under the designed protocols above if for any finite initial values,the states of all agents satisfy $\|x_{j}(k)-x_{i}(k)\|\rightarrow 0$ as $k \to \infty $ for $i,j \in N.$
From above definition,it is obvious to know that the consensus problem can be solved when the systems (1) are stable by taking $u_{i}(k)\equiv 0$. In this paper,we focus on unstable multi-agent systems,i.e.,$|a|\geq 1$ in (1) to make the problem interesting. The problems studied in this paper are as follows
1) Provide conditions such that multi-agent systems (1) achieve consensus under protocols (3) and (4),respectively.
2) Comparing with the commonly used protocol (1),show the advantage of the designed protocol (3).
Remark 4. The problem studied in this paper is more general than those investigated in [7,13] and [17]. In fact,[7] concerns consensus without time delay; [13] is limited to time-invariant delay and [17] focuses on the systems that are at most critically unstable.
Ⅳ. MAIN RESULTSIn this section,only the case of $a\geq 1$ in (1) is considered, and the results for $a\leq -1$ can similarly be obtained. Before presenting our main results,we first show the following technical lemmas.
A. LemmasThe following lemma can be found in [25].
Lemma 1. Consider a retarded difference equation
$$\left\{ \begin{array}{l} x(k + 1) = f(x(k),{x_k}),{\mkern 1mu} {\mkern 1mu} x(k) \in {\bf{R}},\\ {x_0}(s) = \phi (s),{\mkern 1mu} {\mkern 1mu} \phi \in {C_r}, \end{array} \right.$$where $x_{k}(s)=x(k+s)$,and $s \in \{ - r, - r + 1, \ldots ,0\} $. The function $f$: ${\bf{R}} \times {C_r}$ is such that the image by $f$ of $\textbf{R}\times$(a bounded subset of ${C_r}$) is a bounded subset of R and the functions $u,v,w,p$: ${{\bf{R}}^ + } \to {{\bf{R}}^ + }$are continuous and strictly increasing functions,with $u(0)=v(0)=0$ and $p(t)>t$ for any $t>0$. Suppose that there is a continuous function $V:{\bf{R}} \to {\bf{R}}$,such that for all $x \in {\rm{R}}$ the following conditions are satisfied,
1) $u(\|x\|) \leq V(x) \leq v(\|x\|)$;
2) $\Delta V(x(k))=V(x(k+1))-V(x(k))\leq -\omega(\|x(k)\|)$,if $V(x(k +s)) < p V(x(k))),\forall \theta \in [-r,0]$;
3) $\lim_{s \rightarrow \infty}u(s)=\infty$.
Then the retarded difference equation is globally uniformly asymptotically stable.
Lemma 1,we can get the following lemma,which plays an important role in this section.
Lemma 2. For the discrete-time delayed system $\eta(k+1)=f\eta(k)+g\eta(k-d)$,where $f \in {\rm{ R}},g \in {\rm{R}}$ are constants,if $|f|+|g|<1$,the delayed system is asymptotically stable at $\eta(k)\equiv 0$.
Proof. If $g=0$,it is obvious that $\lim_{k \rightarrow \infty} \eta(k)=0$ from $|f|<1$. Without loss of generality,in the following we assume $g\neq 0$. Take a function $V(\eta(k))=|\eta(k)|$. Then
\begin{align*} &\Delta V(\eta(k))=V(\eta(k+1))-V(\eta(k))=\\ &\qquad |f\eta(k)+g\eta(k-d)|-|\eta(k)|\leq\\ &\qquad (|f|-1)V(\eta(k))+|g|V(\eta(k-d)). \end{align*}Let $p = \frac{{1 - |f| + |g|}}{{2|g|}}.$ Then it yields from $|f| + |g| < 1$ that $p > \frac{{2|g|}}{{2|g|}} = 1.$ If $fV(\eta (k - d)) < pV(\eta (k))$,it follows $\Delta V(\eta (k)) \le \frac{{|f| + |g| - 1}}{2}V(\eta (k))$. From $\frac{{|f| + |g| - 1}}{2} < 0$ and Lemma 1,the delayed system is asymptotically stable at $\eta (k) \equiv 0$.
Lemma 3[25]. For the scalar delayed system
\begin{align*} \left\{\begin{aligned} &x(k+1)=\beta x(k)+u(k-r),\,|\beta|>1,\\ &u(k)=-\alpha x(k),\,\alpha \in \textbf{R}, \end{aligned} \right. \end{align*}there exists constant $r^{*}>0$ such that the delayed system is not asymptotically stable for any choice of the feedback gain $\alpha$ if the delay $r \ge {r^ * }$.
B. Consensus ResultsNow,we are in position to give the main results of this paper. We first show the consensus result of multi-agent systems (1) with $a>1$ under protocol (3).
Theorem 1. Assume that the network topology is exactly known and $d$ is an any large yet bounded constant. Then the multi-agent systems (1) with $a>1$ achieve consensus under protocol (3) if $a < \frac{{{\lambda _N} + {\lambda _2}}}{{{\lambda _N} - {\lambda _2}}}$. Moreover,control gains satisfy $\frac{{a - 1}}{{{\lambda _2}}} < {k_1} < \frac{{a + 1}}{{{\lambda _N}}}$ and ${\beta _1} < {k_2} < \beta 2$,where
\begin{align*} \left\{\begin{aligned} &\beta_{1}\!=\!\max\{\!\frac{a^{d}k_{1}\lambda_{N}\!-\!1}{a^{d}\lambda_{N}}, \frac{a^{d}k_{1}\lambda_{N}\!-\!a\!-\!1}{(a^{d}\!-\!1)\lambda_{N}}, \frac{a^{d}k_{1}\lambda_{2}\!+\!a\!-\!1}{(a^{d}\!+\!1)\lambda_{2}}\},\\ &\beta_{2}\!=\!\min\{\!\frac{a^{d}k_{1}\lambda_{N}\!+\!1}{a^{d}\lambda_{N}}, \frac{a^{d}k_{1}\lambda_{N}\!+\!a\!+\!1}{(a^{d}\!+\!1)\lambda_{N}}, \frac{a^{d}k_{1}\lambda_{2}\!-\!a\!+\!1}{(a^{d}\!-\!1)\lambda_{2}}\}. \end{aligned} \right. \end{align*}Proof. Inserting protocol (3) into systems (1) follows
\begin{align*} &x_{i}(k+1)=ax_{i}(k)\!+\!k_{1}a^{d}\sum_{j=1}^{N}a_{ij}[x_{j}(k-d)\!-\!x_{i}(k-d)]+\\ &\qquad k_{2}\sum_{j=1}^{N}a_{ij}\sum_{l=1}^{d}a^{l-1}b[u_{j}(k-l)\!-\!u_{i}(k-l)]. \end{align*}From systems (1),it yields $bu_{i}(k-l)=x_{i}(k+1-l)-ax_{i}(k-l)$,thus $\sum_{l=1}^{d}a^{l-1}bu_{i}(k-l)=x_{i}(k)-a^{d}x_{i}(k-d)$. Then
| $\begin{array}{l} {x_i}(k + 1) = a{x_i}(k) + {k_2}\sum\limits_{j = 1}^N {{a_{ij}}} [{x_j}(k) - {x_i}(k)] + \\ {a^d}({k_1} - {k_2})\sum\limits_{j = 1}^N {{a_{ij}}} [{x_j}(k - d) - {x_i}(k - d)]. \end{array}$ | (5) |
Let $x(k): = {[{x_1}(k), \cdots ,{x_N}(k)]^{\rm{T}}}$. Based on (5), the dynamical equation of $x(k)$ can be written as
| $x(k + 1) = [a{I_N} - {k_2}{L_G}]x(k) - {a^d}[{k_1} - {k_2}]{L_G}x(k - d).$ | (6) |
Denote the average state of all the agents at time $k$ by $\overline{x}(k):= \frac{1}{N}\sum^{N}_{i=1}x_{i}(k)=\frac{1}{N}\mathbf{1}_{N}^{\rm T}x(k)$. Note $\mathbf{1}_{N}^{\rm T}L_{\mathcal{G}}=0$,thus $\overline{x}(k+1)=a\overline{x}(k)$ from (6). Represent the deviation of each agent from the average state by $\delta_{i}(k):= x_{i}(k) -\overline{x}(k)$,and $\delta (k): = {[{\delta _1}(k), \cdots ,{\delta _N}(k)]^{\rm{T}}}$. Then
| $\delta (k + 1) = [a{{\bf{I}}_N} - {k_2}{L_G}]\delta (k) - {a^d}[{k_1} - {k_2}]{L_G}\delta (k - d)$ | (7) |
Considering $\parallel {x_i}(k) - \bar x(k)\parallel = \frac{1}{N}\parallel \sum _{j = 1}^N{\rm{[}}{x_j}(k) - {x_i}(k)]\parallel \le \frac{1}{N}\sum _{j = 1}^N\parallel {x_j}(k) - {x_i}(k)\parallel $,and $\parallel {x_j}(k) - {x_i}(k)\parallel \le \parallel {x_j}(k) - \bar x(k)\parallel + \parallel {x_i}(k) - \bar x(k)\parallel $,we know the consensus problem is equivalent to the stability of the error system (7).
Select vector ${\phi _i} \in {{\bf{R}}^N}$ such that $\phi _i^{\rm{T}}{L_G} = {\lambda _i}\phi _i^{\rm{T}}$, and form a unitary matrix $\Phi = [\frac{{{{\bf{1}}_N}}}{{\sqrt N }},{\phi _2}, \cdots ,{\phi _N}]$to transform ${L_G}$ into a diagonal form ${\Phi ^{\rm{T}}}{L_G}\Phi = {\rm{diag}}\{ 0,{\lambda _2}, \cdots ,{\lambda _N}\} $. Denote $\widetilde{\delta}(k)\triangleq {\it {\varPhi}^{\rm T}}{\delta}(k)$ and partition $\tilde \delta (k) \in {{\bf{R}}^N}$ into $N$ parts,i.e.,$\delta (k) = {[{\delta _1}(k), \ldots ,{\delta _N}(k)]^{\rm{T}}}$. Then $\widetilde{\delta}_{1}(k)=\frac{1}{\sqrt{N}}\sum^{N}_{i=1}\delta_{i}(k)\equiv 0$. Consider matrix $\Phi $ is nonsingular,it follows from (7) that the consensus problem is equivalent to the stability of systems
| ${\tilde \delta _i}(k + 1) = [a - {k_2}{\lambda _i}]{\tilde \delta _i}(k) - {a^d}[{k_1} - {k_2}]{\lambda _i}{\tilde \delta _i}(k - d),$ | (8) |
where $i \in \{ 2, \cdots ,N\} $. From $a>1$ and the condition $a < \frac{{{\lambda _N} + {\lambda _2}}}{{{\lambda _N} - {\lambda _2}}}$,we know ${\lambda _i} > 0$ for $i \in \{ 2, \cdots ,N\} $. In the following,we aim to prove that ${\lim _{k \to \infty }}{\tilde \delta _i}(k) = 0$ for $i \in \{ 2, \cdots ,N{\rm{\} }}$ under the condition in the theorem.
From Lemma 2 and (8),the consensus is achieved if $|a-k_{2}\lambda_{i}|+a^{d}|k_{1}-k_{2}|\lambda_{i}<1$,which is
| $\left\{ \begin{array}{l} {a^d}|{k_1} - {k_2}|{\lambda _i} < 1,\\ |a - {k_2}{\lambda _i}| < 1 - {a^d}|{k_1} - {k_2}|{\lambda _i}, \end{array} \right.$ | (9) |
for $i \in \{ 2, \cdots ,N\} $.
It yields from condition $a < \frac{{{\lambda _N} + {\lambda _2}}}{{{\lambda _N} - {\lambda _2}}}$ that there exists constant ${k_1}$ satisfying $\frac{{a - 1}}{{{\lambda _2}}} < {k_1} < \frac{{a + 1}}{{{\lambda _N}}}$. After simple computation,we know that $\frac{{a - 1}}{{{\lambda _2}}} < \forall {k_1} < \frac{{a + 1}}{{{\lambda _N}}}$ leads to ${\beta _1} < {k_1} < {\beta _2}$. We divide the proof into the following three cases.
1) $\frac{{a - 1}}{{{\lambda _2}}} < {k_1} < \frac{{a + 1}}{{{\lambda _N}}}$ and ${\beta _1} < {k_2} < {k_1}.$ Obviously,${k_1} - {k_2} > 0$ can be obtained. Then,condition ${k_2} > {\beta _1} \ge \frac{{{a^d}{k_1}{\lambda _N} - 1}}{{{a^d}{\lambda _N}}}$ leads to
\begin{align} 0 < |{k_1} - {k_2}| = {k_1} - {k_2} < {k_1} - \frac{{{a^d}{k_1}{\lambda _N} - 1}}{{{a^d}{\lambda _N}}} = \frac{1}{{{a^d}{\lambda _N}}}. \end{align}Thus $0 < {a^d}|{k_2} - {k_1}|{\lambda _N} < 1$,which means that the first inequality of (9) holds for $i \in \{ 2, \cdots ,N\} $. On the other hand,the second inequality of (9) becomes
| $|a - {k_2}{\lambda _i}| < 1 - {a^d}({k_1} - {k_2}){\lambda _i}.$ | (10) |
The solution of above inequality is
\begin{align*} k_{2}>\max\{\frac{a^{d}k_{1}\lambda_{i}-a-1}{(a^{d}-1)\lambda_{i}}, \frac{a^{d}k_{1}\lambda_{i}+a-1}{(a^{d}+1)\lambda_{i}}\}. \end{align*}From ${k_2} > {\beta _1}$,it is easy to know inequality (10) holds simultaneously for $i \in \{ 2, \cdots ,N\} $. Thus the consensus is achieved.
2) $\frac{{a - 1}}{{{\lambda _2}}} < {k_1} < \frac{{a + 1}}{{{\lambda _N}}}$ and ${k_2} = {k_1}$. In this case,${a^d}|{k_2} - {k_1}|{\lambda _i} = 0 < 1$, thus the first inequality of (9) holds for $i \in \{ 2, \cdots ,N\} $. On the other hand,the second inequality of (9) becomes $|a - {k_2}{\lambda _i}| < 1$,which is $\frac{{a - 1}}{{{\lambda _i}}} < {k_2} < \frac{{a + 1}}{{{\lambda _i}}}$,and this inequality holds simultaneously for $i \in \{ 2, \cdots ,N\} $ if and only if $\frac{{a - 1}}{{{\lambda _2}}} < {k_2} < \frac{{a + 1}}{{{\lambda _N}}}$. Thus,the consensus is reached in this case.
3) $\frac{{a - 1}}{{{\lambda _2}}} < {k_1} < \frac{{a + 1}}{{{\lambda _N}}}$ and ${k_1} < {k_2} < {\beta _2}$. In this case,it is easy to obtain ${k_1} - {k_2} < 0$. Condition ${k_2} < {\beta _2} \le \frac{{{a^d}{k_1}{\lambda _N} + 1}}{{{a^d}{\lambda _N}}}$ yields
\begin{align*} k_{1}-k_{2}>k_{1}-\frac{a^{d}k_{1}\lambda_{N}+1}{a^{d}\lambda_N}=-\frac{1}{a^{d}\lambda_{N}}. \end{align*}Thus,$0 < {a^d}|{k_2} - {k_1}|{\lambda _N} < 1$. Similarly as proven in 1),consensus can be guaranteed.
Remark 5. It is shown in Theorem 1 that the consensus condition is related to $\frac{{{\lambda _2}}}{{{\lambda _N}}}$,i.e., the eigenratio of undirected graph $G$. Thus,the more unstable are the multi-agent systems,the bigger eigenratio corresponding a topology with better synchronizability is needed to guarantee consensus. Especially,when the undirected $G$ is completed,any unstable agent dynamics is allowed for consensus by the method in Theorem 1.
When $a=1$,the above method is also applicable,and we give the following corollary.
Corollary 1. Consider the multi-agent systems (1) with $a=1$,then the consensus is achieved under protocol (3) with any large yet bounded delay if the undirected graph $\mathbf{\mathcal{G}}$ is connected. Moreover, the control gains are selected as $0 < {k_1} < \frac{2}{{{\lambda _N}}}$ and $\frac{{{k_1}}}{2} < {k_2} < \frac{{{k_1}}}{2} + \frac{1}{{{\lambda _N}}}$.
Proof. The proof is similar to Theorem 1 and omitted for simplicity.
To show the advantage of protocol (3),we investigate the consensus problem of multi-agent systems (1) with $a>1$ under the commonly used protocol (2).
Theorem 2. For any connected undirected graph $\mathcal{G}$, the multi-agent systems (1) cannot achieve consensus under protocol (2) for any gain $k_{1} \in \textbf{R}$ if the communication delay is large enough.
Proof. From protocol (2) and systems (1),we get
\begin{align*} x_{i}(k+1)=ax_{i}(k)+k_{1}\sum_{j=1}^{N}a_{ij}[x_{j}(k-d)-x_{i}(k-d)]. \end{align*}By the method in Theorem 1,it yields that the consensus is achieved if and only if the error system
\begin{align*} \tilde{\delta}_{i}(k+1)=a\tilde{\delta}_{i}(k) -k_{1}\lambda_{i}\tilde{\delta}_{i}(k-d) \end{align*}is stable simultaneously for $i \in \{2, \cdots, N\}$. Due to $a>1$ and in view of Lemma 3,the proof is completed.
Remark 6. It is known from Theorem 2 that the communication delay indeed affects consensus. However,the results in Theorem 1 show that the effect of delay on consensus can be eliminated if the network topology is exactly known and every agent transmits historical input information to neighbors.
In the following,we are to state the consensus result of the discrete-time multi-agent systems (1) under protocol (4).
When the undirected graph $\mathcal{G}$ is connected, we know that matrix $[\mathcal{D}^{-1}\mathcal{A}]$ is an $N \times N$ irreducible stochastic matrix[26],and there is a unique invariant probability vector${\alpha}=[\alpha_{1}, \alpha_{2}, \cdots, \alpha_{N}]^{\rm T}$ with $\alpha_{i}>0$, $\forall i \in \mathcal{N}$ and $\sum^{N}_{j=1}\alpha_{i}=1$ such that ${\alpha}^{\rm T}[\mathcal{D}^{-1}\mathcal{A}]={\alpha}^{\rm T}$. In the following,let $\mu_{i}, i \in \mathcal{N}$ denote the eigenvalues of matrix $[\mathcal{D}^{-1}\mathcal{A}]$. It is known from Lemma 1 in [27] that matrix $[\mathcal{D}^{-1}\mathcal{A}]$ has a simple eigenvalue $\mu_{1}=1$ if the undirected graph $\mathcal{G}$ is connected,and other eigenvalues are real with modulus no bigger than 1. Without loss generality,let $\mu_{N}=\max\{|\mu_{i}|, i=2, \cdots, N\}$. Now,we state the following result.
Theorem 3. Assume the undirected graph $\mathcal{G}$ is connected. Then the consensus of the multi-agent systems (1) is achieved under protocol (4) with any large yet bounded delay if the agent dynamics and the network topology satisfy $1 \leq a <\frac{1}{|\mu_{N}|}$. Moreover, the control gain is selected as $\frac{{a - 1}}{{1 - |{\mu _N}|}} < {k_1} < \frac{{a + 1}}{{1 + |{\mu _N}|}}$.
Proof. Inserting protocol (4) into systems (1) gives
\begin{align*} x_{i}(k+1)=ax_{i}(k)-k_{1}x_{i}(k)+k_{1}\sum^{N}_{j=1}\frac{a_{ij}}{d_{i}}x_{j}(k-d). \end{align*}Then,it is easy to get
| \begin{align} {X}(k+1)=[a-k_{1}]{X}(k)+k_{1}[\mathcal{D}^{-1}\mathcal{A}]{X}(k-d), \end{align} | (11) |
where ${X}(k)=[x_{1}(k), x_{2}(k), \cdots, x_{N}(k)]^{\rm T}$.
Due to matrix $[\mathcal{D}^{-1}\mathcal{A}]$ may not be symmetric,we use $\overline{X}(k):={\alpha}^{\rm T}{X}(k)$ to denote the weighted average state of all agents,then
\begin{align*} \overline{X}(k+1)=[a-k_{1}]\overline{X}(k)+k_{1}\overline{X}(k-d). \end{align*}Note that $[\mathcal{D}^{-1}L_{\mathcal{G}}]\mathbf{1}_{N}=0$ and $[\mathcal{D}^{-1}\mathcal{A}]={\textbf{I}}_{N}-[\mathcal{D}^{-1}L_{\mathcal{G}}]$, it follows
| \begin{align} \mathbf{1}_{N}\overline{X}(k+1)=[a-k_{1}]\mathbf{1}_{N}\overline{X}(k) +k_{1}[\mathcal{D}^{-1}\mathcal{A}]\mathbf{1}_{N}\overline{X}(k-d).\label{t3} \end{align} | (12) |
From (11) and (12),we get
\begin{align*} \delta(k+1)=[a-k_{1}]\delta(k)+k_{1}[\mathcal{D}^{-1}\mathcal{A}]\delta(k-d), \end{align*}where $\delta(k)=X(k)-\mathbf{1}_{N}\overline{X}(k)$. Then, according to the proof in Theorem 1,the consensus problem is equivalent to the simultaneous stability of error systems
\begin{align*} \tilde{\delta}_{i}(k+1)=[a-k_{1}]\tilde{\delta}_{i}(k) +k_{1}\mu_{i}\tilde{\delta}_{i}(k-d),\,i \in\{2,\cdots,N\}, \end{align*}where $\tilde{\delta}_{1}(k)=\sum^{N}_{i=1}\alpha_{i}x_{i}(k)-\overline{X}(k)\equiv0$. From Lemma 2,we only need to find gain $k_{1}$ such that inequality
| \begin{align} |a-k_{1}|+|k_{1}\mu_{i}|<1 , \end{align} | (13) |
holds simultaneously for $i\in \{2, \cdots, N\}$.
If $\mu_{i}\neq 0$,the solution of inequalities (13) is $0 < {k_1} < \frac{1}{{|{\mu _i}|}}$ and $\frac{{a - 1}}{{1 - |{\mu _i}|}} < {k_1} < \frac{{a + 1}}{{|{\mu _i}| + 1}}.$ It is easy to know that the condition $1\leq a <\frac{1}{|\mu_{N}|}$ in the theorem ensures the existence of $k_{1}$ such that $\frac{{a - 1}}{{1 - |{\mu _N}|}} < {k_1} < \min \{ \frac{{a + 1}}{{1 + |{\mu _N}|}},\frac{1}{{|{\mu _N}|}}\} = \frac{{a + 1}}{{1 + |{\mu _N}|}}$, it is easy to guarantee inequality (13) from the selection of $k_{1}$ in the theorem. Thus, inequalities (13) hold simultaneously for $i \in \{2, \cdots, N\}$ under the condition in the theorem and the consensus is achieved.
Remark 7. The condition for consensus becomes $1 \le a < N$ if the network topology in Theorem 3 is complete,where $N$ is the number of the agents in the network. In fact,when the undirected graph $\mathcal{G}$ in Theorem 3 is complete, the eigenvalues of matrix $[\mathcal{D}^{-1}\mathcal{A}]$ satisfy $\mu_{1}=1$ and $\mu_{2}=\cdots=\mu_{N}=\frac{1}{N}$.
Remark 8. It should be noted that the communication delay in protocol (4) is allowed to be unknown. In fact,from the proof of Theorem 3,the precise information of the delay or the historical input information of agents is not needed. In addition, Lemma 1 and the proof of Theorem 3 admit the communication delay to be time-varying in protocol (4) by using exactly the same method in Theorem 3.
Ⅴ. SIMULATIONSIn this section,two examples are carried out to verify the theoretical results obtained by the previous analysis.
Consider a network consisting of 4 agents indexed by 1,2,3,4, respectively. The topology among those agents is described by an undirected graph $\mathcal{G}=\{\mathcal{V}, \mathcal{E}, \mathcal{A}\}$, where $\mathcal{V}=\{1, 2, 3, 4\}$. The adjacency matrix and Laplacian matrix are described as
\begin{align*} \mathcal{A}=\left[ \begin{array}{cccc} 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ \end{array} \right]\, \mbox{and}\, L_{\mathcal{G}}=\left[ \begin{array}{cccc} 3 & -1 & -1 & -1 \\ -1 & 2 & 0 & -1 \\ -1 & 0 & 2 & -1 \\ -1 & -1 & -1 & 3 \\ \end{array} \right]. \end{align*}Clearly,undirected graph $\mathcal{G}$ is connected and the nonzero eigenvalues of $L_{\mathcal{G}}$ are $\lambda_{2}=2,\lambda_{3}=4$ and $\lambda_{4}=4$. Under the connected undirected graph $\mathcal{G}$, we consider the following two examples.
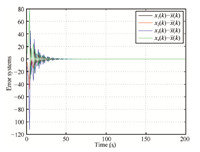
Example 1. Assume $a=2,b=2$ in the discrete-time agent dynamics (1). Let the initial values be given as $x(0)=[8,2,-4,8]^{\rm T}$ and $x_{i}(s)=0, u_{i}(s)=0$ for any $s<0$. Given the communication delay $d=4$, make use of protocol (3) and take gains $k_{1}=0.6$ and $k_{2}=0.606$ in view of Theorem 1, then Fig. 1 shows the asymptotic stability of the error systems, where $\overline{x}(k)=\frac{1}{4}[x_{1}(k)+x_{2}(k)+x_{3}(k)+x_{4}(k)]$.
|
Download:
|
| Fig. 1. Example 1. | |
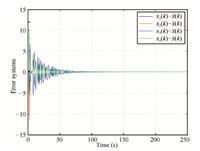
Example 2. With simple computation,the eigenvalues of matrix $[\mathcal{D}^{-1}\mathcal{A}]$ are $\mu_{1}=1, \mu_{2}=0, \mu_{3}=-\frac{1}{3}$ and $\mu_{4}=-\frac{2}{3}$. From Theorem 3, the allowable range of the system gain is $1\leq a<\frac{3}{2}$. Take parameters $a=1.4, b=1$ and design the protocol as
\begin{align*} u_{i}(k)=k_{1}\sum^{4}_{j=1}\frac{a_{ij}}{d_{i}}[x_{j}(k-\lfloor 4{\rm sin}^{2}(k)\rfloor)-x_{i}(k)] \end{align*}where $\lfloor4{\rm sin}^{2}(k)\rfloor$ represents to the integer part of time-varying communication delay $4{\rm sin}^{2}(k)$. From Theorem 3,take consensus gain $k_{1}=1.31$,then for the given initial values $x(0)=[10,-2,5,20]^{\rm T}$ and $x_{i}(s)=0\,(s<0)$, Fig. 2 reveals the error systems converge to zero asymptotically, where $\overline{X}(k)=0.3x_{1}(k)+0.2x_{2}(k)+0.2x_{3}(k)+0.3x_{4}(k)$ denotes the weighted average state of all agents.
|
Download:
|
| Fig. 2. Example 2. | |
This paper addresses the consensus problem for unstable discrete-time multi-agent systems with two kinds of communication delays,which only affect the relative information and the actually transmitted information,respectively. The effect of the first kind of communication delay is eliminated if the network topology is exactly known. Sufficient condition for consensus is provided in case of the second communication delay,where the delay is also allowed to be unknown and time-varying in this case. It is worth mentioning that the proposed results are expected to extend to the vector state and the time-varying topology.
| [1] | Pettersen K, Gravdahl J T, Nijmeijer H. Group Coordination and Cooperative Control. Berlin:Springer, 2006. |
| [2] | Cao Y C, Ren W, Meng Z Y. Decentralized finite-time sliding mode estimators and their applications in decentralized finite-time formation tracking. System & Control Letters, 2010, 59(9):522-529 |
| [3] | Yu W W, Chen G R, Cao M. Distributed Leader-follower flocking control for multi-agent dynamical systems with time-varying velocities. System & Control Letters, 2010, 59(9):543-552 |
| [4] | Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O. Novel type of phase transition in a system of self-driven particles. Physical Review Letters, 1995, 75(6):1226-1229 |
| [5] | Jadbabaie A, Lin J, Morse A S. Coordination of groups of mobile automous agents using nearest neighbor rules. IEEE Transactions on Automatic Control, 2003, 48(6):998-1001 |
| [6] | Hong Y G, Wang X L. Multi-agent tracking of a high-dimensional active leader with switching topology. Journal of Systems Science and Complexity, 2009, 22(4):722-731 |
| [7] | You K Y, Xie L H. Network topology and communication data rate for consensusability of discrete-time multi-agent systems. IEEE Transactions on Automatic Control, 2011, 56(10):2062-2075 |
| [8] | Tian Y P, Liu C L. Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations. Automatica, 2009, 45(5):1347-1353 |
| [9] | Olfati-Saber R, Murray R M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Transactions on Automatic Control, 2004, 49(9):1520-1533 |
| [10] | Moreau L. Stability of continuous-time distributed consensus algorithms. In:Proceedings of the 43rd IEEE Conference on Decision and Control. Nassau:IEEE, 2004. 3998-4003 |
| [11] | Yu W W, Chen G R, Cao M, Ren W. Delay-induced consensus and quasi-consensus in multi-agent dynamical systems. IEEE Transactions on Circuits and Systems, Part I:Regular Paper, 2013, 60(10):2679-2687 |
| [12] | Zhou B, Lin Z L. Consensus of high-order multi-agent systems with large input and communication delays. Automatica, 2014, 50(2):452-464 |
| [13] | Tian Y P, Liu C L. Consensus of multi-agent systems with diverse input and communication delays. IEEE Transactions on Automatic Control, 2008, 53(9):2122-2128 |
| [14] | Xu J J, Zhang H S, Xie L H. Input delay marigin for consensusability of multi-agent systems. Automatica, 2013, 49(6):1816-1820 |
| [15] | Tan C, Liu G P. Consensus of discrete-time linear networked multi-agent systems with communication delays. IEEE Transactions on Automatic Control, 2013, 58(11):2962-2968 |
| [16] | Lin P, Ren W. Constrained consensus in unbalanced networks with communication delays. IEEE Transactions on Automatic Control, 2014, 59(3):775-781 |
| [17] | Wang X, Saberi A, Stoovogel A A, Grip H F, Yang T. Synchronization in a network of identical discrete-time agents with uniform constant communication delay. International Journal of Robust and Nonlinear Control, 2013, 24(18):3076-3091 |
| [18] | Barahona M, Pecora L M. Synchronization in small-word systems. Physical Review Letters, 2002, 89(5):054101 |
| [19] | Smith O. Controller to overcome dead time. Instrument Society of America-Journal, 1959, 6(2):28-33 |
| [20] | Manitius A, Olbrot A. Finite spectrum assignment problem for systems with delays. IEEE Transactions on Automatic Control, 1979, 24(4):541-553 |
| [21] | Artstein Z. Linear systems with delayed control:a reduction. IEEE Transactions on Automatic Control, 1982, 27(4):869-879 |
| [22] | Hua J W, Liang T, Sun H X, Lei Z M. Time-delay compensation control of networked control systems using time-stemp based state prediction. In:Proceedings of the 2008 ISECS International Colloquium on Computing, Communication, Control, and Management. Washington, DC, USA:IEEE, 2008. 198-202 |
| [23] | You K Y, Xie L H. Coordination of discrete-time multi-agent systems via relative output feedback. International Journal of Robust and Nonlinear Control, 2011, 21(13):1587-1605 |
| [24] | Ren W, Atkins E. Distributed multi-vehicle coordinated control via local information exchange. International Journal of Robust and Nonlinear Control, 2007, 17(10-11):1002-1033 |
| [25] | Lin Z L. On asymptotic stabilizability of discrete-time linear systems with delayed input. Communications in Information and Systems, 2007, 7(3):227-264 |
| [26] | Fang H T, Chen H F, Wen L. On control of strong consensus for networked agents with noisy observations. Journal of Systems Science and Complexity, 2012, 25(1):1-12 |
| [27] | Zeng L, Hu G D. Consensus of linear multi-agent systems with communication and input delays. Acta Automatica Sinica, 2013, 39(7):1133-1140 |
 2015, Vol.2
2015, Vol.2 


