HYPERSONIC vehicles are aircrafts with a speed of Mach 5 or higher. The two typical hypersonic vehicles are the air-breathing cruise vehicle[1, 2] and the un-powered gliding reentry vehicle[3]. The latter can remotely maneuver in the near space (from about 100km to 20km in altitude[4]) without any power. Since the flight environment of the near space is terrible,an advanced guidance,navigation and control (GNC) system has become one of the key technologies for the reentry flight[5].
The reentry guidance method based on a reference trajectory is a common approach that has been successfully used in the Shuttle[6, 7]. The basic idea of this approach is tracking a pre-designed reference trajectory onboard during the reentry flight. However,the tracking law design is usually complex mainly due to the following reasons:
1) Strong nonlinear terms exist in the reentry dynamic model;
2) Parameters in the aerodynamic model are with high uncertainty;
3) The number of state variables (altitude,range-to-go,velocity,heading angle,etc.) is greater than that of control variables (only the angle of attack and the bank angle).
To solve this tracking problem,[8] proposed an approximate receding-horizon control law based on the linearized time-varying model with six state variables. Under this control law,the three-dimensional trajectory can be tracked well when the flight initial condition is dispersed. But for large aerodynamic dispersions,it is sometimes hard for this law to own a good performance. In [9],the longitudinal trajectory consisting of three state variables was analyzed and a tracking law based on the linear quadratic regulator (LQR) was developed. Though the guidance algorithm in this approach is much more simplified,its anti-interference ability is not always perfect as the feedback matrix is designed off-line. To improve the performance of trajectory tracking,[10] investigated an adaptive control method,[11] used a prediction control approach,[12] introduced the predictive controller into the drag tracking,[13] studied a tracking law based on the inversion control,[14] proposed an adaptive optimal sliding mode controller,and [15] presented a flatness approach. However,most of these approaches are designed based on the multiple-input multiple-output (MIMO) system where couplings exist among control channels,and significantly complex algorithm is required to overcome the couplings.
In fact,to ensure the reliability of the control and guidance system,the trajectory tracking law should be designed under the following two principles:
1) The tracking law is robust to any dispersion;
2) The algorithm is simple to be employed.
In this paper,a decoupling approach is proposed for the design of the trajectory tracking law. Different from those complex approaches mainly focusing on the first principle,this study pays attention to both principles.
In the longitudinal plane,to simplify the tracking algorithm,the MIMO system for the multi-objective tracking is separated into a series of two single-input single-output (SISO) subsystems. The former is for velocity tracking,and the latter is for altitude tracking. In each subsystem,to overcome the model uncertainty,sliding mode control (SMC) is used in the tracking law. Finally,simulations on a gliding reentry vehicle model are carried out to validate the proposed approach.
II. REENTRY GUIDANCE PROBLEM A. Reentry DynamicsThe three-degree-of-freedom (3 DOF) point-mass equations of an un-powered reentry vehicle over a spherical rotating Earth are as follows[16, 17]:
| $\begin{equation}\label{eq-r} \dot{r}=v \sin\gamma, \end{equation}$ | (1) |
| $\begin{equation}\label{eq-theta} \dot{\theta}=\frac{v \cos\gamma \sin\psi}{r\cos\phi}, \end{equation}$ | (2) |
| $\begin{equation}\label{eq-phi} \dot{\phi}=\frac{v \cos\gamma \cos\psi}{r}, \end{equation}$ | (3) |
| $\begin{array}{*{20}{l}} {\dot v = }&{ - D - g\sin \gamma + {\omega ^2}r\cos \phi (\sin \gamma \cos \phi - }\\ {}&{\cos \gamma \sin \phi \cos \psi ),} \end{array}$ | (4) |
| $\begin{align}\label{eq-gamma} \dot{\gamma}= & \frac{1}{v}[L\cos\sigma-g\cos\gamma+\frac{v^{2}\cos\gamma}{r}+2\omega v\cos\phi\sin\psi+\nonumber\\ & \omega^{2} r \cos\phi(\cos\gamma\cos\phi+\sin\gamma\sin\phi\cos\psi), \end{align}$ | (5) |
| $\begin{align}\label{eq-psi} \dot{\psi}= & \frac{1}{v}\Big[\frac{v^{2}\cos\gamma\sin\psi\tan\phi}{r}+ \frac{\omega^{2} r\sin\phi\cos\phi\sin\psi}{\cos\gamma}-\nonumber\\ & 2\omega v(\tan\gamma\cos\phi\cos\psi-\sin\phi)+\frac{L\sin\sigma}{\cos\gamma}\Big]. \end{align}$ | (6) |
Here,${r}$ is the radial distance from the center of the Earth to the vehicle. $\theta$ and $\phi$ are longitude and latitude,respectively. $v$ is the Earth-relative velocity. $\gamma$ and $\psi$ are the flight path angle and the velocity heading angle,respectively. $\sigma$ is the bank angle. $g$ is the gravitational acceleration,and $\omega$ is the angular rate of Earth rotation. $L$ and $D$ are the aerodynamic lift and drag accelerations,i.e.,
| $\left\{ \begin{array}{l} L = \frac{1}{{2m}}\rho {v^2}{C_L}(\alpha ){S_A},\\ D = \frac{1}{{2m}}\rho {v^2}{C_D}(\alpha ){S_A}, \end{array} \right.$ | (7) |
where $m$ is the mass of the vehicle,$S_A$ is the reference area,$C_{L}$ and $C_{D}$ are the lift and drag coefficients that depend on the angle of attack $\alpha$,and $\rho$ is the atmospheric density calculated by
| $\begin{equation}\label{eq-rho} \rho = \rho_{0}{\rm e}^{-\beta h}, \end{equation}$ | (8) |
where $\rho_{0}$ is the atmospheric density on the surface of the Earth,and $\beta$ is a constant. $h$ is the altitude and has the relationship with $r$ as in (9),where $R_{0}$ is the radius of the Earth.
| $\begin{equation}\label{eq-h} h = r-R_{0}. \end{equation}$ | (9) |
The guidance system$'$s mission is to provide commands with which the vehicle can travel from the initial interface to the terminal interface and the flight constraints are well satisfied. To simplify this system,we can design it separately in the longitudinal and lateral planes.
In the lateral plane,the control variable is the sign of the bank angle. With a conventional heading error corridor,the bank reversal logic is designed as
| $\begin{equation}\label{eq-reversal} \text{sgn}(\sigma)= \begin{cases} 1,& \text {if $\Delta\psi\geq\Delta\psi_{d}$},\\ \text{sgn}(\sigma_{k-1}),& \text {if $|\Delta\psi|<\Delta\psi_{d}$},\\ -1,& \text {if $\Delta\psi\leq-\Delta\psi_{d}$}, \end{cases} \end{equation}$ | (10) |
where $\sigma_{k-1}$ is the bank angle command in the previous guidance cycle,$\Delta\psi$ is the heading error and $\Delta\psi_{d}$ is the boundary of the heading error corridor.
In the longitudinal plane,the control variables include the magnitude of the bank angle and the angle of attack. The task for longitudinal guidance is tracking the reference trajectory with the flight constraints satisfied. The three typical reentry constraints are expressed as follows[17, 18]:
| $\begin{equation}\label{eq-constraints} \left\{ \begin{aligned} \dot{Q} & = K_{\dot{Q}}\rho^{0.5}v^{3.15}\leq \dot{Q}_{\max},\\ n & = L \cos\alpha+D\sin\alpha\leq n_{\max},\\ q & = \frac{1}{2}\rho v^{2}\leq q_{\max}, \end{aligned}\right. \end{equation}$ | (11) |
where $\dot{Q}$ is the heating rate,$n$ the normal aerodynamic load,$q$ the dynamic pressure,and $K_{\dot{Q}}$ is a constant.
Generally,a reference longitudinal trajectory is planned by the off-line optimization to satisfy reentry constraints,and then a reliable tracking law is employed onboard to track this reference trajectory.
III. DECOUPLING TRAJECTORY TRACKING A. Decoupling Design for Guidance SystemThe main state variables in the longitudinal plane are altitude,velocity,flight path angle and range-to-go $s_{\text{togo}}$. As the flight path angle can be controlled by the stable tracking of altitude,the task for control can be simplified to tracking the altitude and velocity trajectories with $s_{\text{togo}}$ as the independent variable.
Considering that $\omega^{2}\approx 0$ and $\gamma\approx 0$ in (4),the derivative of velocity is controlled directly by the aerodynamic drag $D$. Similarly,from (1) and (5),the derivative of altitude (which equals to the rate of $r$) is found to be controlled by $L\cos\sigma$. Furthermore,$L$ and $D$ in (7) mainly depend on $\rho$,$v$ and $\alpha$. Therefore,the function relations among control variables (the bank angle and the angle of attack) and state variables (altitude and velocity) are obtained as in Fig.1.
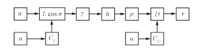
|
Download:
|
| Fig. 1. Function relations for controlvariables. | |
From Fig.1,it is found that the angle of attack has a direct effect on velocity,but the bank angle affects the velocity indirectly through flight path angle,altitude and the atmospheric density. After neglecting effects of the bank angle on velocity,the simplified relations are given by Fig.2. The velocity and the altitude are controlled by the angle of attack and bank angle,respectively,since the function from the angle of attack to the altitude can be supposed as dispersion in the lift model.
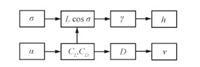
|
Download:
|
| Fig. 2. Simplified function relations for control variables. | |
Hence,the MIMO system for longitudinal trajectory control can be separated into two SISO subsystems: the velocity control and the altitude control. Considering that the angle of attack has an effect on altitude,a series connection for the two controllers is employed. The control diagram is designed as in Fig.3.
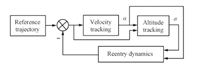
|
Download:
|
| Fig. 3. Diagram for decoupling tracking approach. | |
In Fig.3,the reference trajectory is given by the off-line optimization and saved as several discrete sequences,i.e.,$[v_{0},v_{1},v_{2},\cdots ,v_{n}]$,$[h_{0},h_{1},h_{2},\cdots ,h_{n}]$,and $[s_{\text{togo},0},s_{\text{togo},1},s_{\text{togo},2},\cdots ,s_{\text{togo},n}]$. Given $s_{\text{togo}}\in[s_{\text{togo},i+1},s_{\text{togo},i}]$,the reference velocity and altitude are calculated by (12) and (13). The first or second derivatives for $v_{\text{ref}}$ and $h_{\text{ref}}$ used in the trajectory tracking law can be calculated by the numerical differentiation,since the optimized reference trajectory is usually smooth.
| $\begin{equation}\label{eq-vref} v_{\text{ref}}(s_{\text{togo}})=v_{i}+\frac{v_{i+1}-v_{i}}{s_{\text{togo},i+1}-s_{\text{togo},i}}(s_{\text{togo}}-s_{\text{togo},i}) \end{equation}$ | (12) |
| $\begin{equation}\label{eq-href} h_{\text{ref}}(s_{\text{togo}})=h_{i}+\frac{h_{i+1}-h_{i}}{s_{\text{togo},i+1}-s_{\text{togo},i}}(s_{\text{togo}}-s_{\text{togo},i}) \end{equation}$ | (13) |
The task for the velocity tracking is to track the reference velocity trajectory $v_{\text{ref}}$ with the angle of attack as the control variable. First,neglecting the second order term of $\omega$,the differential equation for the velocity in (4) can be expressed as
| $\begin{align} \dot{v}&=-D-g\sin\gamma =\nonumber\\ &-\frac{\rho v^{2}S}{2m} (1+\Delta D)C_{D}(\alpha)-g\sin\gamma, \end{align}$ | (14) |
where $\Delta D$ is the uncertainty in the drag model including errors of the atmospheric density,the lift and drag coefficients,and the vehicle mass. With the state variable $x = v$ and the control variable $u = C_{D}(\alpha)$,a first order SISO system for the velocity is obtained,which is
| $\begin{equation}\label{eq-vtrack} \left\{ \begin{aligned} \dot{x} & = B_{v}u+F_{v},\\ y & = x, \end{aligned} \right. \end{equation}$ | (15) |
where
| $\begin{equation}\label{eq-Bv} B_{v}=-\frac{\rho v^{2}S_A}{2m}(1+\Delta D), \end{equation}$ | (16) |
| $\begin{equation} F_{v}=-g\sin\gamma. \end{equation}$ | (17) |
Though an uncertain term exists in $B_{v}$,it is supposed to be bounded by
| $\begin{equation} \frac{1}{\chi_{D}}\leq\frac{B_{v}}{\hat{B}_{v}}\leq\chi_{D}, \end{equation}$ | (18) |
where $\hat{B}_{v}$ is the estimation of $B_{v}$ and computed by setting $\Delta D$ to be zero in(16).
To overcome the uncertainty,the SMC theory is to be used in the tracking law design. Define the sliding surface
| $\begin{equation}\label{eq-sv} s=x-x_{\text{ref}}. \end{equation}$ | (19) |
Combining with (15),we have
| $\begin{equation}\label{eq-dotsv} \dot{s}=B_{v}u+F_{v}-\dot{x}_{\text{ref}}. \end{equation}$ | (20) |
Hence,the control law based on SMC is given by
| $\begin{equation}\label{eq-uv} u=\frac{1}{\hat{B}_{v}}[\dot{x}_{\text{ref}}-F_{v}-k_{v}\text{sgn}(s)]. \end{equation}$ | (21) |
Substituting (21) into (20),we have
| $\begin{equation}\label{eq-dotsv2} \dot{s}=\left(1-\frac{B_{v}}{\hat{B}_{v}}\right)(F_{v}-\dot{x}_{\text{ref}})-\frac{B_{v}}{\hat{B}_{v}}k_{v}\text{sgn}(s), \end{equation}$ | (22) |
where $k_v$ is designed as
| $\begin{equation}\label{eq-kv} k_{v}=0.6\chi_D+(\chi_{D}-1)|\dot{x}_{\text{ref}}-F_{v}|. \end{equation}$ | (23) |
By substituting (23) into (22),it can be proved that the sliding condition is satisfied as
| $\begin{equation} \frac{1}{2}\frac{\text{d}}{\text{d}t}s^{2}=\dot{s}\cdot s\leq-0.6|s|. \end{equation}$ | (24) |
To reduce the chattering,the saturation function is employed and the control law is replaced by (25),where $\Omega_v$ is the boundary layer thickness for the velocity tracking,and is set in a time varying form $\Omega_v = 0.01v$.
| $\begin{equation}\label{eq-uv2} u=\frac{1}{\hat{B}_{v}}[\dot{x}_{\text{ref}}-F_{v}-k_{v}\text{sat}(\frac{s}{\Omega_v})] \end{equation}$ | (25) |
At last,the guidance command for the angle of attack can be computed from $C_D (\alpha) = u$.
C. Altitude Tracking LawThe task for the altitude tracking is to track the reference altitude trajectory $h_{\text{ref}}$ with the bank angle as the control variable. From (1),the differential equation for the altitude is
| $\begin{equation} \dot{h}=v\sin\gamma. \end{equation}$ | (26) |
By a further derivation and combining with (4) and (5),the second order differential of altitude is expressed as
| $\begin{equation}\label{eq-ddoth} \ddot{h}=B_h \cos\sigma+F_h, \end{equation}$ | (27) |
where
| $\begin{equation}\label{eq-Bh} B_h=L(1+\Delta L)\cos\gamma, \end{equation}$ | (28) |
| $\begin{align}\label{eq-Fh} F_h= & -D(1+\Delta D)\sin\gamma -g+\frac{v^2\cos ^2\gamma}{r}+\nonumber\\ & 2\omega v \cos\phi \sin\psi \cos\gamma, \end{align}$ | (29) |
where $\Delta L$ and $\Delta D$ are the uncertainties in the lift and drag models,respectively.
Equation (30) establishes the relation between bank angle and altitude. With the state variable $x=h$ and the control variable $u = \cos\sigma$,a second order SISO system for the altitude is obtained,i.e.,
| $\begin{equation}\label{eq-htrack} \left\{ \begin{aligned} \ddot{x} & = B_{h} u+F_{h},\\ y & = x, \end{aligned} \right. \end{equation}$ | (30) |
where $B_h$ and $F_h$ are supposed to be bounded by
| $\begin{equation} \frac{1}{\chi_L}\leq\frac{B_h}{\hat{B}_h}\leq\chi_L, \end{equation}$ | (31) |
| $\begin{equation} |F_h-\hat{F}_h|\leq\delta_h, \end{equation}$ | (32) |
where $\hat{B}_h$ and $\hat{F}_h$ are estimations of $B_h$ and $F_h$,and can be calculated by setting $\Delta L$ and $\Delta D$ to be zero in (28) and (29),respectively.
Then,define the sliding surface
| $\begin{equation}\label{eq-sh} s=\dot{x}-\dot{x}_{\text{ref}}+\lambda(x-x_{\text{ref}}). \end{equation}$ | (33) |
Combining with (30),we have
| $\begin{equation}\label{eq-dotsh} \dot{s}=B_{h}u+F_{h}-\ddot{x}_{\text{ref}}+\lambda(\dot{x}-\dot{x}_{\text{ref}}). \end{equation}$ | (34) |
Similar to the velocity tracking law,the SMC theory and the saturation function are employed,and the tracking law for the altitude is given by
| $\begin{equation} u=\frac{1}{\hat{B}_{h}}[\ddot{x}_{\text{ref}}-\hat{F}_{h}-\lambda(\dot{x}-\dot{x}_{\text{ref}})-k_h\text{sat}(\frac{s}{\Omega_h})], \end{equation}$ | (35) |
where $\Omega_h$ is the boundary layer thickness for the altitude tracking and set in a time varying form $\Omega_h= 0.012v$,and $k_h$ is designed as
| $\begin{equation} k_{h}=(\delta_h+0.5)\chi_L+(\chi_{L}-1)|\ddot{x}_{\text{ref}}-\hat{F}_{h}-\lambda(\dot{x}-\dot{x}_{\text{ref}})|. \end{equation}$ | (36) |
Finally,the guidance command for bank angle is given by $\sigma =\arccos u$.
IV. SIMULATIONS AND ANALYSISA model for the gliding reentry vehicle is used in simulations to test the decoupling trajectory tracking method presented in this study. The reentry initial conditions are as fell $h_0$ = 75km,$v_0$ = 7200m/s,$\theta_0$ = 10deg,$\phi_0$ = 0deg,$\gamma_0$ = $-$0.5deg,$\psi_0$ = 49deg,$s_{\text{togo},0}$ = 11127km. The terminal conditions are: $h_f$ = 40km,$v_f$ = 2950m/s,$|\Delta\psi_f|\leq$ 5deg,and $s_{\text{togo},f}$ = 150km. The flight constraints are: $Q_{\max}$ = 3MW/m$^2$,$n_{\rm max}$ = 3g,$q_{\rm max}$ = 100kPa. Other parameters in the trajectory tracking laws are configured as $\chi_L=\chi_D$ = 1.6,$\delta_h$ = 0.5.
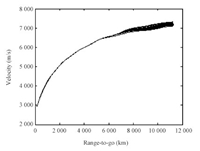
A. Simulations for RobustnessSimulations of reentry flight in dispersed cases are performed to test the robustness of the trajectory tracking method. Typical dispersions for reentry initial conditions and aerodynamic parameters are configured in Table I. With these dispersions,the Monte Carlo simulations are employed for a total of 1000 cases of reentry flight. The altitude and velocity histories with $s_{\text{togo}}$ as the independent variable are shown in Figs.4 and 5,respectively. It is seen that the decoupling method is effective on both tracking speed and tracking accuracy for both altitude and velocity trajectories.
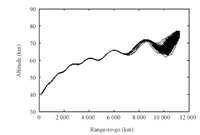
|
Download:
|
| Fig. 4. Altitude histories for 1000 dispersed cases. | |
|
Download:
|
| Fig. 5. Velocity histories for 1000 dispersed cases. | |
|
|
Table I DISPERSIONS IN MONTE CARLO SIMULATIONS |
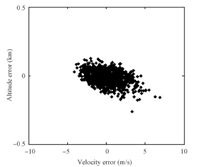
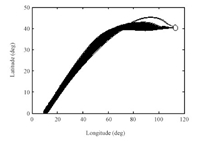
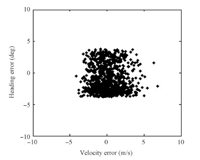
Fig.6 expresses the distribution for the terminal velocity-altitude errors in the 1000 dispersed cases. The altitude errors are kept in 0.3km,and the velocity errors are kept in 10m/s. The ground tracks for the 1000 dispersed cases are shown in Fig.7,which indicates that the lateral guidance performs well. The distribution for the terminal heading errors is shown in Fig.8. It is seen that the heading errors are kept within $\pm$ 5 deg,which indicates that the terminal constraint is well satisfied.
|
Download:
|
| Fig. 6. Terminal $h-v$ errors for 1000 dispersed cases. | |
|
Download:
|
| Fig. 7. Ground tracks for 1000 dispersed cases. | |
|
Download:
|
| Fig. 8. Terminal heading errors for 1000 dispersed cases. | |
The trajectory tracking law based on LQR is another simply designed method and has been used in many studies[9, 19, 20, 21]. Simulations in the same specific conditions are performed to compare the decoupling guidance method based on SMC with the conventional guidance method based on LQR.
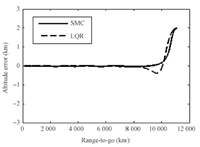
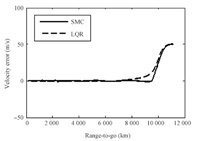
First,the two methods are simulated with dispersions for the flight initial condition $\Delta h_0$ = 2km and $\Delta v_0$ = 50m/s. Figs.9 and 10 record the altitude error histories for the two methods. Although both methods can reduce the altitude error and the velocity error to zero at the reentry terminal,the SMC method has an advantage in the convergence speed.
|
Download:
|
| Fig. 9. Comparison of the altitude errors for two methods. | |
|
Download:
|
| Fig. 10. Comparison of the velocity errors for two methods. | |
Secondly,the two methods are simulated in four conditions with different dispersions for the lift and drag coefficients. Simulation results are shown in Tables II and III. For the decoupling SMC method,the terminal altitude errors are within 0.2km and the terminal velocity errors are in within 5m/s. However,for the conventional LQR method,the terminal errors in the first three conditions are acceptable,but divergence appears in the last condition. Hence,compared with the conventional LQR method,the proposed decoupling approach based on SMC has the better anti-interference ability for the aerodynamic dispersions.
|
|
Table II SIMULATION RESULTS FOR THE DECOUPLING SMC METHOD |
|
|
Table III SIMULATION RESULTS FOR THE CONVENTIONAL LQR METHOD |
In summary,the new decoupling SMC approach is more effective than the conventional LQR approach.
V. CONCLUSIONIn this paper,the traditional multi-objective tracking problem for the reentry trajectory is separated into the altitude tracking and the velocity tracking,and both of the tracking laws are designed with the SMC theory. From Monte Carlo simulations of 1000 dispersed cases,the decoupling tracking method is shown to be robust to the uncertain reentry conditions. From the comparison with the conventional LQR method,it is indicated that the decoupling tracking law owns better performance in the convergence speed and the anti-interference ability for large dispersions.
With the decoupling strategy presented in this paper,the trajectory tracking algorithm for the reentry vehicle is significantly simplified. In future works,other control theories for a SISO system can be applied to the altitude tracking law and the velocity tracking law based on this decoupling strategy.
| [1] | Xu B, Sun F, Liu H, Ren J. Adaptive Kriging controller design for hypersonic flight vehicle via back-stepping. IET Control Theory and Applications, 2012, 6(4):487-497 |
| [2] | Yang J, Li S H, Sun C Y, Guo L. Nonlinear-disturbance-observer-based robust flight control for airbreathing hypersonic vehicles. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2):1263-1275 |
| [3] | Stewart J D, Greenshields D H. Entry vehicles for space programs. Journal of Spacecraft and Rockets, 1969, 6(10):1089-1102 |
| [4] | Sun Chang-Yin, Mu Chao-Xu, Yu Yao. Some control problems for near space hypersonic vehicles. Acta Automatica Sinica, 2013, 39(11):1901-1913(in Chinese) |
| [5] | Bao Wei-Min. Present situation and development tendency of aerospace control techniques. Acta Automatica Sinica, 2013, 39(6):697-702(in Chinese) |
| [6] | Harpold J C, Graves C A. Shuttle entry guidance. Journal of the Astronautical Sciences, 1979, 27(3):239-268 |
| [7] | Lu P. Entry guidance and trajectory control for reusable launch vehicle. Journal of Guidance, Control, and Dynamics, 1997, 20(1):143-149 |
| [8] | Lu P. Regulation about time-varying trajectories:precision entry guidance illustrated. Journal of Guidance, Control, and Dynamics, 1999, 22(6):784-790 |
| [9] | Dukeman G A. Profile-following entry guidance using linear quadratic regulator theory. In:Proceedings of the 2002 AIAA Guidance, Navigation, and Control Conference and Exhibit. Monterey, USA:AIAA, 2002. 2002-4457 |
| [10] | Mooij E. Model reference adaptive guidance for re-entry trajectory tracking. In:Proceedings of the 2004 AIAA Guidance, Navigation, and Control Conference and Exhibit. Providence, USA:AIAA, 2004. 2004-4900 |
| [11] | Zhang Jun, Xiao Yu-Zhi, Bi Zhen-Fa. Guidance method based on multimodel prediction for re-entry vehicles. Acta Aeronautica et Astronautic Sinica, 2008, 29(Sup):S20-S25(in Chinese) |
| [12] | Benito J, Mease K D. Nonlinear predictive controller for drag tracking in entry guidance. In:Proceedings of the 2008 AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Honolulu, USA:AIAA, 2008.2008-7350 |
| [13] | Pu Z Q, Tan X M, Fan G L, Yi J Q. Design of entry trajectory tracking law for a hypersonic vehicle via inversion control. In:Proceedings of the 10th World Congress on Intelligent Control and Automation. Beijing, China:IEEE, 2012. 1092-1097 |
| [14] | Zhu Kai. Study of Reentry Guidance and Control Algorithm for Glide Missile[Ph. D. dissertation], Harbin Institute of Technology, China, 2011. (in Chinese) |
| [15] | Desiderio D, Lovera M. Guidance and control for planetary landing:flatness-based approach. IEEE Transactions on Control Systems Technology, 2013, 21(4):1280-1294 |
| [16] | Vinh N X, Busemann A, Culp R D. Hypersonic and Planetary Entry Flight Mechanics. Ann Arbor, MI:University of Michigan Press, 1980. 26-28 |
| [17] | Xue S B, Lu P. Constrained predictor-corrector entry guidance. Journal of Guidance, Control, and Dynamics, 2010, 33(4):1273-1281 |
| [18] | Li H F, Zhang R, Li Z Y, Zhang R. New method to enforce inequality constraints of entry trajectory. Journal of Guidance, Control, and Dynamics, 2012, 35(5):1662-1667 |
| [19] | Li Yu. Study of Trajectory Optimization and Guidance Algorithm for Boost-Glide Missile[Ph. D. dissertation], Harbin Institute of Technology, China, 2009(in Chinese) |
| [20] | Liang Z X, Ren Z, Bai C. Lateral reentry guidance for maneuver glide vehicles with geographic constraints. In:Proceedings of the 32nd Chinese Control Conference. Xi'an, China:IEEE, 2013. 5187-5192 |
| [21] | Zhou W, Tan S, Chen H. A simple reentry trajectory generation and tracking scheme for common aero vehicle. In:Proceedings of the 2012 AIAA Guidance, Navigation, and Control Conference. Minneapolis, USA:AIAA, 2012. 2012-4709 |
 2015, Vol.2
2015, Vol.2 


