THE attitude control of a rigid body has been extensively studied in the past years. It is a very interesting problem due to its importance in nonlinear control theory and different applications in engineering,such as slewing and pointing of spacecrafts,helicopters,satellites,underwater vehicles and robot manipulation.
The attitude stabilization problem of a rigid body has been investigated by many researchers,and different nonlinear control methods have been proposed,such as adaptive control[1],hybrid control[2],PD+ control[3]. Among the existing results,most are asymptotically stable ones[1, 2, 3, 4, 5, 6, 7],which imply that the state trajectories of the system converge to its equilibrium as time goes to infinity.
However,there is little literature about finite-time attitude control of a rigid body. Obviously,finite-time stabilization of a system makes it possible to achieve higher-precision performance and better disturbance rejection properties[8, 9, 10]. For example,the terminal sliding mode control method employed in [9] guaranteed finite-time reachability of given desired attitude of a rigid spacecraft,but the proposed control law had a singularity problem. In [10],by the method of adding a power integrator,a finite-time attitude tracking control law using both attitude and angular velocity was designed. A distributed finite-time containment control scheme was reported in [11].
The existing finite-time attitude control laws mainly depend on the methods explored in the study for general nonlinear systems. Usually these control laws are obtained by complicated calculation and are not easy to understand. In this case,using the inherent properties of system to simplify the designing process might be possible and desirable.
The attitude control with the feedback of full state measurements (i.e.,attitude and angular velocity) has been changed to the control without the requirement of the angular velocity measurement due to the lack of tachometer of manipulators[6, 7, 12, 13, 14, 15, 16]. This design process is based on the passivity property established for attitude motion of a rigid body. Egeland and Godhavn[7] derived the adaptive attitude control law for robotic manipulators based on the idea of passivity. Tsiotras[15] showed that linear asymptotically stabilizing control laws without angular velocity measurements could be obtained naturally and easily from the passivity properties. The stabilization control method proposed in [16] used an auxiliary dynamical system to replace the angular velocity feedback. For multiple rigid bodies$'$ case,Ren[17] used a similar idea to derive distributed passivity-based control laws.
Different from the existing finite-time attitude control methods,our approach focuses on designing a finite-time attitude control law based on the passivity properties of the attitude motion of a rigid body. We define the finite-time passivity for general nonlinear systems and derive stability criterion for finite-time strictly passive systems. Also,we obtain different nonlinear finite-time control laws for different classes of passive systems. Based on the above results,by combining with sliding mode control approach and the properties of finite-time passivity,a finite-time attitude controller is proposed. To the best of authors$'$ knowledge,this is a new solution to the finite-time attitude control problem. The proposed approach naturally expands the properties for passive systems and may provide a tool for the study of general nonlinear systems.
The paper is organized as follows. In Section II,some preliminaries and problem formulation are given. In Section III,the finite-time passivity for dynamical systems is defined,and for the attitude set point control problem,a finite-time attitude control law is derived. Some finite-time passivity properties of the feedback connection system are shown in Section IV. In Section V,numerical simulations are given to illustrate the results. Finally,we make conclusion in Section VI.
II. PRELIMINARIES AND PROBLEM FORMULATION A.Rotation Motion of a Rigid BodyIt is fundamental and important to select a nonsingular parameterization for attitude. Modified Rodrigues parameters (MRPs) are a popular parameterization of three-dimensional coordinate expression[18]. We adopt the MRPs to describe the rotation motion of a rigid body.
Let $\sigma=\eta\tan(\theta/4)\in {\bf R}^{3}$ $(-2\pi<\theta<2\pi)$ stand for the MRPs for a rigid body,where $\eta$ is the Euler axis and $\theta$ is the Euler angle. For a three-dimensional vector $\nu=[\nu_{1},\nu_{2},\nu_{3}]^{\rm T}$,symbol $s(\nu)=[0,\nu_{3},-\nu_{2};-\nu_{3},0,\nu_{1};\nu_{2},-\nu_{1},0]$. The cross product of two vectors can be denoted by the multiplication of a skew-symmetric matrix and a vector,that is to say,$s(a)b=-a\times b$,$a,b\in{\bf R}^3$. Let $u(t)\in{\bf R}^3$ be an external control torque vector acting on the rigid body. The mass moment of inertia is denoted by the positive and symmetric matrix $J\in{\bf R}^{3\times3}$ which can be usually transformed to a diagonal matrix. $\omega(t)\in {\bf R}^{3}$ is the angular velocity of rigid body with respect to the inertial frame expressed in the body frame. $I_{3}$ denotes the $3\times3$ identity matrix. The attitude kinematics and dynamics of a rigid body are
| $\dot{\sigma}=G(\sigma)\omega,$ | (1a) |
| $J\dot\omega=s(\omega)J\omega+u,$ | (1b) |
where
| $G(\sigma)=\frac{1}{2} \left[\frac{1-\sigma^{\rm T}\sigma}{2} I_{3} -s(\sigma)+ \sigma\sigma^{\rm T}\right].$ | (2) |
From [14],some useful properties for $G(\sigma)$ are as follows:
| $\sigma^{\rm T} G(\sigma) \omega=\frac{1+\sigma^{\rm T}\sigma}{4} \sigma^{\rm T}\omega,\quad G(\sigma)G^{\rm T}(\sigma)=\frac{1+\sigma^{\rm T}\sigma}{4} I_{3}.$ | (3) |
Now we introduce the definitions and properties of passive system.
B.PassivityDefinition 1[19]. Consider a dynamical system represented by
| $\dot{x}=f(x,u),$ | (4a) |
| $y=h(x,u),$ | (4b) |
where $f:{\bf R}^n\times{\bf R}^n\rightarrow{\bf R}^n$ is locally Lipschitz,$h:{\bf R}^n\times{\bf R}^n\rightarrow{\bf R}^n$ is continuous,$f(0,0)=0$,and $h(0,0)=0$.
The system is said to be passive if there exists a continuously differentiable positive semi definite function $V(x)$ (called the storage function) such that
| $u^{\rm T}y \geq \dot V = \frac{\partial V}{\partial x} f(x,u),\quad \forall (x,u)\in {\bf R}^{n} \times {\bf R}^{n}.$ |
Moreover,it is said to be
1) lossless if $u^{\rm T}y=\dot{V}$;
2) output feedback passive if $u^{\rm T}y\geq\dot{V}+y^{\rm T}\rho(y)$ for some function $\rho$;
3) output strictly passive if $u^{\rm T}y\geq\dot{V}+y^{\rm T}\rho(y)$ and $y^{\rm T}\rho(y)>0$,$\forall y\neq0$;
4) strictly passive if $u^{\rm T}y\geq\dot{V}+\Psi(x)$ for some positive definite function $\Psi$.
In all cases,the inequalities should hold for all ($x,u$).
The definition of zero-state observability is quite useful in stating the following stability criterion for strictly passive system.
Definition 2[19]. The system (4a) and (4b) is said to be zero-state observable,if no solution of $\dot{x}=f(x,0)$ can stay identically in $S=\{x\in{\bf R}^n|h(x,0)=0\}$,other than the trivial solution $x(t)\equiv0$.
Lemma 1[19]. Consider system (4a) and (4b),the origin of $\dot{x}=f(x,0)$ is asymptotically stable if one of the following statements is satisfied:
1) The system is strictly passive;
2) The system is output strictly passive and zero-state observable.
Furthermore,if the storage function is radially unbounded,the origin will be globally asymptotically stable.
If we require the storage function to be positive definite,one can obtain the following control law to globally asymptotically stabilize the origin of a nonlinear dynamical system.
Lemma 2[19]. If system (4a) and (4b) is
1) passive with a radially unbounded positive definite storage function;
2) zero-state observable.
Then the origin $x=0$ can be globally stabilized by the control $u=-\varphi(y)$,where $\varphi$ is any locally Lipschitz function such that $\varphi(0)=0$ and $y^{\rm T}\varphi(y)>0$ for all $y\not=0$.
In essence,the design procedure of a finite-time control law for a dynamical system is a process to make sure the trajectories of the states of closed-loop system reach desired points in finite time. The corresponding properties are described by finite-time stability.
C.Finite-time StabilityLemma 3[20]. Consider the system $\dot{x}=f(x)$,where the continuous function $f(\cdot):{\bf R}^n\rightarrow{\bf R}^n$ satisfies $f(0)=0,x\in {\bf R}^{n}$. Suppose there exists a continuous,positive definite storage function $V(x):D\rightarrow{\bf R},$ real numbers $\alpha\in(0,1)$ and $c>0$,such that $\dot{V}(x)+c(V(x))^{\alpha}\leq0$ on $D$,where $D$ is an open neighborhood of the origin,then the origin of system $\dot{x}=f(x)$ is finite-time stable. Moreover,if $T$ is the settling time,then $T\leq(V(x))^{1-\alpha}/(c(1-\alpha))$. The origin is said to be globally finite-times stable if it is finite-time stable and $D={\bf R}^n$.
Remark 1. The statement that the origin of system $\dot{x}=f(x)$ is finite-time stable means that the state variables reach the origin in finite time.
Lemma 4[21]. For any $x_{i}\in{\bf R}~(i=\{1,\cdots,n\})$,the following inequality is satisfied:
| $(|x_{1}|+\cdots+|x_{n}|)^{p}\!\!\leq\!\!|x_{1}|^{p}+\cdots+|x_{n}|^{p}\!\!\leq\!\!n^{1-p}(|x_{1}|+\cdots+|x_{n}|)^{p}$ |
for any real number $p\in(0,1]$.
D.Problem FormulationGiven the system described by (1a) and (1b),the control aim is to design a finite-time control law which guarantees the attitude of a rigid body tracks the desired steady attitude target in finite time.
III. FINITE-TIME PASSIVITY AND ATTITUDE SET POINT CONTROL A.Finite-time PassivityLyapunov stability is related nicely to passivity with the positive storage (energy) function. Since the requirements of the storage function in the definition of finite-time stability is stricter than Lyapunov function,it is natural for us to explore unique finite-time properties for a passive system.
Definition 3(Finite-time passivity). Consider the system described by (4a) and (4b),
| $\dot{x}=f(x,u),$ |
| $y=h(x,u).$ |
The system is said to be finite-time strictly passive if there exists a continuously differentiable positive semi definite function $V(x)$ (called the storage function) such that
| $u^{\rm T}y\geq\dot{V}+cV^{\alpha},$ |
for some $\alpha\in(0,1)$ and $c>0$.
The finite-time stability of the origin of a system is determined by the finite-time passivity of the system. The results are as follows.
Theorem 1. Consider the system (4a) and (4b),if the system is finite-time strictly passive,then the origin of $\dot{x}=f(x,0)$ is finite-time stable. Furthermore,if storage function $V(x)$ is radially unbounded,the origin will be globally finite-time stable.
The proof of Theorem 1 is in Appendix.
Remark 2. Theorem 1 can be viewed as a stability criterion for a finite-time strictly passive system. If a passive system (4a) and (4b) is lossless,the origin of the closed-loop system will be finite-time stable once the control law is designed properly to make the closed-loop system finite-time strictly passive.
Example. Consider the integrator system
| $\dot{x}=u,$ | (5) |
where $x\in {\bf R}^{n}$,$u\in {\bf R}^{n}$. Suppose the output system is
| $y=x,$ |
where $y\in {\bf R}^{n}.$ Choose the storage function as
| $V_{0}(x)=\frac{1}{2}x^{\rm T}x.$ |
Taking the time derivative of the storage function along the trajectories of (5) yields
| $\dot{V_{0}}(x)=u^{\rm T}y.$ |
So the system is lossless.
Suppose the feedback to be designed is $h_{0}(x)\in {\bf R}^{n}$,then the closed-loop system is
| $\dot{x}=u=r-h_{0}(x),$ |
where $r\in {\bf R}^{n}$ is the input. Then we get
| $r^{\rm T}y=\dot{V_{0}}+x^{\rm T}h_{0}(x).$ |
So we have
| $c_{0}V_{0}^{\alpha_{0}}=c_{0}\left(\frac{1}{2}\right)^{\alpha_{0}}\left(\sum\limits_{i=1}^{n} x_{i}^{2}\right)^{\alpha_{0}}\leq c_{0}\left(\frac{1}{2}\right)^{\alpha_{0}}\sum\limits_{i=1}^{n} x_{i}^{2\alpha_{0}},$ |
for some real numbers $\alpha_{0}\in(0,1)$ and $c_{0}>0$.
Suppose
| $h_{0}(x)=c_{0}\left(\frac{1}{2}\right)^{\alpha_{0}}x^{2\alpha_{0}-1}.$ | (6) |
Then
| $r^{\rm T}y\geq\dot{V_{0}}+c_{0}V_{0}^{\alpha_{0}}.$ |
The closed-loop system is finite-time strictly passive for input $r$ and output $y$ according to Definition 3. From Theorem 1,the origin of the autonomous closed-loop system is finite-time stable.
The corresponding control law is
| $u=-h_{0}(x)=-c_{0}\left(\frac{1}{2}\right)^{\alpha_{0}}x^{2\alpha_{0}-1}.$ | (7) |
Based on the above results,it is possible to derive finite-time control laws for certain passive systems.
Theorem 2. Consider the system described by
| $\dot{x}=f(x,u),$ | (8a) |
| $y=x,$ | (8b) |
where $f:{\bf R}^n\times{\bf R}^n\rightarrow{\bf R}^n$ is locally Lipschitz,$f(0,0)=0$,for some real numbers $\alpha\in(0,1)$ and $c>0$.
1) If the system is lossless with storage function $V=2\ln(1+x^{\rm T}x)$,choosing $V$ as the candidate Lyapunov function,the origin of the system is finite-time stable with control law $u=-c\cdot2^{\alpha}\cdot x^{2\alpha-1}$.
2) If the system is lossless with storage function $V=\frac{1}{2}x^{\rm T}Jx$,where the diagonal matrix $J={\rm diag}\{J_{1},J_{2},\cdots,J_{n}\}$ is positive definite,choosing $V$ as the candidate Lyapunov function,then the origin of the system is finite-time stable with control law $u=-c\cdot(\frac{1}{2})^{\alpha}\cdot J^{\alpha}\cdot x^{2\alpha-1}$.
Proof.
1) Since the system is lossless,we will design a state feedback to make the closed-loop system finite-time strictly passive. Suppose $r$ is the input and $h(x)=[h_{1}(x),h_{2}(x),\cdots,h_{n}(x)]^{\rm T}\in {\bf R}^{n}$ is the state feedback to be designed.
The closed-loop system is
| $\dot{x}=f(x,r-h(x)),$ |
| $y=x.$ |
If we choose
| $h_{i}(x)=c\cdot2^{\alpha}\cdot x_{i}^{2\alpha-1},$ |
then
| $r^{\rm T}y=(u+h(x))^{\rm T}x=u^{\rm T}x+c\cdot2^{\alpha}\cdot\sum\limits_{i=1}^{n} x_{i}^{2\alpha}.$ |
By Lemma 4,we have
| $\begin{array}{l} {({x^{\rm{T}}}x)^\alpha } = {(x_1^2 + \cdots + x_n^2)^\alpha } \le \sum\limits_{i = 1}^n {x_i^{2\alpha }} = \quad \\ ({x_1},\cdots ,{x_n}) \cdot \left( {\begin{array}{*{20}{c}} {x_1^{2\alpha - 1}}\\ \vdots \\ {x_n^{2\alpha - 1}} \end{array}} \right). \end{array}$ |
So we get
| $r^{\rm T}y\geq u^{\rm T}x+c\cdot2^{\alpha}\cdot (x^{\rm T}x)^{\alpha}.$ |
Since the system is lossless,i.e.,
| $u^{\rm T}y=\dot{V},$ |
we get
| $r^{\rm T}y\geq\dot{V}+c\cdot2^{\alpha}\cdot (x^{\rm T}x)^{\alpha}.$ |
Using
| $x^{\rm T}x\geq\ln(1+x^{\rm T}x),$ |
we get
| $r^{\rm T}y\geq\dot{V}+c\cdot V^{\alpha}.$ |
Choosing $V$ as the Lyapunov candidate function,then the closed-loop system is finite-time strictly passive. Based on Theorem 1,when input $r=0$,the origin is finite-time stable. So the corresponding control law is
| $u=-c\cdot2^{\alpha}\cdot x^{2\alpha-1}.$ |
2) The proof for case 2) is similar to case 1),thus omitted.
Remark 3. According to Lemma 4,the index $2\alpha-1$ should belong to interval (0,1]. In addition,the definition of finite-time stability (Lemma 3) requires $\alpha\in(0,1)$. Combining two inequalities,we have that $\alpha$ should belong to interval (1/2,1).
It is very important to notice that the kinematics equation (1a) and dynamics equation (1b) describe two passive systems,respectively.
Proposition 1[15].
1) System (1a) is lossless with input $\omega$ and output $\sigma$.
2) System (1b) is lossless with input $u$ and output $\omega$.
Proof.
1) Taking the time derivative of function $V_{1}(\sigma)=2{\rm ln}(1+\sigma^{\rm T}\sigma)$ along the trajectories of (1a) yields that $\dot V_{1}(\sigma)=\sigma^{\rm T}\omega$. This shows the system is passive (lossless).
2) Taking the time derivative of function $V_{2}(\omega)=\frac{1}{2}\omega^{\rm T}J\omega$ along the trajectories of (1b) yields that $\dot V_{2}(\omega)=\omega^{\rm T}u$. This shows the system is passive (lossless).
From Theorem 2,we obtain the finite-time control laws for subsystems (1a) and (1b),respectively.
Proposition 2. If we can find real numbers satisfying $\alpha_{1}\in(1/2,1)$ and $c_{1}>0$,then the origin of system (1a) is finite-time stable with control
| $\left(\begin{array}{ccc} \omega_{1} \\ \omega_{2}\\ \omega_{3} \\ \end{array} \right)=-c_{1}\cdot2^{\alpha_{1}}\cdot \left(\begin{array}{ccc} \sigma_{1}^{2\alpha_{1}-1} \\ \sigma_{2}^{2\alpha_{1}-1} \\ \sigma_{3}^{2\alpha_{1}-1} \\ \end{array} \right).$ | (9a) |
If we can find real numbers satisfying $\alpha_{2}\in(1/2,1)$ and $c_{2}>0$,then the origin of system (1b) is finite-time stable with control
| $\left(\begin{array}{ccc} u_{1} \\ u_{2}\\ u_{3}\\ \end{array} \right)=-c_{2}\cdot(\frac{1}{2})^{\alpha_{2}} \cdot J^{\alpha_{2}} \left(\begin{array}{ccc} \omega_{1}^{2\alpha_{2}-1} \\ \omega_{2}^{2\alpha_{2}-1} \\ \omega_{3}^{2\alpha_{2}-1} \\ \end{array} \right).$ | (9b) |
Let $\omega_{d},\sigma_{d}$ represent the desired angular velocity and attitude,respectively. Define $e=[e_{1},e_{2},e_{3}]^{\rm T}\in{\bf R}^{3}$ as the relative attitude error between the actual attitude and the desired attitude,where
| $e=\sigma\otimes\sigma_{d}^{-1}=\frac{\sigma_{d}(\sigma^{\rm T}\sigma-1)+\sigma(1-\sigma_{d}^{\rm T}\sigma_{d})+2s(\sigma_{d})\sigma}{1+\sigma_{d}^{\rm T}\sigma_{d}\sigma^{\rm T}\sigma+2\sigma_{d}^{\rm T}\sigma}.$ |
In order to describe the relative angular velocity error,the desired reference frame should be transformed to the body frame. Denote the transform matrix is $R_{d}^{b}$,which is proper and orthogonal. Then $R_{d}^{b}=R(e)$ is given by
| $R(e)=I_{3}+4((1-e^{\rm T}e)/(1+e^{\rm T}e)^{2})s(e)+8s^{2}(e)/(1+e^{\rm T}e)^{2}.$ |
The relative angular velocity error is then represented by
| $\xi=[\xi_{1},\xi_{2},\xi_{3}]^{\rm T}=\omega-R_{d}^{b}\omega_{d}\in{\bf R}^3.$ |
The relative kinematic and dynamic equations are given as[10]
| $\dot e=G(e)\xi,$ |
| $J\dot\xi=s(\omega)J\omega+u-JR_{d}^{b}\dot\omega_{d}-Js(\xi)R_{d}^{b}\omega_{d}.$ |
This paper studies the set point control problem for a rigid body. In this case,$\omega_{d}=0,~\dot\omega_{d}=0.$ So the whole system is represented by
| $\dot e=G(e)\omega,$ | (10a) |
| $J\dot\omega=s(\omega)J\omega+u.$ | (10b) |
Therefore,we need to design control torque $u$ which makes relative error $e$ goes to zero in finite time.
The relative attitude kinematics and dynamics rotation equations (10a) and (10b) represent a system in cascade form. Control torque $u$ drives the dynamical equation and angular velocity $\omega$ drives the kinematic equation. For systems in cascade connection,it is easy to use a two-step methodology to achieve closed-loop stability. First,we choose a proper sliding surface,concentrating on the stabilization of the kinematic equation treating the driving state (the angular velocity vector) as a control-like variable. Second,we proceed to the stabilization of the dynamical system to the desired state calculated in the first step treating control torque $u$ as the driving state,driving the motion of the system to the proposed sliding surface in finite time.
Theorem 3. For system (10a) and (10b),if control torque $u$ is chosen as
| $\begin{array}{*{20}{l}} {u = }&{ - s(\omega )J\omega - {k_v} \cdot {{(\frac{1}{2})}^{{p_2}}} \cdot {J^{{p_2}}} \cdot {{(\omega - {\omega ^*})}^{2{p_2} - 1}} - }\\ {}&{{k_p} \cdot (2{p_1} - 1) \cdot {2^{{p_1}}} \cdot (J \cdot {e^{2{p_1} - 2}})^\circ (G(e) \cdot \omega ),} \end{array}$ | (11) |
where $\omega^{*}=-k_{p}\cdot2^{p_{1}}\cdot e^{2p_{1}-1}$,$k_{v}>0,k_{p}>0$,$1/2<p_{1},p_{2}<1,$ symbol $\circ$ denotes the Hadamard product. Then $e$ converges to zero in finite time.
Proof.
The proof consists of two steps. First,angular velocity $\omega$ is treated as the input for (10a) and is developed to make $e$ converge to zero in finite time. Select the sliding surface to be $z=\omega-\psi(e)$ such that when state trajectory of the system is restricted to the surface,the reduced-order model $\dot e=G(e)\psi(e)$ has a finite-time stable origin. Next,control torque $u$ is calculated in order that sliding surface $z=\omega-\psi(e)$ goes to zero in finite time and remains there for all future time.
Step 1. Angular velocity $\omega$ design
The storage function is chosen as
| $V_{0}=2\ln(1+e^{\rm T}e)$ |
along the trajectory of (10a),and using (3) we have
| $\dot V_{0}=\frac{4}{1+e^{\rm T}e}e^{\rm T}\dot e=\frac{4}{1+e^{\rm T}e}e^{\rm T}G(e)\omega=e^{\rm T}\omega.$ |
By Proposition 2,we get
| $\omega=\psi(e)=-k_{p}\cdot2^{p_{1}}\cdot e^{2p_{1}-1},$ |
so we obtain
| $\dot V_{0}=-k_{p}\cdot2^{p_{1}}\sum\limits_{i=1}^{3}e_{i}^{2p_{1}}\leq-k_{p}\cdot(2\sum\limits_{i=1}^{3}e_{i}^{2})^{p_{1}},$ |
since
| $V_{0}=2\ln(1+e^{\rm T}e)\leq2e^{\rm T}e=2\sum\limits_{i=1}^{3}e_{i}^{2},$ |
and
| $\dot V_{0}+k_{p}V_{0}^{p_{1}}\leq0.$ |
By Lemma 3,$e$ and$V_{0}(t)$ converge to zero in finite time.
Step 2. Control torque $u$ design
The system describing attitude motion of a rigid body can be transformed into the form of
| $\begin{cases} \dot e=G(e)\psi(e)+G(e)(\omega-\psi(e)),\\ \dot\omega=J^{-1}s(\omega)J \omega+J^{-1}u. \end{cases}$ |
Design the sliding surface $z=\omega-\psi(e)$ and let $J^{-1}\nu=J^{-1}u-\dot\psi$,we obtain
| $\begin{cases} \dot e=G(e)\psi(e)+G(e)z,\\ \dot z=J^{-1}(s(\omega)J \omega+\nu). \end{cases}$ |
Taking $\nu=-s(\omega)J\omega+\varphi(z)$,the task is simplified to design $\varphi(z)$ to make $z$ reach zero in finite time and remain there afterwards.
Choosing the candidate Lyapunov function as $V_{1}=\frac{1}{2}z^{\rm T}Jz$,along (10b),we have $\dot V_{1}=z^{\rm T}\varphi(z)$. Taking
| $\varphi(z)=-k_{v}\cdot\left(\frac{1}{2}\right)^{p_{2}} \cdot J^{p_{2}}\cdot z^{2p_{2}-1}$ |
and by Lemma 4,we get
| $\dot V_{1}\leq -k_{v}\cdot\left(\frac{1}{2}\right)^{p_{2}} \cdot J^{p_{2}}\cdot \left(\sum\limits_{i=1}^{3}z_{i}^{2}\right)^{p_{2}}=-k_{v}\cdot V_{1}^{p_{2}}.$ |
Thus $z$ goes to zero in finite time and stays there afterwards.
Based on the above steps,we get the result proposed in Theorem 3.
IV. FINITE-TIME PASSIVITY OF FEEDBACK SYSTEMSIn this section,some finite-time passivity properties for the feedback connection system determined by the finite-time passivity property of each component are shown.
Consider the feedback connection of two finite-time passive systems in Fig. 1 represented by the state model
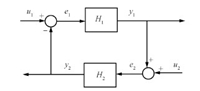
|
Download:
|
| Fig. 1. Feedback connection. | |
| $\dot{x_{i}}=f_{i}(x_{i},e_{i}),$ | (12a) |
| $y_{i}=h_{i}(x_{i},e_{i}).$ | (12b) |
We require $u_{1}$,$y_{1}$,$u_{2}$,$y_{2}$ to be vectors of the same dimension and the feedback connection to have a well-defined state model. The closed-loop state model takes the form of
| $\dot{x}=f(x,u),$ | (13a) |
| $y=h(x,u),$ | (13b) |
where $x=[x_{1},x_{2}]^{\rm T}$,$u=[u_{1},u_{2}]^{\rm T}$,$y=[y_{1},y_{2}]^{\rm T}$ and
| ${e_1} = {u_1} - {y_2},$ |
| $e_{2}=u_{2}+y_{1}.$ |
We assume that $f$ is locally Lipschitz,$h$ is continuous,and $f(0,0)=0,~h(0,0)=0.$ $V_{i}~(i=1,2)$ are the storage functions of the two subsystem,respectively. $V$ denotes the storage function of the feedback connection system as
| $V=V_{1}+V_{2}.$ |
It is known that the feedback connection of two passive systems in Fig. 1 is passive[19]. That is to say
| $u^{\rm T}y\geq \dot{V}.$ |
For the finite-time passive systems,some new definitions and notions are given as follows.
Definition 4. The feedback connection of two finite-time strictly passive systems is
1) Lyapunov strictly passive if
| $\dot{V}+c_{1}V_{1}^{\alpha_{1}}+c_{2}V_{2}^{\alpha_{2}}\leq0,$ |
for some $c_{i}>0$ and $\alpha_{i}\in(0,1)$,$i\in\{1,2\}$;
2) finite-time strictly passive if
| $\dot{V}+cV^{\alpha}\leq0,$ |
for some $c>0$ and $\alpha\in(0,1)$.
Now we are ready to present the finite-time stability of the feedback connection of finite-time strictly passive systems.
Theorem 4. The feedback connection of two finite-time strictly passive systems is Lyapunov strictly passive if input $u=0$. Furthermore,the closed-loop system is also a finite-time strictly passive system if the storage functions satisfy the following conditions:
| $\begin{cases} 0<V_{1}<1,\\ 0<V_{2}<1,\\ 0<V<1. \end{cases}$ |
Proof. Since every component is a finite-time strictly passive system,we get
| $e_{1}^{\rm T}y_{1}\geq\dot{V_{1}}+c_{1}V_{1}^{\alpha_{1}},$ |
| $e_{2}^{\rm T}y_{2}\geq\dot{V_{2}}+c_{2}V_{2}^{\alpha_{2}}.$ |
From the feedback connection,we see that
| $\begin{array}{l} e_1^{\rm{T}}{y_1} + e_2^{\rm{T}}{y_2} = {({u_1} - {y_2})^{\rm{T}}}{y_1} + {({u_2} + {y_1})^{\rm{T}}}{y_2} \ge \quad \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{V_1}}\limits^. + {c_1}V_1^{{\alpha _1}} + \mathop {{V_2}}\limits^. + {c_2}V_2^{{\alpha _2}}. \end{array}$ |
Hence
| $u^{\rm T}y\geq\dot{V_{1}}+c_{1}V_{1}^{\alpha_{1}}+ \dot{V_{2}}+c_{2}V_{2}^{\alpha_{2}}.$ |
Taking
| $V(x)=V_{1}(x_{1})+V_{2}(x_{2})$ |
as the storage function for the feedback connection,we obtain
| $u^{\rm T}y\geq\dot{V}+c_{1}V_{1}^{\alpha_{1}}+c_{2}V_{2}^{\alpha_{2}}.$ |
So we know the closed-loop system is Lyapunov finite-time stable when
| $u=0.$ |
Further,if
| $\begin{cases} 0<V_{1}<1,\\ 0<V_{2}<1,\\ 0<V<1. \end{cases}$ |
we choose
| $c=\min\{c_{1},c_{2}\},$ |
| $\alpha=\min\{\alpha_{1},\alpha_{2}\}.$ |
Hence,
| $\dot{V}+c(V_{1}+V_{2})^{\alpha}=\dot{V}+cV^{\alpha}\leq0.$ |
Now the closed-loop system is finite-time strictly stable.
Remark 4.Theorem 4 shows that for the feedback connection of two finite-time strictly passive systems,the closed-loop system is also a finite-time strictly passive system for some region of the system energy.
V. NUMERICAL SIMULATIONSWe now illustrate the above results by means of some numerical simulations. We first show the effectiveness of the results of Proposition 2.
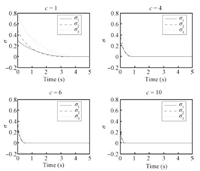
Consider system (1a),we suppose the initial MRP vector is $\sigma_{0}=[0.3,0.5,0.8]^{\rm T}$. The values for the gains are chosen as $c=1,4,6,10,$ and $\alpha=0.8$.
The results are shown in Fig. 2. Under control law (9a),the origin of system (1a) can be finite-time stabilized. The finite time $T$ will decrease as we increase the value of parameter $c$ which has the maximum value $c_{\rm max}$ satisfying $\dot{V}(x)+c_{\rm max}(V(x))^{\alpha}\leq0$.
|
Download:
|
| Fig. 2. Stabilization for system (1a). | |
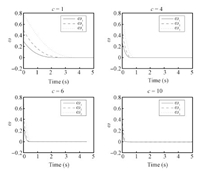
For system (1b),we suppose the initial angular velocity is $\omega_{0}=[0.3,0.5,0.8]^{\rm T}$ and the inertia matrix is represented by $J={\rm diag}\{1,0.63,0.85\}$. The values of the gains are chosen as $c=1,4,6,10,$ and $\alpha=0.8$. Fig. 3 shows that under control law (9b),the origin of system (1b) can be finite-time stabilized. The finite time $T$ will decrease as we increase the value of parameter $c$ which has the maximum value $c_{\rm max}$ satisfying $\dot{V}(x)+c_{\rm max}(V(x))^{\alpha}\leq0$.
|
Download:
|
| Fig. 3. Stabilization for system (1b). | |
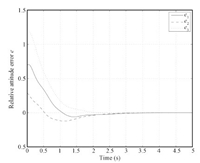
An example considered in [5] is addressed here to demonstrate the results proposed in Section III. Suppose a rigid body is with the inertia matrix (expressed in the body frame) $J={\rm diag}\{1,0.63,0.85\}$,the initial orientation corresponds to the identity matrix $I_{3}$,and the initial angular velocity is $[\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}]$. In terms of the equivalent axis and angle representation,the desired attitude target corresponds to an eigenaxis/angle representation given by
| $\eta=[0.4896,0.2032,0.8480]^{\rm T},\quad\theta=2.4648~{\rm rad}.$ |
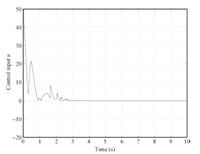
The values of the gains are selected to be $k_{p}=6$ and $k_{v}=6$. In order to satisfy the finite-time stability theorem,we select $p_{1}=0.9$ and $p_{2}=0.9$. These values are chosen by trial and error to achieve good performance. Based on control law (11),we get the following results: Fig. 4 depicts the behavior of the MRP vector,and Fig. 5 shows the time history of the corresponding control effort.
|
Download:
|
| Fig. 4. Stabilization for system (10a) and (10b). | |
|
Download:
|
| Fig. 5. Control input for system (10a) and (10b). | |
In this paper,we propose a finite-time attitude control law for a rigid body based on the finite-time passivity. Some additional finite-time passivity results for feedback connection systems are also shown. Further meaningful problem worth of studying is the same attitude control problem without angular velocity measurement and finite-time formation control for multi rigid spacecrafts.
Appendix
Proof of Theorem 1.Suppose the system is finite-time strictly passive and let $V(x)$ be its storage function with
| $u=0.$ |
We get
| $\dot{V}<-cV^{\alpha}<0.$ | (A1) |
Now we will use the inequality to show that $V(x)$ is positive definite. Suppose the equation $\dot{x}=f(x,0)$ has a solution $\varphi(t,x)$,starting from $x$ at $t=0$ and defined on some interval $[0,\delta]$. Integrating (A1) yields
| $V(\varphi(\tau;x))-V(x)\leq-\int_{0}^{\tau}cV^{\alpha}{\rm d}t,\quad \forall\tau\in[0,\delta].$ |
Using
| $V(\varphi(\tau,x))\geq0,$ |
we obtain
| $V(x)\geq\int_{0}^{\tau}cV^{\alpha}{\rm d}t.$ | (A2) |
Suppose that there is $\bar{x}\not=0$ such that $V(\bar{x})=0$. Then (A2) goes to
| $\int_{0}^{\tau}\psi(\varphi(\tau;x)){\rm d}t=0,\quad \forall\tau\in[0,\delta].$ |
Then
| $\varphi(\tau;\bar{x})=0\Rightarrow\bar{x}=0,$ |
which contradicts the claim that
| $\bar{x}\not=0.$ |
This qualifies $V(x)$ as a Lyapunov function candidate,and since
| $\dot{V}<-cV^{\alpha}.$ |
for some $c>0$ and $\alpha\in(0,1)$,we conclude that the origin is finite-time stable.
| [1] | Akella M R. Rigid body attitude tracking without angular velocity feedback. System and Control Letter, 2001, 42(4):321-326 |
| [2] | Luo W, Chu Y, Ling K V. Inverse optimal adaptive control for attitude tracking of spacecraft. IEEE Transactions on Automatic Control, 2005, 50(11):1639-1654 |
| [3] | Mayhew C G, Sanfelice R G, Teel A R. Quaternion-based hybrid control for robust global attitude tracking. IEEE Transactions on Automatic Control, 2011, 56(11):2555-2566 |
| [4] | Schlanbusch R, Loria A, Kristiansen R, Nicklasson P J. PD+ based output feedback attitude control of rigid bodies. IEEE Transactions on Automatic Control, 2012, 57(8):2146-2152 |
| [5] | Crouch P E. Spacecraft attitude control and stabilization:applications of geometric control theory to rigid body models. IEEE Transactions on Automatic Control, 1984, 29(4):321-331 |
| [6] | Wen J T, Kenneth K D. The attitude control problem. IEEE Transactions on Automatic Control, 1991, 36(10):1148-1162 |
| [7] | Egeland O, Godhavn J M. Passivity-based adaptive attitude control of a rigid spacecraft. IEEE Transactions on Automatic Control, 1994, 39(10):842-846 |
| [8] | Yu S H, Yu X H, Shirinzadeh B, Meng Z H. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica, 2005, 41(11):1957-1964 |
| [9] | Jin E, Zhao S. Robust controllers design with finite time convergence for rigid spacecraft attitude tracking control. Aerospace Science Technology, 2008, 12(4):324-330 |
| [10] | Du H, Li S, Qian C. Finite-time attitude tracking control of spacecraft with application to attitude synchronization. IEEE Transactions on Automatic Control, 2011, 56(11):2711-2717 |
| [11] | Meng Z Y, Ren W, You Z. Distributed finite-time attitude containment control for multiple rigid bodies. Automatica, 2010, 46(12):2092-2099 |
| [12] | Scharf D P, Hadeagh F Y, Ploen S R. A survey of spacecraft formation flying guidance and control (Part II):Control. In:Proceedings of the 2004 American Control Conference. Boston, USA:IEEE, 2004. 2976-2985 |
| [13] | Lizarralde F,Wen J T. Attitude control without angular velocity measurement:a passivity approach. IEEE Transactions on Automatic Control, 1996, 41(3):468-472 |
| [14] | Tsiotras P. Stabilization and optimality results for the attitude control problem. Journal of Guidance, Control, and Dynamics, 1996, 19(4):772-779 |
| [15] | Tsiotras P. Further passivity results for the attitude control problem. IEEE Transactions on Automatic Control, 1998, 43(11):1597-1600 |
| [16] | Tayebi A. Unit quaternion based output feedback for the attitude tracking problem. IEEE Transactions on Automatic Control, 2008, 53(6):1516-1520 |
| [17] | Ren W. Distributed cooperative attitude synchronization and tracking for multiple rigid bodies. IEEE Transactions on Control Systems Technology, 2010, 18(2):383-392 |
| [18] | Shuster M D. Survey of attitude representations. The Journal of the Astronautical Science, 1993, 41(4):439-517 |
| [19] | Khalil H K. Nonlinear Systems (Third Edition). Jersey:Prentice Hall, 2002. |
| [20] | Bhat S, Bernstein D. Finite-time stability of continuous autonomous systems. SIAM Journal on Control and Optimization, 2000, 38(3):751-766 |
| [21] | Hardy G, Littlewood J, Polya G. Inequalities. Cambridge, UK:Cambridge University Press, 1952. |
 2015, Vol.2
2015, Vol.2 


