2. School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
Recently,the research of air-breathing hypersonic vehicles (AHVs) has been an interesting issue with great practical value. It is considered as a promising transportation equipment for access to space. However,it is a very challenging problem to design the controller for AHVs as unmanageable nonlinear dynamics including the integrated airframe-propulsion,the uncertainty of atmospheric conditions, the variation of physical and aerodynamic parameters and so on[1, 2, 3, 4].
Due to complex dynamics of AHVs,it is difficult to obtain the real physical mode. Therefore,most research work is based on significative simplified models. For the tracking control of AHVs in cruise phase,it mainly focuses on velocity and attitude control, where main concerns are longitudinal dynamics of AHVs and lateral movements are allowed for further curtailment. Effective controllers have been developed based on linear models at fixed points and nonlinear models in previous work. Gregory et al. used $H_\infty$ and $\mu$ synthesis to a uncertain linear AHV model[5]. Lind proposed the linear parameter-varying method to model and control flexible aircrafts[6]. Oppenheimer et al. developed a modified dynamic inversion controller for the linear time-invariant, unstable,non-minimum phase model of AHVs[7]. Sigthorsson et al. proposed robust linear output feedback control for AHVs. The control methods based on linear models offer simple and efficient ways to locally stabilize dynamical processes of AHVs[3]. Nonlinear models are generally more accurate approximation of AHVs$'$ physical models. Control strategies based on nonlinear models have been proposed for the study of flight control,including adaptive control,robust control,$H_{\infty}$ control,sliding mode control,fuzzy logic control. Gibson et al. adopted the adaptive control for thrust and actuator uncertainties of AHVs[8]. Serrani et al. introduced integrated adaptive guidance and control for constrained nonlinear AHV models[9]. Wang et al. proposed the stochastic robust flight control based on dynamical inversion[10]. Xu et al. provided the adaptive sliding mode control for the cruising control of the AHV with parameter uncertainties[11]. Bowcutt adopted the multidisciplinary optimization control for AHVs[12],and intelligent control algorithms were used by Jiang et al.[13, 14]. These nonlinear controllers on nonlinear vehicle models improve the control performance of AHVs from different aspects.
Sliding mode control (SMC) is one of well-known non-smooth methods,which provides an effective and systematic approach to maintain the consistent stability with good robustness. Therefore, the method is widely accepted in the field of flight control for its robustness. Xu et al. have designed adaptive sliding mode controller for rigid and flexible AHVs,which has shown good insensitivity to uncertainties[11, 15]. In general, non-smooth control laws can improve robustness[16],whereas smooth control laws may not improve disturbance rejection due to Lipschitz continuity of closed loop systems. In sliding mode control,robustness is derived from the discontinuous sign function,which simultaneously leads to the fatal chattering of the traditional sliding mode control. In the practical implementation,actuators can not bear such high frequency switchings. One famous solution to obtain continuous controllers is to introduce boundary layers around sliding mode surfaces proposed by Slotine et al.[17, 18],which provides an asymptotic stability to a preestablished fixed region of the origin.
In this paper,the continuous sliding mode controller is designed to solve the tracking problem of AHVs,which involves continuous terms instead of sign functions in the traditional sliding mode control. In order to keep good robustness,the finite time observer is used to reject disturbances. Before observation errors disappear,system states arrive at small regions around sliding mode surfaces,whose scopes are related to observation errors. When observation errors converge to zero,system states reach sliding mode surfaces and then move to the origin. It means system states can asymptotically converge to the origin with continuous control laws even disturbances exist. Whereas,the boundary layer method can only guarantee the convergence to a fixed neighborhood of the origin.
This paper is organized as follows. In Section II,the preliminary system description and the control-oriented model are provided. In Section III,main results are stated and continuous control laws for velocity and altitude tracking of AHVs are designed. Simulation results are presented in Section IV to illustrate that the proposed method is effective and robust. Conclusion is given in the last section.
Ⅱ. PROBLEM FORMULATION A. The Longitudinal Model of Hypersonic VehiclesOne of the most popular nonlinear models is reported inmost papers[10, 19, 20, 21, 22, 23],which is the longitudinal model of a winged-cone AHV. Bolender et al. proposed to attach elastic characteristics of AHVs to the above longitudinal model for the study of reentry flight[24]. In this paper,the classical nonlinear model derived from NASA Langley Research Center is studied at the trim cruise condition[25]. The flexible mode and the coupling between longitudinal and lateral dynamics are curtailed.
The control-oriented model for longitudinal dynamics are described by five first order differential equations:
| $ \begin{align} \left\{\begin{array}{*{20}lllll} \dot{v}=\frac{T \cos \alpha-D}{m}-\frac{\mu \sin \gamma}{R^{2}},\\ \dot{\gamma}=\frac{L+T \sin \alpha}{mv}-\frac{(\mu-v^{2}R)\cos \gamma}{vR^{2}},\\ \dot{h}=v \sin \gamma,\\ \dot{\alpha}=q-\dot{\gamma},\\ \dot{q}=\frac{M_{yy}}{I_{yy}}, \end{array}\right. \end{align} $ | (1) |
where $v$,$\gamma$,$h$,$\alpha$ and $q$ represent velocity, flight-path angle,altitude,angle of attack and pitch rate, $R=h+R_{E}$ is the altitude of vehicle,$R_{E}$ is the radius of the Earth. $I_{yy}$ is moment of inertia. Left $L$ and draft $D$ are expressed as follows:
| $ \begin{cases} L=\frac{1}{2}\rho v^{2}S C_{L},\\ D=\frac{1}{2}\rho v^{2}S C_{D},\\ C_{L}=0.6203\alpha,\\ C_{D}=0.6450\alpha^{2}+0.0043378\alpha+0.003772. \end{cases} $ |
Pitching moment $M_{yy}$ is described by
| $ \begin{align} \begin{cases} M_{yy}=\frac{1}{2}\rho v^{2}S\bar{c}[C_{M}(\alpha)+C_{M}(\delta_{e})+C_{M}(q)],\\ C_{M}(\alpha)=-0.035\alpha^{2}+0.036616\alpha+5.3261\times 10^{-6},\\ C_{M}(\delta_{e})=c_e(\delta_{e}+d_2(t)-\alpha),\\ C_{M}(q)=\frac{\bar{c}}{2v}q(-6.796\alpha^{2}+0.3015\alpha-0.2289). \end{cases} \end{align} $ |
Thrust $T$ is defined as
| $ \begin{align} \begin{cases} T=\frac{1}{2}\rho v^{2}S C_{T},\\ C_{T}=\begin{cases} 0.02576 \beta,\quad \text{if} ~\beta < 1,\\ 0.02240+ 0.00336 \beta,\quad \text{if} ~\beta \geq 1 \end{cases}\\ \end{cases} \end{align} $ |
The system in (1) is linearized with the given cursing condition $Ma=15$,$v=15\,060$ ${\rm ft/s}$,$h=110\,000$ ft, $\gamma=0^{\mathrm{o}}$,$q=0^{\mathrm{o}}$. The open-loop eigenvalues shown in Fig. 1 are $-0.895$,$0.784$,$-0.00021 \pm 0.0362{\rm j}$ and 0.00011[26],where -0.895 and 0.784 are the short period oscillation,corresponding to q and $\alpha$,$-0.00021 \pm 0.0362{\rm j}$ are the phugoid w.r.t. $v$ and $\gamma$,0.00011 is the eigenvalue about the altitude modal. It is obvious the nonlinear aircraft in (1) is unstable.
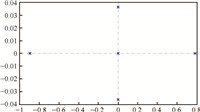
|
Download:
|
| Fig. 1. The open-loop eigenvalues of winged-cone model at the given cursing condition. | |
The engine dynamic of the aircraft is expressed by a second order differential equation with the control input $\beta_c$
| $ \begin{align} \ddot{\beta}=-2\xi w_{n}\dot{\beta}-w_{n}^{2}\beta+w_{n}^{2}(\beta_{c}+d_1(t)). \end{align} $ | (2) |
The precise definition of every variable in the equations (1) and (2) is stated in Appendix A.
The composite controlled system contains the equations (1) and (2). The elevator deflection angle $\delta_e$ and the demand of the engine control input $\beta_c$ are the control inputs,and the longitudinal velocity $v$ and the altitude $h$ are outputs. Considering the equations (1) and (2),$v$ has the relation with $\beta_c$ and $\delta_e$,which is derived as
| $ \begin{align} &\dot{v} \propto \beta,\dddot{v} \propto \ddot{\beta}, \dddot{v} \propto \beta_c,\end{align} $ | (3) |
| $ \begin{align} &\dot{v} \propto \cos \alpha,\dddot{v} \frac{1}{\propto} \ddot{\alpha},\dddot{v} \frac{1}{\propto} \dot{q},\dddot{v} \frac{1}{\propto} M_{yy},\dddot{v} \frac{1}{\propto} \delta_e. \end{align} $ | (4) |
Similarly,the relationship is investigated among $h$,$\beta_c$ and $\delta_e$. As
| $ \begin{align} \dot{h} \propto v, \end{align} $ | (5) |
then we have
| $ \begin{align} h^{(4)} \propto \beta_c,h^{(4)} \frac{1}{\propto} \delta_e. \end{align} $ | (6) |
Therefore,$\beta_c$ and $\delta_e$ are explicitly contained in $\dddot{v}$ and $h^{(4)}$.
The aircraft in (1) and (2) can be included by the general nonlinear formula,
| $ \begin{align} \left\{\begin{array}{*{20}lllll} \dot{x}=f(x)+\sum^{m}\limits_{i=1}b_i(x)u_i(t),\\ y=\vartheta(x), \end{array}\right. \end{align} $ | (7) |
where $x\in {\bf R}^n$ is the state vector,$u(t),\vartheta(x) \in {\bf R}^m $ are inputs and outputs. $f(x)$ and $b_{i}(x)$ along with the function $\vartheta_{i}$ are smooth functions on ${\bf R}^{n}$,allowing arbitrary order derivatives to be calculated.
As the system in (7) has $m$ output components,it is considered to produce $m$ subsystems if the input-output feedback linearization is executed,where the relative degree of the $i$-th subsystem is recorded as $r_i$,$i=1,\cdots,m$.
Assumption 1. All the relative degree $r_i,i=1,\cdots,m$ of $m$ subsystems are constant and known. The system in (7) does not contain zero dynamics,which means that the system degree $\tilde{r}$ is equal to the sum of relative degrees $r_i$, $\tilde{r}=\sum^{m}_{i=1} r_{i}$.
The $r_i$-th derivative of $y_i=\vartheta_{i}(x)$ can be expressed by Lie derivatives
| $ \begin{align} y^{(r_i)}_{i}=L^{r_i}_{f}\vartheta_{i}(x)+\sum^m_{i=1}L_{b_{i}}(L^{r_{i}-1}_{f}\vartheta_{i}(x) )u_i, \end{align} $ | (8) |
where $L_{f}\vartheta_{i}(x)$ is the Lie derivative of the function $\vartheta_{i}$ along the vector field $f$,
| $ \begin{align} &L_{f}\vartheta_{i}(x)=\frac{\partial \vartheta_{i}(x)}{\partial x}f(x)= \\ &\quad\qquad\frac{\partial \vartheta_{i}(x)}{\partial x_1}f_1(x)+\cdots+\frac{\partial \vartheta_{i}(x)}{\partial x_n}f_n(x), \end{align} $ |
$L_{b_{i}}\vartheta_{i}(x)$ and $L^{r_{i}}_{f}\vartheta_{i}(x)$ are also identically defined by Lie derivatives.
The composite controlled system in (1) and (2) reveals that the system degree is $\tilde{r}=7$. According to (3) and (4),the relative degree of velocity subsystem to inputs is $r_1=3$. The relative degree of altitude subsystem to inputs is $r_2=4$ referring to (6).
It means that the system degree equals to the total relative degrees of subsystems. In other words,the feedback linearization can be executed to reveal that $\dddot{v}$ and $h^{(4)}$ must be explicitly expressed by the control inputs $\delta_e$ and $\beta_c$. The original nonlinear model is transformed into two coupling subsystems from inputs to outputs. Therefore we consider the following two subsystems for the cruising control,
Velocity subsystem:
| $ \begin{align} \left\{\begin{array}{*{20}llllllllll} \dot{\zeta}^{1}_{1}=\dot{v}(x)=L_{f}v(x),\\ \qquad \vdots \\ \dot{\zeta}^{1}_{r_1}=L_{f}^{r_1}v(x)+\Sigma_{i=1}^{r_1-1}L_{b_{i}}(L_{f}^{r_1-1}v(x))u_{i}. \end{array}\right. \end{align} $ | (9) |
Altitude subsystem:
| $ \begin{align} \left\{\begin{array}{*{20}lllllllllll} \dot{\zeta}^{2}_{1}=\dot{h}(x)=L_{f}h(x),\\ \qquad \vdots \\ \dot{\zeta}^{2}_{r_2}=L_{f}^{r_2}h(x)+\Sigma_{i=1}^{r_2-1}L_{b_{i}}L_{f}^{r_2-1}h(x)u_{i}. \end{array}\right. \end{align} $ | (10) |
The $r_i$-th derivatives of velocity and altitude dynamics have the explicit expression with control variables,combining $\dot{\zeta}^{1}_{r_1}$ and $\dot{\zeta}^{2}_{r_2}$ as follows:
| $ \begin{align} \begin{bmatrix} v^{(r_1)}(x) \\ h^{(r_2)}(x) \end{bmatrix}=\begin{bmatrix} L_{f}^{r_1}v(x) \\ L_{f}^{r_2}h(x) \end{bmatrix}+B(x)\begin{bmatrix} \beta_c \\ \delta_e \end{bmatrix}, \end{align} $ | (11) |
where
| $ \begin{align*} B(x)=\begin{bmatrix} L_{b_{1}}L_{f}^{r_1-1}v(x) & L_{b_{2}}L_{f}^{r_1-1}v(x) \\ L_{b_{1}}L_{f}^{r_2-1}h(x) & L_{b_{2}}L_{f}^{r_2-1}h(x) \end{bmatrix}, \end{align*} $ |
is nonsingular over the entire flight envelope given in [19, 20]. As $r_1=3$ and $r_2=4$,the derivatives of $v$ and $h$ are calculated by the chain rule,
| $ \begin{align} &\dot{v}=f_1(x),\\ &\ddot{v}=\frac{1}{m}\tilde{w}\dot{x},\\ &\dddot{v}=L_{f}^{(3)}v(x) + \begin{bmatrix} L_{b_{1}}L_{f}^{2}v(x) & L_{b_{2}}L_{f}^{2}v(x) \end{bmatrix} u ,\\ &L_{f}^{(3)}v(x)=\frac{1}{m}(\tilde{w}\ddot{x}_{0}+\dot{x}^{\mathrm{T}}\Omega\dot{x}),\\ &L_{b_{1}}L_{f}^{2}v(x) =\frac{\rho v^{2}Sc_{\beta}w_{n}^{2}}{2m}\cos\alpha ,\\ &L_{b_{2}}L_{f}^{2}v(x)=-\frac{c_{e}\rho v^{2}S\bar{c}}{2mI_{yy}}(T\sin\alpha+D_{\alpha}),\\ &\dot{h}= f_3(x),\\ &\ddot{h}=\dot{v} \sin \gamma+v \dot{\gamma}\cos \gamma,\\ &h^{(3)}=\ddot{v} \sin \gamma+2\dot{v} \dot{\gamma}\cos \gamma-v \dot{\gamma}^{2} \sin \gamma+v \ddot{\gamma}\cos\gamma ,\\ &h^{(4)}=L_{f}^{(4)}h(x)+\begin {bmatrix} L_{b_{1}}L_{f}^{3}h(x) & L_{b_{2}}L_{f}^{3}h(x) \end{bmatrix} u ,\\ &L_{f}^{(4)}h(x)=(3\ddot{v} \dot{\gamma}+3\dot{v} \ddot{\gamma})\cos \gamma+ \frac{\sin \gamma}{m}(\tilde{w}\ddot{x}_{0}+\dot{x}^{\mathrm{T}}\Omega\dot{x}),\\ &L_{b_{1}}L_{f}^{3}h(x)=\frac{\rho v^{2}Sc_{\beta}w_{n}^{2}}{2m}\sin(\alpha+\gamma),\\ & L_{b_{2}}L_{f}^{3}h(x)=\frac{c_{e}\rho v^{2} S \bar{c} }{2mI_{yy}}[T\cos(\alpha+\gamma)+L_{\alpha}\cos\gamma-D_{\alpha}\sin\gamma]. \end{align} $ |
The expressions of $\dot{x}$,$\ddot{x}$,$\ddot{x}_{0}$, $\ddot{\alpha}_{0}$,$\ddot{\beta}_{0}$,$\ddot{\gamma}$, $\dddot{\gamma}$,$\tilde{w}$,$\Omega$,$\tilde{\pi}$ and $\Pi$ refer to Appendix A[10].
Remark 1. The feedback linearization transformation aims to explore the explicit control inputs for the outputs of velocity and altitude,which provides the control-oriented subsystems. However,as $L_{f}^{3}v(x)$,$L_{f}^{4}h(x)$ and $B(x)$ are nonlinear,the two subsystems are still nonlinear and coupled. It is easier to design the controller with the explicit control inputs than that with implicit inputs.
According to the formulae of (9) and (10),the general model of subsystems is described as follows,
| $ \begin{align} \left\{\begin{array}{*{20}lllllllllll} \dot{\sigma}_{j}=\sigma_{j+1},\\ \dot{\sigma}_{r_i}=\bar{f}_i(x)+\bar{b}_i(x)u(t). \end{array}\right. \end{align} $ | (12) |
As external disturbances $d_1(t)$ and $d_2(t)$ existing in $\ddot{\beta}$ and $C_{M}(\delta_{e})$ are considered to be matched,the $r_i$-th subsystem is concluded to the manifold,
| $ \begin{align} \left\{\begin{array}{*{20}lll} \dot{\sigma}_{j}=\sigma_{j+1},\\ \dot{\sigma}_{r_i}=\bar{f}_i(x)+\bar{b}_i(x)(u(t)+d(t)), \end{array}\right. \end{align} $ | (13) |
where $i=1,2$,$j=1,2,\cdots,r_i-1$, $\bar{f}_i(x)=L_{f}^{r_i}\vartheta_i(x)$, $\bar{b}_i(x)=[L_{b_{1}}(L_{f}^{r_i-1}\vartheta_i),L_{b_{2}}(L_{f}^{r_i-1}\vartheta_i)]$, $d(t)=[d_1(t),d_2(t)]^{\mathrm{T}}$,$u(t)=[\beta_c, \delta_e]^{\mathrm{T}}$.
Control object: In this paper,the objective is to design a robust continuous sliding mode controller based on velocity and altitude subsystems in the manifold (13),such that the velocity $v$ and the altitude $h$ can track their reference $v_r$ and $h_r$, especially existing unknown external disturbances.
Ⅲ. CONTINUOUS SLIDING MODE CONTROLLER DESIGN WITH DISTURBANCE COMPENSATION FOR AIR-BREATHING HYPERSONIC VEHICLESIn this section,the continuous sliding mode controller is studied for the tracking control. When disturbances exist,the original feedback control law is applied to (11),
| $ \begin{align} u=\bar{b}^{-1}(x)(-\bar{f}(x)+w), \end{align} $ | (14) |
where $\bar{f}(x)=[\bar{f}_1(x),\bar{f}_2(x)]^{\mathrm{T}}$, $\bar{b}(x)=[\bar{b}_1(x),\bar{b}_2(x)]^{\mathrm{T}}$,$w=[w_1, w_2]^{\mathrm{T}}$ is the auxiliary control vector. In this case, the controlled objective (13) is equivalent to the $r_i$-th order integrator system,
| $ \begin{align} \left\{\begin{array}{*{20}lll} \dot{\sigma}_{j}=\sigma_{j+1},\\ \dot{\sigma}_{r_i}=w_{i}+\bar{d}_i(t), \end{array}\right. \end{align} $ | (15) |
where $\bar{d}_i(t)=\bar{b}_i(x)*d(t)$,$i=1,2$, $j=1,2,\cdots,r_i-1$.
A. Disturbance Observer DesignThe purpose of disturbance observer is to efficiently estimate real-time disturbances. Observed values are used as compensation terms included in control signals. With the compensator, disturbances can be restrained to zero after a finite time,and the controller guarantees the accessibility and the stability before the free-error observation is achieved.
Considering the tracking problem of AHVs,it is presented as
| $ \begin{align} \left\{\begin{array}{*{20}llll} \dot{\sigma}_{r_{1}}(x)=\bar{f}_1(x) + \bar{b}_1(x) u(t)+ \bar{d}_1(t)\\ \dot{\sigma}_{r_{2}}(x)=\bar{f}_2(x) + \bar{b}_2(x) u(t)+ \bar{d}_2(t) \end{array}\right. \end{align} $ | (16) |
As
| $ \begin{align} & \dot{\sigma}_{r}=[\dot{\sigma}_{r_{1}}(x),\dot{\sigma}_{r_{2}}(x)]^\mathrm{T},\\ & w=[w_1,w_2]^{\mathrm{T}}=[\bar{f}_1(x)+\bar{b}_1(x)u(t),\bar{f}_2(x)+\bar{b}_2(x)u(t)]^\mathrm{T},\\ & \bar{f}_1(x)=L_{f}^{3}v(x),\bar{f}_2(x)=L_{f}^{4}h(x),\\ & \bar{b}_1(x)=[L_{b_{1}}(L_{f}^{2}v(x)),L_{b_{2}}(L_{f}^{2}v(x))],\\ & \bar{b}_2(x)=[L_{b_{1}}(L_{f}^{3}h(x)),L_{b_{2}}(L_{f}^{3}h(x))],\\ & u(t)=[u_1(t),u_2(t)]^\mathrm{T},\\ &\bar{d}(t)=[\bar{d}_1(t),\bar{d}_2(t)]^{\rm T}=[\bar{b}_1(x)d_1(t),\bar{b}_2(x) d_2(t)]^\mathrm{T}. \end{align} $ |
For the differential equation (16),where $\sigma_{r}$ is continuous vector function,the disturbance vector $\bar{d}(t)$ is bounded and has Lipshitz constants $L=[L_1,L_2]^\mathrm{T}$,where $|\bar{d}_1(t)|\leq L_1 $ and $|\bar{d}_2(t)|\leq L_2$. Therefore, second order observers are used to observe $\bar{d}_1(t)$ and $\bar{d}_2(t)$ referring to Appendix B,which are expressed in the form of vectors as follows:
| $ \begin{align} \left\{\begin{array}{*{20}llll} \dot{z}_0=\nu_0+ w,\\ \nu_0=- \lambda_0 L ^{ \frac{1}{3} } |z_0 - \sigma_{r} | ^{ \frac{2}{3} }\textrm{sgn} (z_0 - \sigma_{r}) + z_1,\\ \dot{z}_1=\nu_1,\\ \nu_1=- \lambda_1 L ^{ \frac{1}{2} } | z_1 - \nu_0 |^{ \frac{1}{2} } \textrm{sgn} ( z_1 - \nu_0 ) + z_2,\\ \dot{z}_{2}= - \lambda_{2} L \textrm{sgn} ( z_{2} - \nu_{1} ), \end{array}\right. \end{align} $ | (16) |
where $\lambda_0$,$\lambda_1$,$\lambda_2$ are gains of the observer,$L ^{ \frac{1}{p} }=[L^{ \frac{1}{p}}_1,L^{ \frac{1}{p}}_2]^\mathrm{T}$,$z_i=[z^1_i,z^2_i]^\mathrm{T}$. $z_1(t)$ converges to $\bar{d}(t)$ in finite time.
Remark 2. The convergence proof of disturbance observer can refer to literatures[27, 28]. In addition,the $l$-th order observer provides more accurate derivatives than the $p$ order observer,$p \leq l$[29]. By (17),$z_1$ can converge to $\bar{d}(t)$ in finite time,which guarantees that observation errors converge to zero in finite time.
B. Continuous Sliding Mode Controller DesignFor the subsystem expressed in (15),define $\sigma=[\sigma_1, \sigma_2,\cdots,\sigma_{r_i}]^{\mathrm{T}}$,the sliding surface is as follows:
| $ \begin{align} s_{r_i}(\sigma,t)=(\frac{\textrm{d}}{\textrm{d} t}+\lambda)^{r_i-1}\sigma_1 = C \sigma^{\mathrm{T}}, \end{align} $ | (17) |
where $C=[c^{r_i-1}_{r_i-1}\lambda^{r_i-1},\cdots, c^{1}_{r_i-1}\lambda,c^{0}_{r_i-1}]$, $c^{q}_{r_i-1}=\frac{(r_i-1)!}{(r_i-q-1)!q!}$, $q=0,1,\cdots,r_i-1$. The time derivative of sliding mode surface is given as
| $ \begin{align} \dot{s}_{r_i}(\sigma,t)= \dot{\sigma}_{r_i} + \bar{C} \sigma^{\mathrm{T}}, \end{align} $ | (18) |
where $\bar{C}=[0,c^{r_i-1}_{r_i-1}\lambda^{r_i-1},\cdots, c^{1}_{r_i-1}\lambda]$. If the derivative is designed as
| $ \begin{align} \dot{s}_{r_i}(\sigma,t)=e_{d_i}(t)- \ell_1 \textrm{sig}^{o_1}(s_{r_i})- \ell_2 \textrm{sig}^{o_2}(s_{r_i}), \end{align} $ | (19) |
where $e_{d_i}(t)=\bar{d}_i(t)-z^i_1(t)$,$\ell_{1}>0$, $\ell_{2}>0$,$0 < o_1 < 1$,$o_2>1$, $\textrm{sig}^{o_i}(s_{r_i})=|s_{r_i}|^{o_i}\textrm{sgn}(s_{r_i})$. We can get the following theorem.
Theorem 1. For system (15),if the continuous controller is used
| $ \begin{align} w_i=-\bar{C} \sigma^{\mathrm{T}}-z^i_1(t)- \ell_1 \textrm{sig}^{o_1}(s_{r_i})- \ell_2 \textrm{sig}^{o_2}(s_{r_i}), \end{align} $ | (20) |
the reachability of $s_{r_i}$ has two cases:
1) if the observer error $e_{d_i}(t)=0$,system states reach the sliding manifold $s_{r_i}=0$ in finite time;
2) if the observer error $ e_{d_i}(t) \neq 0$,system states reach the $\psi$ neighborhood of $s_{r_i}=0$ in finite time and never escape from the region,where $ | s_{r_i} | \leq \psi=\min \{\psi_1,\psi_2 \} $, $\psi_1=|\frac{e_{d_i}(t)}{\ell_1}|^{\frac{1}{o_1}}$ and $\psi_2=|\frac{e_{d_i}(t)}{\ell_2}|^{\frac{1}{o_2}}$.
Proof. The Lyapunov function is selected as $V_1=\frac{1}{2}s_{r_i}^{2}$,where $V_1$ is positive definite.
Case 1: $e_{d_i}(t)=0$,the time derivative of $V_1$
| $ \begin{align} &\dot{V}_1=s_{r_i}^{T}\dot{s}_{r_i}= \\ &\qquad s^{T}_{r_i}(e_{d_i}(t)-\ell_{1}|s_{r_i}|^{o_1}\textrm{sgn}(s_{r_i})- \ell_{2} |s_{r_i}|^{o_2}\textrm{sgn}(s_{r_i}))= \\ &\qquad -\ell_{1}|s_{r_i}|^{1+o_1}-\ell_{2} |s_{r_i}|^{1+o_2}= \\ &\qquad -2^{\frac{1+o_1}{2}}\ell_{1}V^{\frac{1+o_1}{2}}_1- 2^{\frac{1+o_2}{2}}\ell_{2}V^{\frac{1+o_2}{2}}_1 \leq \\ &\qquad - 2^{\frac{1+o_1}{2}} \ell_{1} V^{\frac{1+o_1}{2}}_1. \end{align} $ | (21) |
As $0 < o_1 < 1$,$\frac{1}{2} < \frac{1+o_1}{2} < 1$,$\dot{V}_1 \leq - 2^{\frac{1+o_1}{2}} \ell_{1} V^{\frac{1+o_1}{2}}_1$ implies that system states reach the sliding manifold $s=0$ within the finite time $T \leq \frac{1}{\ell_1(1-o_1)}2^{\frac{1-o_1}{2}}|V_1(s_{r_i}(t_0))|^{\frac{1-o_1}{2}}$.
Case 2: $e_{d_i}(t)\neq 0$,
| $ \begin{align} \dot{V}_1=s_{r_i}^{T}[e_{d_i}(t)-\ell_{1}|s_{r_i}|^{o_1}\textrm{sgn}(s_{r_i})-\ell_{2} |s_{r_i}|^{o_2}\textrm{sgn}(s_{r_i})]. \notag \end{align} $ |
The time derivative of $V_1$ can be reformulated in two forms. One form is
| $ \begin{align} \begin{split} \dot{V}_1= s_{r_i}^{T} [&-(\ell_{1}-e_{d_i}(t)(|s_{r_i}|^{o_1}\textrm{sgn}(s_{r_i}))^{-1})| s_{r_i}|^{o_1}\textrm{sgn}(s_{r_i}) \\ &-\ell_{2} |s_{r_i}|^{o_2}\textrm{sgn}(s_{r_i})]. \end{split} \end{align} $ |
The other form is
| $ \begin{align} \begin{split} \dot{V}_1= s^{T}_{r_i}[&-(\ell_{2}- e_{d_i}(t)(|s_{r_i}|^{o_2}\textrm{sgn}(s_{r_i}))^{-1})| s_{r_i}|^{o_2}\textrm{sgn}(s_{r_i}) \\ &-\ell_{1}|s_{r_i}|^{o_1}\textrm{sgn}(s_{r_i})]. \end{split} \end{align} $ |
If $(\ell_{1}-e_{d_i}(t)(|s_{r_i}|^{o_1}\textrm{sgn}(s_{r_i}))^{-1})$ is positive definite,or if $(\ell_{2}-e_{d_i}(t)(|s_{r_i}|^{o_2}\textrm{sgn}(s_{r_i}))^{-1})$ is positive definite,then $\dot{V}_1$ has the form of $\dot{V}_1=-s^{T}_{r_i}(\bar{\ell}_{1}|s_{r_i}|^{o_1}\textrm{sgn}(s_{r_i})+ \bar{\ell}_{2}|s_{r_i}|^{o_2}\textrm{sgn}(s_{r_i}))$, where $\bar{\ell}_{1}>0$,$\bar{\ell}_{2}>0$,which still guarantee the finite time reachability. By the above analysis, solve $\psi_1=|\frac{e_{d_i}(t)}{\ell_1}| ^{\frac{1}{o_1}}$ and $\psi_2=|\frac{e_{d_i}(t)}{\ell_2}|^{\frac{1}{o_2}}$.
If $|s_{r_i}| > \psi=\min\{ \psi_1,\psi_2\}$, $(\ell_{1}-e_{d_i}(t)(|s_{r_i}|^{o_1}\textrm{sgn}(s_{r_i}))^{-1})$ and $(\ell_{2}-e_{d_i}(t)(|s_{r_i}|^{o_2}\textrm{sgn}(s_{r_i}))^{-1})$ are both positive definite,the system states reach the region $|s_{r_i}| > \psi$ in finite time.
When $|s_{r_i}|=\psi= \min\{ \psi_1,\psi_2\}$,one case is $|s_{r_i}| =\psi_1$,which makes
| $ \begin{align} &\dot{V}_1=s_{r_i}^{T}(-\ell_{2} |s_{r_i}|^{o_2}\textrm{sgn}(s_{r_i}))=-\ell_{2} \psi^{1+o_2}_1 =\notag\\ &\qquad -\ell_{2}\ell^{-\frac{1+o_2}{o_1}}_{1}|e_{d_i}(t)| ^{\frac{1+o_2}{o_1}}. \end{align} $ | (22) |
The other case is $|s_{r_i}|=\psi_2$,
| $ \begin{align} &\dot{V}_1 =s^{T}_{r_i}(-\ell_{1}|s_{r_i}|^{o_1}\textrm{sgn}(s_{r_i}))=-\ell_{1}\psi^{1+o_1}_2 = \notag\\ &\qquad -\ell_{1}\ell^{-\frac{1+o_1}{o_2}}_{2} |e_{d_i}(t)| ^{\frac{1+o_1}{o_2}}. \end{align} $ | (23) |
From the two cases,it can be concluded that the system states can reach the surface $|s_{r_i}|=\psi$ in finite time.
The region $|s_{r_i}| \leq \psi=\min\{ \psi_1,\psi_2\}$ is an attractive area for the states of system (15). System states do not escape from the region once reach it. To prove that,we need only to show that any system state on the boundary $|s_{r_i}|=\psi = \min\{ \psi_1,\psi_2\}$,never enters the region of $|s_{r_i}|> \psi=\min\{ \psi_1,\psi_2\}$ again. According to the above analysis,the time derivative of $V_1(s_{r_i})$ on the boundary $|s_{r_i}|= \min\{ \psi_1,\psi_2\}$ is always negative definite refereing to (22) and (23),namely $\dot{V}_1(s_{r_i})=- \ell$, $\ell>0$. This means $|s_{r_i}|$ is monotonically decreasing, system states on the boundary enter the region $|s_{r_i}| < \psi$ and never escape it.
In sum,with the controller (21),the states of system (15) always reach the sliding mode surface $s_{r_i}=0$ in finite time without observation errors and arrive at the region $|s_{r_i}| \leq \psi$ in finite time if observation errors exist.
C. Continuous Sliding Mode Controller with Disturbance Compensation for The Tracking Control of AHVsDefine the tracking error as $e_{v}(t)=v(t)-v_{r}(t)$ and $e_{h}(t)=h(t)-h_{r}(t)$,such that
| $ \begin{align} \left\{\begin{array}{*{20}ll} \dot{e}_{v}=\dot{v}-\dot{v}_{r},\\ \ddot{e}_{v}=\ddot{v}-\ddot{v}_{r},\\ \dddot{e}_{v}=\bar{f}_1(x)+\bar{b}_1(x)u(t)+\bar{d}_1(t)-\dddot{v}_{r}, \end{array}\right. \end{align} $ | (24) |
and
| $ \begin{align} \left\{\begin{array}{*{20}ll} \dot{e}_{h}=\dot{h}-\dot{h}_{r},\\ \ddot{e}_{h}=\ddot{h}-\ddot{h}_{r},\\ \dddot{e}_{h}=\dddot{h}-\dddot{h}_{r},\\ {e}^{(4)}_{h}=\bar{f}_2(x)+\bar{b}_2(x)u(t)+\bar{d}_2(t)-h^{(4)}_{r}. \end{array}\right. \end{align} $ | (25) |
For disturbances $\bar{d}_1(t)$ and $\bar{d}_2(t)$,the disturbance observer is used to estimate them. We have the corollary for observation errors.
Corollary 1. The disturbance observation errors, $e_{d_i}(t)= \bar{d}_i(t)-{z}^i_1(t)$,$i=1,2$,are obviously bounded and should converge to zero after a finite time $T$,which is
| $ \begin{align} \|e_{d_i}(t)\| \begin{cases} \leq \tau_i,\quad t < T \\ =0 ,\quad t \geq T \end{cases} \end{align} $ | (26) |
where $ \tau_i,i=1,2$ is bounded constants.
Theorem 2. For system (24) and (25),if the following continuous sliding mode controller with disturbance compensation is used,
| $ \begin{align} \scriptstyle u= \begin{bmatrix} \scriptstyle \bar{b}_{1}(x) \\ \scriptstyle \bar{b}_{2}(x) \end{bmatrix}^{\scriptstyle -1} \begin{bmatrix} \scriptstyle \dddot{v}_r-\bar{f}_{1}(x) -\bar{\lambda}_v E_v -{z}^1_1(t)- \ell_1 \textrm{sig}^{o_1}(s_v) - \ell_2 \textrm{sig}^{o_2}(s_v) \\ \scriptstyle h^{(4)}_r-\bar{f}_{2}(x) -\bar{\lambda}_h E_h -{z}^2_1(t) - \ell_1 \textrm{sig}^{o_1}(s_h) - \ell_2 \textrm{sig}^{o_2}(s_h) \end{bmatrix}, \end{align} $ | (27) |
the velocity $v$ and the altitude $h$ are guaranteed to asymptotically track reference signals $v_r$ and $h_r$ with switching modes $s_v$ and $s_h$,where ${z}^1_1(t)$ and ${z}^2_1(t)$ are compensation terms for disturbances $\bar{d}_1(t)$ and $\bar{d}_2(t)$,respectively,obtained by (17).
Proof. Via feedback linearization,two decoupled subsystems are presented. The velocity switching mode is designed in the manifold,
| $ \begin{align*} \begin{aligned} s_{v}&=(\frac{\textrm{d} }{\textrm{d}t}+ \lambda)^2 e_{v}= \ddot{e}_{v}+ 2 \lambda \dot{e}_{v}+\lambda^2 e_{v}=\lambda_v E_v, \end{aligned} \end{align*} $ |
where $\lambda_v=[c^{2}_{2} \lambda^2,c^{1}_{2} \lambda,1]$, $E_v=[e_v,\dot{e}_v,\ddot{e}_v]^{\mathrm{T}}$. The time derivative of $s_{v}$ is
| $ \begin{align*} \begin{aligned} \dot{s}_{v}&=\dddot{e}_{v}+2 \lambda\ddot{e}_{v}+\lambda^2\dot{e}_{v}= \\ &\dddot{e}_{v}+ \bar{\lambda}_v E_v = \\ &\bar{f}_1(x)+\bar{b}_1(x)u(t)+\bar{d}_1(t)-\dddot{v}_{r}+\bar{\lambda}_v E_v, \end{aligned} \end{align*} $ |
where $\bar{\lambda}_v=[0,c^{2}_{2} \lambda^2,c^{1}_{2} \lambda]$.
The altitude switching mode is considered as
| $ \begin{align*} \begin{aligned} s_{h}&=(\frac{\textrm{d} }{\textrm{d}t}+ \lambda)^3 e_{h}= \dddot{e}_{h}+ 3 \lambda \ddot{e}_{h}+ 3 \lambda^2 \dot{e}_{h} + \lambda^3 e_{h} = \\ &\lambda_h E_h, \end{aligned} \end{align*} $ |
where $\lambda_h=[c^{3}_{3} \lambda^3,c^{2}_{3} \lambda^2,c^{1}_{3} \lambda,1]$, $E_h=[e_h,\dot{e}_h,\ddot{e}_h,\dddot{e}_h]^{\mathrm{T}}$. The time derivative of $s_{h}$ is
| $ \begin{align*} \begin{aligned} \dot{s}_{h}&=e^{(4)}_{h}+ 3 \lambda \dddot{e}_{h}+ 3 \lambda^2 \ddot{e}_{h} + \lambda^3 \dot{e}_{h}= \\ &e^{(4)}_{h}+ \bar{\lambda}_h E_h = \\ &\bar{f}_2(x)+\bar{b}_2(x)u(t)+\bar{d}_2(t)-h^{(4)}_{r}+\bar{\lambda}_h E_h . \end{aligned} \end{align*} $ |
where $\bar{\lambda}_h=[0,c^{3}_{3} \lambda^3,c^{2}_{3} \lambda^2,c^{1}_{3} \lambda]$.
Combining the equations of $\dot{s}_{v}$ and $\dot{s}_{h}$,we have the compact expression
| $ \begin{align*} \begin{aligned} \begin{bmatrix} \scriptstyle \dot{s}_{v} \\ \scriptstyle \dot{s}_{h} \end{bmatrix} \scriptstyle = \begin{bmatrix} \scriptstyle \bar{f}_{1}(x) \\ \scriptstyle \bar{f}_{2}(x) \end{bmatrix} \scriptstyle + \begin{bmatrix} \scriptstyle \bar{b}_{1}(x) \\ \scriptstyle \bar{b}_{2}(x) \end{bmatrix} \begin{bmatrix} \scriptstyle \beta_c\\ \scriptstyle \delta_e \end{bmatrix} \scriptstyle + \begin{bmatrix} \scriptstyle \bar{d}_{1}(t) \\ \scriptstyle \bar{d}_{2}(t) \end{bmatrix} \scriptstyle - \begin{bmatrix} \scriptstyle \dddot{v}_{r} \\ \scriptstyle h^{(4)}_{r} \end{bmatrix} \scriptstyle + \begin{bmatrix} \scriptstyle \bar{\lambda}_v E_v \\ \scriptstyle \bar{\lambda}_h E_h \end{bmatrix}. \end{aligned} \end{align*} $ |
The Lyapunov function is selected as $V_v=\frac{1}{2}s^{\mathrm{T}}_v s_v$, $V_h=\frac{1}{2}s^{\mathrm{T}}_h s_h$,then we have its derivative with the form
| $ \begin{align*} \begin{split} &\begin{bmatrix} \scriptstyle \dot{V}_v \\ \scriptstyle \dot{V}_h \end{bmatrix} = \\ &\quad \begin{bmatrix}\scriptstyle s_v & 0 \\ \scriptstyle 0 & s_h \end{bmatrix} \scriptstyle \biggl ( \begin{bmatrix} \scriptstyle \bar{f}_{1}(x) \\ \scriptstyle \bar{f}_{2}(x) \end{bmatrix} \scriptstyle + \begin{bmatrix} \scriptstyle \bar{b}_{1}(x) \\ \scriptstyle \bar{b}_{2}(x) \end{bmatrix} \begin{bmatrix} \scriptstyle \beta_c\\ \scriptstyle \delta_e \end{bmatrix} \scriptstyle + \begin{bmatrix} \scriptstyle \bar{d}_{1}(t) \\ \scriptstyle \bar{d}_{2}(t) \end{bmatrix} \scriptstyle - \begin{bmatrix} \scriptstyle \dddot{v}_{r} \\ \scriptstyle h^{(4)}_{r} \end{bmatrix} \scriptstyle + \begin{bmatrix} \scriptstyle \bar{\lambda}_v E_v \\ \scriptstyle \bar{\lambda}_h E_h \end{bmatrix} \scriptstyle \biggl ). \end{split} \end{align*} $ |
The control variables in the above formula are replaced by the designed control law (27),then the derivative of $V$ is
| $ \begin{align} \begin{bmatrix} \dot{V}_v \\ \dot{V}_h \end{bmatrix}=\begin{bmatrix} s_v & 0 \\ 0 & s_h \end{bmatrix} \biggl [\begin{matrix} e_{d_1}(t)- \ell_1 \textrm{sig}^{o_1}(s_v) - \ell_2 \textrm{sig}^{o_2}(s_v)\\ e_{d_2}(t)- \ell_1 \textrm{sig}^{o_1}(s_h) - \ell_2 \textrm{sig}^{o_2}(s_h) \end{matrix} \biggl]. \end{align} $ | (28) |
Corollary 1 shows the property of observation errors $e_{d_i}(t)$,which is bounded and converges to zero after a finite time. According to Theorem 2,when $e_{d_i}(t) \neq 0$, system states would reach neighborhoods of switching modes with respect to $e_{d_i}(t)$. When $e_{d_1}(t) \neq 0$,system states $[e_v,\dot{e}_v,\ddot{e}_v]$ reach the $\psi_v$ region of $s_v=0$,$\psi_v= \min \{|\frac{e_{d_1}(t)}{\ell_1}|^{\frac{1}{o_1}}, |\frac{e_{d_1}(t)}{\ell_2}|^{\frac{1}{o_2}} \}$. When $e_{d_2}(t) \neq 0$,system states $[e_h,\dot{e}_h,\ddot{e}_h,\dddot{e}_h]$ reach the $\psi_h$ region of $s_h=0$,$\psi_h= \min \{|\frac{e_{d_2}(t)}{\ell_1}|^{\frac{1}{o_1}}, |\frac{e_{d_2}(t)}{\ell_2}|^{\frac{1}{o_2}} \}$. $e_{d_i}(t)$ eventually stabilizes to zero after a finite time,system states also reach $s_v=0$ and $s_h=0$ in finite time.
When $s_v=0$ and $s_h=0$,the dynamics of tracking error system on sliding modes $s_v=0$ and $s_h=0$ are obtained,
| $ \begin{align*} \begin{split} &\ddot{e}_{v}+2 \lambda \dot{e}_{v}+\lambda^2 e_{v}=0,\\ &\dddot{e}_{h}+ 3 \lambda \ddot{e}_{h}+ 3 \lambda^2 \dot{e}_{h} + \lambda^3 e_{h}=0. \\ \end{split} \end{align*} $ |
It can be concluded that $e_{v}=c_1 {\rm e}^{-\lambda t}$, $e_{h}=c_2 {\rm e}^{-\lambda t}$,where $c_1$,$c_2$ are undetermined constants,$e$ is the natural exponent. Therefore, $e_{v}$ and $e_{h}$ can asymptotically converge to zero,$v$ and $h$ can track reference signals $v_r$ and $h_r$,respectively.
Remark 3. The figure of the function $|s_{r_i}|^{o_i}\textrm{sgn}(s_{r_i})$ is presented in Fig. 2. It is obvious that the function is continuous. Therefore,the control law in (27) is also continuous. For the continuous controller,the chattering is eliminated. Note that system states arrive at a small neighborhood of $s_{r_i}$,$i=1,2$ before observation errors $e_{d_i}(t)$ reach zero,which is considered to be the cost of eliminating the chattering. The boundary layer method keeps the width of convergence region no matter what $e_{d_i}(t)$ is,and the convergence is asymptotical to the small region. The proposed method enables the asymptotical convergence to zero when $e_{d_i}(t)$ reaches zero and avoids chattering.
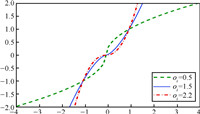
|
Download:
|
| Fig. 2. The continuous function $ |{s_{{r_i}}}{|^{{o_i}}}$ sgn $ {s_{{r_i}}}$ different oi values. | |
Remark 4. The terms $-\ell_1 \textrm{sig}^{o_1}(s_{r_i})-\ell_2\textrm{sig}^{o_2}(s_{r_i})$ in the control law (27) can increase the convergence rate. When system states are far away from $s_{r_i}=0$,the term $- \ell_2 \textrm{sig}^{o_2} (s_{r_i})$ would accelerate the convergence. When system states are very close to $s_{r_i}=0$,the term $- \ell_1 \textrm{sig}^{o_1} (s_{r_i})$ help the convergence. Refer to Fig. 2,$|s_{r_i}|^{o_i}\textrm{sgn}(s_{r_i})$ with $o_i=0.5$, $o_i=1.5$ and $o_i=2.2$.
Ⅳ. SIMULATIONIn this section,simulation is executed to demonstrate the effectiveness of the proposed method.
As a representative case study,the hypersonic vehicle is assumed to trim at $v=15\,060\,\mathrm{ft/s}$ and $h=110\,000\,\mathrm{ft}$,and the aerodynamic coefficients and model parameters are given in Table Ⅰ
|
|
Table Ⅰ AERODYNAMIC AND INERTIAL COEFFICIENTS |
Parameters of the sliding mode controller are $\lambda_v=\lambda_h=1$,$\ell_{1}=\ell_{2}=10$,$o_{1}=0.6$ and $o_{2}=1.5$. Parameters of disturbance observer are designed as $\lambda_0=3$,$\lambda_1=1.5$,$\lambda_2=1.1$,$L_1=15$, $L_2=50$.
A. Tracking ControlThe reference velocity is $14\,960\,\mathrm{ft/s}$ and the reference altitude is $110\,200\,\mathrm{ft}$. During the tracking process, the vehicle is perturbed by
| $ \begin{align} \bar{d}(t)=\begin{cases}0,\quad \text{if} \quad 0\leq t < 1,\\ \begin{bmatrix} 0.1+0.05 \sin(0.4t) \\ -0.02-0.05\sin(0.4t) \end{bmatrix},\quad \text{if} \quad t \geq 1 \end{cases} \end{align} $ | (29) |
The continuous sliding mode controller is adopted,where the finite time disturbance observer is used as the compensator to reject disturbance. Figs. 3 (a) and 3 (b) show that the designed observer can work effectively to exactly estimate disturbances in finite time,where dotted lines represent actual disturbances and solid lines depict observed values. The observed values $z^1_1$ and $z^2_1$ have well approximation to disturbances $\bar{d}_1$ and $\bar{d}_2$ after a finite time.
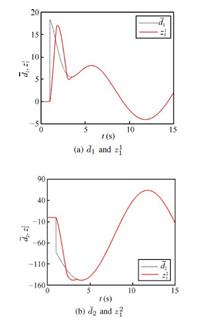
|
Download:
|
| Fig. 3. Real disturbance values and estimated values. | |
As stated in Theorem 1,before estimated errors become zero,the velocity switching mode and the altitude switching mode arrive at small regions with respect to estimated errors. In other words,if the track error of velocity $e_{d_1}(t) \neq 0$,$e_v$ reaches the $\psi_v$ region of $s_v=0$,where $\psi_v= \min \{|\frac{e_{d_1}(t)}{\ell_1}|^{\frac{1}{o_1}}, |\frac{e_{d_1}(t)}{\ell_2}|^{\frac{1}{o_2}} \}$. For the same reason,if the tracking error $e_{d_2}(t) \neq 0$ of altitude, $e_h$ also runs into the $\psi_h$ region of $s_h=0$,where $\psi_h= \min \{|\frac{e_{d_2}(t)}{\ell_1}|^{\frac{1}{o_1}}, |\frac{e_{d_2}(t)}{\ell_2}|^{\frac{1}{o_2}} \}$. Once tracking errors $e_{d_i}(t)$ stabilizes to zero after a finite time,system states also reach $s_v=0$ and $s_h=0$ in finite time. Fig.4 presents the boundaries of the two small regions,where $\psi^v$ and $\psi^h$ with solid lines describe positive boundaries for velocity and altitude switching modes,and $\psi^v_1$,$\psi^v_2$, $\psi^h_1$ and $\psi^h_2$ express $|\frac{e_{d_1}(t)}{\ell_1}|^{\frac{1}{o_1}}$, $|\frac{e_{d_1}(t)}{\ell_2}|^{\frac{1}{o_2}}$, $|\frac{e_{d_2}(t)}{\ell_1}|^{\frac{1}{o_1}}$ and $|\frac{e_{d_2}(t)}{\ell_2}|^{\frac{1}{o_2}}$,respectively.
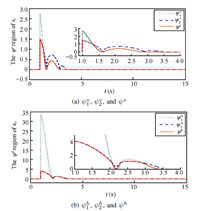
|
Download:
|
| Fig. 4. The positive boundaries of velocity and altitude switching modes. | |
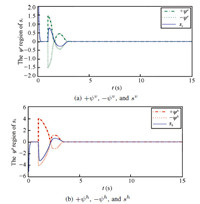
Fig. 5 further describes curves of $s_v$ and $s_h$,which locate in small regions before tracking errors reach zero,restrained by $|s_v| \leq \psi^v$ and $|s_h| \leq \psi^h$.
|
Download:
|
| Fig. 5. Switching mode variables located in their regions. | |
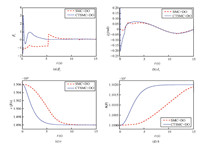
Fig. 6 provides the continuous control laws $\beta_c$ and $\delta_e$ to avoid the chattering. Simultaneously,tracking results of velocity and altitude are also displayed in Fig. 6, where velocity and altitude are both asymptotically stabilize at their reference commands. It exhibits good robustness against disturbances with the composite controller. The boundary layer method is executed to compare with the proposed method. The sign function is replaced by the saturation function and the finite time disturbance observer is still used as the compensator. The width of the saturation function is $\tau= 0.5$,the gain $l_1 = 20$. The simulation results are illustrated in Fig. 6 with dashed lines. The chattering has been eliminated,but the system responses are still slower than that with the proposed method.
|
Download:
|
| Fig. 6. Control laws and output responses, continuous TSMC with DO, saturation SMC with DO. | |
It can be observed that the composite control has finished the tracking of velocity and altitude within ten seconds in the previous simulation. The hypersonic aircraft is expected to track step commands,where $v_r=14\,960\,\mathrm{ft/s}$ and $h_r=110\,200\,\mathrm{ft}$ change to $v_r=14\,870\,\mathrm{ft/s}$ and $h_r=110\,360\,\mathrm{ft}$ at $t=20$ s. The disturbances also change at $t=35$ s,which are designed as follows:
| $ \begin{align} &\bar{d}_1(t)=\begin{cases}0,0\leq t < 1,\\ 0.1+0.05\sin(0.4 t),1 \leq t < 35 ,\\ 0.1+0.05\sin(0.4 t)-0.1\cos(0.2t),\ t \geq 35. \end{cases} \end{align} $ | (30) |
| $ \begin{align} &\bar{d}_2(t)=\begin{cases}0,0\leq t < 1,\\ -0.02-0.05\sin(0.4t), 1 \leq t < 35 ,\\ -0.02-0.05\sin(0.4t)+0.02\cos(0.2t),t \geq 35. \end{cases} \end{align} $ | (31) |
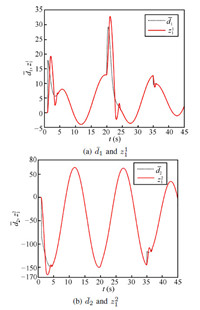
The robustness of controller is checked here. All parameters are set the same as the previous simulation. The varying disturbances are effectively estimated by the finite time observer,shown in Fig. 7,where dotted lines represent disturbances,solid lines are provided by estimated values.
|
Download:
|
| Fig. 7. Estimated values for ${{\bar d}_1}$ and ${{\bar d}_2}$. | |
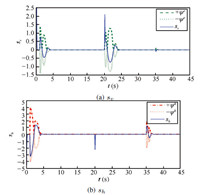
Fig. 8 presents new boundaries of $s_v$ and $s_h$ considering new varying disturbances. Switching mode variables $s_v$ and $s_h$ are firstly restrained to small regions,and then the two switching mode variables arrive at zero when estimated errors converge to zero.
|
Download:
|
| Fig. 8. Switching modes and their regions. | |
The continuous control laws illustrated in Fig. 9. $v$ and $h$ keep convergent to reference signals,where the robustness of the continuous controller is illustrated. Velocity and altitude are not perturbed even if new disturbances are added at $t=35$ s, and still keep well tracking to step reference signals.

|
Download:
|
| Fig. 9. Control laws and output responses. | |
In this paper,a composite continuous controller is discussed for the tracking problem of hypersonic vehicles. The system model is linearized to velocity and altitude subsystems. The continuous controller is designed to reduce chattering. The finite time disturbance observer is introduced to reject disturbances. Because the discontinuous term is replaced by continuous terms,switching modes of velocity and altitude arrive at small regions which vary depending on disturbance observation errors. When observation errors disappear,the observer converges to disturbance signals in finite time. It turns out that restrained regions to switching modes become zero and tracking errors of velocity and altitude asymptotically converge to zero. The method has significantly improved boundary layer method. Simulations have proved the effectiveness of the proposed continuous sliding mode control with disturbance observer for the tracking control of AHVs and high convergence rate is also provided.
APPENDIX ANomenclature:
$v-$speed of sound
$\gamma-$flight-path angle
$h-$altitude
$\alpha-$angle of attack
$q-$pitch rate
$T-$thrust
$D-$drag
$L-$lift
$C_{T}(\beta)-$thrust coefficient
$C_{D}(\alpha)-$drag coefficient
$C_{L}(\alpha)-$lift coefficient
$C_{M}(q)-$pitch rate contribution to moment
$C_{M}(\alpha)-$angle of attack contribution to moment
$C_{M}(\delta_{e})-$elevator deflection contribution to moment
$m-$mass
$R_{E}-$radius of the Earth
$R-$radial distance from Earth$'$s center
$\bar{c}-$mean aerodynamic chord
$c_{\beta}-$throttle coefficient in $C_{T}$
$c_e-$elevator coefficient in $C_{M}(\delta_{e})$
$I_{yy}-$moment of inertia
$M_{yy}-$pitching moment
$S-$reference area
$\delta_{E}-$elevator angular deflection
$\beta-$throttle setting
$\beta_c-$control contribution to throttle setting $\beta$
$w_n-$natural frequency for throttle setting $\beta$
$\xi-$damping ratio for throttle setting $\beta$
$\mu-$gravitational constant
$\rho-$density of air
Expression:
| $ \begin{align} &\dot{x}=[\dot{v},\dot{\gamma},\dot{\alpha},\dot{\beta},\dot{h}]^{\mathrm{T}} \\ \quad &\ddot{x}=[\ddot{v},\ddot{\gamma},\ddot{\alpha},\ddot{\beta},\ddot{h}]^{\mathrm{T}} \\ \quad &\ddot{x}_{0}=[\ddot{v},\ddot{\gamma},\ddot{\alpha}_{0},\ddot{\beta}_{0},\ddot{h}]^{\mathrm{T}} \\ \quad &\ddot{\alpha}_{0}=\frac{1}{2I_{yy}}\rho v^{2}S\bar{c}(C_{M}(\alpha)+C_{M}(q)-c_{e}\alpha)-\ddot{\gamma}\\ \quad &\ddot{\beta}_{0}=-2\xi w_{n}\dot{\beta}-w_{n}^{2}\beta \\ &\dot{\gamma}=f_2(x), \ddot{\gamma}=\tilde{\pi}\dot{x}, \gamma^{(3)}=\tilde{\pi}\ddot{x}+\dot{x}^{\mathrm{T}}\Pi\dot{x} \\ &c_{\beta}=\left\{\begin{array}{ll} 0.02576,& \text{if} \quad \beta < 1 \\ 0.003360,& \text{if} \quad \beta>1 \end{array}\right. \\ \end{align} $ |
| $ \begin{align} &D_{\alpha}=\frac{1}{2}\rho v^{2}S(1.290\alpha+0.0043378)\notag\\ &L_{\alpha}=\frac{1}{2}\rho v^{2}S\,\times\,0.6203 \\ \tilde{w}&=\frac{\partial \dot{v}}{\partial x}=\left[\frac{\partial \dot{v}}{\partial v},\frac{\partial \dot{v}}{\partial \gamma},\frac{\partial \dot{v}}{\partial \alpha},\frac{\partial \dot{v}}{\partial \beta},\frac{\partial \dot{v}}{\partial h}\right]= \\ &\begin{bmatrix} \frac{\partial T}{\partial v}\cos \alpha - \frac{\partial D}{\partial v}\\[2mm] -m \mu \frac{\cos \gamma}{R^2} \\[2mm] \frac{\partial T}{\partial \alpha}\cos \alpha-T \sin \alpha - \frac{\partial D}{\partial \alpha}\\[2mm] \frac{\partial T}{\partial \beta}\cos \alpha\\[2mm] \frac{\partial T} {\partial h}\cos \alpha - \frac{\partial D}{\partial h} + \frac{\partial R}{\partial h}(2m \mu \frac{\sin \gamma }{R^3}) \end{bmatrix}^{\mathrm{T}} \\ \tilde{\pi}&=\frac{\partial \dot{\gamma}}{\partial x}=\left[\frac{\partial \dot{\gamma}}{\partial v},\frac{\partial \dot{\gamma}}{\partial \gamma},\frac{\partial \dot{\gamma}}{\partial \alpha},\frac{\partial \dot{\gamma}}{\partial \beta},\frac{\partial \dot{\gamma}}{\partial h}\right]= \\ &\begin{bmatrix} \frac{\frac{\partial L}{\partial v }+ \frac{\partial T}{\partial v } \sin \alpha} {m v} -\frac{L+T\sin \alpha}{m v^2} + \frac{\mu \cos \gamma}{v^2 R^2}+ \frac{\cos \gamma}{R}\\[2mm] \frac{\mu \sin \gamma}{vR^2}-\frac{v \sin \gamma}{R}\\[2mm] \frac{\frac{\partial L}{\partial \alpha}+ \frac{\partial T}{\partial \alpha } \sin \alpha + T\cos \alpha}{m v} \\[2mm] \frac{\frac{\partial T} {\partial \beta}\sin \alpha }{mv}\\[2mm] \frac{\frac{\partial L}{\partial h}+ \frac{\partial T}{\partial h } \sin \alpha }{mv}+ \frac{ 2 \mu \cos \gamma \frac{\partial R}{\partial h}}{vR^{3}}-\frac{v\cos \gamma \frac{\partial R} {\partial h} }{R^2} \end{bmatrix}^{\mathrm{T}} \\ &\Omega=\frac{\partial \tilde{w}}{\partial x}=\left[\frac{\partial \tilde{w}_1}{\partial x}, \frac{\partial \tilde{w}_2}{\partial x},\frac{\partial \tilde{w}_3}{\partial x}, \frac{\partial \tilde{w}_4}{\partial x},\frac{\partial \tilde{w}_5}{\partial x}\right] \\ &\frac{\partial \tilde{w}_1}{\partial x}=\begin{bmatrix} \frac{\partial^{2} T} {\partial v^{2}}\cos \alpha -\frac{\partial^{2} D}{\partial v^{2}} \\ 0\\ \frac{\partial^{2} T}{\partial v \partial \alpha}\cos \alpha - \frac{\partial T} {\partial v}\sin \alpha -\frac{\partial^{2} D}{\partial v \partial \alpha} \\ \frac{\partial^{2} T}{\partial v \partial \beta} \cos \alpha \\ \frac{\partial^{2} T} {\partial v \partial h} \cos \alpha - \frac{\partial^{2} D}{\partial v\partial h} \end{bmatrix} \\ &\frac{\partial \tilde{w}_2}{\partial x}=\begin{bmatrix} 0 \\ m \mu \frac{\sin \gamma}{R^2} \\ 0 \\ 0 \\\frac{\partial R}{\partial h}(2m \mu \frac{\cos \gamma }{R^3}) \end{bmatrix} \\ & \frac{\partial \tilde{w}_3}{\partial x}=\begin{bmatrix} \frac{\partial^{2} T} {\partial v \partial \alpha}\cos \alpha -\frac{\partial T}{\partial v}\sin \alpha - \frac{\partial^{2} D}{\partial v \partial \alpha} \\[1mm] 0\\[1mm] \frac{\partial^{2} T}{\partial \alpha^{2}}\cos \alpha - 2\frac{\partial T}{\partial \alpha}\sin \alpha -T\cos \alpha - \frac{\partial^{2} D}{\partial \alpha^{2}} \\[1mm] \frac{\partial^{2} T}{\partial \alpha \partial \beta} \cos \alpha - \frac{\partial T}{\partial \beta}\sin \alpha \\[1mm] \frac{\partial^{2} T}{\partial \alpha \partial h} \cos \alpha - \frac{\partial T} {\partial h} - \frac{\partial^{2} D}{\partial \alpha \partial h} \end{bmatrix} \\ & \frac{\partial \tilde{w}_4}{\partial x}=\begin{bmatrix} \frac{\partial^{2} T}{\partial v \partial \beta}\cos \alpha \\0\\ \frac{\partial^{2} T}{\partial \alpha \partial \beta}\cos \alpha - \frac{\partial T}{\partial \beta}\sin \alpha \\ \frac{\partial^{2} T}{\partial \beta^{2}} \cos \alpha \\ \frac{\partial^{2} T}{\partial \beta \partial h} \cos \alpha \end{bmatrix} \\ & \frac{\partial \tilde{w}_5}{\partial x}=\begin{bmatrix} \frac{\partial^{2} T}{\partial v \partial h}\cos \alpha -\frac{\partial^{2} D}{\partial v \partial h} \\[1mm] \frac{\partial R} {\partial h} (2 m \mu \frac{\cos \gamma }{R^3})\\[1mm] \frac{\partial^{2} T}{\partial \alpha \partial h} \cos \alpha - \frac{\partial T}{\partial h}\sin \alpha -\frac{\partial^{2} D}{\partial \alpha \partial h} \\[1mm] \frac{\partial^{2} T}{\partial \beta \partial h} \cos \alpha \\[1mm] \frac{\partial^{2} T} {\partial h^{2}} \cos \alpha - \frac{\partial^{2} D}{\partial h^{2}}-(\frac{\partial R} {\partial h})^{2}(6 m \mu \frac{\sin \gamma}{R^{4}}) \end{bmatrix}\\ &\Pi=\frac{\partial \tilde{\pi}}{\partial x}=\left[\frac{\partial \tilde{\pi}_1}{\partial x}, \frac{\partial \tilde{\pi}_2}{\partial x},\frac{\partial \tilde{\pi}_3}{\partial x}, \frac{\partial \tilde{\pi}_4}{\partial x},\frac{\partial \tilde{\pi}_5}{\partial x}\right] \end{align} $ |
| $ \begin{align} & \scriptstyle \dfrac{\partial \tilde{\pi}_1}{\partial x}=\begin{bmatrix} \scriptstyle \frac{ \frac{\partial^{2} L}{\partial v^{2} }+ \frac{\partial^{2} T}{\partial v^{2} } \sin \alpha}{m v} -\frac{2(\frac{\partial L}{\partial v}+ \frac{\partial T}{\partial v} \sin \alpha)}{m v^2} +\frac{2( L+ T \sin \alpha)}{m v^3} - \frac{2 \mu \cos \gamma}{v^3 R^2}\\[1mm] \scriptstyle - \frac{ \mu \sin \gamma}{v^2 R^2} - \frac{ \sin \gamma}{R} \\[1mm] \scriptstyle \frac{ \frac{\partial^{2} L}{\partial v \partial \alpha }+ \frac{\partial^{2} T} {\partial v \partial \alpha} \sin \alpha+ \frac{\partial T}{\partial v }\cos \alpha }{m v} -\frac{ \frac{\partial L}{\partial \alpha}+ \frac{\partial T}{\partial \alpha} \sin \alpha +T \cos \alpha }{m v^2} \\[1mm] \scriptstyle \frac{\frac{\partial^{2} T}{\partial v \partial \beta }\sin \alpha }{m v}- \frac{\frac{\partial T}{\partial \beta} \sin \alpha}{m v^2} \\[1mm] \scriptstyle \frac{ \frac{\partial^{2} L}{\partial v \partial h }+ \frac{\partial^{2} T} {\partial v \partial h } \sin \alpha}{m v} -\frac{\frac{\partial L}{\partial h}+ \frac{\partial T}{\partial h} \sin \alpha }{m v^2}- \frac{2 \mu \cos \gamma \frac{\partial R} {\partial h} }{v^2 R^3} - \frac{ \cos \gamma \frac{\partial R}{\partial h} }{R^2} \end{bmatrix} \\ & \frac{\partial \tilde{\pi}_2}{\partial x}= \begin{bmatrix} - \frac{\mu \sin \gamma} {v^2 R^2} -\frac{\sin \gamma}{R} \\[1mm] \frac{ \mu \cos \gamma}{v R^2}-\frac{v \cos \gamma }{R} \\0\\0\\ - \frac{ 2 \mu \sin \gamma \frac{\partial R }{\partial h}}{vR^3}+ \frac{v \sin \gamma \frac{\partial R } {\partial h} }{ R^2}\end{bmatrix} \\ & \frac{\partial \tilde{\pi}_3}{\partial x}=\begin{bmatrix} \frac{ \frac{\partial^{2} L} {\partial v \partial \alpha}+ \frac{\partial^{2} T}{\partial v \partial \alpha } \sin \alpha + \frac{\partial T}{\partial v } \cos \alpha }{m v} -\frac{ \frac{\partial L}{\partial \alpha}+ \frac{\partial T}{\partial \alpha} \sin \alpha +T\cos \alpha}{m v^2} \\0\\ \frac{ \frac{\partial^{2} L}{\partial \alpha^{2} }+ \frac{\partial^{2} T}{\partial \alpha^{2}} \sin \alpha+ 2\frac{\partial T}{\partial \alpha }\cos \alpha - T \sin \alpha }{m v} \\ \frac{ \frac{ \partial^{2} T}{\partial \alpha \partial \beta} \sin \alpha +\frac{\partial T}{\partial \beta} \cos \alpha }{m v} \\ \frac{\frac{\partial^{2} L}{\partial \alpha \partial h} + \frac{\partial^{2} T} {\partial \alpha \partial h }\sin \alpha+ \frac{\partial T}{\partial h} \cos \alpha} {m v}\end{bmatrix} \end{align} $ |
| $ \begin{align} & \frac{\partial \tilde{\pi}_4}{\partial x}=\begin{bmatrix} \frac{ \frac{ \partial^{2} T} {\partial v \partial \beta} \sin \alpha}{mv}-\frac{ \frac{ \partial T}{\partial \beta} \sin \alpha}{mv^2}\\0\\ \frac{ \frac{ \partial^{2} T}{\partial \alpha \partial \beta} \sin \alpha + \frac{ \partial T}{\partial \beta} \cos \alpha }{mv}\\[1mm] \frac{ \frac{ \partial^{2} T}{\partial \beta^{2}} \sin \alpha}{mv} \\[1mm] \frac{ \frac{ \partial^{2} T}{\partial \beta \partial h } \sin \alpha}{mv}\end{bmatrix} \\ \\ &\scriptstyle \dfrac{\partial \tilde{\pi}_5}{\partial x}=\begin{bmatrix}\scriptstyle \frac{ \frac{\partial^{2} L}{\partial v \partial h}+ \frac{\partial^{2} T}{\partial v \partial h } \sin \alpha}{m v} -\frac{ \frac{\partial L}{\partial h}+ \frac{\partial T}{\partial h} \sin \alpha} {m v^2} - \frac{2\mu \cos \gamma\frac{\partial R}{\partial h}}{ v^2 R^3} - \frac{ \cos \gamma \frac{\partial R}{\partial h} }{ R^2}\\[1mm] \scriptstyle - \frac{2 \mu \sin \gamma \frac{\partial R}{\partial h}}{v R^3}+ \frac{v \sin \gamma \frac{\partial R}{\partial h}}{R^{2}} \\[1mm] \scriptstyle \frac{ \frac{\partial^{2} L}{\partial \alpha \partial h}+ \frac{\partial^{2} T}{\partial \alpha \partial h} \sin \alpha + \frac{\partial T}{\partial h}\cos \alpha }{m v} \\[1mm] \scriptstyle \frac{\frac{\partial^{2} T}{\partial \beta \partial h }\sin \alpha }{m v} \\[1mm] \scriptstyle \frac{ \frac{\partial^{2} L}{\partial h^{2} }\scriptstyle+ \frac{\partial^{2} T} {\partial h^{2} } \sin \alpha}{m v} \scriptstyle - \frac{6 \mu \cos \gamma (\frac{\partial R} {\partial h} )^{2}}{vR^4}\scriptstyle + \frac{2v \cos \gamma ( \frac{\partial R}{\partial h})^{2} } {R^3} \end{bmatrix} \end{align} $ |
Considering the system $\dot{x}(t)=y(t)+g(t)$,all derivatives $\dot{g}(t)$,$\ddot{g}(t)$,$\cdots$,$g^{(p-1)}(t)$ of the disturbance term $g(t)$ are assumed to be bounded,such that there is a known Lipshitz constant $L>0$ for $g^{(p-1)}(t)$.
For a continuous function $x(t)$ defined $t \geq 0$,if $y(t)$ is Lebesgue-measurable,when input noises of $x(t)$ and $y(t)$ are zero,the exact finite time observer for $g(t)$ can be established as follows:
| $ \begin{align*} \begin{cases} \dot{z}_0=\nu_0+ y,\\ \nu_0=- \lambda_0 L ^{ \frac{1}{p+1} } |z_0 - x |^{ \frac{p}{p+1} } \textrm{sgn} (z_0 - x) + z_1 ,\\ \dot{z}_1=\nu_1,\\ \nu_1=- \lambda_1 L ^{ \frac{1}{p} } | z_1 - \nu_0 |^{ \frac{p-1}{p} } \textrm{sgn} ( z_1 - \nu_0 ) + z_2,\\ \qquad \vdots \\ \dot{z}_{p-1}=\nu_{p-1},\\ \nu_{p-1}= - \lambda_{p-1} L ^{ \frac{1}{2} } | z_{p-1} - \nu_{p-2} |^{ \frac{1}{2} } \textrm{sgn} ( z_{p-1} - \nu_{p-2} ) + z_m,\\ \dot{z}_{p}= - \lambda_{p} L \textrm{sgn} ( z_{p} - \nu_{p-1} ), \end{cases} \end{align*} $ |
with enough large parameters $\lambda_i$,$i=0,\cdots,p$,$z_0$,$z_1$, $\cdots$,$z_p$ can converge to $x$,$g(t)$,$\cdots$,$g^{(p-1)}(t)$ in finite time.
| [1] | Fidan B, Mirmirani M, Ioannou P A. Flight dynamics and control of air-breathing hypersonic vehicles:review and new directions. In:Proceedings of the 2003 AIAA International Space Planes and Hypersonic Systems and Technologies. Norfolk, USA:AIAA, 2003. |
| [2] | Fiorentini L, Serrani A, Bolender M A, Doman D B. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles. Journal of Guidance, Control, and Dynamics, 2009, 32(2):401-416 |
| [3] | Sigthorsson D O, Jankovsky P, Serrani A, Yurkovich S, Bolender M, Doman D B. Robust linear output feedback control of an air-breathing hypersonic vehicle. Journal of Guidance, Control, and Dynamics, 2008, 31(4):1052-1065 |
| [4] | Zhu Y J, Shi Z K. Several problems of flight characteristics and flight control for hypersonic vehicles. Flight Dynamics, 2005, 23(3):5-8 |
| [5] | Gregory I M, McMinn J D, Chowdhry R S, Shaughnessy J D. Hypersonic Vehicle Model and Control Law Development Using H∞ and μ Synthesis, NASA Technical Memorandum, USA, NASA TM-4562, 1994. |
| [6] | Lind R. Linear parameter-varying modeling and control of structural dynamics with aero-thermodynamic effects. Journal of Guidance, Control, and Dynamics, 2002, 25(4):733-739 |
| [7] | Oppenheimer M W, Doman D B. Control of an unstable, nonminimum phase hypersonic vehicle model. In:Proceedings of the 2006 Aerospace Conference. Big Sky, MT:IEEE, 2006. 1-22 |
| [8] | Gibson T E, Annaswamy A M. Adaptive control of hypersonic vehicles in the presence of thrust and actuator uncertainties. In:Proceedings of the 2008 AIAA Guidance, Navigation and Control Conference and Exhibit. Hawali, USA:AIAA, 2008. |
| [9] | Serrani A, Zinnecker A M, Fiorentini L, Bolender M A, Doman D B. Integrated adaptive guidance and control of constrained nonlinear air-breathing hypersonic vehicle models. In:Proceedings of the 2009 American Control Conference. St. Louis, USA:IEEE, 2009. 3172-3177 |
| [10] | Wang Q, Stengel R F. Robust nonlinear control of a hypersonic aircraft. Journal of Guidance, Control, and Dynamics, 2000, 23(4):577-585 |
| [11] | Xu J H, Mirmirani M, loannou P A. Adaptive sliding mode control design for a hypersonic flight vehicle. Journal of Guidance, Control, and Dynamics, 2004, 27(5):829-838 |
| [12] | Bowcutt K G. Multidisciplinary optimization of airbreathing hypersonic vehicles. Journal of Propulsion and Power, 2001, 17(6):1184-1190 |
| [13] | Jiang C H, Zhang C Y, Zhu L. Research of robust adaptive trajectory linearization control based on T-S fuzzy system. Journal of Systems Engineering and Electronics, 2008, 19(3):537-545 |
| [14] | Zhu L, Jiang C S, Zhang C Y. Adaptive trajectory linearization control for aerospace vehicle based on RBFNN disturbance observer. Acta Aeronautica et Astronautica Sinica, 2007, 28(3):673-677 |
| [15] | Hu X X, Wu L G, Hu C H, Gao H J. Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle. Journal of the Franklin Institute, 2012, 349(2):559-577 |
| [16] | Yu S H, Yu X H, Shirinzadeh B, Man Z H. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica, 2005, 41(11):1957-1964 |
| [17] | Slotine J J, Sastry S S. Tracking control of non-linear systems using sliding surfaces with application to robot manipulators. International Journal of Control, 1983, 38(2):465-492 |
| [18] | Slotine J J, Li W P. Applied Nonlinear Control. New Jersey:Prentice Hall, 1991. |
| [19] | Li S H, Sun H B, Sun C Y. Composite control design for an air-breathing hypersonic vehicle. Proceedings of the Institution of Mechanical Engineers, Part I:Journal of Systems and Control Engineering, 2012, 226(5):651-664 |
| [20] | Sun H B, Li S H, Sun C Y. Finite time integral sliding mode control of hypersonic vehicles. Nonlinear Dynamics, 2013, 73(1-2):229-244 |
| [21] | Zong Q, Ji Y H, Zeng F L, Liu H L. Output feedback back-stepping control for a generic hypersonic vehicle via small-gain theorem. Aerospace Science and Technology, 2012, 23(1):409-417 |
| [22] | Zong, Q, Wang J, Tao Y. Adaptive high-order dynamic sliding mode control for a flexible air-breathing hypersonic vehicle. International Journal of Robust Nonlinear Control, 2013, 23(15):1718-1736 |
| [23] | Sigthorsson D O, Jankovsky P, Serrani A, Yurkovich S, Bolender M, Doman D B. Robust linear output feedback control of an air-breathing hypersonic vehicle. Journal of Guidance, Control and Dynamics, 2008, 31(4):1052-1066 |
| [24] | Bolender M A, Doman D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle. Journal of Spacecraft and Rockets, 2007, 44(2):374-387 |
| [25] | Shaughnessy J D, Pinckney S Z. Hypersonic Vehicle Simulation Model:Winged-Cone Configuration, NASA Technical Memorandum, USA, NASA TM-102610, 1991. |
| [26] | Li F H. Guidance and Control Technology of Hypersonic Aircrafts. Beijing:China Astronautic Publishing House, 2012. |
| [27] | Levant A. High-order sliding modes, differentiation and output feedback control. International Journal of Control, 2002, 76(9-10):924-9412 |
| [28] | Shtessel Y B, Shkolnikov A, Levant A. Smooth second-order sliding modes:missile guidance application. Automatica, 2007, 43(8):1470-1476 |
| [29] | Levant A. Robust exact differentiation via sliding mode technique. Automatica, 1998, 34(3):379-384 |
 2015, Vol.2
2015, Vol.2 


