Nowadays,unmanned aerial vehicles (UAVs) have been widely used in both military and civilian areas due to their low cost,high maneuverability,no casualty,etc[1, 2, 3, 4]. In a sense, UAVs show a valuable prospect for some applications where human interventions are restricted. To achieve a successful mission,the robust adaptive tracking control design for UAVs needs to be excellent because of the absence of a human pilot. Thus,it has attracted an increasing interest around the world in recent years. In [5],a high-level controller for a fixed-wing UAV was developed based on the nonlinear model predictive control method through an error dynamics. In [6],the output-feedback control scheme was proposed for an underactuated quadrotor UAV using neural networks. In [7],an optimal controller was designed for helicopter UAVs,and the optimal trajectory tracking was accomplished by a single neural network. To increase the robustness,a sliding mode controller and an adaptive controller were presented in [8] and [9],respectively. However,as a kind of multi-input and multi-output (MIMO) nonlinear systems,the design of robust flight control is complex for UAVs with parameter uncertainty,strong nonlinearity,high coupling and unknown external disturbance. Fortunately,the nonlinear disturbance observer (NDO) is proven to be an effective method to handle system uncertainty and unknown external disturbance[10, 11, 12, 13, 14]. The robust control design based on the NDO has been successfully applied to air vehicles. In [10, 11, 12, 13],under the condition that the derivative of the compounded disturbance was closely equal to zero,a disturbance observer technique was proposed. Actually,the compounded disturbance is changeable with time for UAVs. To relax this assumption of the above mentioned NDO,we need to further develop and apply it to the robust control design of UAVs.
For some special classes of nonlinear systems,backstepping is an important control approach[15, 16, 17, 18, 19],which is a Lyapunov-based recursive design procedure. In [16, 17, 18],an adaptive tracking control framework for a class of uncertain nonlinear systems was studied based on radial basis function neural networks. The adaptive control scheme was developed for MIMO nonlinear systems considering time-varying delays and unknown backlash-like hysteresis in [19]. However,there exists the problem of calculation explosion in the conventional backstepping technique. The dynamic surface control (DSC)[20, 21, 22, 23, 24] was proposed to solve this problem by introducing a first-order filter at each step. As a result,the derivative of the virtual control law was avoided to be calculated,which simplified the design process. In [20],the dynamic surface technique was described in detail by Swaroop et al.,and further developed in [21, 22, 23, 24]. In this paper, the robust adaptive tracking control for UAVs is designed based on the DSC.
On the other hand,the rudder deflections of UAVs are limited. If we ignore input saturation in the control design,the system control performance can be degraded and the system instability can be caused,even a serious accident will happen. During the past decades,various schemes for the control design of nonlinear systems with input saturation have been studied extensively. In [25, 26, 27],a robust adaptive control was proposed based on the backstepping technique,using the special property of a hyperbolic tangent function and a Nussbaum function to handle the input saturation. In [28, 29, 30],an auxiliary system was constructed as a compensator to eliminate the effect of the input saturation,which was successfully applied to the control design of ocean surface vessels. By regarding the input saturation as a kind of constraints for the optimization function,the predictive control was studied[31, 32]. In [33, 34],an adaptive dynamic programming approach was proposed by employing a generalized non-quadratic function to deal with control constraints. However, there are few existing works about tracking control for UAVs with input saturation and unknown external disturbance.
Motivated by the above discussion and analysis,a robust adaptive tracking control scheme is proposed for a class of uncertain MIMO nonlinear systems in the presence of system uncertainty,unknown external disturbance,and input saturation. To efficiently handle the compounded disturbance,the NDO is employed. The auxiliary system is designed to eliminate the effect of input saturation. The advantage of the dynamic surface technique is taken to deal with the explosion of complexity in backstepping control. The stability of the closed-loop system based on the developed robust adaptive tracking control scheme is rigorously analyzed through Lyapunov method. Finally,the developed robust adaptive tracking control scheme is used for the flight control design of UAVs. The organization of the paper is as follows. In Section Ⅱ,the problem is described. Section Ⅲ presents the design of the NDO. The robust adaptive tracking control is investigated for uncertain MIMO nonlinear systems by considering system uncertainty,unknown external disturbance,and input saturation in Section Ⅳ. In Section Ⅴ,simulation results of a UAV are given to illustrate its effectiveness,followed by concluding remarks in Section Ⅵ.
Ⅱ. PROBLEM STATEMENTConsider a class of uncertain MIMO nonlinear systems in the presence of input saturation,given as follows:
| $\begin{array}{l} {{\dot x}_i} = {F_i}({{\bar x}_i}) + {G_i}({{\bar x}_i}){x_{i + 1}} + {D_i}({{\bar x}_i},t),i = 1,2,\cdots ,k - 1,\\ {{\dot x}_k} = {F_k}({{\bar x}_k}) + {G_k}({{\bar x}_k})u(v) + {D_k}({{\bar x}_k},t),\\ y = {x_1}, \end{array}$ | (1) |
where $ x_i=[x_{i,1},x_{i,2},\cdots,x_{i,n}]\in {\bf R}^{n}$ is the state vector,$ y\in {\bf R}^{n}$ is the output vector, $\bar{ x}_i={[x^{\rm T}_{1},x^{\rm T}_{2},\cdots,x^{\rm T}_{i}]}^{\rm T}\in {\bf R}^{in}$,$ F_i({\bar{ x}_i})\in {\bf R}^{n}$,$ G_j({\bar{ x}_j})\in {\bf R}^{n\times n}$ and $ G_k({\bar{ x}_k})\in {\bf R}^{n\times m}$ are known smooth nonlinear functions of the state vector,${ D}_i(\bar{ x}_i,t)=\Delta{ F_i}(\bar{ x}_i)+{ d}_{ei}(t)$ is the unknown compounded disturbance, $\Delta{ F_i}(\bar{ x}_i)$ stands for the system uncertainty,${ d}_{ei}(t)$ represents the external disturbance,$i=1,2,\cdots,k$,$j=1,2,\cdots,k-1$,$ v\in {\bf R}^{m}$ is the control input vector,$ u( v)\in {\bf R}^{m}$ denotes the plant input vector subject to saturation nonlinearity which is described by
| $ \label{eq.problem-02} u_{i} (v_i)={\rm sat}(v_i)=\left\{\begin{array}{ll} {{\rm sgn}(v_i)u_{iM},\,\,\,\,\,|v_{i}|\geq u_{iM}},\\ {v_i,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,|v_{i}|< u_{iM}}, \end{array}\right. $ | (2) |
where $u_{iM}$ is the bound of $u_i(v_i)$,$i=1,2,\cdots,m$,${\rm sgn}(\cdot)$ stands for the sign function.
In this paper,the control objective is designing the adaptive control law $ v$ to make the closed-loop system stable and to rend $ y$ following the given desired trajectory $ y_r$ in the presence of system uncertainty,unknown external disturbance and input saturation,for all initial conditions satisfying $\Pi_i: =\{\sum^{i}_{j=1}( z^{\rm T}_{j} z_{j}+\tilde{\varsigma}^{2}_{j}/{\gamma_j}) +\sum^{i+1}_{j=2} \varepsilon^{\rm T}_{j-1} \varepsilon_{j-1} < 2p_i\}$,where $ z_1= x_1- y_r$,$ z_j= x_j-\alpha_{j-1}$, $\alpha_{j-1}=\varepsilon_{j-1}+\bar{\alpha}_{j-1}$, $\bar{\alpha}_{j-1}$ is the designed virtual control law, $\varepsilon_{j-1}$ is the first-order filter error, $\tilde{\varsigma}_{j}=\bar{\varsigma}_{j}-\hat{\varsigma}_{j}$, $\Vert \tilde{ D}_{j} \Vert \leq \bar{\varsigma}_{j}$, $\tilde{ D}_{j}$ is the approximation error of the disturbance observer,$\hat{\varsigma}_{j}$ is the estimated value of $\bar{\varsigma}_{j}$,$\gamma_j>0$ and $p_i>0$ are designed parameters,$i=1,2,\cdots,k$. To develop the robust adaptive tracking control scheme for the uncertain MIMO nonlinear system (1),the following assumptions and lemmas are required.
Assumption 1. For the uncertain MIMO nonlinear system (1),all states of the system are measurable.
Assumption 2[23]. For the uncertain MIMO nonlinear system (1),the desired trajectory $ y_{r}$ and $\dot{ y}_{r}(t)$,$\ddot{ y}_{r}(t)$ are bounded,that is,there exists a constant $B_0>0$,such that $\Pi_{0}:=\{( y_r,\dot{ y}_{r},\ddot{ y}_{r}):|| y_{r}||^{2}+||\dot{ y}_{r}||^{2}+||\ddot{ y}_{r}||^{2}\leq B_0$},$\Vert \cdot \Vert$ represents the Frobenius norm for a matrix or the Euclidean norm for a vector.
Assumption 3[14]. For the uncertain MIMO nonlinear system (1),the derivative of the compounded disturbance is bounded,that is,$\Vert \dot{ D}_i \Vert \leq \beta_{di}$,where $\beta_{di}>0$ is unknown,$i=1,2,\cdots,k$.
Assumption 4 [35].For the uncertain MIMO nonlinear system (1),the inverse matrix of $ G_i\in {\bf R}^{n\times n}$ exists,$i=1,2,\cdots,k-1$,and the generalized inverse matrix of $ G_k \in {\bf R}^{n\times m}$ exists. On the other hand,there exists positive constant $\bar{\lambda}_i$ making $\lambda_{\max}( G_i G^{\rm T}_{i}) \leq \bar{\lambda}_i$ hold,$i=1,2,\cdots,k$.
Lemma 1[36]. For any ${\rho}>0$ and $\bar{ z}=[\bar{z}_{1},\bar{z}_{2},\cdots,\bar{z}_{n}]^{\rm T}\in {\bf R}^{n}$,the following inequality always holds:
| $ \label{eq.problem-100} 0 < \Vert \bar{ z}\Vert-\bar{ z}^{\rm T}{\rm tanh}(\bar{ z}/{{\rho}})\leq \bar{\kappa}\rho, $ | (3) |
where ${\rm tanh}(\bar{ z}/{\rho})=[{\rm tanh}(\bar{ z}_{1}/{\rho}),{\rm tanh}(\bar{ z}_{2}/{\rho}),\cdots,{\rm tanh}(\bar{ z}_{n}/$ ${\rho})]^{\rm T}$, $\bar{\kappa}=n{\zeta}_{0}$,$n$ is the dimension of vector $\bar{z}$,$\zeta_0$ is a constant satisfying $\zeta_0={\rm e}^{-({\zeta_0}+1)}$,that is,$\zeta_0=0.2785$.
Lemma 2[37]. For bounded initial conditions,if there exists a $C^1$ continuous and positive-definite Lyapunov function $V( x)$ satisfying $\pi_{1}(\Vert x \Vert)\leq V( x)\leq\pi_{2}(\Vert x \Vert)$,such that $\dot{V}( x)\leq-\kappa V( x)+c$,where $\pi_1$,$\pi_2$ : ${\bf R}^{n}\rightarrow {\bf R}$ are class $K$ functions and $\kappa$,$c$ are positive constants,then the solution $ x(t)$ is uniformly bounded.
Remark 1. For a practical system,the derivative of the compounded disturbance should be bounded. Otherwise,the compounded disturbance will be infinite and is quickly changeable with time. This compounded disturbance does not exist in UAV. Thus,Assumption 3 is reasonable.
Ⅲ. DESIGN OF NDOSince the compounded disturbance of the uncertain MIMO nonlinear system (1) is unknown,it cannot be directly used to design the robust adaptive tracking controller. To efficiently deal with this,the NDO is employed. For the convenience of robust adaptive tracking control development,the NDO is described as follows[14].
In a general way,each subsystem of (1) can be written as the following uncertain MIMO nonlinear system given by
| $ \label{eq.problem-03} \dot{ x}= F( x)+ G( x) u+ D( x,t), $ | (4) |
where $ x\in {\bf R}^{n}$ is the state vector,$ u\in {\bf R}^{m}$ is the control input vector,$ F( x)\in {\bf R}^{n}$ and $ G( x)\in {\bf R}^{n\times m}$ are known smooth functions of $ x$,$ D( x,t)=\Delta{ F}( x)+ d_{e}(t)$ is the unknown compounded disturbance, $\Delta{ F}( x)$ stands for the system uncertainty,and $ d_{e}(t)$ represents the external disturbance. $ D( x,t)$ satisfies the assumption of the compounded disturbance,that is,$\Vert \dot{ D} \Vert \leq \beta_{d}$,where $\beta_{d}>0$ is unknown.
To approximate the compounded disturbance of system (4),we design the following NDO:
| $ \label{eq.problem-04} \hat{ D}=\eta+ P( x), $ | (5) |
| $ \label{eq.problem-05} \dot{\eta}=-L\eta-L( P( x)+ F( x)+ G( x) u), $ | (6) |
where $\eta\in {\bf R}^{n}$ is the internal state of the disturbance observer,$ P( x)=[P_{1}( x),P_{2}( x),\cdots,P_{n}( x)]^{\rm T}\in {\bf R}^{n}$ is the designed function vector which should make the constant matrix $L=\frac{\partial P( x)}{\partial x} \in {\bf R}^{n\times n}$ satisfy $2\lambda_{\min}(L)-1>0$.
The error of the disturbance observer is defined as
| $ \label{eq.problem-06} \tilde{ D}= D-\hat{ D}. $ | (7) |
The following lemma about the disturbance observer design is given,which includes the convergence of the disturbance approximation error.
Lemma 3. Consider the uncertain MIMO nonlinear system (4) satisfying the assumption of the compounded disturbance. If the NDO is designed as (5) and (6),then the disturbance approximation error $\tilde{ D}$ is bounded.
Proof. Choose the Lyapunov function as
| $ \label{eq.problem-101} V_0=\frac{1}{2}\tilde{ D}^{\rm T}\tilde{ D}. $ | (8) |
Differentiating (7) and considering (4)~(6),we have
| $\begin{array}{*{35}{l}} \dot{\tilde{D}}=\dot{D}-\dot{\eta }-L\dot{x}= \\ \ \ \ \dot{D}+L\eta +LP-LD= \\ \ \ \ \dot{D}-L\tilde{D}. \\ \end{array}$ | (9) |
Considering (9),the time derivative of $V_0$ is given by
| $\begin{array}{l} {{\dot V}_0} = - {{\tilde D}^{\rm{T}}}L\tilde D + {{\tilde D}^{\rm{T}}}\dot D \le \\ \;\;\;\; - {{\tilde D}^{\rm{T}}}L\tilde D + 0.5{{\tilde D}^{\rm{T}}}\tilde D + 0.5\beta _d^2 \le \\ \;\;\;\; - {\kappa _0}{V_0} + {M_0}, \end{array}$ | (10) |
where $\kappa_0=2\lambda_{\min}(L)-1>0$,and $M_0=0.5\beta^{2}_{d}>0$.
Integration of (10) yields
| $ \label{eq.problem-104} 0\leq V_0\leq\frac{M_0}{\kappa_0}+(V_{0}(0)-\frac{M_0}{\kappa_0}){\rm e}^{-\kappa_0t}. $ | (11) |
According to (11) and Lemma 2,we can obtain that the disturbance approximation error is bounded and satisfies the following inequality:
| $ \label{eq.problem-105} \Vert\tilde{ D}\Vert\leq \sqrt{2V_0}\leq \sqrt{2\left(\frac{M_0}{\kappa_0}+|V_0(0)-\frac{M_0}{\kappa_0}|\right)}. $ | (12) |
This concludes the proof.
Ⅳ. ROBUST ADAPTIVE TRACKING CONTROL DESIGN BASED ON NDOIn this section,the robust adaptive tracking scheme will be proposed for the uncertain MIMO nonlinear system (1) by combining the dynamic surface approach with backstepping technique based on the NDO,and an auxiliary system is constructed to solve the problem of input saturation. The detailed design procedure is described as follows.
Step 1. Employ the NDO to approximate the compounded disturbance $ D_1$ which can be described as
| $ \label{eq.problem-09} \hat{ D}_{1}= \eta_{1}+ P_{1}, $ | (13) |
| $ \label{eq.problem-10} \dot{\eta}_{1}=-L_{1}\eta_{1}-L_{1}( P_{1}+ F_{1}+ G_{1} x_{2}), $ | (14) |
where $\eta_{1}\in {\bf R}^{n}$ is the internal state of the disturbance observer,$ P_{1}\in {\bf R}^{n}$ is the designed function vector,and $L_{1}=\frac{\partial P_{1}}{\partial x_{1}} \in {\bf R}^{n\times n}$. The approximation error of the first disturbance observer is defined as
| $ \label{eq.problem-11} \tilde{ D}_{1}= D_{1}-\hat{ D}_{1}. $ | (15) |
We know that $\tilde{ D}_{1}$ is bounded according to Lemma 3, and assume that $\Vert \tilde{ D}_{1} \Vert \leq\bar\varsigma_{1}$.
Define
| $ \label{eq.problem-12} z_{1}= x_{1}- y_{r}. $ | (16) |
The virtual control law is designed as
| $ {\bar \alpha _1} = G_1^{ - 1}( - {C_1}{z_1} - {F_1} + {\dot y_r} - {\hat D_1} - {\hat \varsigma _1}{\rm{tanh}}({z_1}/{\rho _1})), $ | (17) |
where $C_1=C^{\rm T}_{1}>0$ and $\rho_1>0$ are designed parameters,$\hat{\varsigma}_{1}$ is the estimated value of $\bar\varsigma_{1}$,${\rm tanh}( z_1/{\rho_1})=[{\rm tanh}(z_{1,1}/{\rho_1}),{\rm tanh}(z_{1,2}/{\rho_1}),\cdots,{\rm tanh}(z_{1,n}/{\rho_1})]^{\rm T}$,and $ z_1=[z_{1,1},z_{1,2},\cdots,z_{1,n}]^{\rm T}$.
To solve the explosion of complexity in the traditional backstepping control,the dynamic surface method is employed. Namely,we make the virtual control law $\bar{\alpha}_1$ pass through a first-order filter,i.e.,
| $ \label{eq.problem-14} \Gamma_{1}\dot{\alpha}_1+\alpha_1=\bar{\alpha}_1,~\alpha_1(0)=\bar{\alpha}_1(0), $ | (18) |
where $\Gamma_{1}={\rm diag}\{\tau_{1,1},\tau_{1,2},\cdots,\tau_{1,n}\}$,$\tau_{1,j}>0$ is the time constant of the first-order filter,$j=1,2,\cdots,n$.
Define
| $ \label{eq.problem-15} z_{2}= x_{2}- \alpha_{1}, $ | (19) |
| $ \label{eq.problem-16} \varepsilon_1=\alpha_1 - \bar{\alpha}_1. $ | (20) |
Considering (1) (15) (17) (19) and (20),the time derivative of $ z_1$ can be expressed as
| $ \begin{array}{l} {{\dot z}_1} = {{\dot x}_1} - {{\dot y}_r} = \\ \;\;\;{F_1} + {G_1}{z_2} + {G_1}{\varepsilon _1} + {G_1}{{\bar \alpha }_1} + {D_1} - {{\dot y}_r} = \\ \;\;\; - {C_1}{z_1} + {G_1}{z_2} + {G_1}{\varepsilon _1} + \\ \;\;\;{{\tilde D}_1} - {{\hat \varsigma }_1}{\rm{tanh}}({z_1}/{\rho _1}). \end{array} $ | (21) |
Differentiating (20),we have
| $ \begin{array}{l} {{\dot \varepsilon }_1} = - \Gamma _1^{ - 1}{\varepsilon _1} + ( - \frac{{\partial {{\bar \alpha }_1}}}{{\partial {x_1}}}{{\dot x}_1} - \frac{{\partial {{\bar \alpha }_1}}}{{\partial {z_1}}}{{\dot z}_1} - \frac{{\partial {{\bar \alpha }_1}}}{{\partial {\eta _1}}}{{\dot \eta }_1} + {{\ddot y}_r}) = \\ \;\;\; - \Gamma _1^{ - 1}{\varepsilon _1} + {B_1}({z_1},{z_2},{\varepsilon _1},{\eta _1},{y_r},{{\dot y}_r},{{\ddot y}_r}), \end{array} $ | (22) |
where $ B_{1}(\cdot)$ is a continuous function with respect to variables $( z_1,z_2, \varepsilon_1,\eta_1,y_r,\dot{ y}_r,\ddot{ y}_r)$. Since sets $\Pi_0 \in {\bf R}^{3m}$ and $\Pi_1 \in {\bf R}^{2n+1}$ are compact,$\Pi_0\times\Pi_1$ is also compact. The maximum value $\bar{ B}_{1}$ of function $ B_{1}(\cdot)$ exists on $\Pi_0\times\Pi_1$ because of the continuous function property[23]. Therefore,we have
| $ \label{eq.problem-21} \dot{\varepsilon}_{1} \leq -\Gamma^{-1}_{1}\varepsilon_{1}+\bar{ B}_{1}. $ | (23) |
Consider the Lyapunov function as
| $ \label{eq.problem-22} V_{1}=\frac{1}{2} z^{\rm T}_{1} z_{1}+\frac{1}{2}\varepsilon^{\rm T}_{1}\varepsilon_{1}+\frac{1}{2\gamma_{1}}\tilde{\varsigma}^{2}_{1}, $ | (24) |
where $\gamma_{1}>0$ is a designed parameter, $\tilde{\varsigma}_{1}=\bar\varsigma_{1}-\hat{\varsigma}_{1}$,and $\dot{\tilde{\varsigma}}_{1}=-\dot{\hat{\varsigma}}_{1}$.
Differentiating (24) and considering (21) and (23),we obtain
| $ \begin{array}{*{35}{l}} {{{\dot{V}}}_{1}}\le -z_{1}^{\text{T}}{{C}_{1}}{{z}_{1}}+z_{1}^{\text{T}}{{G}_{1}}{{z}_{2}}+z_{1}^{\text{T}}{{G}_{1}}{{\varepsilon }_{1}}+z_{1}^{\text{T}}{{{\tilde{D}}}_{1}}- \\ \ \ \ \ {{{\hat{\varsigma }}}_{1}}z_{1}^{\text{T}}\text{tanh}({{z}_{1}}/{{\rho }_{1}})-\varepsilon _{1}^{T}\Gamma _{1}^{-1}{{\varepsilon }_{1}}+\varepsilon _{1}^{\text{T}}{{{\bar{B}}}_{1}}-\frac{1}{{{\gamma }_{1}}}{{{\tilde{\varsigma }}}_{1}}{{{\dot{\hat{\varsigma }}}}_{1}}\le \\ \ \ \ \ -z_{1}^{\text{T}}{{C}_{1}}{{z}_{1}}+z_{1}^{\text{T}}{{G}_{1}}{{z}_{2}}+0.5z_{1}^{\text{T}}{{G}_{1}}G_{1}^{\text{T}}{{z}_{1}}+\left\| {{z}_{1}} \right\|\left\| {{{\tilde{D}}}_{1}} \right\| \\ \ \ \ \ {{{\hat{\varsigma }}}_{1}}z_{1}^{\text{T}}\text{tanh}({{z}_{1}}/{{\rho }_{1}})-\varepsilon _{1}^{\text{T}}\Gamma _{1}^{-1}{{\varepsilon }_{1}}+\varepsilon _{1}^{\text{T}}{{\varepsilon }_{1}}+ \\ \ \ \ \ 0.5\bar{B}_{1}^{\text{T}}{{{\bar{B}}}_{1}}-\frac{1}{{{\gamma }_{1}}}{{{\tilde{\varsigma }}}_{1}}{{{\dot{\hat{\varsigma }}}}_{1}}\le \\ \ \ \ \ -({{\lambda }_{\min }}({{C}_{1}})-0.5{{{\bar{\lambda }}}_{1}})z_{1}^{\text{T}}{{z}_{1}}-({{\lambda }_{\min }}(\Gamma _{1}^{-1})-1)\varepsilon _{1}^{\text{T}}{{\varepsilon }_{1}}+ \\ \ \ \ \ z_{1}^{\text{T}}{{G}_{1}}{{z}_{2}}+\left\| {{z}_{1}} \right\|{{{\bar{\varsigma }}}_{1}}-{{{\hat{\varsigma }}}_{1}}z_{1}^{\text{T}}\text{tanh}({{z}_{1}}/{{\rho }_{1}})+ \\ \ \ \ \ 0.5\bar{B}_{1}^{\text{T}}{{{\bar{B}}}_{1}}-\frac{1}{{{\gamma }_{1}}}{{{\tilde{\varsigma }}}_{1}}{{{\dot{\hat{\varsigma }}}}_{1}}. \\ \end{array} $ | (25) |
The parameter adaptive law is chosen as
| $ \label{eq.problem-24} \dot{\hat{\varsigma}}_{1}=\gamma_{1}( z^{\rm T}_{1}{\rm tanh}( z_1/{\rho_1})-k_1\hat{\varsigma}_{1}), $ | (26) |
where $k_{1}>0$ is a designed parameter.
Substituting (26) into (25) yields
| $ \begin{array}{l} {{\dot V}_1} \le - ({\lambda _{\min }}({C_1}) - 0.5{{\bar \lambda }_1})z_1^{\rm{T}}{z_1} - ({\lambda _{\min }}(\Gamma _1^{ - 1}) - 1)\varepsilon _1^{\rm{T}}{\varepsilon _1} + \\ \;\;\;\;z_1^{\rm{T}}{G_1}{z_2} + \left\| {{z_1}} \right\|{{\bar \varsigma }_1} - {{\hat \varsigma }_1}z_1^{\rm{T}}{\rm{tanh}}({z_1}/{\rho _1}) + \\ \;\;\;\;0.5\bar B_1^{\rm{T}}{{\bar B}_1} - {{\tilde \varsigma }_1}(z_1^{\rm{T}}{\rm{tanh}}({z_1}/{\rho _1}) - {k_1}{{\hat \varsigma }_1}). \end{array} $ | (27) |
By Lemma 1,the following inequality holds:
| $ \begin{array}{l} \left\| {{z_1}} \right\|{{\bar \varsigma }_1} - {{\hat \varsigma }_1}z_1^{\rm{T}}{\rm{tanh}}({z_1}/{\rho _1}) - {{\tilde \varsigma }_1}(z_1^{\rm{T}}{\rm{tanh}}({z_1}/{\rho _1}) - {k_1}{{\hat \varsigma }_1}) = \\ \;{{\bar \varsigma }_1}(\left\| {{z_1}} \right\| - z_1^{\rm{T}}{\rm{tanh}}({z_1}/{\rho _1})) + {k_1}{{\tilde \varsigma }_1}{{\bar \varsigma }_1} - {k_1}\tilde \varsigma _1^2 \le \\ \;\; - 0.5{k_1}\tilde \varsigma _1^2 + n{\zeta _0}{\rho _1}{{\bar \varsigma }_1} + 0.5{k_1}\bar \varsigma _1^2. \end{array} $ | (28) |
Substituting (28) into (27),we have
| $ \begin{array}{l} {{\dot V}_1} \le - ({\lambda _{\min }}({C_1}) - 0.5{{\bar \lambda }_1})z_1^{\rm{T}}{z_1} - ({\lambda _{\min }}(\Gamma _1^{ - 1}) - 1)\varepsilon _1^{\rm{T}}{\varepsilon _1} + \\ \;\;\;\;z_1^{\rm{T}}{G_1}{z_2} - 0.5{k_1}\tilde \varsigma _1^2 + n{\zeta _0}{\rho _1}{{\bar \varsigma }_1} + \\ \;\;\;\;0.5{k_1}\bar \varsigma _1^2 + 0.5\bar B_1^T{{\bar B}_1}. \end{array} $ | (29) |
Step ${ i}$~${( 2\leq i \leq {k-1})\bf }$. Employ the NDO to approximate the compounded disturbance $ D_i$ which can be described as
| $ \label{eq.problem-29} \hat{ D}_{i}=\eta_{i}+ P_{i}, $ | (30) |
| $ \label{eq.problem-30} \dot{\eta}_{i}=-L_{i}\eta_{i}-L_{i}( P_{i}+ F_{i}+G_{i} x_{i+1}), $ | (31) |
where $\eta_{i}\in {\bf R}^{n}$ is the internal state of the disturbance observer,$ P_{i}\in {\bf R}^{n}$ is the designed function vector,and $L_{i}=\frac{\partial P_{i}}{\partial x_{i}} \in {\bf R}^{n\times n}$. The approximation error of the $i$-th disturbance observer is defined as
| $ \label{eq.problem-31} \tilde{ D}_{i}= D_{i}-\hat{ D}_{i}. $ | (32) |
We know that $\tilde{ D}_{i}$ is bounded according to Lemma 3, and assume that $\Vert \tilde{ D}_{i} \Vert \leq\bar{\varsigma}_{i}$.
Define
| $ \label{eq.problem-32} z_{i}= x_{i}- \alpha_{i-1} $ | (33) |
The virtual control law is designed as
| $ \label{eq.problem-33} \bar{\alpha}_{i} =G^{-1}_{i}(-C_{i} z_{i}-G^{\rm T}_{i-1} z_{i-1}- F_{i}+ \\ \ \ \ \ \dot{\alpha}_{i-1} -\hat{ D}_{i}-\hat{\varsigma}_{i}{\rm tanh}( z_i/{\rho_i})), $ | (34) |
where $C_i=C^{\rm T}_{i}>0$ and $\rho_i>0$ are designed parameters,$\hat{\varsigma}_{i}$ is the estimated value of $\bar\varsigma_{i}$,${\rm tanh}( z_i/{\rho_i})=[{\rm tanh}(z_{i,1}/{\rho_i}),{\rm tanh}(z_{i,2}/{\rho_i}),\cdots,{\rm tanh}(z_{i,n}/{\rho_i})]^{\rm T}$,and $ z_i=[z_{i,1},z_{i,2},\cdots,z_{i,n}]^{\rm T}$.
We make the virtual control law $\bar{\alpha}_i$ pass through a first-order filter,i.e.,
| $ \label{eq.problem-34} \Gamma_{i}\dot{\alpha}_i+\alpha_i=\bar{\alpha}_i,~\alpha_i(0)=\bar{\alpha}_i(0), $ | (35) |
where $\Gamma_{i}={\rm diag}\{\tau_{i,1},\tau_{i,2},\cdots,\tau_{i,n}\}$,$\tau_{i,j}>0$ is the time constant of the first-order filter,$j=1,2,\cdots,n$.
Define
| $ \label{eq.problem-35} z_{i+1}= x_{i+1}-\alpha_{i}, $ | (36) |
| $ \label{eq.problem-36} \varepsilon_i=\alpha_i - \bar{\alpha}_i. $ | (37) |
Considering (1) (32) (34) (36) and (37),the time derivative of $ z_i$ can be expressed as
| $ \label{eq.problem-37} \dot{ z}_{i} =\dot{ x}_{i}-\dot{\alpha}_{i-1} = \\ \,\,\,\, F_{i}+G_{i} z_{i+1}+G_{i} \,\,\,\,\varepsilon_{i}+G_{i}\bar{\alpha}_{i}+ D_{i}-\dot{\alpha}_{i-1}= \\ \,\,\,\,-C_{i} z_{i}+G_{i} z_{i+1}+G_{i}\varepsilon_{i}-G^{\rm T}_{i-1} z_{i-1}+ \\ \,\,\,\,\tilde{ D}_{i}-\hat{\varsigma}_{i}{\rm tanh}( z_i/{\rho_i}). $ | (38) |
Differentiating (37),we have
| $ \label{eq.problem-38} \dot{\varepsilon}_{i} =\dot{\alpha}_{i}-\dot{\bar{\alpha}}_{i} =\Gamma^{-1}_{i}(\bar{\alpha}_{i}-\alpha_{i})-\dot{\bar{\alpha}}_{i} = \\ \,\,\,\,-\Gamma^{-1}_{i}\varepsilon_i-\dot{\bar{\alpha}}_{i}\leq -\Gamma^{-1}_{i}\varepsilon_i+\bar{ B}_{i}. $ | (39) |
Consider the Lyapunov function as
| $ \label{eq.problem-39} V_{i}=\frac{1}{2} z^{\rm T}_{i} z_{i}+\frac{1}{2}\varepsilon^{\rm T}_{i}\varepsilon_{i}+\frac{1}{2\gamma_{i}}\tilde{\varsigma}^{2}_{i}, $ | (40) |
where $\gamma_{i}>0$ is a designed parameter, $\tilde{\varsigma}_{i}=\bar{\varsigma}_{i}-\hat{\varsigma}_{i}$,and $\dot{\tilde{\varsigma}}_{i}=-\dot{\hat{\varsigma}}_{i}$.
Differentiating (40) and considering (38) and (39),we obtain
| $ \label{eq.problem-40} \dot{V}_{i} \leq - z^{\rm T}_{i}C_{i} z_{i}+ z^{\rm T}_{i}G_{i} z_{i+1}+ z^{\rm T}_{i}G_{i}\varepsilon_{i}-\notag\\ \ \ \ \ \ z^{\rm T}_{i}G^{\rm T}_{i-1} z_{i-1}+ z^{\rm T}_{i}\tilde{ D}_{i}- \\ \ \ \ \ \hat{\varsigma}_{i} z^{\rm T}_{i}{\rm tanh}( z_i/{\rho_i})- \varepsilon^{T}_{i}\Gamma^{-1}_{i}\varepsilon_{i}+\varepsilon^{\rm T}_{i}\bar{ B}_{i} -\frac{1}{\gamma_{i}}\tilde{\varsigma}_{i}\dot{\hat{\varsigma}}_{i} \leq \\ \ \ \ \ (\lambda_{\min}(C_{i})-0.5\bar{\lambda}_{i}) z^{\rm T}_{i} z_{i} -(\lambda_{\min}(\Gamma^{-1}_{i})-1)\varepsilon^{\rm T}_{i}\varepsilon_{i} + \\ \ \ \ \ z^{\rm T}_{i}G_{i} z_{i+1}- z^{\rm T}_{i}G^{\rm T}_{i-1} z_{i-1}+\Vert z_{i}\Vert\bar{\varsigma}_{i} - \\ \ \ \ \ \hat{\varsigma}_{i} z^{\rm T}_{i}{\rm tanh}( z_i/{\rho_i})+0.5\bar{ B}^{\rm T}_{i}\bar{ B}_{i} -\frac{1}{\gamma_{i}}\tilde{\varsigma}_{i}\dot{\hat{\varsigma}}_{i}. $ | (41) |
The parameter adaptive law is chosen as
| $ \label{eq.problem-41} \dot{\hat{\varsigma}}_{i}=\gamma_{i}( z^{\rm T}_{i}{\rm tanh}( z_i/{\rho_i})-k_i\hat{\varsigma}_{i}), $ | (42) |
where $k_{i}>0$ is a designed parameter.
Substituting (42) into (41) and invoking Lemma 1,we obtain
| $ \label{eq.problem-42} \dot{V}_{i} \leq -(\lambda_{\min}(C_{i})-0.5\bar{\lambda}_{i}) z^{\rm T}_{i} z_{i} -(\lambda_{\min}(\Gamma^{-1}_{i})-1)\varepsilon^{\rm T}_{i}\varepsilon_{i} + \\ \ \ \ \ z^{\rm T}_{i}G_{i} z_{i+1}- z^{\rm T}_{i}G^{\rm T}_{i-1} z_{i-1}-0.5k_i\tilde{\varsigma}^{2}_{i}+ \\ \ \ \ \ n\zeta_{0}\rho_{i}\bar{\varsigma}_{i}+0.5k_{i}\bar{\varsigma}^{2}_{i}+0.5\bar{ B}^{\rm T}_{i}\bar{ B}_{i}. $ | (43) |
Step ${ k}$. Employ the NDO to approximate the compounded disturbance $ D_k$ which can be described as
| $ \label{eq.problem-43} \hat{ D}_{k}=\eta_{k}+ P_{k}, $ | (44) |
| $ \label{eq.problem-44} \dot{\eta}_{k}=-L_{k}\eta_{k}-L_{k}( P_{k}+ F_{k}+G_{k} u( v)), $ | (45) |
where $\eta_{k}\in {\bf R}^{n}$ is the internal state of the disturbance observer,$ P_{k}\in {\bf R}^{n}$ is the designed function vector,and $L_{k}=\frac{\partial P_{k}}{\partial x_{k}} \in {\bf R}^{n\times n}$. The approximation error of the $k$-th disturbance observer is defined as
| $ \label{eq.problem-45} \tilde{ D}_{k}= D_{k}-\hat{ D}_{k}. $ | (46) |
We know that $\tilde{ D}_{k}$ is bounded according to Lemma 3, and assume that $\Vert \tilde{ D}_{k} \Vert \leq\bar{\varsigma}_{k}$.
Define
| $ \label{eq.problem-46} z_{k}= x_{k}- \alpha_{k-1}. $ | (47) |
Considering (1),the time derivative of $ z_k$ can be expressed as
| $ \label{eq.problem-47} \dot{ z}_{k} =\dot{ x}_{k}-\dot{ \alpha}_{k-1}= \\ F_{k}+G_{k} u( v)+ D_{k}-\dot{\alpha}_{k-1}. $ | (48) |
Consider the Lyapunov function as
| $ \label{eq.problem-50} V_{k}=\frac{1}{2} z^{\rm T}_{k} z_{k}+\frac{1}{2\gamma_{k}}\tilde{\varsigma}^{2}_{k}, $ | (49) |
where $\gamma_{k}>0$ is a designed parameter, $\tilde{\varsigma}_{k}=\varsigma_{k}-\hat{\varsigma}_{k}$, $\hat{\varsigma}_{k}$ is the estimated value of $\bar{\varsigma}_{k}$,and $\dot{\tilde{\varsigma}}_{k}=-\dot{\hat{\varsigma}}_{k}$.
Differentiating (49) and considering (48),we obtain
| $ \label{eq.problem-51} \dot{V}_{k} = z^{\rm T}_{k} F_{k}+ z^{\rm T}_{k}G_{k} u( v)+ z^{\rm T}_{k} D_{k}- z^{\rm T}_{k}\dot{\alpha}_{k-1} -\frac{1}{\gamma_{k}}\tilde{\varsigma}_{k}\dot{\hat{\varsigma}}_{k}. $ | (50) |
The parameter adaptive law is chosen as
| $ \label{eq.problem-52} \dot{\hat{\varsigma}}_{k}=\gamma_{k}( z^{\rm T}_{k}{\rm tanh}( z_k/{\rho_k})-k_k\hat{\varsigma}_{k}), $ | (51) |
where $\rho_k>0$ and $k_{k}>0$ are the designed parameters,${\rm tanh}$ $( z_k/{\rho_k})\!\!=\!\![{\rm tanh}(z_{k,1}/{\rho_k}),{\rm tanh}(z_{k,2}/{\rho_k})\!,\!\cdots\!,\!{\rm tanh}(z_{k,n}/$ ${\rho_k})]^{\rm T}$,and $ z_k=[z_{k,1},z_{k,2},\cdots,z_{k,n}]^{\rm T}$.
Substituting (51) into (50),we obtain
| $ \label{eq.problem-53} \dot{V}_{k} = z^{\rm T}_{k} F_{k}+ z^{\rm T}_{k}G_{k} u( v)+ z^{\rm T}_{k} D_{k} - z^{\rm T}_{k}\dot{\alpha}_{k-1} -\\ \ \ \ \ \tilde{\varsigma}_{k}( z^{\rm T}_{k}{\rm tanh}( z_k/{\rho_k})-k_k\hat{\varsigma}_{k}). $ | (52) |
To eliminate the effect of the input saturation,we have the following auxiliary design system[28, 29, 30]:
| $ \label{eq.problem-200} \dot{\chi}=\left\{\begin{array}{ll} {-C_{0}\chi- \frac{1}{\Vert\chi\Vert^2}(| z^{\rm T}_{k}G_{k}\xi| +0.5\xi^{\rm T}\xi)\chi+G_{k}\xi,\Vert\chi\Vert\geq \varepsilon_{0}} \\ {0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\Vert\chi\Vert < \varepsilon_{0}} \end{array}\right. $ | (53) |
where $C_0=C^{\rm T}_{0}>0$ and $\varepsilon_0>0$ are designed parameters,and $ \xi= u( v)- v$ is the input-output difference of the actuator.
Considering the input saturation,we design the following control law:
| $ \label{eq.problem-201} v =G^{\rm T}_{k}(G_{k}G^{\rm T}_{k})^{-1}(-C_{k}( z_{k}-\chi)-G^{\rm T}_{k-1} z_{k-1}- F_{k} +\\ \ \ \ \ \dot{\alpha}_{k-1}-\hat{ D}_{k}-\hat{\varsigma}_{k}{\rm tanh}( z_k/{\rho_k})), $ | (54) |
where $C_k=C^{\rm T}_{k}>0$ is a designed matrix.
According to above analysis,the following theorem is proposed.
Theorem 1. Consider the uncertain MIMO nonlinear system (1) satisfying Assumptions 1~4. The nonlinear disturbance is given as (13),(14),(30),(31),(44) and (45),and parameter adaptive laws are chosen as (26),(42) and (51),and the auxiliary system is designed as (53). Under the control laws (17),(34) and (54),all signals of the closed-loop system are uniformly ultimately bounded.
Proof. If $\Vert\chi\Vert\geq \varepsilon_{0}$, choose the Lyapunov function as
| $ \label{eq.problem-54} V =\sum^{k}_{i=1}V_{i}=\sum^{k}_{i=1}(\frac{1}{2} z^{\rm T}_{i} z_{i}+\frac{1}{2\gamma_{i}}\tilde{\varsigma}^{2}_{i}) +\sum^{k-1}_{i=1}\frac{1}{2}\varepsilon^{\rm T}_{i}\varepsilon_{i}+\frac{1}{2}\chi^{\rm T}\chi. $ | (55) |
Considering (29) (43) (52) (53) and invoking Lemma 1, we obtain the time derivative of $V$ as follows:
| $ \label{eq.problem-55} \dot{V}\leq -\sum^{k-1}_{i=1}(\lambda_{\min}(C_i)-0.5\bar{\lambda}_{i}) z^{\rm T}_{i} z_{i} -\\ \ \ \ \ \sum^{k-1}_{i=1}(\lambda_{\min}(\Gamma^{-1}_{i})-1)\varepsilon^{\rm T}_{i}\varepsilon_{i} -\sum^{k-1}_{i=1}0.5k_{i}\tilde{\varsigma}^{2}_{i} +\\ \ \ \ \ z^{\rm T}_{k-1}G_{k-1} z_{k}+\sum^{k-1}_{i=1}(n\zeta_{0}\rho_{i}\bar{\varsigma}_{i} +0.5k_{i}\bar{\varsigma}^{2}_{i}+0.5 B^{\rm T}_{i} B_{i}) -\\ \ \ \ \ \chi^{\rm T}C_{0}\chi+ z^{\rm T}_{k} F_{k}+ z^{\rm T}_{k}G_{k} v+ z^{\rm T}_{k} D_{k} - z^{\rm T}_{k}\dot{\alpha}_{k-1} - $ $ \ \ \ \ \tilde{\varsigma}_{k}( z^{\rm T}_{k}{\rm tanh}( z_k/{\rho_k})-k_k\hat{\varsigma}_{k})-0.5\xi^{\rm T}\xi+\chi^{\rm T}G_{k}\xi \leq\\ \ \ \ \ -\sum^{k-1}_{i=1}(\lambda_{\min}(C_i)-0.5\bar{\lambda}_{i}) z^{\rm T}_{i} z_{i} -\notag\\ \ \ \ \ (\lambda_{\min}(C_k)-0.5) z^{\rm T}_{k} z_{k} -\\ \ \ \ \ \sum^{k-1}_{i=1}(\lambda_{\min}(\Gamma^{-1}_{i})-1)\varepsilon^{\rm T}_{i}\varepsilon_{i} -\sum^{k}_{i=1}0.5k_{i}\tilde{\varsigma}^{2}_{i} -\\ \ \ \ \ (\lambda_{\min}(C_0)-0.5\bar{\lambda}_{k}-0.5\lambda_{\max}(C^{\rm T}_{k}C_k))\chi^{\rm T}\chi +\\ \ \ \ \ \sum^{k}_{i=1}(n\zeta_{0}\rho_{i}\bar{\varsigma}_{i} +0.5k_{i}\bar{\varsigma}^{2}_{i})+\sum^{k-1}_{i=1}0.5 B^{\rm T}_{i} B_{i} \leq\\ \ \ \ \ -\kappa V+M, $ | (56) |
where $\kappa={\rm min}(2\lambda_{\min}(C_{i})-\bar{\lambda}_{i},2\lambda_{\min}(C_{k})-1, 2\lambda_{\min}(\Gamma^{-1}_{i})-2,k_{j}\gamma_{j}, 2\lambda_{\min}(C_0)-\bar{\lambda}_{k}-\lambda_{\max}(C^{\rm T}_{k}C_{k}))>0$,$i=1,2,\cdots,k-1$,$j=1,2,\cdots,k$,and $M=(\sum^{k}_{i=1}(n\zeta_{0}\rho_{i}\bar{\varsigma}_{i}+0.5k_i\bar{\varsigma}^{2}_{i}) +\sum^{k-1}_{i=1}0.5\bar{ B}^{\rm T}_{i}\bar{ B}_{i})>0$.
Integration of (56) yields
| $ \label{eq.problem-56} 0\leq V\leq\frac{M}{\kappa}+\left(V(0)-\frac{M}{\kappa}\right){\rm e}^{-\kappa t}. $ | (57) |
According to (57) and Lemma 2,we can obtain that all signals of the closed-loop system are uniformly ultimately bounded.
On the other hand,there does not exist input saturation in the control system if $\Vert\chi\Vert < \varepsilon_{0}$,that is, $ u( v)= v$. Under this circumstance,Theorem 1 can be easily proved with similar processes.
This concludes the proof.
Remark 2. For the auxiliary system (53),we calculate the first equation when the saturation phenomenon appears in the simulation. If $\Vert\chi\Vert < \varepsilon_{0}$ and $\xi\neq 0$,the initial value of $\chi$ is reset to eliminate the effect of input saturation.
Ⅴ. SIMULATION STUDY FOR UAVIn this section,we apply the proposed robust control scheme to the attitude tracking control of a UAV to illustrate the effectiveness. The considered attitude dynamic model of the UAV can be written as the following two MIMO nonlinear systems in accordance with singularly perturbed theory and time-scale separation principle[38]:
| $ \left\{\begin{array}{ll}\dot{\Omega}={ f_s +g_s\omega + D_s},\\ { y_s=\Omega}, \end{array}\right. $ | (58) |
| $ \left\{\begin{array}{ll}\dot{\omega}={ f_f +g_f\delta( v) + D_f},\\ { y_f=\omega}, \end{array}\right. $ | (59) |
where $\Omega=[\alpha,\beta,\mu]^{\rm T}$ is the vector of attitude angles,including angle of attack,sideslip angle and roll angle,$\omega=[p,q,r]^{\rm T}$ is the vector of attitude angular rates,including angular rate,pitch angular rate and yaw angular rate. In the slow-loop equation,$ f_s$ is the state functional vector,$g_s$ is the system matrix,$ D_s=\Delta{ f_s}+ d_s$ is the unknown compounded disturbance,$\Delta{ f_s}$ represents the system uncertainty, $ d_s$ stands for the external disturbance. In the fast-loop equation,$ f_f$ is the state functional vector, $g_f=g_{f_1}g_{f_{\delta}}$,where $g_{f_1}$ is the system matrix, $g_{f_{\delta}}$ is the allocation matrix of rudders,$ D_f=\Delta{ f_f}+ d_f$ is the unknown compounded disturbance,$\Delta{ f_f}$ represents the system uncertainty, $ d_f$ stands for the external disturbance,$ v=[v_1,v_2,v_3,v_4,v_5]^{\rm T}$ is the control input vector, $\delta( v)=[\delta_a,\delta_e,\delta_r,\delta_y,\delta_z]^{\rm T}$ denotes the plant input vector subject to saturation nonlinearity, involving ailerons,elevator,rudder,lateral deflection and longitudinal deflection of the thrust vectoring control surface. The detailed expressions of corresponding terms in (58) and (59) can be found in [38].
The initial conditions for the UAV are chosen as $\alpha_0 = 2^{\circ}$,$\beta_0=1^{\circ}$,$\mu_0=0^{\circ}$, $p_0=q_0=r_0=0\,{\rm rad/s}$, $\delta_{aM}=\delta_{eM}=\delta_{rM}=30^{\circ}$,and $\delta_{yM}=\delta_{zM}=15^{\circ}$. The desired attitudes are chosen as
| $ \label{eq.problem-65} \alpha_c=\ (3+2\sin(0.2\pi t)+\cos(0.1\pi t))^{\circ},\\ ~\beta_c=\ \left\{\begin{array}{ll}{0^{\circ},~~4k\leq{t}<4(k+1)} \\ {16^{\circ},~4(k+1)\leq {t}<4(k+2)}\end{array}\right.,\,k=0,2,4,\cdots,\\ \mu_c=\ 10^{\circ}. $ | (60) |
Suppose that there are $+30\%$ and $-30\%$ uncertainties on aerodynamic coefficients and aerodynamic moment coefficients, respectively. On the other hand,the unknown time-varying disturbance moments in the fast-loop system of the UAV are given by
| $ \label{eq.problem-66} d_{Mf}(t) = \left[\begin{array}{cccccc} {5\times 10^{6}(\sin(5t)+0.5)} \\ {6 \times 10^{6}(\cos(5t))} \\ {6 \times 10^{6}(\sin(5t)+0.3)} \end{array}\right] {\rm N\cdot m}. $ | (61) |
The designed parameters of the proposed robust adaptive tracking control scheme are chosen as $ P_{1}=[2\alpha+0.5,2\beta+0.5,2\mu+0.5]^{\rm T}$,$C_{1}={\rm diag}\{4,4,4\}$,$\rho_1=0.4$,$\gamma_1=0.5$,$k_1=0.2$, $\Gamma_{1}={\rm diag}\{0.02,0.02,0.02\}$,$ P_{2}=[2p+0.5,2q+0.5,2r+0.5]^{\rm T}$,$C_{2}={\rm diag}\{2.5,2.5,2.5\}$,$\rho_2=2.5$,$\gamma_2=1.0$,$k_2=0.5$, $C_{0}={\rm diag}\{5,5,5\}$,and $\varepsilon_{0}=0.02$.
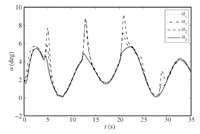
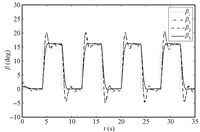
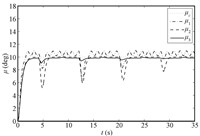
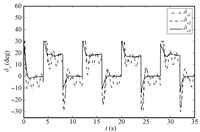
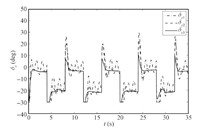
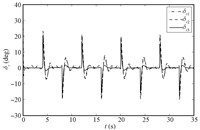
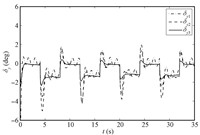
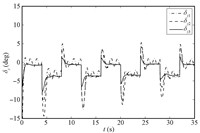
The simulation results are shown in Figs. 1~8,where dot lines (with subscript "c") represent the desired attitudes,and dash dot lines (with subscript "1") stand for the responses without NDO or saturation compensation,and dash lines (with subscript "2") represent the responses with NDO,and solid lines (with subscript "3") stand for the responses with NDO and saturation compensation.
|
Download:
|
| Fig. 1. Angle of attack. | |
|
Download:
|
| Fig. 2. Sideslip angle. | |
|
Download:
|
| Fig. 3. Roll angle. | |
|
Download:
|
| Fig. 4. Ailerons. | |
|
Download:
|
| Fig. 5. Elevator. | |
|
Download:
|
| Fig. 6. Rudder. | |
|
Download:
|
| Fig. 7. Lateral defection of the thrust vectoring control surface. | |
|
Download:
|
| Fig. 8. Longitudinal deflection of the thrust vectoring control surface. | |
Under the proposed robust adaptive tracking control scheme based on the backstepping approach,DSC and NDO,we can see that the system outputs follow the desired values in a satisfactory way in the presence of system uncertainty,unknown external disturbance,and input saturation from Figs. 1~3. The compounded disturbance can be well tackled with NDO,and the oscillation phenomena is reduced. On the other hand,the control inputs are presented in Figs. 4~8. It should be noticed that the designed auxiliary system can make actuators drop out the saturation nonlinearity gradually,eliminating the effect of input saturation. Based on above simulation results and stated analysis,the proposed robust adaptive tracking control strategy is valid for uncertain MIMO nonlinear systems with system uncertainty,unknown external disturbance,and input saturation.
Ⅵ. CONCLUSIONAn effective robust adaptive tracking control scheme is proposed for uncertain MIMO nonlinear systems in the presence of system uncertainty,unknown external disturbance,and input saturation based on the backstepping technique and the NDO. To eliminate the effect of input saturation,an auxiliary system is constructed. The dynamic surface method is employed to deal with the explosion of complexity in backstepping control. It is proved that all signals of the closed-loop system based on the proposed robust adaptive tracking control scheme are uniformly ultimately bounded through Lyapunov stability analysis. Finally,the developed control strategy is applied to the attitude tracking control of a UAV,and simulation results show that the proposed robust control scheme is effective.
| [1] | Chen M, Jiang B, Wu Q X, Jiang C S. Robust control of near-space vehicles with input backslash-like hysteresis. Proceedings of the Institutior of Mechanical Engineers, Part I:Journal of Systems and Control Engineering, 2013, 227(8):635-644 |
| [2] | Ji Chen-Xin. Key technology and application of military unmanned aerial vehicles. Modern Defence Technology, 2009, 37(6):26-30(in Chinese) |
| [3] | Wang Qin, Ye Yun-Qing. Application of unmanned aerial vehicle in navy. Command Information System and Technology, 2012, 3(4):36-40(in Chinese) |
| [4] | Wang F, Cui J Q, Chen B M, Lee T H. A comprehensive UAV indoor navigation system based on vision optical flow and laser fastslam. Acta Automatic Sinica, 2013, 39(11):1889-1990 |
| [5] | Kang Y, Hedrick J K. Linear tracking for a fixed-wing UAV using nonlinear model predictive control. IEEE Transactions on Control Systems Technology, 2009, 17(5):1202-1210 |
| [6] | Dierks T, Jagannathan S. Output feedback control of a quadrotor UAV using neural networks. IEEE Transactions on Neural Networks, 2010, 21(1):50-66 |
| [7] | Nodland D, Zargarzadeh H, Jagannathan S. Neural network-based optimal adaptive output feedback control of a helicopter UAV. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(7):1061-1073 |
| [8] | Chen M, Mei R, Jiang B. Sliding mode control for a class of uncertain MIMO nonlinear systems with application to near-space vehicles. Mathematical Problems in Engineering, 2013, DOI:10.1155/2013/180589 |
| [9] | Dydek Z T, Annaswamy A M, Lavretsky E. Adaptive control of quadrotor UAVs:a design trade study with flight evaluations. IEEE Transactions on Control Systems Technology, 2013, 21(4):1400-1406 |
| [10] | Chen W H, Ballance D J, Gawthrop P J, O0Reilly J. A nonlinear disturbance observer for robotic manipulators. IEEE Transactions on Industrial Electronics, 2000, 47(4):932-938 |
| [11] | Chen W H. Nonlinear disturbance observer-enhanced dynamic inversion control of missiles. Journal of Guidance, Control, and Dynamics, 2003, 26(1):161-166 |
| [12] | Chen M, Chen W H. Sliding mode control for a class of uncertain nonlinear systems based on disturbance observer. International Journal of Adaptive Control and Signal Processing, 2010, 24(1):51-64 |
| [13] | Qian C S, Sun C Y, Huang Y Q, Mu C X, Zhang J M, Zhang R M. Design of flight control system for a hypersonic gliding vehicle based on nonlinear disturbance observer. In:Proceedings of the 10th IEEE International Conference on Control and Automation. Hangzhou, China:IEEE, 2013. 1573-1577 |
| [14] | Pu Ming, Wu Qing-Xian, Jiang Chang-Sheng, Cheng Lu. Application of adaptive second-order dynamic terminal sliding mode control to near space vehicle. Journal of Aerospace Power, 2010, 25(5):1169-1176(in Chinese) |
| [15] | Guo Tao, Wang Ding-Lei, Wang Ai-Min. Adaptive backstepping control for constrained systems using nonlinear mapping. Acta Automatic Sinica, 2013, 39(9):1558-1563(in Chinese) |
| [16] | Cui R X, Ren B B, Ge S S. Synchronised tracking control of multi-agent system with high-order dynamics. IET Control Theory and Applications, 2012, 6(5):603-614 |
| [17] | Wang H Q, Chen B, Lin C. Adaptive neural tracking control for a class of perturbed pure-feedback nonlinear systems. Nonlinear Dynamics, 2013, 72(1-2):207-220 |
| [18] | Li T S, Li R H, Wang D. Adaptive neural control of nonlinear MIMO systems with unknown time delays. Neurocomputing, 2012, 78(1):83-88 |
| [19] | Li Y M, Tong S C, Li T S. Adaptive fuzzy output feedback control of MIMO nonlinear uncertain systems with time-varying delays and unknown backlash-like hysteresis. Neurocomputing, 2012, 93:56-66 |
| [20] | Swaroop D, Hedrick J K, Yip P P, Gerdes J C. Dynamic surface control for a class of nonlinear systems. IEEE Transactions on Automatic Control, 2000, 45(10):1893-1899 |
| [21] | Li Tie-Shan, Zou Zao-Jian, Luo Wei-Lin. DSC-backstepping based robust adaptive NN control for nonlinear systems. Acta Automatica Sinica, 2008, 34(11):1424-1430(in Chinese) |
| [22] | Xu Y Y, Tong S C, Li Y M. Adaptive fuzzy fault-tolerant decentralized control for uncertain nonlinear large-scale systems based on dynamic surface control technique. Journal of the Franklin Institute, 2014, 351(1):456-472 |
| [23] | Li T S, Zhang H Y, Yang X Y. DSC approach to robust adaptive fuzzy tracking control for strict-feedback nonlinear systems. In:Proceedings of the 5th International Conference on Fuzzy Systems and Knowledge Discovery. Jinan, China:IEEE, 2008. 70-74 |
| [24] | Jia Tao, Liu Jun, Qian Fu-Cai. Adaptive fuzzy dynamic surface control for a class of nonlinear systems with unknown time-delays. Acta Automatica Sinica, 2011, 37(1):83-91(in Chinese) |
| [25] | Wen C Y, Zhou J, Liu Z T, Su H Y. Robust adaptive of uncertain nonlinear systems in the presence of input saturation and external disturbance. IEEE Transactions on Automatic Control, 2011, 56(7):1672-1678 |
| [26] | Li Y M, Tong S C, Li T S. Direct adaptive fuzzy backstepping control of uncertain nonlinear systems in the presence of input saturation. Neural Computing and Applications, 2013, 23(5):1207-1216 |
| [27] | Zhou Yan-Long, Chen Mou. Robust control of nonlinear systems with input constraint based on disturbance observer. Journal of Nanjing University of Science and Technology, 2014, 38(1):40-47(in Chinese) |
| [28] | Chen M, Ge S S, Ren B B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints. Automatica, 2011, 47(3):452-465 |
| [29] | Chen M, Ge S S, How B V E. Robust adaptive neural network control for a class of uncertain MIMO nonlinear systems with input nonlinearities. IEEE Transactions on Neural Networks, 2010, 21(5):796-812 |
| [30] | Chen M, Ge S S, Choo Y S. Neural network tracking control of ocean surface vessels with input saturation. In:Proceedings of the 2009 IEEE International Conference on Automation and Logistics. Shenyang, China:IEEE, 2009. 85-89 |
| [31] | Kurtz M J, Henson M A. Input-output linearizing control of constrained nonlinear processes. Journal of Process Control, 1997, 7(1):3-17 |
| [32] | Kong Xiao-Bin, Liu Xiang-Jie. Continuous-time nonlinear model predictive control with input/output linearization. Control Theory and Applications, 2012, 29(2):217-224(in Chinese) |
| [33] | Liu D R, Wang D, Yang X. An iterative adaptive dynamic programming algorithm for optimal control of unknown discrete-time nonlinear systems with constrained inputs. Information Sciences, 2013, 220:331-342 |
| [34] | Wang D, Liu D R, Zhao D B, Huang Y Z, Zhang D H. A neuralnetwork-based iterative GDHP approach for solving a class of nonlinear optimal control problems with control constraints. Neural Computing and Applications, 2013, 22(2):219-227 |
| [35] | Chen M, Jiang B. Robust attitude control of near space vehicles with time-varying disturbances. International Journal of Control, Automation, and Systems, 2013, 11(1):182-187 |
| [36] | Polycarpou M M. Stable adaptive neural control scheme for nonlinear systems. IEEE Transactions on Automatic Control, 1996, 41(3):447-451 |
| [37] | Tee K P, Ge S S. Control of fully actuated ocean surface vessels using a class of feedforward approximators. IEEE Transactions on Control Systems Technology, 2006, 14(4):750-756 |
| [38] | Pang J, Mei R, Chen M. Modeling and control for near space vehicles with oblique wing. In:Proceedings of the 10th World Congress on Intelligent Control and Automation. Beijing, China:IEEE, 2012. 1773-1778 |
 2015, Vol.2
2015, Vol.2 


