COMPARED with the fixed-wing unmanned aerial vehicles (UAVs),unmanned helicopters have the characters of hovering,autonomous take-off and landing vertically and multi-attitude flight. They have a wide application prospect in the field of military and civilian applications. The unmanned helicopter is a special controlled object,which is a dynamic system of 6-degree-of-freedom (DOF),underactuated,multi-input multi-output (MIMO),strong coupling and nonlinear. Consequently, the development of sophisticated and reliable unmanned helicopter flight control system has recently become an attractive research topic in academic communities worldwide[1].
Nowadays,unmanned helicopter control methods include linear controller,nonlinear controller and intelligent controller. Traditional approaches to flight control and most initial attempts to achieve autonomous helicopter flight have been developed based on linear design techniques such as proportional-integral-derivative(PID)[2],linear quadratic regulator (LQR)[3],$H_{\infty }$[4] and gain scheduling[5]. Linear control method is effective when the dynamic system state of an unmanned helicopter is near the equilibrium point. However,when the helicopter is away from the equilibrium point or aerobatic maneuvers are performed,the performance of the control system will deteriorate greatly. Therefore,in recently years there have been a growing number of papers using nonlinear control methods to deal with unmanned helicopter flight control. It is shown in [6] that approximated unmanned helicopter system with dynamic decoupling is full state linearizable by choosing positions and heading as outputs. Nonlinear backstepping trajectory tracking control design for small scale helicopters is presented in [7]. A two-time scale controller is presented in [8] by using adaptive backstepping technique to achieve the hover flight control of an unmanned helicopter. Robust trajectory tracking control design for unmanned helicopters is introduced in [9, 10]. A position tracking control system for a UAV using robust integral of the signum of error (RISE) and neural network (NN) feedforward terms is developed in [11]. In addition to the above two methods,intelligent control has also been widely used in the autonomous control of unmanned helicopters. The control methods based on model-free fuzzy and neural networks are reported in [12, 13] respectively for their successful applications to autonomous flight control.
This paper presents an adaptive backstepping control design for unmanned helicopters with parametric uncertainties. The proposed controller employs online parameter update laws to estimate unknown parameters associated with the helicopter$'$s dynamics of mass and moment coefficients. When parametric uncertainties exist in the dynamic model,the proposed controller will be a significant improvement to the traditional exact model knowledge (EMK) control method as employed in [6, 7]. We use a simplified unmanned helicopter$'$s nonlinear dynamic model for the flight control development. The main objective is to let the unmanned helicopter track a predefined position and heading reference trajectory. In order to facilitate the control design,we divide the helicopter model into three subsystems,which are the altitude subsystem,the yaw subsystem and the horizontal subsystem. Since there is no strong coupling between the three subsystems,we can design the controllers separately. The proposed design approach is obviously different from the two-level hierarchical control scheme reported in [8, 11]. It is reasonable in that this approach is mathematically consistent with the intuitive flight notion. The global asymptotical stability (GAS) of the closed-loop error system is proved by a Lyapunov based stability analysis. Numerical simulations demonstrate that the proposed controller can achieve good tracking performance in the presence of parametric uncertainties.
This paper is organized as follows. In the next section,the nonlinear dynamic model of the unmanned helicopter is introduced. Sections III and IV are the main body of this paper,which present the adaptive backstepping control design and the stability analysis method. Simulation results and conclusion are presented in Sections V and VI.
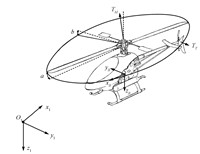
Ⅱ. DYNAMIC MODEL OF THE HELICOPTERIn order to develop the helicopter$'$s equations of motion,first of all we should define two reference frames. The first one is the inertia frame defined as $\mathcal{F}_{I}=\left\{ O_{I},\vec{x}_{I},\vec{y}_{I},\vec{z}_{I}\right\} $. The second is the body fixed reference frame defined as $\mathcal{F}_{B}=\left\{ O_{B},\vec{x}_{B},\vec{y}_{B},\vec{z}_{B}\right\} $,where the center $O_{B}$ is located at the center of gravity (CG) of the unmanned helicopter. The direction of the inertia frame and the body frame unitary vectors can be seen in Fig. 1. For the purpose of control,we consider a complete helicopter model as a rigid body with a force and moment generation process. The dynamic equations of the helicopter$'$s rigid body can be derived using Newton-Euler equations in the configuration space $SE(3)={{\mathbf{R}}^{3}}\times SO(3)$[6, 9, 14]. There are four control inputs associated with helicopter piloting,which are defined as $u=\left[ \begin{array}{cccc} T_{M} & T_{T} & a & b% \end{array}% \right] ^{\rm T}$. The former two components $T_{M}$ and $T_{T}$ are the magnitudes of the thrusts generated by the main and tail rotors. The latter two control commands are the flapping angles $a$,$b$,which represent the tilts of the tip-path-plane (TPP) at the longitudinal and lateral axes,respectively. The four control inputs are also depicted in Fig. 1. In the following,we will give the unmanned helicopter$'$s translational and rotational dynamics,respectively. More details can be found in [6, 7, 10].
|
Download:
|
| Fig.1. Coordinate systems for the helicopter. | |
The kinematic and dynamic equations of unmanned helicopter$'$s translational motion with respect to the inertial frame can be described as
| \begin{equation} \begin{array}{ccc} \dot{p}^{I}=v^{I},& & m\dot{v}^{I}=-Re_{3}T_{M}+mge_{3}, \end{array} \label{translationaldynamics} \end{equation} | (1) |
where $p^{I}=\left[ \begin{array}{ccc} p_{x}^{I} & p_{y}^{I} & p_{z}^{I}% \end{array}% \right] ^{\rm T}\in {\bf R}^{3}$ represents the position vector of the CG of the helicopter with respect to the inertial coordinates, $v^{I}=\left[ \begin{array}{ccc} v_{x}^{I} & v_{y}^{I} & v_{z}^{I}% \end{array}% \right] ^{\rm T}\in {\bf R}^{3}$ represents the linear velocity vector in the inertial coordinates,$m$ is the mass of the helicopter,$e_{3}=\left[ \begin{array}{ccc} 0 & 0 & 1% \end{array}% \right] ^{\rm T}$,the rotation matrix $R$ is parameterized with respect to the three Euler angles roll $(\phi )$,pitch $(\theta )$ and yaw $(\psi )$ and maps vectors from the body fixed frame $\mathcal{F}_{B}$ to the inertial frame $\mathcal{F}_{I}$,which is given by
| \begin{equation} R\!=\!\left[\!\! \begin{array}{ccc} C_{\psi }C_{\theta } & -S_{\psi }C_{\phi }+C_{\psi }S_{\theta }S_{\phi } & S_{\phi }S_{\psi }+C_{\phi }S_{\theta }C_{\psi } \\ S_{\psi }C_{\theta } & C_{\phi }C_{\psi }+S_{\phi }S_{\theta }S_{\psi } & -C_{\psi }S_{\phi }+S_{\psi }S_{\theta }C_{\phi } \\ -S_{\theta } & C_{\theta }S_{\phi } & C_{\theta }C_{\phi }% \end{array}\!\! \right]. \end{equation} | (2) |
Hereafter the abbreviations $C_{\cdot }$,$S_{\cdot }$ and $T_{\cdot }$ represent the trigonometric functions ${\rm cos}\left( \cdot \right) $,${\rm sin}\left( \cdot \right) $ and ${\rm tan}\left( \cdot \right),$ respectively.
B. Rotational DynamicsThe kinematic and dynamic equations of unmanned helicopter$'$s rotational motion with respect to the body fixed framework can be described as
| \begin{equation} \begin{array}{c} \begin{array}{ccc} \dot{\Theta}=\Psi (\Theta )\omega ^{B},& & \dot{R}=RS\left( \omega ^{B}\right),\end{array}\\\\ J\dot{\omega}^{B}=-S\left( \omega ^{B}\right) J\omega ^{B}+A\left( T_{M}\right) v_{c}+B\left( T_{M}\right), \end{array} \label{rotationaldynamics} \end{equation} | (3) |
where $\Theta =\left[ \begin{array}{ccc} \phi & \theta & \psi \end{array}% \right] ^{\rm T}\in {\bf R}^{3}$ represents the Euler angles, $\omega ^{B}=\left[ \begin{array}{ccc} \omega _{x} & \omega _{y} & \omega _{z}% \end{array}% \right] ^{\rm T}\in {\bf R}^{3}$ represents angular velocity vector with respect to the body frame. Angular velocity transfer matrix in (3) is given by
| \begin{equation} \Psi (\Theta )=\left[ \begin{array}{ccc} 1 & S_{\phi }T_{\theta } & C_{\phi }T_{\theta } \\ 0 & C_{\phi } & -S_{\phi } \\ 0 & \frac{S_{\phi }}{C_{\theta }} & \frac{C_{\phi }}{C_{\theta }}% \end{array}% \right], \end{equation} | (4) |
$S\left( \omega^{B} \right) $ in (3) denotes a skew symmetric matrix,which is given by
| \begin{equation} S\left( \omega^{B}\right) =\left[ \begin{array}{ccc} 0 & -\omega _{z} & \omega _{y} \\ \omega _{z} & 0 & -\omega _{x} \\ -\omega _{y} & \omega _{x} & 0% \end{array}% \right], \end{equation} | (5) |
$J$ in (3) denotes the inertia matrix of the helicopter with respect to the body frame,which can be expressed as
| \begin{equation} J=\left[ \begin{array}{ccc} J_{xx} & 0 & 0 \\ 0 & J_{yy} & 0 \\ 0 & 0 & J_{zz}% \end{array}% \right], \end{equation} | (6) |
$v_{c}=\left[ \begin{array}{ccc} b & a & T_{T}% \end{array}% \right] ^{\rm T}$,$A(T_{M})\in {\bf R}^{3\times 3}$ represents an invertible matrix for $T_{M}$,$B(T_{M})\in {\bf R}^{3}$ represents a parameter vector for $T_{M}$.
C. Control ObjectiveWhen the unmanned helicopter is in operation,load changes and other factors may cause the parametric uncertainties in the system dynamics. It will greatly affect the performance of conventional control method based on EMK. Thus the proposed controller combines the backstepping method with online parameter update laws to achieve the control objective. The main control objective is to design the four control inputs $u=\left[ \begin{array}{cccc} T_{M} & T_{T} & a & b% \end{array}% \right] ^{\rm T}$ in order to asymptotically track the reference trajectories of $x_{r}(t)$,$y_{r}(t)$,$z_{r}(t)$ and $\psi _{r}(t)$ subject to model uncertainties of mass and moment coefficient. The components of $x_{r}(t)$ and $y_{r}(t)$ are required to be $C^{4}$ functions of time,$z_{r}(t)$ and $\psi _{r}(t)$ are required to be $C^{2}$ functions of time.
To deal with the subsequent control development,we make some assumptions as follows:
Assumption 1. $\left\vert \theta \left( t\right) \right\vert <\frac{\pi }{2}$ and $\left\vert \phi \left( t\right) \right\vert <\frac{\pi }{2}$ for $t\geq 0$.
Assumption 2. $T_{M}>0$ for $t\geq 0$.
The purpose of Assumption 1 is to assure the control input $T_{M}$ which will be designed in the following is non-singular. Obviously, this assumption is necessary to avoid singularities in angular velocity transfer matrix of (4). Similar assumption was applied in [7]. The purpose of Assumption 2 is to assure the pseudo control $r_{d}$ which will be designed in the following is non-singular. Similar assumption was employed in [9].
Ⅲ. FLIGHT CONTROL DESIGNIn order to achieve the control objective,the proposed controller follows adaptive backstepping design principles[15]. For the purpose of improving the autonomous flight performance,we employ adaptive backstepping technique to deal with the parametric uncertainties by using online parameter estimation laws. In this paper,we divide the helicopter$'$s dynamic model into three subsystems,which are the altitude subsystem,yaw subsystem and horizontal subsystem. Since there is no strong coupling between these subsystems,the controller for each subsystem can be developed separately.
A. Altitude SubsystemBy elaborating (1),the vertical dynamics are described as
| \begin{equation} \begin{array}{ccc} \dot{p}_{z}^{I}=v_{z}^{I},& & \dot{v}_{z}^{I}=-\frac{1}{m}\rho _{33}T_{M}+g, \end{array} \label{altitudeerror} \end{equation} | (7) |
where $\rho _{ij}$ denotes the element of $jth$ row and $ith$ column of the rotation matrix $R$.
Step 1. Let the altitude and vertical velocity tracking errors be defined as
| \begin{equation} \begin{array}{ccc} e_{pz}=z_{r}-p_{z}^{I},& & e_{vz}=v_{zd}^{I}-v_{z}^{I}, \end{array} \label{altitudetrackingerror} \end{equation} | (8) |
where $v_{zd}^{I}$ denotes the vertical velocity virtual control. By taking the time derivative of $e_{pz}$,the open-loop altitude tracking error dynamics can be obtained as follows:
| \begin{equation} \dot{e}_{pz}=\dot{z}_{r}-v_{zd}^{I}+e_{vz}. \label{openloopaltitudeerrordynamics} \end{equation} | (9) |
Let the virtual control signal $v_{zd}^{I}$ be designed as
| \begin{equation} v_{zd}^{I}=\dot{z}_{r}+k_{1}e_{pz}, \end{equation} | (10) |
where $k_{1}\in {\bf R}$ is a positive,constant control gain. Then the closed-loop altitude tracking error dynamics will take the following form
| \begin{equation} \dot{e}_{pz}=-k_{1}e_{pz}+e_{vz}. \end{equation} | (11) |
Step 2. By taking the time derivative of $e_{vz}$,the open-loop vertical velocity tracking error dynamics can be written as follows:
| \begin{equation} m\dot{e}_{vz}=m\dot{v}_{zd}^{I}-mg+\rho _{33}T_{M}. \end{equation} | (12) |
On account of the mass uncertainty in the error dynamics,in this step we use the adaptive control law to estimate the unknown parameter on line. In order to facilitate the subsequent analysis, we make some changes to the corresponding terms of the right side of (12) as follows:
| \begin{equation} \begin{array}{ccc} m\dot{v}_{zd}^{I}-mg=Y_{1}(\dot{v}_{zd}^{I})\eta _{1},& & -\rho _{33}T_{M}=U, \end{array} \label{rightside1} \end{equation} | (13) |
where $\eta _{1}\in {\bf R}$ represents the unknown mass of the helicopter. According to (13),we know that the unknown parameter satisfies the condition of linear parameterization (LP). Thus,the open-loop vertical velocity tracking error dynamics can be revised into the following advantageous form
| \begin{equation} m\dot{e}_{vz}=Y_{1}(\dot{v}_{zd}^{I})\eta _{1}-U. \end{equation} | (14) |
Here we design the general control input $U$ as follows:
| \begin{equation} U=Y_{1}(\dot{v}_{zd}^{I})\hat{\eta}_{1}+k_{2}e_{vz}+e_{pz}, \end{equation} | (15) |
where $k_{2}\in {\bf R}$ is a positive,constant control gain, $\hat{\eta}_{1}$ is the online estimation of unknown parameter $\eta_{1}$. After combining (13) with (15),the real control input $T_{M}$ can be derived as follows:
| \begin{equation} T_{M}=-\frac{U}{\rho _{33}}=-\frac{Y_{1}(\dot{v}_{zd}^{I})\hat{\eta}% _{1}+k_{2}e_{vz}+e_{pz}}{C_{\theta }C_{\phi }}. \end{equation} | (16) |
The adaptive updating law of unknown parameter can be designed as follows:
| \begin{equation} \dot{\hat{\eta}}_{1}=\gamma _{1}Y_{1}(\dot{v}_{zd}^{I})e_{vz}, \end{equation} | (17) |
where $\gamma _{1}\in {\bf R}$ is a positive,constant adaptation gain. Substituting (15) into (14),we can derive the closed-loop vertical velocity tracking error dynamics as follows:
| \begin{equation} m\dot{e}_{vz}=Y_{1}(\dot{v}_{zd}^{I})\tilde{\eta}_{1}-k_{2}e_{vz}-e_{pz}, \end{equation} | (18) |
where $\tilde{\eta}_{1}=\eta _{1}-\hat{\eta}_{1}\in {\bf R}$ denotes the unknown parameter estimation error.
In order to facilitate the subsequent system stability analysis, we define a Lyapunov function candidate,denoted by $V_{1}(t)\in {\bf R}$,as follows:
| \begin{equation} V_{1}=\frac{1}{2}e_{pz}^{2}+\frac{1}{2}me_{vz}^{2}+\frac{1}{2}\gamma _{1}^{-1}\tilde{\eta}_{1}^{2}\geq 0. \end{equation} | (19) |
By taking the time derivative of (19) and making the appropriate substitutions from (11),(17) and (18),we derive the following expression
| \begin{equation} \dot{V}_{1}=-k_{1}e_{pz}^{2}-k_{2}e_{vz}^{2}. \end{equation} | (20) |
| \begin{equation} \dot{\psi}=\Psi _{3}\left( \Theta \right) \omega ^{B}, \end{equation} | (21) |
where $\Psi _{3}\left( \Theta \right) $ is the third row of matrix $\Psi (\Theta )$ defined in (4).
Step 3. Let the yaw angular and yaw angular velocity tracking error be defined as
| \begin{equation} \begin{array}{ccc} e_{\psi }=\psi _{r}-\psi,& & e_{\omega z}=\omega _{zd}-\omega _{z}, \end{array} \label{yawdynamics} \end{equation} | (22) |
where $\omega _{zd}$ represents the yaw angular velocity virtual control. By taking the time derivative of $e_{\psi}$,we can derive the open-loop yaw error dynamics as follows:
| \begin{equation} \dot{e}_{\psi }=\dot{\psi}_{r}-\frac{S_{\phi }}{C_{\theta }}\omega _{y}-% \frac{C_{\phi }}{C_{\theta }}\omega _{zd}+\epsilon \left( \phi ,\theta \right) e_{\omega }, \end{equation} | (23) |
where $\epsilon \left( \phi ,\theta \right) =\left[ \begin{array}{ccc} 0 & 0 & \frac{C_{\phi }}{C_{\theta }}% \end{array}% \right] $. In order to cancel out the nonlinear terms and stabilize the yaw error dynamics,we choose the virtual control input as follows:
| \begin{equation} \omega _{zd}=\frac{C_{\theta }}{C_{\phi }}\left[\dot{\psi}_{r}-\frac{% S_{\phi }}{C_{\theta }}\omega _{y}+\lambda _{\psi}e_{\psi }\right], \end{equation} | (24) |
where $\lambda _{\psi}\in {\bf R}$ is a positive,constant control gain. Substituting (24) into (23),we can get the closed-loop yaw error dynamics as follows:
| \begin{equation} \dot{e}_{\psi }=-\lambda _{\psi}e_{\psi }+\epsilon \left( \phi ,\theta \right) e_{\omega }. \end{equation} | (25) |
We define a Lyapunov function candidate for this subsystem, denoted by $V_{2}(t)\in {\bf R}$,as follows:
| \begin{equation} V_{2}=\frac{1}{2}e_{\psi }^{2}. \end{equation} | (26) |
By take the time derivative of (26) and making the substitution from (25),we can derive the following equation:
| \begin{equation} \dot{V}_{2}=-\lambda _{\psi}e_{\psi }^{2}+e_{\psi }\epsilon \left( \phi ,\theta \right) e_{\omega } . \end{equation} | (27) |
Since the lateral-longitudinal dynamics has strong coupling with the attitude dynamics,we focus our attention on a cascade control structure constituted by an inner-loop controlling the attitude dynamics and a outer-loop governing the lateral-longitudinal dynamics. In the following paragraphs,the proposed controller uses the adaptive backstepping design principles to deal with the horizontal subsystem with parametric uncertainties,which can be described in a parametric-pure-feedback form[15].
The dynamics of the horizontal subsystem,after elaborating (1) and (3),can be explicitly described as follows:
| \begin{equation} \begin{array}{c} \begin{array}{ccccc} \dot{p}_{1}=v_{1},& & \dot{v}_{1}=-\frac{1}{m}rT_{M},& & \dot{r}=\Pi \omega _{1}, \end{array} \\ \\ J\dot{\omega}^{B}=-S\left( \omega ^{B}\right) J\omega ^{B}+A\left( T_{M}\right) v_{c}+B\left( T_{M}\right), \end{array} \label{horizontaldynamics} \end{equation} | (28) |
where
| $p_{1}=\left[ \begin{array}{cc} p_{x}^{I} & p_{y}^{I}% \end{array}% \right] ^{\rm T}$,$v_{1}=\left[ \begin{array}{cc} v_{x}^{I} & v_{y}^{I}% \end{array}% \right] ^{\rm T}$,$r=\left[ \begin{array}{cc} \rho _{31} & \rho _{32}% \end{array}% \right] ^{\rm T}$,$\omega _{1}=\left[ \begin{array}{cc} \omega _{x} & \omega _{y}% \end{array}% \right] ^{\rm T}$,$\Pi =\left[ \begin{array}{cc} -\rho _{21} & \rho _{11} \\ -\rho _{22} & \rho _{12}% \end{array}% \right] $. |
Step 4. Let the horizontal position and horizontal velocity tracking errors be defined as
| \begin{equation} \begin{array}{ccc} e_{p1}=p_{1r}-p_{1},& & e_{v1}=v_{1d}-v_{1}, \end{array} \label{horizontalerror} \end{equation} | (29) |
where $p_{1r}=\left[ \begin{array}{cc} x_{r} & y_{r}% \end{array}% \right] ^{\rm T}\in {\bf R}^{2}$,$v_{1d}$ represents the desired horizontal velocity. By taking the time derivative of $e_{p1}$,we can derive the open-loop horizontal position tracking error dynamics as follows:
| \begin{equation} \dot{e}_{p1}=\dot{p}_{1r}-v_{1d}+e_{v1}. \end{equation} | (30) |
| \begin{equation} v_{1d}=\dot{p}_{1r}+K_{3}e_{p1}, \end{equation} | (31) |
| \begin{equation} \dot{e}_{p1}=-K_{3}e_{p1}+e_{v1}. \end{equation} | (32) |
Step 5. By taking the time derivative of $e_{v1}$,the open-loop horizontal velocity tracking error dynamics can be written as follows:
| \begin{equation} m\dot{e}_{v1}=m\dot{v}_{1d}+rT_{M}. \end{equation} | (33) |
The corresponding term of the right-hand side of the dynamics equation (33),which includes the unknown parameter,can be linearly parameterized as
| \begin{equation} m\dot{v}_{1d}=Y_{2}\left( \dot{v}_{1d}\right) \eta _{2}, \end{equation} | (34) |
where $\eta _{2}\in {\bf R}$ represents the unknown mass of the helicopter. Thus,the error dynamics of (33) can be changed to
| \begin{equation} m\dot{e}_{v1}=Y_{2}\left( \dot{v}_{1d}\right) \eta _{2}+rT_{M}. \end{equation} | (35) |
In this step,we take $r_{d}$ as the desired direction of the thrust vector,and define the orientation error as
| \begin{equation} e_{r}=r_{d}-r. \end{equation} | (36) |
Substituting (36) into (35),we can rewrite the open-loop horizontal velocity tracking error dynamics in the following form:
| \begin{equation} m\dot{e}_{v1}=Y_{2}\left( \dot{v}_{1d}\right) \eta _{2}+r_{d}T_{M}-e_{r}T_{M}. \end{equation} | (37) |
Here we design the orientation virtual control as follows:
| \begin{equation} r_{d}=\frac{1}{T_{M}}\left[-Y_{2}\left( \dot{v}_{1d}\right) \hat{\eta}% _{2}-e_{p1}-K_{4}e_{v1}\right], \end{equation} | (38) |
where $K_{4}={\rm diag}\left( \lambda _{2,1},\lambda _{2,2}\right) \in {\bf R}% ^{2\times 2}$ is a diagonal matrix of positive control gains, $\hat{\eta}_{2}$ is the online estimation of unknown parameter $\eta_{2}$. The adaptive updating law of unknown parameter can be designed as follows:
| \begin{equation} \dot{\hat{\eta}}_{2}=\gamma _{2}Y_{2}^{\rm T}\left( \dot{v}_{1d}\right) e_{v1}, \end{equation} | (39) |
where $\gamma _{2}\in {\bf R}$ is a positive,constant adaptation gain. Substituting (38) into (37),we can derive the closed-loop horizontal velocity tracking error dynamics as:
| \begin{equation} m\dot{e}_{v1}=Y_{2}\left( \dot{v}_{1d}\right) \tilde{\eta}% _{2}-e_{p1}-K_{4}e_{v1}-T_{M}e_{r}, \end{equation} | (40) |
where $\tilde{\eta}_{2}=\eta _{2}-\hat{\eta}_{2}\in {\bf R}$ denotes the unknown parameter estimation error.
Step 6. By differentiating (36) with respect to time and substituting the orientation dynamics into the resulting equation, the open-loop orientation error dynamics can be written as follows:
| \begin{equation} \dot{e}_{r}=\dot{r}_{d}-\Pi \omega _{1}. \end{equation} | (41) |
In this step,we take $\omega _{1d}$ as the desired roll-pitch angular velocity vector,and define the roll-pitch angular velocity tracking error as:
| \begin{equation} e_{\omega 1}=\omega _{1d}-\omega _{1}. \end{equation} | (42) |
| \begin{equation} \dot{e}_{r}=\dot{r}_{d}-\Pi \omega _{1d}+\Pi _{0}e_{\omega}, \end{equation} | (43) |
where $\Pi _{0}=\left[ \begin{array}{cc} \Pi & \mathbf{0}_{2\times 1}% \end{array}% \right] $. Based on the form of the open-loop dynamics of (43), the virtual control input $\omega _{1d}$ is designed as follows:
| \begin{equation} \omega _{1d}=\Pi ^{-1}\left( \dot{r}_{d}+\Lambda _{1}e_{r}-T_{M}e_{v1}\right), \end{equation} | (44) |
where $\Lambda _{1}={\rm diag}\left( \lambda _{3,1},\lambda _{3,2}\right) \in {\bf R}% ^{2\times 2}$ is a diagonal matrix of positive control gains. Substituting (44) into (43) produces the closed-loop dynamics for $e_{r}\left( t\right) $ as shown below
| \begin{equation} \dot{e}_{r}=-\Lambda _{1}e_{r}+T_{M}e_{v1}+\Pi _{0}e_{w}. \end{equation} | (45) |
Step 7. Let the angular velocity tracking error be defined as follows:
| \begin{equation} e_{\omega }=\omega _{d}-\omega. \end{equation} | (46) |
Then the angular velocity tracking error dynamics will have the following form
| \begin{equation} J\dot{e}_{\omega }=J\dot{\omega}_{d}+S\left( \omega ^{B}\right) J\omega ^{B}-A\left( T_{M}\right) v_{c}-B\left( T_{M}\right). \end{equation} | (47) |
On account of the inertia matrix uncertainty in the error dynamics,in this step we adopt adaptive control to estimate unknown parameters on line. In the same way,we make some changes to the corresponding terms of the right side of (47) as follows:
| \begin{equation} J\dot{\omega}_{d}+S\left( \omega ^{B}\right) J\omega ^{B}=Y_{3}\left( \dot{\omega}_{d},\omega ^{B}\right) \Delta, \end{equation} | (48) |
| \begin{equation} A\left( T_{M}\right) v_{c}+B\left( T_{M}\right) =\tau, \end{equation} | (49) |
where $\Delta =\left[ \begin{array}{ccc} \delta _{1} & \delta _{2} & \delta _{3}% \end{array}% \right] ^{\rm T}\in {\bf R}^{3}$ represents the unknown moment coefficients of the inertia matrix of the helicopter. According to (48),we know that the unknown parameters satisfy the condition of LP. Thus,the open-loop angular velocity error dynamics can be revised in the following advantageous form
| \begin{equation} J\dot{e}_{\omega }=Y_{3}\left( \dot{\omega}_{d},\omega ^{B}\right) \Delta -\tau. \end{equation} | (50) |
Here we design the general control input $\tau$ as follows:
| \begin{equation} \tau =Y_{3}\left( \dot{\omega}_{d},\omega ^{B}\right) \hat{\Delta}+\Lambda _{2}e_{\omega }+e_{\psi }\epsilon \left( \phi ,\theta \right) ^{\rm T}+\Pi _{0}^{\rm T}e_{r}, \end{equation} | (51) |
where $\Lambda _{2}={\rm diag}\left( \lambda _{4,1},\lambda _{4,2},\lambda _{4,3}\right) \in {\bf R}% ^{3\times 3}$ is a diagonal matrix of positive control gains, $\hat{\Delta}$ is the online estimation of unknown parameters $\Delta $. Therefore,the choice of control input $v_{c}$ will be
| \begin{equation} v_{c}=A^{-1}\left( T_{M}\right) \left[-B\left( T_{M}\right) +\tau \right]. \end{equation} | (52) |
The adaptive updating law of unknown parameters can be designed as follows:
| \begin{equation} \dot{\hat{\Delta}}=\Gamma _{3}Y_{3}^{\rm T}\left( \dot{\omega}_{d},\omega ^{B}\right) e_{\omega }, \end{equation} | (53) |
where $\Gamma _{3}={\rm diag}\left( \gamma _{3,1},\gamma _{3,2},\gamma _{3,3}\right) \in {\bf R}^{3\times 3}$ is a diagonal matrix of positive adaptation gains. Substituting (51) into (50), we can derive the closed-loop angular velocity tracking error dynamics as
| \begin{equation} J\dot{e}_{\omega }=Y_{3}\left( \dot{\omega}_{d},\omega ^{B}\right) \tilde{% \Delta}-\Lambda _{2}e_{\omega }-e_{\psi }\epsilon \left( \phi ,\theta \right) ^{\rm T}-\Pi _{0}^{\rm T}e_{r}, \end{equation} | (54) |
where $\tilde{\Delta}=\Delta -\hat{\Delta}\in {\bf R}^{3}$ denotes the unknown parameters estimation error vector.
Similarly,we define a Lyapunov function candidate for this subsystem,denoted by $V_{3}(t)\in {\bf R}$,as follows:
| \begin{align} V_{3} &=\frac{1}{2}e_{p1}^{\rm T}e_{p1}+\frac{1}{2}me_{v1}^{\rm T}e_{v1}+\frac{1}{2}% e_{r}^{\rm T}e_{r}+\frac{1}{2}e_{\omega }^{\rm T}Je_{\omega } +\nonumber \\ &\frac{1}{2}\gamma _{2}^{-1}\tilde{\eta}_{2}^{2}+\frac{% 1}{2}\tilde{\Delta}^{\rm T}\Gamma _{3}^{-1}\tilde{\Delta}. \label{Lyapunovfunction3} \end{align} | (55) |
By taking the time derivative of (55) and making the appropriate substitutions from (32),(39),(40),(45),(53) and (54),we derive the following expression:
| \begin{align} \dot{V}_{3} &=-e_{p1}^{\rm T}K_{3}e_{p1}-e_{v1}^{\rm T}K_{4}e_{v1}-e_{r}^{\rm T}\Lambda _{1}e_{r}-e_{\omega }^{\rm T}\Lambda _{2}e_{\omega } -\nonumber \\ &e_{\psi }e_{\omega }^{\rm T}\epsilon \left( \phi ,\theta \right) ^{\rm T}. \end{align} | (56) |
Theorem 1. The control input $T_{M}$ of (16),$v_{c}$ of (52),the adaptive updating law $\hat{\eta}_{1}$ of (17),$\hat{\eta}_{2}$ of (39) and $\hat{\Delta}$ of (53) can ensure the global asymptotic convergence of the position and yaw tracking errors as illustrated by
| \begin{equation} \underset{t\rightarrow \infty }{\lim }(e_{p}\left( t\right) ,e_{\psi }\left( t\right)) =0. \end{equation} | (57) |
Proof. To prove the above result,we define a composite Lyapunov function candidate $V(t)\in {\bf R}$ as follows:
| \begin{equation} V=V_{1}+V_{2}+V_{3}. \end{equation} | (58) |
Taking the time derivative of (58),we can get the following inequality
| \begin{align} \dot{V} &\leq -k_{1}\left\Vert e_{pz}\right\Vert ^{2}-k_{2}\left\Vert e_{vz}\right\Vert ^{2}-\lambda _{\psi }\left\Vert e_{\psi }\right\Vert ^{2} -\nonumber \\ &\lambda _{\min}\left\{ K_{3}\right\} \left\Vert e_{p1}\right\Vert ^{2}-\lambda _{\min}\left\{ K_{4}\right\} \left\Vert e_{v1}\right\Vert ^{2}- \nonumber \\ &\lambda _{\min}\left\{ \Lambda _{1}\right\} \left\Vert e_{r}\right\Vert ^{2}-\lambda _{\min}\left\{ \Lambda _{2}\right\} \left\Vert e_{\omega }\right\Vert ^{2}, \end{align} | (59) |
where $\lambda _{\min}\left\{ \cdot \right\} $ denotes the minimum eigenvalue of a matrix.
According to the form of (59),we know that $V\left( t\right) $ is either decreasing or constant. Since $V\left( t\right) $ of (58) is a non-negative function,we can conclude that $V\left( t\right) \in \mathcal{L}_{\infty }$. According to (58),we know that $e_{pz},e_{vz},e_{\psi },e_{p1},e_{v1},e_{r},e_{\omega },\tilde{\eta}_{1},% \tilde{\eta}_{2},\tilde{\Delta}\in \mathcal{L}_{\infty }$. From (11),(17),(18),(25),(32),(39),(40),(45),(53),(54), we know that $\dot{e}_{pz},\dot{e}_{vz},\dot{e}_{\psi },\dot{e}_{p1},\dot{e}_{v1},\dot{e}% _{r},\dot{e}_{\omega },\dot{\hat{\eta}}_{1},\dot{\hat{\eta}}_{2},\dot{\hat{\Delta}}% \in \mathcal{L}_{\infty }$. Thus,we have illustrated that all signals in the adaptive backstepping controller and in the system remain bounded during the closed-loop operation. Furthermore,the form of (59) allows us to show that $e_{pz},e_{vz},e_{\psi },e_{p1},e_{v1},e_{r},e_{\omega }\in \mathcal{L}_{2}$. With the above information,we can now invoke Barbalat$'$s lemma[16] to achieve the result of (57). Form (16) and (52),we know that $T_{M},v_{c}\in \mathcal{L}_{\infty }$.
Ⅴ. SIMULATION RESULTSThis section presents the simulation results of the control algorithm. The helicopter model parameters are taken form [7]. The desired position and yaw reference trajectories are
| \begin{equation} \begin{array}{ll} x_{r}\left( t\right) =10\left( 1-{\rm e}^{-0.25t}\right),& y_{r}\left( t\right) =10\left( 1-{\rm e}^{-0.25t}\right),\\ z_{r}\left( t\right) =5\left( 1-{\rm e}^{-0.25t}\right),& \psi _{r}\left( t\right) =0. \end{array} \label{referencetrajectory} \end{equation} | (60) |
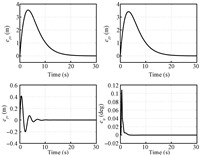
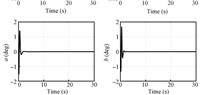
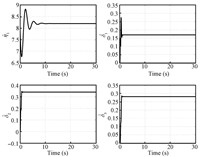
The initial states of the helicopter are set to 0. The initial values for parameter estimation are set as $\hat{\eta}_{1}\left( 0\right)=\hat{\eta}_{2}\left( 0\right)=8$,$\hat{\delta}_{1}\left( 0\right)=\hat{\delta}_{2}\left( 0\right)=\hat{\delta}_{3}\left( 0\right)=0$. The control gains are chosen as $k_{1}=0.9$, $k_{2}=1.5$,$K_{3}={\rm diag}\{0.4,0.4\} $,$K_{4}={\rm diag}\{ 1,1\}$,$\Lambda _{1}={\rm diag}\{ 1,2\} $,$\Lambda _{2}={\rm diag}\{ 1,1,1\} $,$\lambda _{\psi }=1$. The adaptation gains are selected as $\gamma _{1}=0.32$,$\gamma _{2}=1$,$\Gamma _{3}={\rm diag}\{7,7,1\,700\} $. The position and yaw tracking errors are illustrated in Fig.2. The four control inputs are provided in Fig.3. The parameter estimations can be seen in Fig.4. It can be seen that the satisfactory tracking performance is achieved in the presence of parametric uncertainties.
|
Download:
|
| Fig.2. Position and yaw tracking errors. | |
|
Download:
|
| Fig.3. Control inputs of $T_{M}$, $T_{T}$, $a$ and $b$. | |
|
Download:
|
| Fig.4. Parameter estimations of mass and moment coefficients. | |
This paper has presented an adaptive backstepping control design for the unmanned helicopter associated with parametric uncertainties of helicopter$'$s mass and moment coefficients. In order to facilitate the control design,we divide the helicopter$'$s dynamic model into three subsystems,which are altitude subsystem,yaw subsystem and horizontal subsystem. Since there is no strong coupling between these subsystems,the controller for each subsystem can be developed separately. The proposed controller combines the backstepping method with online parameter update laws to achieve the control objective. The GAS of the closed-loop system is rigorously proved by the Lyapunov based stability analysis.
In this paper,we have not considered the parametric uncertainties associated with the input matrix of $A\left( T_{M}\right) $ and $B\left( T_{M}\right) $. In order to ensure the robust performance of the unmanned helicopter system,we should combine the adaptive control method with robust control method to achieve superior control performance in the future research.
| [1] | Cai G W, Chen B M, Lee T H. Unmanned Rotorcraft Systems. London:Springer-Verlag, 2011. 1-5 |
| [2] | Shim D H, Kim H J, Sastry S. Control system design for rotorcraftbased unmanned aerial vehicles using time-domain system identification. In:Proceedings of the 2000 IEEE International Conference on Control Applications. Anchorage, USA:IEEE, 2000.808-813 |
| [3] | Gavrilets V. Autonomous Aerobatic Maneuvering of Miniature Helicopters[Ph. D.dissertation] Massachusetts Institute of Technology, Boston, USA, 2003. |
| [4] | La Civita M, Papageorigious G, Messner W C, Kanade T. Design and flight testing of a gain-scheduled H∞ loop shaping controller for wideenvelope flight of a robotic helicopter. In:Proceedings of the 2003 American Control Conference. Denver, USA:IEEE, 2003.4195-4200 |
| [5] | Takahashi M D, Schulein G, Whalley M. Flight control law design and development for an autonomous rotorcraft. In:Proceedings of the 64th American Helicopter Society International Annual Forum. Montreal, Canada:AHS International, Inc., 2008. 1652-1671 |
| [6] | Koo T J, Sastry S. Output tracking control design of a helicopter model based on approximate linearization. In:Proceedings of the 37th IEEE Conference on Decision & Control. Tampa, USA:IEEE, 1998.3635-3640 |
| [7] | Raptis I A, Valavanis K P, Moreno W A. A novel nonlinear backstepping controller design for helicopters using the rotation matrix. IEEE Transactions on Control System Technology, 2011, 19(2):465-473 |
| [8] | Ahmed B, Pota H R. Flight control of a rotary wing UAV using adaptive backstepping. In:Proceedings of the 2009 IEEE International Conference on Control and Automation. Christchurch, New Zealand:IEEE, 2009.1780-1785 |
| [9] | Isidori A, Marconi L, Serrani A. Robust nonlinear motion control of a helicopter. IEEE Transactions on Automatic Control, 2003, 48(3):413-426 |
| [10] | Marconi L, Naldi R. Robust full degree-of-freedom tracking control of a helicopter. Automatica, 2007, 43(11):1909-1920 |
| [11] | Shin J H, Kim H J, Kim Y D, Dixon W E. Autonomous flight of the rotorcraft-based UAV using RISE feedback and NN feedforward terms. IEEE Transactions on Control System Technology, 2012, 20(5):1392-1399 |
| [12] | Sugeno M, Hirano I, Nakamura S, Korsu S. Development of an intelligent unmanned helicopter. In:Proceedings of the 4th IEEE International Conference on Fuzzy Systems. Yokohama, Japan:IEEE, 1995.33-34 |
| [13] | Johnson E N, Kannan S K. Adaptive trajectory control for autonomous helicopters. Journal of Guidance, Control, and Dynamics, 2005, 28(3):524-538 |
| [14] | Lee T Y. Geometric tracking control of the attitude dynamics of a rigid body on SO(3). In:Proceedings of the 2011 American Control Conference. San Francisco, USA:IEEE, 2011.1200-1205 |
| [15] | Kanellakopoulos I, Kokotovic P V, Morse A S. Systematic design of adaptive controllers for feedback lineatization systems. IEEE Transactions on Automatic Control, 1991, 36(11):1241-1253 |
| [16] | Slotine J E, Li W P. Applied Nonlinear Control. Englewood Cliffs:Prentice Hall, 1991. 122-126 |
 2015, Vol.2
2015, Vol.2 


