COMPARED to unmanned combat aerial vehicles (UCAVs) that perform solo missions,greater efficiency and operational capability can be realized from teams of UCAVs operating in a coordinated fashion[1, 2, 3, 4, 5]. Designing UCAVs with intelligent and coordinated action capabilities to achieve an overall objective is a major part of multiple UCAVs control in a complicated and uncertain environment[6, 7, 8, 9, 10]. Actually,a military air operation involving multiple UCAVs is a complex dynamic system with many interacting decision-making units which have even conflicting objectives. Modeling and control of such a system is an extremely challenging task,whose purpose is to seek a feasible and optimal scheme to assign the limited combat resource to specific units of the adversary while taking into account the adversary$'$s possible defense strategies[8, 11]. The difficulty lies not only in that it is often very difficult to mathematically describe the underlying processes and objectives of the decision maker but also in that the fitness of one decision maker depends on both its own control input and the opponent$'$s strategies as well.
Dynamic game theory has received increasingly intensive attention as a promising technique for formulating action strategies for agents in such a complex situation,which involves competition against an adversary. The priority of game theory in solving control and decision-making problems with an adversary opponent has been shown in many studies[12, 13, 14, 15]. A game theory approach was proposed for target tracking problems in sensor networks in [14],where the target is assumed to be an intelligent agent who is able to maximize filtering errors by escaping behavior. The pursuit-evasion game formulations were employed in [16] for the development of improved interceptor guidance laws. Cooperative game theory was used to ensure team cooperation by Semsar-Kazerooni et al.[13],where a team of agents aimed to accomplish consensus over a common value for their output.
Although finding the Nash equilibrium in a two-player game may be easy since the zero-sum version can be solved in polynomial time by linear programming,this problem has been proved to be indeed PPAD-complete[17, 18]. So the problem of computing Nash equilibria in games is computationally extremely difficult,if not impossible. Based on the analogy of the swarm of birds and the school of fish,Kennedy and Eberhart developed a powerful optimization method,particle swarm optimization (PSO)[19, 20],addressing the social interaction,rather than purely individual cognitive abilities. As one of the most representative method aiming at producing computational intelligence by simulating the collective behavior in nature,PSO has been seen as an attractive optimization tool for the advantages of simple implementation procedure,good performance and fast convergence speed. However,it has been shown that this method is easily trapped into local optima when coping with complicated problems,and various tweaks and adjustments have been made to the basic algorithm over the past decade[20, 21, 22]. To overcome the aforementioned problems,a hybrid predator-prey PSO (PP-PSO) was firstly proposed in [21] by introducing the predator-prey mechanism in the biological world to the optimization process.
Recently,bio-inspired computation in UCAVs have attracted much attention[23, 24, 25]. However,the game theory and solutions to the problem of task assignment have been studied independently. The main contribution of this paper is the development of a game theoretic approach to dynamic UCAV air combat in a military operation based on the PP-PSO algorithm. The dynamic task assignment problem is handled from a game theoretic perspective,where the assignment scheme is obtained by solving the mixed Nash equilibrium using PP-PSO at each decision step.
The remainder of the paper is organized as follows: Section II describes the formulation of the problem,including the attrition model of a military air operation and its game theoretic representation. Subsequently,we propose a predator-prey PSO for the mixed Nash equilibrium computing of two-player,non-cooperative game in Section III. An example of an adversary scenario of UCAV combat involving two opposing sides is presented in Section IV to illustrate the effectiveness and adaption of the proposed methodology. Concluding remarks are offered in the last section.
Ⅱ. A DYNAMIC GAME THEORETIC FORMULATION FOR UCAV AIR COMBAT A. Dynamic Model of UCAV Air CombatThere are two combat sides in the UCAV air combat model. Specifically,the attacking side is labeled as $Red$ and the defending force as $Blue$. Each side consists of different combat units,which are made up of different numbers of combat platforms armed with weapons. Each unit is fully described by its location, number of platforms and the average number of weapons per platform. Thus,the state of each unit at time k is defined as $\xi _{i}^{X}\left( k \right)=\left[x_{i}^{X}\left( k \right),y_{i}^{X}\left( k \right),p_{i}^{X}\left( k \right)w_{i}^{X}\left( k \right) \right]$,where $X$ denotes the $Red$ force or $Blue$ force,$\left[x_{i}^{X}\left( k \right),y_{i}^{X}\left( k \right) \right]$ represents the unit location,$p_{i}^{X}\left( k \right)$ corresponds to the number of platforms of the $i\text{th}$ unit at time $k$,and $w_{i}^{X}\left( k \right)$ to the number of weapons on each platform in the $i\text{th}$ unit of $X$. The number of platforms for the moving units changes according to the following attrition equations
| \begin{equation} p_{i}^{X}\left( k+1 \right)=p_{i}^{X}\left( k \right)A_{i}^{k}\left( k \right). \end{equation} | (1) |
The term in (1) represents the percentage of platforms in the $i\text{th}$ unit of $X$ force,which survive the transition from time $k$ to $k+1$. For each unit in force $X$,this percentage is dependent on the identities of the attacking and the attacked units determined by the choice of target control,and is expressed as
| \begin{equation} A_{i}^{X}\left( k \right)=1-\sum\limits_{j=1}^{{{N}_{d}}}{Q_{ij}^{XY}\left( k \right)P_{ij}^{XY}\left( k \right)}. \end{equation} | (2) |
It is assumed in (2) that ${{N}_{d}}$ units of $Y$ fire at the $i\text{th}$ unit of $X$. The engagement factor $Q_{ij}^{XY}\left( k \right)$ of the $j\text{th}$ unit of $Y$ attacking the $i\text{th}$ unit of $X$ at time $k$ is computed from
| \begin{equation} Q_{ij}^{XY}=\beta _{ij}^{XY}\left[1-\exp\left( \frac{-p_{j}^{Y}(k)}{p_{i}^{X}(k) }\right)\right], \end{equation} | (3) |
where $\beta _{ij}^{XY}$ represents the probability that the $j\text{th}$ unit of $Y$ acquires the $i\text{th}$ unit of $X$ as a target,and is calculated by
| \begin{equation} \beta _{ij}^{XY}=\left\{ \begin{matrix} 1,& \text{if}\ p_{j}^{Y}-p_{i}^{X}\ge 0,\\ \exp \left( p_{j}^{Y}-p_{i}^{X} \right),& \text{if}\ p_{j}^{Y}-p_{i}^{X}<0. \\ \end{matrix} \right. \end{equation} | (4) |
The attrition factor $P_{ij}^{XY}\left( k \right)$ in (2) represents the probability of the platforms in the $i\text{th}$ unit of $X$ being destroyed by the salvo of $s_{j}^{Y}\left( k \right)$ fired from the $j\text{th}$ unit of $Y$ at time $k$,and is computed as follows
| \begin{equation} P_{ij}^{XY}\left( k \right)=\left[1-{{\left( 1-{{\beta }_{w}}PK_{ij}^{XY} \right)}^{S_{j}^{Y}\left( k \right)}} \right], \end{equation} | (5) |
where the term $0\le {{\beta }_{w}}\le 1$ represents the weather impact which reduces the kill probability according to the weather condition,i.e.,1 corresponds to ideal weather condition while 0 corresponds to the worst weather condition. $PK_{ij}^{XY}$ is the probability of $i\text{th}$ unit of $X$ being completely destroyed by the $j\text{th}$ unit of $Y$ under ideal weather and terrain conditions.
In the equation mentioned above $s_{i}^{Y}$ is the average effective kill factor when the $j\text{th}$ unit of $X$ attacks the $i\text{th}$ unit of $Y$ with salvo $c_{i}^{Y}\left( k \right)$,and is calculated from
| \begin{equation} s_{j}^{Y}=\frac{c_{j}^{Y}\left( k \right)p_{j}^{Y}\left( k \right)}{p_{i}^{X}\left( k \right)}{{\left( \frac{p_{j}^{Y}\left( k \right)}{p_{i}^{X}\left( k \right)} \right)}^{c -1}}, \end{equation} | (6) |
where $c_{i}^{Y}$ is the salvo size of $j\text{th}$ combat unit of $Y$ and $c$ is a constant referred to as Wes coefficient.
The control vector for each unit for both sides is chosen as
| \begin{equation} u_{i}^{X}\left( k \right)=\left[\begin{matrix} V_{{{x}_{i}}}^{X}\left( k \right) & V_{{{y}_{i}}}^{X} \left( k \right) & c_{{{x}_{i}}}^{X}\left( k \right) & d_{{{x}_{i}}}^{X}\left( k \right) \\ \end{matrix} \right], \end{equation} | (7) |
where $V_{{{x}_{i}}}^{X}\left( k \right)$ and $V_{{{y}_{i}}}^{X}\left( k \right)$ are respectively the relocating control corresponding to the $x$-coordinate and $y$-coordinate,$d_{{{x}_{i}}}^{X}\left( k \right)$ is the number of units that fire at $i\text{th}$ unit of $X$,and $c_{{{x}_{i}}}^{X}\left( k \right)$ is the salvo size control variable that decides how many weapons should fire. The number of weapons is updated according to
| \begin{equation} w_{i}^{X}\left( k+1 \right)=w_{i}^{X}\left( k \right)-c_{i}^{X}\left( k \right). \end{equation} | (8) |
The state equations of each unit engaged in an air combat are defined as
| \begin{equation} \left\{\begin{array}{*{20}lll} x_{i}^{X}\left( k+1 \right)=x_{i}^{X}\left( k \right)+V_{{{x}_{i}}}^{X}\left( k \right),\\ y_{i}^{X}\left( k+1 \right)=y_{i}^{X}\left( k \right)+V_{{{y}_{i}}}^{X}\left( k \right) ,\\ p_{i}^{X}\left( k+1 \right)=p_{i}^{X}\left( k \right)A_{i}^{k}\left( k \right) ,\\ w_{i}^{X}\left( k+1 \right)=w_{i}^{X}\left( k \right)+c_{i}^{X}\left( k \right) . \\ \end{array}\right. \end{equation} | (9) |
The problem of dynamic task assignment in the air combat is modeled from a game theoretic perspective in this paper. Suppose $Red$ consists of ${NR}$ units (UCAVs) and it fires $CR$ missiles during each attack or defense. There are ${NB}$ units in the $Blue$ force,whose salvo size is also a constant $CB$. At each decision making step $k$,both sides decide on which units of its own side should be chosen to attack and which units of the opponent should be chosen as targets,with the purpose of maximizing its own objective function. Each combination of attacking and attacked units is seen as a pure strategy in the game. For each side,the number of pure strategies is calculated as
| \begin{equation} {{N}_{RS}}=C_{NR}^{CR}\cdot C_{NB}^{CR}\cdot {CR}!, \end{equation} | (10) |
| \begin{equation} {{N}_{BS}}=C_{NR}^{CB}\cdot C_{NB}^{CB}\cdot {CB}!. \end{equation} | (11) |
The payoff matrix for both sides is an ${{N}_{RS}}\times
| $\begin{align} & M{{R}_{{{N}_{RS}}\times {{N}_{RS}}}}= \\ & \left[\begin{matrix} {{J}_{1,1}}^{R}(k) & {{J}_{1,2}}^{R}(k) & \cdots & {{J}_{1,{{N}_{BS}}}}^{R}(k) \\ {{J}_{2,1}}^{R}(k) & {{J}_{2,2}}^{R}(k) & \cdots & {{J}_{2,{{N}_{BS}}}}^{R}(k) \\ \vdots & \vdots & \ddots & \vdots \\ {{J}_{{{N}_{RS}},1}}^{R}(k) & {{J}_{{{N}_{RS}},2}}^{R}(k) & \cdots & {{J}_{{{N}_{RS}},{{N}_{BS}}}}^{R}(k) \\ \end{matrix} \right],\\ \end{align}$ | (12) |
| \begin{align} &{{MB}_{{{N}_{RS}}\times {{N}_{BS}}}}= \nonumber\\ &\quad \left[\begin{matrix} {{J}_{1,1}}^{B}(k) & {{J}_{1,2}}^{B}(k) & \cdots & {{J}_{1,{{N}_{BS}}}}^{B}(k) \\ {{J}_{2,1}}^{B}(k) & {{J}_{2,2}}^{B}(k) & \cdots & {{J}_{2,{{N}_{BS}}}}^{B}(k) \\ \vdots & \vdots & \ddots & \vdots \\ {{J}_{{{N}_{RS}},1}}^{B}(k) & {{J}_{{{N}_{RS}},2}}^{B}(k) & \cdots & {{J}_{{{N}_{RS}},{{N}_{BS}}}}^{B}(k) \\ \end{matrix} \right]. \end{align} | (13) |
Each entry $J_{i,j}^{R}\left( k \right)$ in $MR$ corresponds to the payoff of $Red$ when it takes the $i\text{th}$ pure strategy against the $j\text{th}$ pure strategy of $Blue$. For the attacking force of $Red$,the objective function $J_{i,j}^{R}\left( k \right)$ is calculated as
| \begin{equation} J_{{}}^{R}(k)=\sum\limits_{i=1}^{{{N}_{R}}}{{{\varepsilon }_{i}}}\frac{{{p}_{i}}^{R}(k)}{{{p}_{i}}^{R}(0)}-\sum\limits_{i=1}^{{{N}_{B}}}{{{\tau }_{i}}}\frac{{{p}_{i}}^{B}(k)}{{{p}_{i}}^{B}(0)}, \end{equation} | (14) |
where $\varepsilon $ and $\tau $ are weight coefficients. The objection function for the defense of $Blue$ is calculated,by the same token,as
| \begin{equation} J_{{}}^{B}(k)=-\sum\limits_{i=1}^{{{N}_{R}}}{a{{'}_{i}}}\frac{{{p}_{i}}^ {R}(k)}{{{p}_{i}}^{R}(0)}+\sum\limits_{i=1}^{{{N}_{B}}}{b{{'}_{i}}}\frac{{{p}_{i}} ^{B}(k)}{{{p}_{i}}^{B}(0)}. \end{equation} | (15) |
From a game theoretic point of view,the cooperative UCAV task assignment problem is for the tagged side,$Red$,to maximize its own payoff at each decision step,by calculating a mixed Nash equilibrium for the ${{N}_{RS}}\times {{N}_{BS}}$ matrix game.
Ⅲ. PREDATOR-PREY PSO FOR THE MIXED NASH SOLUTION A. Predator-prey PSOIn the $gbest$-model of PSO,each particle has information of its current position and velocity in the solution space[21]. And it has the best solution found so far of itself as $pbest$ and the best solution of a whole swarm as $gbest$. The $gbest$-model can be expressed as
| \begin{align} {{v}_{ij}}(k+1)&=\omega {{v}_{ij}}(k)+{{c}_{1}}{{r}_{1}}[{{p}_{i}}(k)-{{x}_{ij}}(k)]+ \nonumber\\ &{{c}_{2}}{{r}_{2}}[{{g}_{i}}(k)-{{x}_{ij}}(k)], \end{align} | (16) |
| \begin{equation} {{x}_{ij}}(k+1)={{x}_{ij}}(k)+{{v}_{ij}}(k+1), \end{equation} | (17) |
where ${{v}_{ij}}(k)$ and ${{x}_{ij}}(k)$ respectively denote the velocity and position of the $i\text{th}$ particle in the $j\text{th}$ dimension at step $k$,and ${{c}_{1}}$ and ${{c}_{2}}$ are weight coefficients,${{r}_{1}}$ and ${{r}_{2}}$ are random numbers between 0 and 1 to reflect the stochastic algorithm nature. The personal best position ${{p}_{i}}$ corresponds to the position in the search space where particle $i$ has the minimum fitness value. The global best position denoted by ${{g}_{i}}$ represents the position yielding the best fitness value among all the particles.
Unfortunately,the basic PSO algorithm is easy to fall into local optima. In this condition,the concept of predator-prey behavior is introduced into the basic PSO to improve the optima finding performance[26, 27, 28]. This adjustment takes a cue from the behavior of schools of sardines and pods of killer whales. In this model,particles are divided into two categories,predator and prey. Predators show the behavior of chasing the center of preys$'$ swarm; they look like chasing preys. And preys escape from predators in the multidimensional solution space. After taking a tradeoff between predation risk and their energy, escaping particles would take different escaping behaviors. The velocities of the predator and the prey in the PP-PSO can be defined by
| \begin{align} &{{v}_{dij}}(k+1)={{\omega }_{d}}{{v}_{dij}}(k)+{{c}_{1}}{{r}_{1}}[{{p}_{dij}}(k)-{{x}_{dij}}(k)]+ \nonumber\\ &\qquad {{c}_{2}}{{r}_{2}}[{{g}_{dj}}(k)-{{x}_{dij}}(k)]+{{c}_{3}}{{r}_{3}} [{{g}_{j}}(k)-{{x}_{dij}}(k)],\\ &{{v}_{rij}}(k+1)={{\omega }_{r}}{{v}_{rij}}(k)+{{c}_{4}}{{r}_{4}}[{{p}_{rij}}(k)-{{x}_{rij}}(k)]+ \nonumber\\ &\qquad{{c}_{5}}{{r}_{5}}[{{g}_{rj}}(k)-{{x}_{rij}}(k)]+{{c}_{6}}{{r}_{6}}[{{g}_{j}}(k)-{{x}_{rij}}(k)]- \nonumber\\ &\qquad Pasign[{{x}_{dIj}}(k)-{{x}_{rij}}(k)] \exp[-b|{{x}_{dIj}}(k)-{{x}_{rij}}(k)|], \end{align} | (18) |
where $d$ and $r$ denote the predator and prey,respectively, ${{p}_{di}}$ is the best position of predators,${{p}_{ri}}$ is the best position of preys,$g$ is the best position which all the particles have ever found. And ${{\omega }_{d}}$ and ${{\omega }_{r}}$ are defined as
| \begin{equation} {{\omega }_{d}}=0.2\exp \left( -10\frac{iteration}{iteratio{{n}_{\max }}} \right)+0.4, \end{equation} | (20) |
| \begin{equation} {{\omega }_{r}}={{\omega }_{\max }}-\frac{{{\omega }_{\max }}-{{\omega }_{\min }}}{iteratio{{n}_{\max }}}iteration, \end{equation} | (21) |
where ${{\omega }_{d}}$ and ${{\omega }_{r}}$ are the inertia weights of predators and preys,which regulate the trade-off between the global (wide-ranging) and local (nearby) exploration abilities of the swarm and are considered critical for the convergence behavior of PSO. $iteratio{{n}_{\max }}$ represents the maximum number of iterations and ${{\omega }_{\max }}$ and ${{\omega }_{\min }}$ denote the maximum and minimum value of ${{\omega }_{r}}$,respectively. And the definition of $I$ is given by the following expression
| \begin{equation} I=\{k|\underset{k}{\mathop{\min }}\,(|{{x}_{dk}}-{{x}_{ri}}|)\}. \end{equation} | (22) |
Then $I$ denotes the number of the $i\text{th}$ prey's nearest predator. In (18),$P$ is used to decide if the prey escapes or not ($P=0$ or $P=1$),and $a$ and $b$ are the parameters that determines the difficulty of the preys escaping from the predators. The closer the prey and the predator,the harder the prey escapes from the predator. Moreover,$a$ and $b$ are shown as
| \begin{equation} a={{x}_{span}},b=\frac{100}{{{x}_{span}}}, \end{equation} | (23) |
where ${{x}_{span}}$ is the span of the variable.
B. Nash EquilibriumAs a competitive (non-cooperative) strategy of multi-objective multi-criterion system first proposed by Nash[29],Nash equilibrium is basically a local optimum: a strategy profile (${{s}_{1}},{{s}_{2}},\cdots ,{{s}_{n}}$) such that no player can benefit from switching to a different strategy if nobody else switches,$\forall i,\forall {{s}'_{i}}\in {{S}_{j}}$
| \begin{align} {{U}_{{{P}_{j}}}}({{s}_{1}},\cdots,&{{s}_{i-1}},{{s}_{i}},{{s}_{i+1}},\cdots,{{s}_{n}}) \ge\nonumber\\ & {{U}_{{{P}_{j}}}}({{s}_{1}},\cdots,{{s}_{i-1}},{{s}^{'}_{i}},{{s}_{i+1}},\cdots,{{s}_{n}}), \end{align} | (24) |
where ${{U}_{{{P}_{j}}}}$ denotes the expected payment of person $j$,${{s}_{j}}$ and ${{S}_{j}}$ respectively denote the $i\text{th}$ strategy of player $j$ and the set of strategies. Note that every dominant strategy equilibrium is a Nash equilibrium,but not vice versa. Every game has one Nash equilibrium at least. In this paper,the expected payment is substituted by the objective function which is used to calculate the payoff matrixes denoted by $M{{A}_{m\times n}}$ and $M{{B}_{m\times n}}$. We define the vector of mixed strategies for both sides as ${{X}_{i}}=\left( {{x}_{i1}},\cdots,{{x}_{im}},{{y}_{i1}},\cdots,{{y}_{in}} \right)$,such that ${{x}_{ik}}\ge 0$,${{y}_{ik}}\ge 0$, $\sum\nolimits_{k=1}^{m}{{{x}_{ik}}}=1$, $\sum\nolimits_{k=1}^{n}{{{y}_{ik}}}=1$,where $m={{N}_{RS}}$ and $n={{N}_{BS}}$. So,for each mixed strategy ${{X}_{i}}$,the Nash equilibrium solution $\left( {{X}^{*}},{{Y}^{*}} \right)$ must satisfy the given conditions
| \begin{equation} \left\{ \begin{array}{*{35}{l}} MA{{\left( {{Y}^{*}} \right)}^{\prime }}\ge MA{{\left( {{X}_{i}}\left( m+1:m+n \right) \right)}^{\prime }} \\ {{X}^{*}}MB\ge {{X}_{i}}\left( 1:m \right)MB \\ \end{array} \right. \end{equation} | (25) |
For utilizing the proposed algorithm to compute Nash equilibrium here,we give the fitness functions as
| \[\begin{align} & f[{{X}_{di}}^{t}]= \\ & \underset{1\le j\le m}{\mathop{\max }}\,\{MR(j,:)(X_{di,m+1:m+n}^{t}{)}'- \\ & X_{di,1:m}^{t}MR(X_{di,m+1:m+n}^{t}{)}'\}+ \\ & \underset{1\le j\le n}{\mathop{\max }}\,\{X_{di,1:m}^{t}MB(:,j)- \\ & X_{di,1:m}^{t}MB\cdot (X_{di,m+1:m+n}^{t}{)}'\},\\ \end{align}\] | (26) |
| \[\begin{align} & f[{{X}_{ri}}^{t}]= \\ & \underset{1\le j\le m}{\mathop{\max }}\,\{MR(j,:)(X_{ri,m+1:m+n}^{t}{)}'- \\ & X_{ri,1:m}^{t}MR(X_{ri,m+1:m+n}^{t}{)}'\}+ \\ & \underset{1\le j\le n}{\mathop{\max }}\,\{X_{ri,1:m}^{t}MB(j,:)- \\ & X_{ri,1:m}^{t}MB(X_{ri,m+1:m+n}^{t}{)}'\}. \\ \end{align}\] | (27) |
In the last two expressions,${{X}_{di,1:m}}(k)$ means the mixed strategies which are produced by the $i\text{th}$ predator for the $A$ force and the $B$ force,respectively. Similarly, ${{X}_{ri,1:m}}(k)$ and ${{X}_{ri,m+1:m+n}}(k)$ denote the mixed strategies which are produced by the $i\text{th}$ prey for the $A$ and $B$ forces. Note that the proposed variables must satisfy the following conditions:
| \begin{equation} {{X}_{di,j}}(k)\ge 0,{{X}_{ri,j}}(k)\ge 0, \end{equation} | (28) |
| \begin{equation} \left\{ \begin{matrix} \sum\limits_{j=1}^{m}{{{X}_{di,j}}}=1,\sum\limits_{j=m+1}^{m+n}{{{X}_{di,j}}}=1,\\ \sum\limits_{j=1}^{m}{{{X}_{ri,j}}}=1,\sum\limits_{j=m+1}^{m+n}{{{X}_{ri,j}}}=1. \\ \end{matrix} \right. \end{equation} | (29) |
Importantly,the mixed Nash equilibrium corresponds to the minimum of the fitness function and the optimal or the sub-optimal solution will be the closest to zero. The detailed procedure of PP-PSO for the mixed Nash equilibrium computing is demonstrated in Fig. 1.

|
Download:
|
| Fig.1. Procedure of Nash equilibrium computing based on the PP-PSO. | |
To validate the effectiveness of the proposed method,here we illustrated the Nash equilibrium computing both for zero-sum game and non-zero-sum game using two simple examples. For a fair comparison among these two method,they use the same maximum iteration number ${{N}_{\max }}=100$,the same population size $m=30$,and the same up and lower bounds for inertia weights ${{\omega }_{\max }}=0.9$,${{\omega }_{\min }}=0.2$. Besides,in our proposed PP-PSO,the numbers of predators and preys are set ${{m}_{d}}=10$,${{m}_{r}}=20$, respectively.
Example 1. Consider two-person,zero-sum game and non-zero-sum game illustrated by Tables I and II[30].
|
|
Table I PAY-OFF MATRIX OF $A$ AND $B$ IN A TWO PLAYER, ZERO-SUM GAME |
|
|
Table II PAY-OFF MATRIX OF $A$ AND $B$ IN A TWO PLAYER, NON-ZERO-SUM GAME |
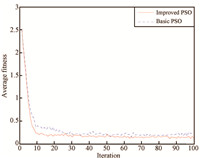
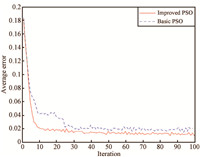
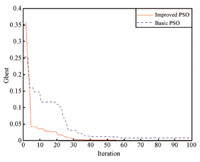
As we can see from the above two tables,the first column and the first row represents the strategies of player $A$ and $B$, respectively. For example,in the zero-sum game,each player has three strategies,which are specified by the number of rows and the number of columns. The payoffs are provided in the interior. The first number is the payoff received by the column player; the second is the payoff for the row player. To reduce statistical errors,each algorithm is tested 100 times independently for these two games. Evolution curves for the two-player,zero sum game are depicted in Figs.2$\sim$4. Besides,the simulation results are illustrated from the perspective of average fitness value, best fitness value ever found (Tables III and IV),the minimum error and times that the results satisfied that $error\le 0.01$, where $error$ is defined as the following expressions:
| \[\begin{align} & {{e}_{h}}(k)= \\ & \frac{\sum\limits_{i=1}^{{{m}_{d}}}{\left\| {{X}_{di,1:m+n}}(k)-E\_S \right\|}+\sum\limits_{i=1}^{{{m}_{r}}}{\left\| {{X}_{ri,1:m+n}}(k)-E\_S \right\|}}{{{m}_{d}}+{{m}_{r}}},\\ \end{align}\] | (30) |
| \[{{e}_{b}}(k)=\frac{\sum\limits_{i=1}^{{{m}_{b}}}{\left\| {{X}_{i,1:{{m}_{b}}}}(k)-E\_S \right\|}}{{{m}_{b}}},\text{ }\] | (31) |
|
Download:
|
| Fig.2. Comparison results of average fitness values for the two player, zero-sum game. | |
|
Download:
|
| Fig.3. Comparison results of average errors for the two player, zero-sum game. | |
|
Download:
|
| Fig.4. Comparison results of global best solutions for the two player, zero-sum game. | |
|
|
Table III COMPARISON RESULTS FOR THE TWO PLAYER, ZERO-SUM GAME |
|
|
Table IV COMPARISON RESULTS FOR THE TWO PLAYER, NON-ZERO-SUM GAME |
where ${{e}_{h}}(k)$ and ${{e}_{b}}(k)$ denote the error of the basic PSO and our proposed PP-PSO,$E\_S$ represents the mixed Nash equilibrium solution of the game that the players participate in. Note that for the zero-sum game shown in Table I,$E\_S=\left[ \frac{21}{52},\frac{12}{52},\frac{19}{52},\frac{2}{13},\frac{3}{13},\frac{8}{13} \right]$. And for the non-zero-sum game shown in Table II, $E\_S=\left[ \frac{1}{3},\frac{1}{3},\frac{1}{3},0,\frac{1}{3},\frac{1}{3},\frac{1}{3},0 \right]$.
It is reasonable to conclude from the simple example demonstrated above that the proposed PP-PSO outperforms the basic PSO in terms of solution accuracy,convergence speed,and reliability for Nash equilibrium computing. So it is appropriate to use this method to solve the problem of multiple UCAV air combat modeled by dynamic game theory in the following section.
Ⅳ. GAME THEORETIC APPROACH TO UCAV AIR COMBAT BASED ON PP-PSO A. Experimental SettingsTo validate the effectiveness of the dynamic game theoretic formulation for UCAV air combat,a computational example is performed based on Matlab 2009b using our proposed PP-PSO. Consider an adversary scenario involving two opposing forces here. The attacking force is labeled as $Red$ team,while the defending force is labeled as $Blue$ team. The mission of the $Blue$ force is transporting military supplements from its base to the battlefront while the task of the $Red$ force is attacking and destroying the aerotransports of the $Blue$ force at least 80\,$\%$ and then returning to their air base.
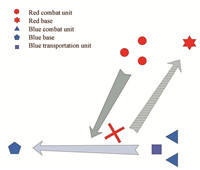
As shown in Fig. 5,the $Blue$ force consists of one transportation unit,which is represented by the solid square,and two combat units. They are on the way back to the base after accomplishing a military mission. The $Red$ force consists of three combat units and aims to destroy the $Blue$ transportation unit. The $Red$ force is also programmed to return the base after the mission. For simplification of the problem,each unit of both sides is assumed to consist of the same type of UCAVs,and each UCAV is equipped with a certain number of air-to-air missiles. Assume that the speed of $Red$ force is nearly 0.25 km/s while the speed of $Blue$ force is nearly 0.2 km/s,and the state variables will be updated every 2 minutes. So the positions of the $Red$ force and the $Blue$ force will change 30 km and 24 km,respectively at each step. The configuration parameters used in the simulation for the $Red$ force and the $Blue$ force are listed in Table V and Table VI, respectively.
|
Download:
|
| Fig.5. Scenario of cooperative UCAV task assignment. | |
|
|
Table V INITIAL CONFIGURATION OF $Red$ FORCE |
|
|
Table VI INITIAL CONFIGURATION OF $Blue$ FORCE |
In the simulation,the objective functions of the two forces are chosen as
| \begin{equation} J_{{}}^{R}(k)=\sum\limits_{i=1}^{3}{0.4}\frac{{{p}_{i}}^{R}(k)}{{{p}_{i}}^{R}(0)}- \frac{{{p}_{1}}^{B}(k)}{{{p}_{1}}^{B}(0)}-\sum\limits_{i=2}^{3}{0.3}\frac{{{p}_{i}}^{B}(k)}{{{p}_{i}}^{B}(0)}, \end{equation} | (32) |
| \begin{equation} J_{{}}^{B}(k)=-\sum\limits_{i=1}^{3}{0.6}\frac{{{p}_{i}}^{R}(k)}{{{p}_{i}}^{R}(0)}+ 0.5\frac{{{p}_{1}}^{B}(k)}{{{p}_{1}}^{B}(0)}+\sum\limits_{i=2}^{3}{0.5}\frac{{{p}_{i}}^{B}(k)}{{{p}_{i}}^{B}(0)}. \end{equation} | (33) |
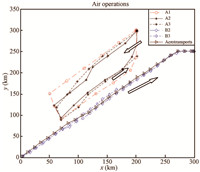
Fig. 6 presents the flying trajectories for both sides in the air military operations,which result from the proposed game theoretic formulation of task assignment in a dynamic combat environment and the PP-PSO based solution methodology. The $Red$ force starts from near its base and launches attacks to eliminate the $Blue$ transportation force,which is on the way returning to its base after a military mission. The task assignment scheme for both sides are calculated based on the proposed approach described above.
|
Download:
|
| Fig.6. Resulting trajectories of both sides from the proposed approach. | |
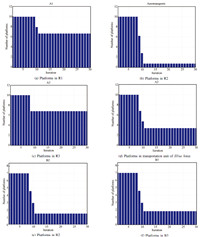
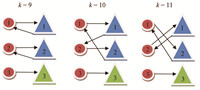
The detailed evolution and convergence behavior with time of platform numbers in combating units are shown in Fig. 7. The combating units of both sides start to fight at the 9th time step. After 3 time steps of engagement,this air military operation ends up at the 11th time step, with $Red$ defeating the $Blue$ force and the surviving forces of both sides returning to their own bases. At the end of the combat,the $Red$ force manages to inflict more than 90%of the platforms in $Blue'$s transportation unit, 78% of platforms in B2,and 70% of platforms in B3. Meanwhile, the $Red$ team pays a price for the victory. The first unit R1 and the third one R3 suffer a slight damage and 30% platforms are destroyed in the attack. However, the second unit R2 of the $Red$ force suffer a serious damage,with more than 60% of the platforms being destroyed in the engagement with the $Blue$ force. The result can be explained from Fig. 8,where snapshots of the dynamic task assignment results at Steps 9,10,and 11 are given. It illustrates that the engagement of both sides has a different pattern at each time step and proves the task assignment process to be a dynamic process with time. At the 9th and 10th time steps,the second unit R2 of the $Red$ force takes actions in accordance with the resulting mixed Nash equilibrium and chooses the first and second units of $Blue$ force as targets, respectively. However,the $Blue$ force insists on attacking R2 by the first unit B1, which is the most powerful unit of its 10 combat platforms. Consequently,R2 suffers the most serious damage in the three units of $Red$.
|
Download:
|
| Fig.7. Number of platforms. | |
|
Download:
|
| Fig.8. Snapshots of dynamic task assignment results. | |
It is important to note that both the attacking side and the defense side take advantage of the proposed approach to acquire the assignment scheme over the engagement duration. Therefore,the engagement outcome mainly depends on the initial configuration of each force. The $Red$ force has an advantage in performances and numbers of weapons,which implies the possible result of $Blue'$s defeat. The experimental results are coincident with the theoretical analysis and verify the effectiveness and feasibility of the proposed approach.
Ⅴ. CONCLUSIONSThis paper developed a game theoretic method for UCAV combat, which is based on the PP-PSO model. By considering both the adversary side and the attacking side as rational game participants,we represented the task allocation scheme as an optional policy set of both sides,and the cooperative task allocation results of both sides were achieved by solving the mixed Nash equilibrium using PP-PSO. An example of military operation involving an attacking side $Red$ and a defense side $Blue$ was presented to verify the effectiveness and adaptive ability of the proposed method. Simulation results show that the combination of game theoretic representation of the task assignment and the application of PP-PSO for the mixed Nash solutions can effectively solve the UCAV dynamic task assignment problem involving an adversary opponent.
| [1] | Richards A, Bellingham J, Tillerson M, How J. Coordination and control of multiple UAVs. In:Proceedings of the 2002 AIAA Guidance, Navigation, and Control Conference. Monterey, CA:AIAA, 2002.145-146 |
| [2] | Alighanbari M, Kuwata Y, How J P. Coordination and control of multiple UAVs with timing constraints and loitering. In:Proceedings of the 2003 American Control Conference. Denver, Colorado:IEEE, 2003.5311-5316 |
| [3] | Li C S, Wang Y Z. Protocol design for output consensus of portcontrolled Hamiltonian multi-agent systems. Acta Automatica Sinica, 2014, 40(3):415-422 |
| [4] | Duan H, Li P. Bio-inspired Computation in Unmanned Aerial Vehicles. Berlin:Springer-Verlag, 2014.143-181 |
| [5] | Duan H, Shao S, Su B, Zhang L. New development thoughts on the bioinspired intelligence based control for unmanned combat aerial vehicle. Science China Technological Sciences, 2010, 53(8):2025-2031 |
| [6] | Chi P, Chen Z J, Zhou R. Autonomous decision-making of UAV based on extended situation assessment. In:Proceedings of the 2006 AIAA Guidance, Navigation, and Control Conference and Exhibit. Colorado, USA:AIAA, 2006. |
| [7] | Ruz J J, Arelo O, Pajares G, de la Cruz J M. Decision making among alternative routes for uavs in dynamic environments. In:Proceedings of the 2007 IEEE Conference on Emerging Technologies and Factory Automation. Patras:IEEE, 2007.997-1004 |
| [8] | Jung S, Ariyur K B. Enabling operational autonomy for unmanned aerial vehicles with scalability. Journal of Aerospace Information Systems, 2013, 10(11):516-529 |
| [9] | Berger J, Boukhtouta A, Benmoussa A, Kettani O. A new mixed-integer linear programming model for rescue path planning in uncertain adversarial environment. Computers & Operations Research, 2012, 39(12):3420-3430 |
| [10] | Duan H B, Liu S. Unmanned air/ground vehicles heterogeneous cooperative techniques:current status and prospects. Science China Technological Sciences, 2010, 53(5):1349-1355 |
| [11] | Cruz Jr J B, Simaan M A, Gacic A, Jiang H, Letelliier B, Li M, Liu Y. Game-theoretic modeling and control of a military air operation. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(4):1393-1405 |
| [12] | Dixon W. Optimal adaptive control and differential games by reinforcement learning principles. Journal of Guidance, Control, and Dynamics, 2014, 37(3):1048-1049 |
| [13] | Semsar-Kazerooni E, Khorasani K. Multi-agent team cooperation:a game theory approach. Automatica, 2009, 45(10):2205-2213 |
| [14] | Gu D. A game theory approach to target tracking in sensor networks. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics, 2011, 41(1):2-13 |
| [15] | Duan H, Wei X, Dong Z. Multiple UCAVs cooperative air combat simulation platform based on PSO, ACO, and game theory. IEEE Aerospace and Electronic Systems Magazine, 2013, 28(11):12-19 |
| [16] | Turetsky V, Shinar J. Missile guidance laws based on pursuit-evasion game formulations. Automatica, 2003, 39(4):607-618 |
| [17] | Porter R, Nudelman E, Shoham Y. Simple search methods for finding a Nash equilibrium. Games and Economic Behavior, 2008, 63(2):642-662 |
| [18] | Chen X, Deng X, Teng S-H. Settling the complexity of computing twoplayer Nash equilibria. Journal of the ACM, 2009, 56(3):Article No. 14 |
| [19] | Kennedy J, Eberhart R. Particle swarm optimization. In:Proceedings of the 1st IEEE International Conference on Neural Networks. Perth, Australia:IEEE, 1995. 1942-1948 |
| [20] | Eberhart R, Kennedy J. A new optimizer using particle swarm theory. In:Proceedings of the 6th International Symposium on Micro Machine and Human Science. Nagoya:IEEE, 1995.39-43 |
| [21] | Higashitani M, Ishigame A, Yasuda K. Particle swarm optimization considering the concept of predator-prey behavior. In:Proceedings of the 2006 IEEE Congress on Evolutionary Computation. Vancouver, BC, Canada:IEEE, 2006.434-437 |
| [22] | Liu F, Duan H B, Deng Y M. A chaotic quantum-behaved particle swarm optimization based on lateral inhibition for image matching. Optik-International Journal for Light and Electron Optics, 2012, 123(21):1955-1960 |
| [23] | Edison E, Shima T. Genetic algorithm for cooperative UAV task assignment and path optimization. In:Proceedings of the 2008 AIAA Guidance, Navigation and Control Conference and Exhibit. Honolulu, Hawaii:AIAA, 2008. 340-356 |
| [24] | Duan H, Luo Q, Shi Y, Ma G. Hybrid particle swarm optimization and genetic algorithm for multi-UAV formation reconfiguration. IEEE Computational Intelligence Magazine, 2013, 8(3):16-27 |
| [25] | Liu G, Lao S Y, Tan D F, Zhou Z C. Research status and progress on anti-ship missile path planning. Acta Automatica Sinica, 2013, 39(4):347-359 |
| [26] | Duan H B, Yu Y X, Zhao Z Y. Parameters identification of UCAV flight control system based on predator-prey particle swarm optimization. Science China Information Sciences, 2013, 56(1):1-12 |
| [27] | Duan H, Li S, Shi Y. Predator-prey based brain storm optimization for DC brushless motor. IEEE Transactions on Magnetics, 2013, 49(10):5336-5340 |
| [28] | Pan F, Li X T, Zhou Q, Li W X, Gao Q. Analysis of standard particle swarm optimization algorithm based on Markov chain. Acta Automatica Sinica, 2013, 39(4):381-389 |
| [29] | Nash J F. Equilibrium points in n-person games. Proceedings of the National Academy of Sciences of the United States of America, 1950, 36(1):48-49 |
| [30] | Yu Qian, Wang Xian-Jia. Evolutionary algorithm for solving Nash equilibrium based on particle swarm optimization. Journal of Wuhan University (Natural Science Edition), 2006, 52(1):25-29(in Chinese) |
 2015, Vol.2
2015, Vol.2 



