2. Department of Mechanical Engineering, University of Bristol, BS8 1TR, UK
AMONG various modern control methodologies, optimal control has been well-recognized and successfully verified in some real-world applications[1],which is concerned with finding a control policy that drives a dynamical system to a desired reference in an optimal way,i.e.,a prescribed cost function is minimized. In general,the optimal control can be derived by using Pontryagin$'$s minimum principle,or by solving the Hamilton-Jacobi-Bellman (HJB) equation. Although mathematically elegant,traditional optimal control designs are obtained offline and impose the assumption on the complete knowledge of system dynamics[2]. To allow for uncertainties in system dynamics,adaptive control[3, 4] has been developed, where the unknown system parameters are online updated/estimated by using the tracking error,such that the tracking error convergence and the boundedness of the parameter estimates can be guaranteed. However,classical adaptive control methods are generally far from optimal.
With the wish to achieve adaptive optimal control,one may add optimality features to an adaptive controller,i.e.,to drive the adaptation by an optimality criterion. An alternative solution is to incorporate adaptive features into an optimal control design,e.g., improve the optimal control policy by means of the updated system parameters[2]. Recently,a bio-inspired method,reinforcement learning (RL)[5, 6, 7],that was developed in the computational intelligence and machine learning societies,has provided a means to design adaptive controllers in an optimal manner. Considering the similarities between optimal control and RL,Werbos[8] introduced an RL-based actor-critic framework,called approximate dynamic programming (ADP),where neural networks (NNs) are trained to approximately solve the optimal control problem based on the named value iteration (VI) method. A survey of ADP-based feedback control designs can be found in [9, 10, 11, 12].
The discrete/iterative nature of the ADP formulation lends itself naturally to the design of discrete-time (DT) optimal control[13, 14, 15]. However,the extension of the RL-based controllers to continuous-time (CT) systems entails challenges in proving stability and convergence for a model-free algorithm that can be solved online. Some of the existing ADP algorithms for CT nonlinear systems lacked a rigorous stability analysis[6, 16]. By incorporating NNs into the actor-critic structure,an offline method was proposed in [17] to find approximate solutions of optimal control for CT nonlinear systems. In [2, 18],an online integral RL technique was developed to find the optimal control for CT systems without using the system drift dynamics, which led to a hybrid continuous-time/discrete-time sampled data controller based on policy iteration (PI) with a two time-scale actor--critic learning process. This learning procedure was based on sequential updates of the critic (policy evaluation) NN and actor (policy improvement) NN. Thus,while one NN was tuned,the other one remained constant. Vamvoudakis and Lewis[19] further extended this idea by designing an improved online ADP algorithm called synchronous PI,which involved simultaneous tuning of both actor and critic NNs by minimizing the Bellman error,i.e.,both NNs were tuned at the same time by using the proposed adaptive laws to approximately solve the CT infinite horizon optimal control problem. To avoid the need for the complete knowledge of system dynamics in [19],a novel actor-critic-identifier architecture was proposed in [20],where an extra NN of the identifier was employed in conjunction with an actor-critic controller to identify the unknown system dynamics. Although the states of the identifier converged to their true values,the identifier NN weight convergence was not guaranteed. Moreover,the knowledge of the input dynamics was still required.
On the other hand,most of the ADP based optimal control methods have been developed to address the stabilization or regulation problem,and only a few results have been reported for optimal tracking control[21, 22, 23]. For these results,the key idea is to superimpose an optimal control that stabilizes the error dynamics at the transient stage in an optimal way under the assumption of a traditional steady-state tracking controller (e.g.,feedback linearization control,adaptive control). In [23], an observer was adopted to reconstruct unknown system states, while in [21] an adaptive NN identifier was used to online estimate unknown system dynamics. Although the obtained control input was ensured to be close to the optimal control within a small bound,it was not guaranteed that the NN identifier weights stayed bounded in a compact neighborhood of their ideal values. In this paper,we will provide a solution where the convergence of the identifier weights is guaranteed and the convergence of the critic NN weights to a nearly optimal control solution is shown. To the best of our knowledge,ADP-based optimal tracking control has rarely been designed for CT systems with unknown nonlinear dynamics and guaranteed parameter estimation convergence.
In this paper,we propose a new ADP algorithm for solving the optimal tracking control problem of nonlinear systems with unknown dynamics. Inspired by the work of [20, 21],the requirement of the complete or at least partial knowledge of system dynamics in the existing ADP algorithms for CT systems is eliminated. This is achieved by constructing an adaptive NN for the identifier of system dynamics; a novel adaptive law based on the parameter estimation error[24] is utilized such that,even in the presence of an NN approximation error,the identifier NN weights are guaranteed to converge to a small region around their true values under a standard persistent excitation (PE) condition or a slightly more relaxed singular value condition for a filtered regressor matrix. To achieve optimal tracking control,an adaptive steady-state control for maintaining desired tracking at the steady-state is augmented with an adaptive optimal control for stabilizing the tracking error dynamics in an optimal manner. To design such an optimal control,a critic NN is employed to online approximate the solution to the HJB equation. Thus,the optimal value function is obtained,which is then used to calculate the control action. The identifier parameters and critic NN weights are online updated continuously and simultaneously. In particular,a direct parameter estimation scheme is used to estimate NN weights; this is in contrast to the minimization of the Bellman error or the residual approximation error in the HJB equation by using least-squares[20] or the modified Levenberg-Marquardt algorithms[19]. We will also show that the identifier weight estimation error affects the critic NN convergence; the conventional PE condition or again a relaxed condition on a filtered regressor matrix is sufficient to guarantee parameter estimation convergence. To this end,a novel adaptation scheme based on the parameter estimation error that was originally proposed in our previous work [24] is employed for updating both identifier weights and critic NN weights; this may lead to fast convergence and provides an easy online-check of the required convergence condition[24]. Finally,the stability of the overall system and the uniform ultimate boundedness (UUB) of the identifier and critic weights are proved by using Lyapunov theory, and the obtained control guarantees the tracking of a desired trajectory,while also asymptotically converging to a small bound around the optimal policy.
The main contributions can be summarized as follows.
1) The optimal tracking control problem of nonlinear CT systems is studied by proposing a new critic-identifier based ADP control configuration. The actor NN is not necessary to prove the overall stability. Thus,instead of the triple-approximation structure, this introduces a simplified dual-approximation method. To achieve tracking control,a steady-state control is used in conjunction with an adaptive optimal control such that the overall control converges to the optimal solution within a small bound.
2) A novel adaptation design methodology based on the parameter estimation error is proposed such that the weights of both the identifier NN and critic NN are online updated simultaneously. With this framework,all these weights are 'directly' estimated with guaranteed convergence rather than updated to minimize the identifier error and Bellman error by using the gradient-based schemes (e.g.,least-squares in [20]). It is shown that the convergence of the identifier weights to their true values in a bounded sense is achieved,which is also important for the convergence of the optimal control.
The paper is organized as follows. Section II provides the formulation of the optimal control problem. Section III discusses the design of the identifier to accommodate unknown system dynamics. Section IV presents the adaptive tracking control design and the closed-loop stability analysis. Section V presents simulation examples that show the effectiveness of the proposed method,and Section VI gives some conclusions.
Ⅱ. PROBLEM FORMULATIONConsider a continuous-time nonlinear system as
| \begin{align} \label{eq1} \dot {x}=F(x,u), \end{align} | (1) |
This paper will address the optimal tracking control for system (1),i.e.,to find an adaptive controller $u$ which ensures that the system output $x$ tracks a given trajectory $x_d$ and fulfills the following infinite horizon cost function[21] (in a sub-optimal sense):
| \begin{align} \label{eq2} V^\ast (e(t))=\mathop {\min }\limits_{u(\tau )\in \Psi (\Omega )} \int_t^\infty {r(e(\tau ),u(\tau ))} {\rm d}\tau, \end{align} | (2) |
Remark 1. Many industrial processes can be modeled as system (1),such as missile systems[25],robotic manipulators[4] and biochemical processes[26]. Although some results[2, 11, 12, 19, 20] have been recently developed to address the optimal regulation problem of (partially unknown) system (1) by means of ADP,only a few results[21, 22, 25] have been reported concerning the tracking control of system (1). In [22],the plant system is assumed to be precisely known.
To facilitate the control design,the following assumption is made about system (1).
Assumption 1[27]. The function $F(x,u)$ in (1) is continuous and satisfies a locally Lipschitz condition such that (1) has a unique solution on the set $\Omega $ that contains the origin. The control action $u$ has a control-affine form as in [19, 20] with constant input gain $B$.
Since the dynamics of (1) are unknown,the optimal tracking control design presented in this paper can be divided into two steps as in [20, 21]:
1) Propose an adaptive identifier by using input-output data to reconstruct the unknown system dynamics for (1);
2) Design an adaptive optimal tracking controller based on the identified dynamics and ADP methods.
Ⅲ. ADAPTIVE IDENTIFIER BASED ON PARAMETER ESTIMATION ERRORIn this section,an adaptive identifier is established to reconstruct the unknown system dynamics using available input--output measurements. From Assumption 1,system (1) can be rewritten in the form of a recursive neural network (RNN)[21, 27, 28]:
| \begin{align} \label{eq3} \dot {x}=Ax+Bu+C^{\rm T}f(x)+\varepsilon, \end{align} | (3) |
To determine the unknown parameters $C$,we define the filtered variables $x_f$,$ u_f$,$f_f $ of $x$,$u$,$f$ as
| \begin{align} \label{eq4} \left\{ {\begin{array}{l} k\dot {x}_f +x_f =x,\mbox{ }x_f (0)=0,\\ k\dot {u}_f +u_f =u,\mbox{ }u_f (0)=0,\\ k\dot {f}_f +f_f =f,\mbox{ }f_f (0)=0,\\ \end{array}} \right. \end{align} | (4) |
Then for any positive scalar constant $\ell >0$,we define the filtered and 'integrated' regressor matrices $P_1 \in {\bf R}^{p\times p}$ and $Q_1 \in {\bf R}^{p\times n}$ as
| \begin{align} \label{eq5} \left\{ {\begin{array}{l} \dot {P}_1 =-\ell P_1 +f_f f_f^{\rm T} ,\mbox{ }P_1 (0)=0,\\ \dot {Q}_1 =-\ell Q_1 +f_f \left[{\frac{x-x_f }{k}-Ax_f -Bu_f } \right]^{\rm T},\mbox{ }Q_1 (0)=0,\\ \end{array}} \right. \end{align} | (5) |
| \begin{align} \label{eq6} M_1 =P_1 \hat {C}-Q_1, \end{align} | (6) |
Then the adaptive law for estimating $\hat {C}$ is provided by
| \begin{align} \label{eq7} \dot {\hat {C}}=-\Gamma _1 M_1, \end{align} | (7) |
Lemma 1[24]. Under the assumption that variables $x$ and $u$ in (3) are bounded,vector $M_1$ in (6) can be reformulated as $M_1 =-P_1 \tilde {C}+\psi_1 $ for bounded $\psi_1 (t)=-\int_0^t {{\rm e}^{-\ell (t-r)}f_f (r)\varepsilon _f^{\rm T} (r){\rm d}r} $,where $\tilde {C}=C-\hat {C}$ is the estimation error.
Proof. For the ordinary matrix differential~equation of (5),one can obtain its solution as[24]
| \begin{align} \label{eq8} \left\{ {\begin{array}{l} P_1 =\int_0^t {{\rm e}^{-\ell (t-r)}f_f (r)f_f^{\rm T} (r){\rm d}r} ,\\ Q_1 =\\ ~~~\int_0^t {{\rm e}^{-\ell (t-r)}f_f (r)\left[{\frac{x(r)-x_f (r)}{k}-Ax_f (r)-Bu_f (r)} \right]^{\rm T}{\rm d}r}. \\ \end{array}} \right. \end{align} | (8) |
| \begin{align} \label{eq9} \dot {x}_f =Ax_f +Bu_f +C^{\rm T}f_f +\varepsilon _f, \end{align} | (9) |
| \begin{align} \label{eq10} \dot {x}_f =\frac{x-x_f }{k}. \end{align} | (10) |
| \begin{align} \label{eq11} \frac{x-x_f }{k}=Ax_f +Bu_f +C^{\rm T}f_f+\varepsilon _f. \end{align} | (11) |
Then,(6) can be rewritten as
| \begin{align} \label{eq12} M_1 =P_1 \hat {C}-Q_1 =-P_1 \tilde {C}+\psi _1, \end{align} | (12) |
Moreover,to prove the parameter estimation convergence,we need to analyze the positive definiteness property of $P_1 $. Denote $\lambda_{\max } (\cdot )$ and $\lambda_{\min } (\cdot )$ as the maximum and minimum eigenvalues of the corresponding matrices, then we have the following lemma.
Lemma 2[24]. If the regressor function vector $f(x)$ defined in (3) is persistently excited[3],then the matrix $P_1 $ defined in (5) is positive definite,i.e.,its minimum eigenvalue $\lambda_{\min } (P_1 )>\sigma_1 >0$ with $\sigma_1 $ being a positive constant.
We refer to [24] for the detailed proof of Lemma 2.
Now,we have the following result.
Theorem 1. If $x$ and $u$ in (3) are bounded and the minimum eigenvalue of $P_1 $ satisfies $\lambda_{\min } (P_1 )>\sigma_1 >0$ for system (3) with the parameter estimation (7), then we have
1) For $\varepsilon =0$ (i.e.,no reconstruction error),the estimation error $\tilde {C}$ exponentially converges to zero;
2) For $\varepsilon \ne 0$ (i.e.,with bounded approximation error), the estimation error $\tilde {C}$ converges to a compact set around zero.
Proof. Consider the Lyapunov function candidate as $V_1 =\frac{1}{2}{\rm tr} ( {\tilde {C}^{\rm T}\Gamma _1^{-1} \tilde {C}})$,then the derivative $\dot {V}_1 $ is obtained from (7) as
| \begin{align} \label{eq13} \dot {V}_1 ={\rm tr} ( {\tilde {C}^{\rm T}\Gamma _1^{-1} \dot {\tilde {C}}} )=-{\rm tr} ( {\tilde {C}^{\rm T}P_1 \tilde {C}} )+{\rm tr} ( {\tilde {C}^{\rm T}\psi _1 } ). \end{align} | (13) |
1) In case that $\varepsilon =0$ and thus $\psi _1 =0$,(13) is reduced to
| \begin{align} \label{eq14} \dot {V}_1 =-{\rm tr} ( {\tilde {C}^{\rm T}P_1 \tilde {C}} )\le -\sigma _1 || {\tilde {C}} ||^2\le -\mu _1 V_1, \end{align} | (14) |
2) In case that there is a bounded approximation error $\varepsilon \ne 0$,(13) can be further presented as
| \begin{align} \label{eq15} \dot {V}_1 =-{\rm tr} ( {\tilde {C}^{\rm T}P_1 \tilde {C}} )+{\rm tr} ( {\tilde {C}^{\rm T}\psi _1 } )\le -|| {\tilde {C}} || ( {\tilde {\sigma }_1 \sqrt {V_1 } -\varepsilon _{1\psi } } ) \end{align} | (15) |
Remark 2. For adaptive law (7),variable $M_1 $ of (6) obtained based on $P_1$,$Q_1$ by (5) contains the information on the weight estimation error $P_1 \tilde {C}$ as shown in (12), where the residual error $\psi _1 $ will vanish for vanishing NN approximation error $\varepsilon \to 0$. It is well known that $\varepsilon \to 0$ holds for sufficiently large hidden layer nodes in identifier (3),i.e.,$p\to +\infty $. Thus $M_1 $ can be used to drive parameter estimation (7). Consequently,parameter estimation $\hat {C}$ can be directly obtained without using an observer/predictor error in comparison to [20, 21] (see Theorem 1 in [20, 21]).
Remark 3. Lemma 2 shows that the required condition (i.e.,$\lambda _{\min } (P_1 )>\sigma _1 >0)$ for the parameter estimation convergence in this paper can be fulfilled under a conventional PE condition[3]. In general,the direct online validation of the PE condition is difficult in particular for a nonlinear system. To this end,Lemma 2 provides a numerically verifiable way to online validate the required convergence condition of the novel adaptation law (7),i.e.,by calculating the minimum eigenvalue of matrix $P_1 $ to test $\lambda_{\min } (P_1 )>\sigma _1 >0$. This condition does not necessarily imply the PE condition of $f(x)$. It is also to be noticed that the PE condition of $f(x)$ can be suitably weakened when a well-designed control is imposed[24, 29],e.g.,transformed into an a priori verifiable 'sufficient richness (SR)' requirement on the command reference.
Ⅳ. ADAPTIVE APPROXIMATE OPTIMAL TRACKING CONTROLAs shown in Section III,the unknown weight parameter $C$ can be online estimated. Without loss of generality,we assume that there is an unavoidable approximation error $\varepsilon $ in (3) such that the estimated weight matrix $\hat {C}$ would converge to a compact set around its true value $C$. In this case,system can be rewritten as
| \begin{align} \label{eq16} \dot {x}=Ax+Bu+\hat {C}^{\rm T}f(x)+\varepsilon +\varepsilon _N, \end{align} | (16) |
To achieve optimal tracking control,it is noted that the overall control $u$ can be composed of two parts as $u=u_s +u_e $,where $u_s $ is the adaptive steady-state control used to maintain the tracking error close to zero at the steady-state stage,and $u_e $ is the adaptive optimal control designed to stabilize the tracking error dynamics in the control transient in an optimal manner[21, 22, 25].
Consider the tracking error as $e=x-x_d $,so that
| \begin{align} \label{eq17} \begin{array}{c} \dot {e}=Ax+Bu+\hat {C}^{\rm T}f(x)-\dot {x}_d +\varepsilon +\varepsilon _N . \end{array} \end{align} | (17) |
| \begin{align} \label{eq18} u_s =B^\otimes (\dot {x}_d -Ax_d -\hat {C}^{\rm T}f(x_d )), \end{align} | (18) |
It is shown that $u_s$ depends on the available variables $x_d $, $\dot {x}_d $,$A$,$\hat {C}$,and thus can be implemented based on identifier (3) with adaptive law (7). Substituting (18) into (17),the tracking error dynamics can be rewritten as
| \begin{align} \label{eq19} \dot {e}=Ae+\hat {C}^{\rm T}\left[{f(x)-f(x_d )} \right]+Bu_e +\varepsilon +\varepsilon _N +\varepsilon _\varphi, \end{align} | (19) |
As shown above,by using the adaptive steady-state control $u_s$ in (18),the error dynamics can be further presented as (9),which is not necessarily stable,in particular for a system with identifier error $\varepsilon +\varepsilon _N $. In this sense, the tracking problem of system (16) can be reduced into the regulation problem of (19). Hence,the adaptive optimal control $u_e$ will be designed to stabilize the tracking error dynamics (19) in an approximately optimal manner.
In this case,the optimal value function (2) for system (1) can be reformulated using $u_e $ from system (19) to provide the value function
| \begin{align} \label{eq20} V(e(t))=\int_t^\infty {r(e(\tau ),u_e (e(\tau )))} {\rm d}\tau, \end{align} | (20) |
Definition 1[17]. A control policy $\mu (e)$ is defined as admissible with respect to (20) on a compact set $\Omega $,denoted by $\mu (e)\in \Psi (\Omega )$. If $\mu (e)$ is continuous on $\Omega $,$\mu (0)=0$,$\mu (e)=u(e)$ stabilizes (19) on $\Omega $,and $V(e)$ is finite $\forall e\in \Omega $.
The remaining problem can be formulated as: given the CT error system (19) with the admissible control set $\mu (e)\in \Psi (\Omega )$ and the infinite horizon cost function (20),find an admissible control policy $u_e (e)\in \mu (e)$ such that cost (20) associated with system (19) is minimized.
For this purpose,we define the Hamiltonian of system (19) as
| \begin{align} %\label{eq21} %\begin{split} H(e,u_e ,V) =&V_e^{\rm T} [{Ae+\hat {C}^{\rm T}(f(x)-f(x_d ))+Bu_e} +\notag\\ &{\varepsilon +\varepsilon _N +\varepsilon _\varphi }]+e^{\rm T}Qe+u_e^{\rm T} Ru_e, %\end{split} \end{align} | (21) |
The optimal cost function $V^\ast (e)$ is defined as
| \begin{align} \label{eq22} V^\ast (e)=\mathop {\min }\limits_{u_e \in \Psi (\Omega )} \left( {\int_t^\infty {r(e(\tau ),u_e (e(\tau )))} {\rm d}\tau } \right), \end{align} | (22) |
| \begin{align} \label{eq23} 0=\mathop {\min }\limits_{u_e \in \Psi (\Omega )} \left[{H(e,u_e^\ast ,V^\ast )} \right]. \end{align} | (23) |
| \begin{align} \label{eq24} u_e^\ast =-\frac{1}{2}R^{-1}B^{\rm T}\frac{\partial V^\ast (e)}{\partial e}, \end{align} | (24) |
Remark 4. In order to find the optimal control (24),one needs to solve the HJB equation (23) for the value function $V^\ast (e)$ and then substitute the solution into (24) to obtain the optimal control $u_e^\ast $. For linear systems,considering a quadratic cost functional,the equivalent of the HJB equation is the well known Riccati equation[1]. However,for nonlinear systems,the HJB equation (23) is a nonlinear partial differential equation (PDE) which is difficult to solve.
In the literature,there are a number of results concerning the optimal control for (19) in terms of critic-actor based ADP schemes,where two NNs,i.e.,a critic NN and an actor NN,are employed to approximate the value function and its corresponding policy. However,some of them run in an offline manner[17] and/or require at least partial knowledge of system dynamics[2, 18, 19, 20, 22]. In the following,an online adaptive algorithm will be proposed to derive the optimal control solution for system (19) using the NN identifier introduced in the previous section and another critic NN for approximating the value function of the HJB equation (23). Instead of sequentially updating the critic and actor NNs[2, 18],both networks are updated simultaneously in real time,and thus lead to the synchronous online implementation.
A. Value Function Approximation via NNAssuming the optimal value function is continuous and defined on compact sets,then a single-layer NN can be used to approximate it[19],such that the solution $V^\ast (e)$ and its derivative $\partial V^\ast (e)/\partial e$ with respect to $e$ can be uniformly approximated by
| \begin{align} \label{eq25} V^\ast (e)=W^{\ast \rm T}\Phi (e)+\varepsilon _1, \end{align} | (25) |
| \begin{align} \label{eq26} \frac{\partial V^\ast (e)}{\partial e}=\nabla \Phi ^{\rm T}W^\ast +\nabla \varepsilon _1, \end{align} | (26) |
Some standard NN assumptions that will be used throughout the remainder of this paper are summarized here.
Assumption 2[17, 19, 20, 21]. The ideal NN weights $W^\ast $ are bounded by a positive constant $W_N $,i.e., $\left\| {W^\ast } \right\|\le W_N $; the NN activation function $\Phi (\cdot )$ and its derivative $\nabla \Phi (\cdot )$ with respect to argument $e$ are bounded,e.g.,$\left\| {\nabla \Phi } \right\|\le \phi _M $; and the function approximation error $\varepsilon _1 $ and its derivative $\nabla \varepsilon _1 $ with respect to $e$ are bounded,e.g.,$\left\| {\nabla \varepsilon _1 } \right\|\le \phi _\varepsilon $.
In a practical application,the NN activation functions $\left\{ {\Phi _i (e):i=1,\cdots ,l} \right\}$ can be selected so that as $l\to +\infty $,$\Phi (e)$ provides a complete independent basis for $V^\ast (e)$. Then using Assumption 2 and the Weierstrass higher-order approximation theorem,both $V^\ast (e)$ and $\partial V^\ast (e)/\partial e$ can be uniformly approximated by NNs in (25) and (26),i.e.,as $l\to +\infty $,the approximation errors $\varepsilon _1 \to 0 $,$\nabla \varepsilon _1 \to 0$ as shown in [17, 19]. Then the critic NN $\hat {V}(e)$ that approximates the optimal value function $V^\ast (e)$ is given by
| \begin{align} \label{eq27} \hat {V}(e)=\hat {W}^{\rm T}\Phi (e), \end{align} | (27) |
In this case,one may obtain the approximated optimal control as
| \begin{align} \label{eq28} \hat {u}_e =-\frac{1}{2}R^{-1}B^{\rm T}\frac{\partial \hat {V}(e)}{\partial e}=-\frac{1}{2}R^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\hat {W}, \end{align} | (28) |
| \begin{align} \label{eq29} u=u_s +\hat {u}_e \end{align} | (29) |
Consider that the ideal optimal control $u_e^\ast $ can be determined based on (24) and (26) as
| \begin{align} \label{eq30} u_e^\ast =-\frac{1}{2}R^{-1}B^{\rm T}\frac{\partial V^\ast (e)}{\partial e}\mbox{=}-\frac{1}{2}R^{-1}B^{\rm T}( {\nabla \Phi ^{\rm T}W^\ast +\nabla \varepsilon _1 }), \end{align} | (30) |
| \begin{align} \dot {e}=&Ae+\hat {C}^{\rm T}\left[{f(x)-f(x_d )} \right]+Bu_e +\varepsilon +\varepsilon _N +\varepsilon _\varphi =\notag\\ &Ae+\hat {C}^{\rm T}\left[{f(x)-f(x_d )} \right]+B[ {-\frac{1}{2}R^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\hat {W}}+\notag\\ &{\frac{1}{2}R^{-1}B^{\rm T}( {\nabla \Phi ^{\rm T}W^\ast +\nabla \varepsilon _1 } )}]+Bu_e^\ast+\varepsilon +\varepsilon _N +\varepsilon _\varphi \notag\\ &=Ae+\hat {C}^{\rm T}\left[{f(x)-f(x_d )} \right]+\frac{1}{2}BR^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\tilde {W}+\notag\\ &Bu_e^\ast+\frac{1}{2}BR^{-1}B^{\rm T}\nabla \varepsilon _1 +\varepsilon +\varepsilon _N +\varepsilon _\varphi. \end{align} | (31) |
Remark 5. Since the overall control (29) is derived using the steady-state control (18) and the approximate optimal control (28) that depends on the estimated optimal value function $\nabla \Phi ^{\rm T}\hat {W}$,the critic NN in (27) can be used to determine the control action without using another NN as the actor in [19, 20, 21]. This can reduce the computational cost and improve the learning process. However,alternatively,a separate actor NN, e.g.,$\nabla \Phi ^{\rm T}\hat {W}_a $,may be used in a similar way for producing the approximated optimal control action $\hat {u}_e =-\frac{1}{2}R^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\hat {W}_a $ as that shown in [19, 20, 21].
B. Adaptive Law for Critic NNThe problem now is to update the critic NN weights $\hat {W}$, such that $\hat {W}$ converge to a small bounded region around the ideal values $W^\ast $. To derive the adaptive law,we denote $f_d =f(x_d )$,substitute (26) into Hamiltonian function (21),and thus rewrite the HJB equation (23) as
| \begin{align} &0=H(e,u_e ,V^\ast )=W^{\ast {\rm T}}\nabla \Phi [{Ae+\hat {C}^{\rm T}(f-f_d )+Bu_e }]+\notag\\ &\qquad \qquad e^{\rm T}Qe+u_e^{\rm T} Ru_e +\varepsilon _{HJB}, \end{align} | (32) |
To facilitate the design of the adaptive law,we denote the known terms in (32) as $\Xi =\nabla \Phi \left[{Ae+\hat {C}^{\rm T}(f-f_d )+Bu_e } \right]$ and $\Theta =e^{\rm T}Qe+u_e^{\rm T} Ru_e $,and then represent (32) as
| \begin{align} \label{eq33} \Theta =-W^{\ast {\rm T}}\Xi -\varepsilon _{HJB}. \end{align} | (33) |
Remark 6. It is shown in (32) that the residual HJB equation error $\varepsilon _{HJB} $ is due to the critic NN approximation error $\nabla \varepsilon _1 $ in (26),the identifier error $\varepsilon +\varepsilon _N $ in (16) and the matching condition error $\varepsilon _\varphi $. As claimed in [17, 19],the critic NN approximation error $\nabla \varepsilon _1 $ converges uniformly to zero as the number of hidden layer nodes increases,i.e.,$\nabla \varepsilon _1 \to 0$ as long as $l\to +\infty $. That is,$\forall \mu >0$,$\exists N(\mu ):\sup \left\| {\nabla \varepsilon _1 } \right\|\le \mu $. Moreover,in case that there is no NN approximation error in (3),i.e., $\varepsilon =0$,the effect of the identifier error $\varepsilon _N $ in (16) will vanish (i.e.,$\varepsilon _N \to 0$ as $p\to +\infty )$ because $\tilde {C}\to 0$ holds for $\varepsilon =0$ as proved in Theorem 1 for bounded state $x$ and control input $u$. Finally,the fact $\varepsilon _\varphi =0$ is also true under the matching condition in (19). Consequently,if there are no approximation errors $\varepsilon $ in identifier (16) and $\nabla \varepsilon _1 $ in critic NN (26),and the matching condition holds,the residual error in (33) is null,i.e., $\varepsilon _{HJB} =0$.
Remark 7. Some available ADP based optimal controls are designed to online update the critic NN weights $\hat {W}$ by minimizing the squared residual Bellman error in the approximated HJB equation[19, 20, 21, 23],where the Least-squares[20] or modified Levenberg-Marquardt algorithms[19] are employed. In the following,we will extend our previous results[24] to design the adaptive law to directly estimate unknown critic NN weights $W^\ast $ based on (33) rather than to reduce the Bellman error.
Similar to Section III,we define the auxiliary filtered regressor matrix $P_2 \in {\bf R}^{l\times l}$ and vector $Q_2 \in {\bf R}^l$ as
| \begin{align} \label{eq34} \left\{ {\begin{array}{l} \dot {P}_2 =-\ell P_2 +\Xi \Xi ^{\rm T},\mbox{ }P_2 (0)=0,\\ \dot {Q}_2 =-\ell Q_2 +\Xi \Theta ,\mbox{ }Q_2 (0)=0,\\ \end{array}} \right. \end{align} | (34) |
| \begin{align} \label{eq35} \left\{ {\begin{array}{l} P_2 =\int_0^t {{\rm e}^{-\ell (t-r)}\Xi (r)\Xi ^{\rm T}(r){\rm d}r},\\ Q_2 =\int_0^t {{\rm e}^{-\ell (t-r)}\Xi (r)\Theta (r){\rm d}r}. \\ \end{array}} \right. \end{align} | (35) |
| \begin{align} \label{eq36} M_2 =P_2 \hat {W}+Q_2, \end{align} | (36) |
By substituting (33) into (35),we have $Q_2 =-P_2 W^\ast +\psi _2 $ with $\psi _2 =-\int_0^t {{\rm e}^{-\ell (t-r)}\varepsilon _{HJB} (r)\Xi (r){\rm d}r} $ being a bounded variable for bounded state $x$ and control $u$,e.g.,$\left\| {\psi _2 } \right\|\le \varepsilon _{2\psi } $ for some $\varepsilon _{2\psi } >0$. In this case,(36) can be rewritten as
| \begin{align} \label{eq37} M_2 =P_2 \hat {W}+Q_2 =-P_2 \tilde {W}+\psi _2, \end{align} | (37) |
Then the adaptive law for estimating $\hat {W}$ is provided by
| \begin{align} \label{eq38} \dot {\hat {W}}=-\Gamma _2 M_2, \end{align} | (38) |
Similar to Section III,the condition that $\lambda _{\min } (P_2 )>\sigma _2 >0$ is needed if one desires to precisely estimate the unknown critic NN weights $W^\ast $ so that the approximated value function (27) converges to its true value (25). As shown in [19, 20],a small probing noise can be added to the control input to retain the PE condition if this condition is not satisfactory. This implies $\lambda _{\min } (P_2 )>\sigma _2 >0$,as stated in Lemma 3.
Lemma 3[24]. If the regressor function vector $\Xi $ defined in (33) is persistently excited,then matrix $P_2 $ defined in (35) is positive definite,i.e.,its minimum eigenvalue $\lambda _{\min } (P_2 )>\sigma _2 >0$.
Then we have the following theorem.
Theorem 2. For the critic NN adaptive law (38) with regressor vector $\Xi $ satisfying $\lambda _{\min } (P_2 )>\sigma _2 >0$ and for bounded state $x$ and control $u$,one has
1) For $\varepsilon _{HJB} =0$ (i.e.,no NN approximation errors), the estimation error $\tilde {W}$ exponentially converges to zero;
2) For $\varepsilon _{HJB} \ne 0$ (i.e.,with bounded approximation errors),the estimation error $\tilde {W}$ converges to a bounded set around zero.
Proof. Consider the Lyapunov function candidate as $V_2 =\frac{1}{2}\tilde {W}^{\rm T}\Gamma _2^{-1} \tilde {W}$,then the derivative $\dot {V}_2 $ can be calculated along as
| \begin{align} \label{eq39} \dot {V}_2 =\tilde {W}^{\rm T}\Gamma _2^{-1} \dot {\tilde {W}}=-\tilde {W}^{\rm T}P_2 \tilde {W}+\tilde {W}^{\rm T}\psi _2. \end{align} | (39) |
1) In case that $\varepsilon _{HJB} =0$,i.e.,$\psi _2 =0$,thus (39) can be reduced as
| \begin{align} \label{eq40} \dot {V}_2 =-\tilde {W}^{\rm T}P_2 \tilde {W}\le -\sigma _2 || {\tilde {W}} ||^2\le -\mu _2 V_2, \end{align} | (40) |
2) In case that there are bounded approximation errors,i.e., $\varepsilon _{HJB} \ne 0$,(39) can be written as
| \begin{align} \label{eq41} \dot {V}_2 =-\tilde {W}^{\rm T}P_2 \tilde {W}+\tilde {W}^{\rm T}\psi _2 \le -|| {\tilde {W}} || ( {\tilde {\sigma }_2 \sqrt {V_2 } -\varepsilon _{2\psi } } ) \end{align} | (41) |
Now,we summarize the main results of this paper as follows.
Theorem 3. For system (3) with controls (18),(28) and adaptive laws (7),(38) being used,if the initial control action is chosen to be admissible and regressor vectors $f$ and $\Xi $ satisfy $\lambda _{\min } (P_1 )>\sigma _1 >0$ and $\lambda _{\min } (P_2 )>\sigma _2 >0$,then the following semi-global results hold:
1) In the absence of approximation errors,the tracking error $e$ and the parameter estimation errors $\tilde {C}$ and $\tilde {W}$ converge to zero,and adaptive control $\hat {u}_e$ in (28) converges to its optimal solution $u_e^\ast $ in (28),i.e.,$\hat {u}_e \to u_e^\ast $ if $\nabla \varepsilon _1 =0$.
2) In the presence of approximation errors,the tracking error $e$ and the parameter estimation errors $\tilde {C}$ and $\tilde {W}$ are uniformly ultimately bounded,and the adaptive control $\hat {u}_e $ in (28) converges to a small bound around its optimal solution $u_e^\ast $ in (24),i.e.,$\left\| {\hat {u}_e -u_e^\ast } \right\|\le \varepsilon _u $ for a small positive constant $\varepsilon _u $.
Please refer to Appendix for the detailed proof of Theorem 3.
Ⅴ. SIMULATIONSIn this section,a numerical example is provided to demonstrate the effectiveness of the proposed approach. Consider the following nonlinear continuous-time system
| \begin{align} \label{eq42} \left\{ {\begin{array}{l} \dot {x}_1 =-x_1 +x_2,\\ \dot {x}_2 =-0.5x_1 -0.5x_2 (\mbox{1}-(\cos (2x_1 )+2)^2)+\\ \quad\cos (2x_1)+2u. \\ \end{array}} \right. \end{align} | (42) |
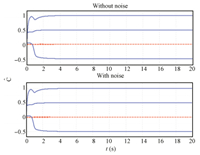
It is assumed that system dynamics are partially unknown,and we first use identifier (3) to reconstruct system dynamics with $A=\left[{{\begin{array}{*{20}c} {-1} \hfill & 1 \hfill \\ {-0.5} \hfill & 0 \hfill \\ \end{array} }} \right]$,$B\mbox{=}\left[{\begin{array}{l} \mbox{0} \\ \mbox{2} \\ \end{array}} \right]$ being known matrices,$C\mbox{=}\left[ {{\begin{array}{*{20}c} 0 \hfill & 0 \hfill & 0 \hfill \\ {-0.5} \hfill & {0.5} \hfill & 1 \hfill \\ \end{array} }} \right]^{\rm T}$ is the unknown identifier weights to be estimated, and the activation function is chosen as $f(x)\mbox{=}\left[{x_2, x_2 (\cos (2x_1 )+2)^2,\cos (2x_1 )} \right]^{\rm T}$. The parameters for simulation are set as $k=0.001$,$\ell =1$,$\Gamma _1 =350$. The initial weight parameter is set as $\hat {C}(0)\mbox{=}0$. Two different scenarios are investigated,the adaptive algorithm without and with injection of additional noise. The noise has a uniform distribution and a maximal amplitude of 0.1 induced at the measurements for $x_1 $ and $x_2 $. It is removed after a duration of 4 seconds. Fig. 1 shows the profile of the estimated identifier weights $\hat {C}$ with adaptive law (7),where one may find that the identifier weight estimation converges to their true value $C$ after a 3.5 second transient without noise. It is evident that the algorithm with noise injection converges slightly faster.
|
Download:
|
| Fig. 1. Convergence of identifier parameters $\hat {C}$. | |
In the following,the control performance will be verified. For this purpose,the adaptive steady-state control (18) for system (42) to maintain the steady-state performance can be written as
| \begin{align} %\label{eq43} %\begin{split} u_s &=\left[0 ,\frac{1}{2}\right] \Big( \Big [{\begin{array}{c} \cos (t) \\ \cos (t)-\sin (t) \\ \end{array}} \Big]-\notag\\ &\Big [{{\begin{array}{*{20}c} {-1} \hfill & 1 \hfill \\ {-0.5} \hfill & 0 \hfill \\ \end{array} }} \Big]\Big[{\begin{array}{c} \sin (t) \\ \cos (t)+\sin (t) \\ \end{array}} \Big] -\notag\\ & \hat {C}^{\rm T}\left[{\begin{array}{c} \cos (t)+\sin (t) \\ (\cos (t)-\sin (t))(\cos (2\sin (t))+2)^2 \\ \cos (2\sin (t))\\ \end{array}} \right] \Big). %\end{split} \end{align} | (43) |
To this end,following [19, 32],the optimal value function and the associated optimal control for system (42) are
| \begin{align} \label{eq44} V^\ast (e)=\frac{1}{2}e_1^2 +e_2^2 \quad \text{and} \quad u_e^\ast =-\frac{1}{2}R^{-1}B^{\rm T}\frac{\partial V^\ast (e)}{\partial e}=-2e_2. \end{align} | (44) |
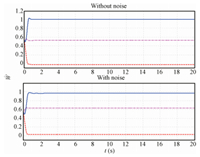
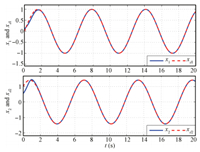
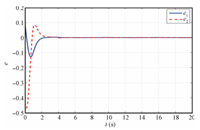
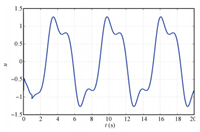
Similar to [19, 20],we select the activation function for the critic NN as $\Phi (e)=[e_1^2 ,e_1 e_2 ,e_2^2]^{\rm T}$,then the optimal weights $W^\ast =[0.5,0,1]^{\rm T}$ can be derived. Note that only the last non-zero coefficient $W_3^\ast =1$ affects the closed loop. The time trace for the online estimation of the critic NN weights $\hat {W}$ is shown in Fig. 2; this indicates that $\hat {W}$ converges in about 1.5 seconds. In particular, $\hat {W}_2 $ and $\hat {W}_3 $ converge close to its optimal value of 1 and 0,while $\hat {W}_1 $ for the noise induced case carries a larger error. $\hat {W}_1 $ does not affect the closed loop behavior,but has influence on the value function estimate. This means that the designed adaptive optimal control (28) converges close to its optimal control action in (44). An error in the weights is to be expected as $\varepsilon _\varphi \ne 0$. The novel identifier and critic NN weight update laws (7) and (38), based on the information of the parameter estimation error,lead to faster convergence of weights compared to [19]. Moreover,for the noise-free case,the system states for tracking the given external command are shown in Fig. 4,the tracking error profile is given in Fig. 5,and the associated control action is provided in Fig. 6. The noise induced case provides again very similar trajectories,which are not displayed here for space reasons.
|
Download:
|
| Fig. 2. Convergence of critic NN weights $\hat {W}$. | |
|
Download:
|
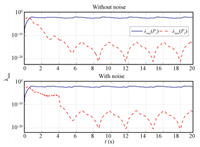
| Fig. 3. Excitation conditions $\lambda_{\min } (P_1 )$ and $\lambda _{\min } (P_2 )$. | |
|
Download:
|
| Fig. 4. Evaluation of tracking performance. | |
|
Download:
|
| Fig. 5. Convergence of tracking error $e=x-x_d $. | |
|
Download:
|
| Fig. 6. Control action profile $u$. | |
A critical issue in using the proposed adaptive laws (7) and (38) is to ensure sufficient excitation of regressor vectors $f(x)$ and $\Xi $. This condition can be fulfilled in the studied system as shown in Fig. 3,where the online evolutions of $\lambda _{\min } (P_1 )$ and $\lambda _{\min } (P_2 )$ are provided. The scalar $\lambda _{\min } (P_1 )$ remains positive at all time. The value of $\lambda _{\min } (P_2 )$ is sufficiently large till the time instant of 4 second when the noise is removed for the noise induced case; $\lambda _{\min } (P_2 )$ for the noise-free case remains sufficiently large until the time instant of 2 second,i.e.,after the NN weight convergence is obtained (See Figs. 1 and 2).
Ⅵ. CONCLUSIONSAn adaptive optimal tracking control is proposed for a class of continuous-time nonlinear systems with unknown dynamics. To achieve the optimal tracking control,an adaptive steady-state control for maintaining the desired steady-state tracking performance is accomplished with an adaptive optimal control for stabilizing the tracking error dynamics at transient stage in an optimal manner. To eliminate the need for precisely known system dynamics, an adaptive identifier is used to estimate the unknown system dynamics. A critic NN is used to online learn the approximate solution of the HJB equation,which is then used to provide the approximately optimal control action. Novel adaptive laws based on the parameter estimation error are developed for updating the unknown weights in both identifier and critic NN,such that the online learning of identifier and the optimal policy is achieved simultaneously. The PE conditions or more relaxed filtered regressor matrix conditions are required to ensure the error convergence to a bounded region around the optimal control and stability of the closed-loop system. Simulation results demonstrate the improved performance of the proposed method.
APPENDIXProof of Theorem 3. Consider the Lyapunov function as
| \begin{align} &V=V_1 +V_2 +V_3 +V_4 =\notag\\ &\qquad \frac{1}{2}{\rm tr} ( {\tilde {C}^{\rm T}\Gamma _1^{-1} \tilde {C}} )+\frac{1}{2}\tilde {W}^{\rm T}\Gamma _2^{-1} \tilde {W}+\Gamma e^{\rm T}e +KV^\ast (e)+\Sigma \psi _2^{\rm T} \psi _2, \end{align} | (A1) |
Thus,consider inequality $ab\le a^2\eta /2+b^2/2\eta $ for $\eta >0$,then derivative $\dot {V}_1 $ along (7) is derived as
| \begin{align} %\begin{split} %\label{eq46} \dot {V}_1 &={\rm tr} ( {\tilde {C}^{\rm T}\Gamma _1^{-1} \dot {\tilde {C}}} )=-{\rm tr} ( {\tilde {C}^{\rm T}P_1 \tilde {C}} )+{\rm tr}( {\tilde {C}^{\rm T}\psi _1 } )\le \notag\\ & - ( {\sigma _1 -1/2\eta } )|| {\tilde {C}} ||^2+\eta \varepsilon _{1\psi }^2 /2, %\end{split} \end{align} | (A2) |
| \begin{align} %\begin{split} %\label{eq47} \dot {V}_2 &=\tilde {W}^{\rm T}\Gamma _2^{-1} \dot {\tilde {W}}=-\tilde {W}^{\rm T}P_2 \tilde {W}+\tilde {W}^{\rm T}\psi _2 \le\notag\\ & - ( {\sigma _2 -1/2\eta } )|| {\tilde {W}} ||^2+\eta || {\psi _2 } ||^2/2. %\end{split} \end{align} | (A3) |
| \begin{align} \begin{split} \label{eq48} \dot {V}_3 &=2\Gamma e^{\rm T}\dot {e}+K ( {-e^{\rm T}Qe-u_e^{\ast \rm T} Ru_e^\ast } ) =\\ &2e^{\rm T}\Gamma \Bigg[{Ae+\hat {C}^{\rm T}\left({f-f_d} \right)+\frac{1}{2}BR^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\tilde {W}+Bu_e^\ast }+\\ &{\frac{1}{2}BR^{-1}B^{\rm T}\nabla \varepsilon _1 +\varepsilon +\varepsilon _N +\varepsilon _\varphi } \Bigg]+K ( {-e^{\rm T}Qe-u_e^{\ast {\rm T}} Ru_e^\ast }) \le\\ & -\left[{K\lambda _{\min } (Q)-\Gamma ( {4+2\left\| A \right\|+|| {\hat {C}} ||^2\kappa ^2} )} \right]\left\| e \right\|^2+\\ &\frac{1}{2}\Gamma || {BR^{-1}B^{\rm T}\nabla \Phi ^{\rm T}} ||^2|| {\tilde {W}}||^2-\left( {{K}\lambda _{\min } (R)-\Gamma \left\| B \right\|^2} \right)\left\| {u_e^\ast } \right\|^2 +\\ & \frac{1}{2}\Gamma || {BR^{-1}B^{\rm T}} ||\left( {\nabla \varepsilon _1 } \right)^{\rm T}\nabla \varepsilon _1 +\Gamma \varepsilon ^{\rm T} \varepsilon +\Gamma \varepsilon _N^{\rm T} \varepsilon _N +\Gamma \varepsilon _\varphi ^{\rm T} \varepsilon _\varphi. \end{split} \end{align} | (A4) |
It is evident that $\dot {\psi }_2 =-\ell \psi _2 +\Xi \varepsilon _{HJB} \mbox{ }$. Hence,similar to the parameter $\eta >0$,parameter $\mu >0$ is introduced to compute an upper bound of the derivative of $V_4 =\Sigma \psi _2^{\rm T} \psi _2 $ as
| \begin{align} \label{eq49} \begin{split} \dot {V}_4 &=2\Sigma \psi _2^{\rm T} \dot {\psi }_2 =\\ &2\Sigma \psi _2^{\rm T} \Bigg \{-\ell \psi _2 +\Xi \Big [W^{\ast {\rm T}}\nabla \Phi \left( {\varepsilon _N +\varepsilon _\varphi +\varepsilon } \right) +\\ & \nabla \varepsilon _1 \Big( {Ae+\hat {C}^{\rm T}(f-f_d )+Bu_e +\varepsilon +\varepsilon _N +\varepsilon _\varphi } \Big)\mbox{ } \Big]\Bigg \} \le\\ & -\Sigma (2\ell -5\mu )\left\| {\psi _2 } \right\|^2+\frac{1}{\mu }\Sigma || {\Xi (W^{\ast {\rm T}}\nabla \Phi +\nabla \varepsilon _1 )\left( {\varepsilon _\varphi +\varepsilon } \right))} ||^2+\\ &\frac{1}{\mu }\Sigma || {\Xi \nabla \varepsilon _1 \hat {C}^{\rm T}(f-f_d ))} ||^2 \mbox{+ }\frac{1}{\mu }\Sigma || {\Xi \nabla \varepsilon _1\frac{1}{2}BR^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\hat {W}} ||^2+\\ & \frac{1}{\mu }\Sigma \left\| {\Xi \nabla \varepsilon _1 Ae} \right\|^2 +\frac{1}{\mu }\Sigma || {\Xi (W^{\ast {\rm T}}\nabla \Phi +\nabla \varepsilon _1 )} ||^2\left\| {\varepsilon _N } \right\|^2. \end{split} \end{align} | (A5) |
Considering that $\varepsilon _N =\tilde {C}f(x)$,we have
| \begin{align} &\dot {V}=\dot {V}_1 +\dot {V}_2 +\dot {V}_3 +\dot {V}_4 \le\notag\\ &\qquad -\left[{\sigma _1 -\frac{1}{2\eta }- \Big ( {\Gamma +\frac{1}{\mu }\Sigma || {\Xi (W^{\ast {\rm T}}\nabla \Phi +\nabla \varepsilon _1 )} ||^2} \Big )\left\| {f} \right\|^2} \right]||{\tilde {C}} ||^2\notag\\ &\qquad -\Big ( {\sigma _2 -\frac{1}{2\eta }-\frac{1}{2}\Gamma \phi _M^2 || {BR^{-1}B^{\rm T}} ||^2}-\notag\\ &\qquad {\frac{1}{\mu }\Sigma || {\Xi \nabla \varepsilon _1 \frac{1}{2}BR^{-1}B^{\rm T}\nabla \Phi ^{\rm T}} ||^2}\Big)|| {\tilde {W}} ||^2 -\notag\\ &\qquad \Big [{{ K}\lambda _{\min } (Q)-\Gamma \Big ( {4+2\left\| A \right\|+|| {\hat {C}} ||^2\kappa ^2} \Big )}-\notag\\ &\qquad {\frac{1}{\mu }\Sigma \Big ( {|| {\Xi \nabla \varepsilon _1 \hat {C}^{\rm T}} ||^2\kappa ^2}{+\left\| {\Xi \nabla \varepsilon _1 A} \right\|^2} \Big)} \Big]\left\| e \right\|^2-\notag\\ &\qquad \left( {{ K}\lambda _{\min } (R)-\Gamma \left\| B \right\|^2} \right)\left\| {u_e^\ast } \right\|^2-\Big[\Sigma (2\ell -5\mu )-\frac{\eta}{2}\Big]\left\| {\psi _2 } \right\|^2 +\notag\\ &\qquad \frac{1}{2}\Gamma \left\| {BR^{-1}B^{\rm T}} \right\|\left( {\nabla \varepsilon _1 } \right)^{\rm T}\nabla \varepsilon _1 +\Gamma \varepsilon ^{\rm T} \varepsilon +\Gamma \varepsilon _\varphi ^{\rm T} \varepsilon _\varphi +\frac{1}{2}\eta \varepsilon _{1\psi }^2 +\notag\\ &\qquad \frac{1}{\mu }\Sigma \left\| {\Xi (W^{\ast {\rm T}}\nabla \Phi +\nabla \varepsilon _1 )\left( {\varepsilon _\varphi +\varepsilon } \right))} \right\|^2+\notag\\ &\qquad \frac{1}{\mu }\Sigma || {\Xi \nabla \varepsilon _1 \frac{1}{2}BR^{-1}B^{\rm T}\nabla \Phi ^{\rm T}W^\ast } ||^2. \end{align} | (A6) |
The design parameters $\eta $,$\mu $,$\Gamma $,$\Sigma $ and ${K}$ are appropriately chosen such that $\left( {{K}\lambda _{\min } (R)-\Gamma \left\| B \right\|^2} \right)>0$ and the scalars $a_1 $,$a_2 $,$a_3 $ and $a_4 $ are positive and larger than certain positive constant $a>0$,where \begin{align} \nonumber \begin{split} a_1 &= {\sigma _1 -\frac{1}{2\eta }-\left( {\Gamma +\frac{1}{\mu }\Sigma \left\| {\Xi (W^{\ast {\rm T}}\nabla \Phi +\nabla \varepsilon _1 )} \right\|^2} \right)\left\| {f} \right\|^2},\\ a_2 &=\sigma _2 -\frac{1}{2\eta }-\frac{1}{2}\Gamma \phi _M^2 \left\| {BR^{-1}B^{\rm T}} \right\|^2-\\ &\frac{1}{\mu }\Sigma || {\Xi \nabla \varepsilon _1 \frac{1}{2}BR^{-1}B^{\rm T}\nabla \Phi ^{\rm T}} ||^2 ,\\ a_3 &= { K}\lambda _{\min } (Q)-\Gamma \left( {4+2\left\| A \right\|+|| {\hat {C}} ||^2\kappa ^2} \right)-\\ &{\frac{1}{\mu }\Sigma \left( {|| {\Xi \nabla \varepsilon _1 \hat {C}^{\rm T}} ||^2\kappa ^2+\left\| {\Xi \nabla \varepsilon _1 A} \right\|^2} \right)} ,\\ a_4 &=\Sigma (2\ell -5\mu )-\frac{\eta}{2}. \end{split} \end{align} This can be achieved by selecting $\eta >0$ and ${ K}>0$ large enough,while $a>0$,$\mu >0$,$\Gamma >0$ and $\Sigma >0$ are chosen to be small enough to satisfy in particular $\min (\sigma _1 ,\sigma _2 )>a>0$ and $a_4 >a>0$. Note also that Lipschitz continuity of $f(\cdot )$ and smoothness of $\Phi (\cdot )$ and $V^\ast (\cdot )$ imply that $f(\cdot )$,$\Xi $ and $\Phi (\cdot )$ are bounded on $\tilde {\Omega }$. Thus,(A6) can be further presented as
| \begin{align} \label{eq51} \dot {V}\le -a_1 || {\tilde {C}} ||^2-a_2 || {\tilde {W}} ||^2-a_3 \left\| e \right\|^2-a_4 \left\| {\psi _2 } \right\|^2+\gamma, \end{align} | (A7) |
1) In case that there are no approximation errors in both identifier and critic NN,i.e.,$\varepsilon _N \mbox{=}\nabla \varepsilon _1 =\psi _{1} =\psi _{2} =\varepsilon _\varphi =0$, then we have $\gamma =0$,such that (A7) can be deduced as
| \begin{align} \label{eq52} \dot {V}\le -a_1 || {\tilde {C}} ||^2-a_2 || {\tilde {W}} ||^2-a_3 \left\| e \right\|^2-a_4 \left\| {\psi _2 } \right\|^2\le 0. \end{align} | (A8) |
In this case,by assuming the critic NN approximation error $\nabla \varepsilon _1 =0$,we have
| \begin{align} %\label{eq53}\begin{split} \hat {u}_e -u_e^\ast &=-\frac{1}{2}R^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\hat {W}+\frac{1}{2}R^{-1}B^{\rm T}\nabla \Phi ^{\rm T}W^\ast =\notag\\ &\frac{1}{2}R^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\tilde {W}, %\end{split} \end{align} | (A9) |
| \begin{align} \label{eq54} \mathop {\lim }\limits_{t\to +\infty } \left\| {\hat {u}_e -u_e^\ast } \right\|\le \frac{1}{2}\phi _M || {R^{-1}B^{\rm T}} ||\mathop {\lim }\limits_{t\to +\infty } || {\tilde {W}} ||=0. \end{align} | (A10) |
2) In case that there are bounded approximation errors in both identifier and critic NN,then we have $\gamma \ne \mbox{0}$. Consequently,according to (A7),it can be shown that $\dot {V}$ is negative if
| \begin{align} %\begin{split} \label{eq55} &|| {\tilde {C}} ||>{\sqrt {\gamma /a_1 }} ,{\begin{array}{*{20}c} \hfill & \hfill \\ \end{array} }|| {\tilde {W}} ||>{\sqrt {\gamma /a_2 }} ,{\begin{array}{*{20}c} \hfill & \hfill \\ \end{array} }\notag\\ &\left\| e \right\|>{\sqrt {\gamma /a_3}} ,{\begin{array}{*{20}c} \hfill & \hfill \\ \end{array} }\left\| {\psi _2 } \right\|>{\sqrt {\gamma /a_4}} . %\end{split} \end{align} | (A11) |
Next we will prove $\left\| {\hat {u}_e -u_e^\ast } \right\|\le \varepsilon _u $. Recalling the expressions of $u_e^\ast $ from (24) or (30) and $\hat {u}_e $ from (28),we have
| \begin{align} & \hat {u}_e -u_e^\ast =-\frac{1}{2}R^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\hat {W}+\frac{1}{2}R^{-1}B^{\rm T}(\nabla \Phi ^{\rm T}W^\ast +\nabla \varepsilon _1 ) \notag\\ &\qquad \quad =\frac{1}{2}R^{-1}B^{\rm T}\nabla \Phi ^{\rm T}\tilde {W}+\frac{1}{2}R^{-1}B^{\rm T}\nabla \varepsilon _1. \end{align} | (A12) |
| \begin{align} &\left\| {\hat {u}_e -u_e^\ast } \right\|\le \frac{1}{2}|| {R^{-1}B^{\rm T}\nabla \Phi ^{\rm T}} |||| {\tilde {W}} ||+\notag\\ &\qquad \frac{1}{2}|| {R^{-1}B^{\rm T}} ||\left\| {\nabla \varepsilon _1 } \right\|\le \varepsilon _u. \end{align} | (A13) |
Clearly,the upper bound $\varepsilon _u $ depends on the critic NN approximation error $\tilde {W}$ and the NN estimation error $\nabla \varepsilon _1 $.
| [1] | Lewis F L, Vrabie D, Syrmos V L. Optimal Control. Wiley.com, 2012. |
| [2] | Vrabie D, Lewis F L. Neural network approach to continuous-time directadaptive optimal control for partially unknown nonlinear systems. NeuralNetworks, 2009, 22(3): 237-246 |
| [3] | Sastry S, Bodson M. Adaptive Control: Stability, Convergence, andRobustness. New Jersey: Prentice Hall, 1989. |
| [4] | Ioannou P A, Sun J. Robust Adaptive Control. New Jersey: PrenticeHall, 1996. |
| [5] | Sutton R S, Barto A G. Reinforcement Learning: An Introduction.Cambridge: Cambridge University Press, 1998. |
| [6] | Doya K J. Reinforcement learning in continuous time and space. Neuralcomputation, 2000, 12(1): 219-245 |
| [7] | Sutton R S, Barto A G, Williams R J. Reinforcement learning is directadaptive optimal control. IEEE Control Systems Magazine, 1992, 12(2):19-22 |
| [8] | Werbos P J. A menu of designs for reinforcement learning over time.Neural Networks for Control. MA, USA: MIT Press Cambridge, 1990.67-95 |
| [9] | Si J, Barto A G, Powell W B, Wunsch D C. Handbook of Learning andApproximate Dynamic Programming. Los Alamitos: IEEE Press, 2004. |
| [10] | Wang F Y, Zhang H G, Liu D R. Adaptive dynamic programming:an introduction. IEEE Computational Intelligence Magazine, 2009, 4(2):39-47 |
| [11] | Lewis F L, Vrabie D. Reinforcement learning and adaptive dynamic programmingfor feedback control. IEEE Circuits and Systems Magazine,2009 9(3): 32-50 |
| [12] | Zhang H G, Zhang X, Luo Y H, Yang J. An overview of research onadaptive dynamic programming. Acata Automatica Sinica, 2013, 39(4):303-311 |
| [13] | Dierks T, Thumati B T, Jagannathan S. Optimal control of unknownaffine nonlinear discrete-time systems using offline-trained neural networkswith proof of convergence. Neural Networks, 2009, 22(5):851-860 |
| [14] | Al-Tamimi A, Lewis F L, Abu-Khalaf M. Discrete-time nonlinearHJB solution using approximate dynamic programming: convergenceproof. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics, 2008, 38(4): 943-949 |
| [15] | Wang D, Liu D R, Wei Q L, Zhao D B, Jin N. Optimal control ofunknown nonaffine nonlinear discrete-time systems based on adaptivedynamic programming. Automatica, 2012, 48(8): 1825-1832 |
| [16] | Hanselmann T, Noakes L, Zaknich A. Continuous-time adaptive critics.IEEE Transactions on Neural Networks, 2007, 18(3): 631-647 |
| [17] | Abu-Khalaf M, Lewis F L. Nearly optimal control laws for nonlinearsystems with saturating actuators using a neural network HJB approach.Automatica, 2005, 41(5): 779-791 |
| [18] | Vrabie D, Pastravanu O, Abu-Khalaf M, Lewis F L. Adaptive optimalcontrol for continuous-time linear systems based on policy iteration.Automatica, 2009, 45(2): 477-484 |
| [19] | Vamvoudakis K G, Lewis F L. Online actor-critic algorithm to solve thecontinuous-time infinite horizon optimal control problem. Automatica,2010, 46(5): 878-888 |
| [20] | Bhasin S, Kamalapurkar R, Johnson M, Vamvoudakis K G, Lewis F L,Dixon W E. A novel actor-critic-identifier architecture for approximateoptimal control of uncertain nonlinear systems. Automatica, 2013, 49(1):82-92 |
| [21] | Zhang H G, Cui L, Zhang X, Luo Y. Data-driven robust approximateoptimal tracking control for unknown general nonlinear systems usingadaptive dynamic programming method. IEEE Transactions on NeuralNetworks, 2011, 22(12): 2226-2236 |
| [22] | Mannava A, Balakrishnan S N, Tang L, Landers R G. Optimal trackingcontrol of motion systems. IEEE Transactions on Control SystemsTechnology, 2012, 20(6): 1548-1558 |
| [23] | Nodland D, Zargarzadeh H, Jagannathan S. Neural network-basedoptimal adaptive output feedback control of a helicopter UAV. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(7):1061-1073 |
| [24] | Na J, Herrmann G, Ren X M, Mahyuddin M N, Barber P. Robust adaptivefinite-time parameter estimation and control of nonlinear systems. In: Proceedings of IEEE International Symposium on Intelligent Control(ISIC). Denver, CO: IEEE, 2011.1014-1019 |
| [25] | Uang H J, Chen B S. Robust adaptive optimal tracking design foruncertain missile systems: a fuzzy approach. Fuzzy Sets and Systems,2002, 126(1): 63-87 |
| [26] | Krstic M, Kokotovic P V, Kanellakopoulos I. Nonlinear and AdaptiveControl Design. New York: Wiley, 1995. |
| [27] | Kosmatopoulos E B, Polycarpou M M, Christodoulou M A, Ioannou PA. High-order neural network structures for identification of dynamicalsystems. IEEE Transactions on Neural Networks, 1995, 6(2): 422-431 |
| [28] | Abdollahi F, Talebi H A, Patel R V. A stable neural network-based observerwith application to flexible-joint manipulators. IEEE Transactionson Neural Networks, 2006, 17(1): 118-129 |
| [29] | Lin J S, Kanellakopoulos I. Nonlinearities enhance parameter convergencein strict feedback systems. IEEE Transactions on AutomaticControl, 1999, 44(1): 89-94 |
| [30] | Edwards C, Spurgeon S K. Sliding Mode Control: Theory and Applications.Boca Raton: CRC Press, 1998. |
| [31] | Sira-Ramirez H. Differential geometric methods in variable-structurecontrol. International Journal of Control, 1988, 48 (4): 1359-1390 |
| [32] | Nevistic V, Primbs J A.Constrained Nonlinear Optimal Control: AConverse HJB Approach, Technical Report CIT-CDS 96-021. California Institute of Technology, Pasadena, CA, 1996. |
 2014, Vol.1
2014, Vol.1 


