2. Assistant Professor, Department of Systems and Industrial Engineering, Department of Aerospace and Mechanical Engineering, University of Arizona, 1127 E. James E. Rogers Way, Tucson, AZ 85721, USA
FUTURE unconstrained,science-driven,robotic and human missions to Mars will require a higher degree of landing accuracy. Indeed,the next generation of Mars landers will require more advanced guidance and control capabilities to satisfy the increasingly stringent accuracy requirements driven by the desire to explore Mars regions that have the potential to yield the highest scientific return. The Mars Science Laboratory (MSL)[1],which landed on Mars during the summer of 2012,is a clear example of a mission where the scientific desire to explore regions that have never been previously accessed before required the development and implementation of a novel guidance approach that can deliver the mobility system on the Martian surface with higher precision than previous attempts. For the earlier phoenix Mars lander[2],the entry,descent and landing (EDL) mission profile included two unguided phases followed by a powered descent segment designed to close the loop only on the altitude while attempting to reduce the velocity to zero. As a result,the landing error ellipse was estimated to be of the order of 120 km[2]. The MSL lander was expected to reduce the landing error to less than 10 km,which has been achieved by implementing an active bank angle control during the hypersonic entry phase[1]. Moreover,according to the EDL timeline,after the MSL unguided parachute deceleration phase is completed,a powered descent 5th order polynomial trajectory is computed onboard to implement a linear,closed-loop, trajectory-following approach that the spacecraft executes to safely land on the surface within the predicted error ellipse[3]. Importantly,the powered descent phase guidance algorithm does not have the ability to select the desired location within the landing ellipse,i.e. the selected landing point on the surface is designed to be located at a pre-fixed downrange and crossrange distance from the point where the liquid rockets are activated. Although a 10 km landing precision has never been achieved on Mars,this accuracy is still far from the precision required by upcoming missions.
Future missions to Mars may also require the ability to execute real-time retargeting while en-route toward the planet$'$s surface. Such maneuvers may be necessary to avoid obstacles that would interfere with the safety of the spacecraft during landing. Since such obstacles may not be apparent when the landing site is initially selected,it is important that during the powered descent segmentthe lander autonomously identifies hazardous landing sites and dynamically retargets itself to a safer site. In practice andwithin the lander$'$s retargeting capabilities,a pattern recognition algorithm coupled with some combination of radar and optical inputs could be employed to determine a target site that provides the highest probability of a safe landing. The estimate of the best landing site would be continuously updated until the safe landing is achieved.
To date,most of the powered descent algorithms for planetary landing have been based on variations of the Apollo guidance algorithm[4]. The original guidance approach,which was used to drive the lunar exploration module (LEM) to the lunar surface, was based on an iterative approach that computed offline a flyable reference trajectory in the form of a quartic polynomial[5]. The real-time guidance algorithm would subsequently generate an acceleration command that tracks the pre-computed reference trajectory. While effective for past missions,such class of guidance algorithms may not be able to satisfy more stringent landing requirements imposed by novel mission architectures designed for precision landing.
Over the past few years,nonlinear and adaptive control theory made significant progress in developing algorithms that improve robustness against perturbations and un-modeled dynamics. Guidance algorithms for planetary landing and retargeting employing nonlinear methodologies such as Lyapunov second method[6] and sliding model control[7] have been recently proposed. Importantly, adaptive control theory has promised to improve systems performance by adapting the control law to unknown system parameters and uncertain environments. As part of adaptive methods,neural networks[8] represent an interesting class of intelligent and adaptive algorithms that have the ability to learn the un-modeled dynamics either indirectly (i.e.,offline) or directly (i.e., online). Conventional multi-layer perceptrons (MLP) trained on back propagation have already been employed to develop adaptive controllers for endoatmospheric flight systems[9]. Recently, reinforcement learning (RL) theory,where the dynamical system to be guided/controlled is treated as a Markov decision process (MDP)[10],has been employed to develop controllers that can be trained to learn optimal control policies[11, 12].
In this paper,RL theory is applied to the problem of Mars landing to show how an adaptive,RL-based guidance algorithm can be trained to autonomously learn the best landing policy,i.e. the sequence of acceleration/thrust commands that yields trajectories that are fuel-efficient yet accurate in terms of desired final position and velocity (soft landing). The landing problem is cast as an MDP and a neural network guidance algorithm is developed. The learning procedure consists of finding the network$'$s weights that maximize the expected utility. The latter ensures that only control policies that drive the lander to the desired location with maximum accuracy and minimum fuel consumption are selected. Importantly,the proposed strategy does not require any reference trajectory but,during the course of the training,the network learns to autonomously land optimally using current position and velocity information as provided by the navigation system. Moreover,the system can learn a policy that is optimal in the presence of adverse effects such as environmental noise,sensor and actuator noise,and sensor and actuator delays.
The paper is organized as follows. In Section II,the theory behind MDP and RL is briefly introduced. In Section III,the guidance problem is formulated as a Markov decision process. Subsequently,the approach employed to determine the RL-based landing guidance algorithm is described. Apprentice learning is employed to initialize the neural network weights designed to approximate the continuous map between lander states (position and velocity) and actions (thrust command). This is followed by running a stochastic search algorithm to determine the optimal landing policy under environmental uncertainties and un-modeled dynamics. In Section IV,the results obtained from apprenticeship learning and stochastic optimization are reported together with a set of Monte Carlo simulations executed to evaluate the performance of the RL-based landing guidance algorithm. The RL-based guidance algorithm is compared to an Apollo-like guidance scheme. Section V draws conclusions and suggests future work.
Ⅱ. MARKOV DECISION PROCESS AND REINFORCEMENT LEARNINGRL is a machine learning technique concerned with how an agent (e.g.,lander) must take actions in uncertain environments to maximize a cumulative reward (i.e.,minimize the landing errors). The stochastic environment is conventionally formulated as an MDP where the transition between states for a given action are modeled using an appropriate state transition probability distribution. An MDP consists of a) a set of states $S$ (where ${\pmb s}$ denotes a state ${{\pmb s}}\in S)$,b) a set of actions $A$ (where ${\pmb a}$ denotes an action ${{\pmb a}}\in A)$,c) a reward function $R({{\pmb s}})\mapsto R $ that maps a state (or possibly a state-action pair) to the set of real numbers,d) state transition probabilities $P_{sa} $,which defines the probability distribution over the new state ${{\pmb {s}'}}\in S$ that will be transitioned when a given action ${\pmb a}$ is taken while in state ${\pmb s}$,and ${e}$) an optional discount rate $\gamma $ that is typically used for infinite horizon problem
RL algorithms learn a policy $\pi ({{\pmb s}}): S\mapsto A$ that maps each state to an optimal action. For a given trajectory, these actions are considered optimal if they maximize the policy$'$s utility over that trajectory. The utility is defined as the expected value of the sum of discounted rewards that results from starting in state ${\rm s}_0 $and following the policy $\pi $. For a single trajectory $i$,one can write the following:
| $ \begin{align} %General Multi-Layer Neural Network Architecture} U^{(i)}(\pi )={\rm E}\left[{R({{\pmb s}}_0 ^{(i)})+\gamma R({{\pmb s}}_1 ^{(i)})+\gamma ^2R({{\pmb s}}_2 ^{(i)})+\cdots } \right]. \end{align} $ | (1) |
Here,the expectation accounts for the stochastic nature of the environment,whereas the sequence ${{\pmb s}}_0^{(i)},{{\pmb s}}_1 ^{(i)},{{\pmb s}}_2 ^{(i)},\cdots $ defines the trajectory associated with starting from initial condition $i$ and following policy $\pi $.
In general,many controlled dynamical systems consist of an infinite number of possible trajectories. For example,consider the problem of simultaneously stabilizing an inverted pendulum attached to a cart on a bounded track and maintaining the cart$'$s position at some desired location. In this case,the MDP state vector is the concatenation of the cart$'$s position and velocity andthe pendulum$'$s angle and angular velocity (i.e.,$[x,\dot {x},\theta ,\dot {\theta }]^{\rm T})$,and the MDP action (a scalar) is the acceleration imparted to the cart. For any possible initial state, it is desired to generate a sequence of acceleration commands that drives the system state to the desired final state,which for this problem is $[x_f ,0,\theta _f ,0]^{\rm T}$. In this example,any possible initial state will define a unique trajectory --- possibly over an infinite horizon,unless the controller finds a steady state control that keeps the pendulum balanced. For this type of problem,one can estimate a policy$'$s utility using a sampling approach. In such a case,the estimate would be calculated as either the average or minimum utility over the sample trajectories:
| $ \begin{align} U(\pi )=\frac{1}{N}\sum\limits_{i=1}^N {U^{(i)}(\pi )} \mbox{ or }U(\pi )=\mathop {\min }\limits_i U^{(i)}(\pi ). \end{align} $ | (2) |
Many RL-based algorithms approach the problem of determining the optimal policy indirectly,i.e.,through the value function. For a given policy $\pi $,the value function is defined as the expected sum of rewards given that the system is in state s and executes policy $\pi $. The value function can be expressed as the sum of the reward associated with being in the current state and the value of the discounted expectation over the distribution of next states given that the controller is following policy $\pi $:
| $ \begin{align} V^\pi ({\pmb s})=R({\pmb s})+\gamma \sum\limits_{{\pmb s}'}\in S {P_{s \pi (s)} } ({{{\pmb s}'}})V^\pi ({{{\pmb s}'}}) \end{align} $ | (3) |
The optimal value function,$V^\ast ({{\pmb s}})$ is generally found using dynamic programming algorithms,e.g.,value iteration[10, 13]. Once the optimal value function is determined,the optimal policy is determined by taking the action that maximizes the expected sum of future rewards for the given current state; using (3),the optimal policy can be formally expressed as follows:
| $ \begin{align} \pi ^\ast ({{\pmb s}})=\arg \mathop {\max }\limits_{{{\pmb a}}\in A} \sum\limits_{{{\pmb {s}'}}\in S} {P_{\pmb sa} } ({{\pmb {s}'}})V^\ast ({{\pmb {s}'}}). \end{align} $ | (4) |
The principal limitation of this approach is that both the state and action space must be discretized. As a result,the number of discrete states and actions grow exponentially with the dimensionality of the state and action spaces. Often the state space has higher dimensionality than the action space; consequently it is often easier to discretize the action space than the state space. When this is the case,fitted value iteration[13, 14],which learns a model that represents the value function as a continuous function of the state,may be effectively employed to determine the optimal policy. Suitable value approximation functions for fitted value iteration include least squares,weighted least squares,and neural networks using online learning. If it is necessary to work with continuous state and action spaces --- as is the case where the action space has high dimensionality,one approach (direct policy optimization[15]) is to dispense with the value function,and directly search for the optimal policy.
A. Relationship Between RL and Conventional Optimal ControlNote that the concepts used to define the reinforcement learning problem have a clear counterpart to those used to define the optimal control problem: the policy becomes the controller,the action becomes the control,the state transition probabilities becomes the plant,the utility becomes the negative cost,whereas the state remains the state. Unfortunately,there is one significant limitation that is inherent to the optimal control framework,i.e.,the system must be modeled as a system of deterministic differential equations. However,there are many examples of physical systems (e.g.,helicopter dynamics,airframe dynamics in turbulent airflow) that are of sufficient complexity that they are most accurately modeled stochastically. Consequently,such system may be best optimized using a framework that can accommodate stochastic models.
Conversely,with RL,the system model need not be mathematical,but can instead be a statistical model learned from test flight telemetry and wind tunnel data using machine learning techniques, e.g.,weighted linear regression[13],neural networks[8], mixtures of Gaussians[16],and probabilistic graphical models[17]. For complex dynamical systems,these stochastic models can be expected to be more accurate than a simplified mathematical model.
Ⅲ. GUIDANCE LAW DEVELOPMENT A. Problem Formulation: MDP State,Action,Reward and State Transition Probability DistributionThe overall goal is to develop a novel RL-based guidance algorithm capable of autonomously landing on planetary bodies in general,and Mars in particular. Following the generic approach to RL design as described in the previous section requires a proper definition of the state space,action space,reward function,andthe state transition probability distribution. For the landing guidance,the state is defined by the vector ${{\pmb s}}=[x,y,z,\dot {x},\dot {y},\dot {z}]^{\rm T}$,where $x$ represents the lander$'$s downrange position,$y$ the lander$'$s crossrange position,and $z$ the lander$'$s altitude,all with respect to the target site; the action is defined by the lander$'$s thrust vector ${\rm {\pmb a}}=[T_x ,T_y ,T_z]$; the reward is function of the error in position and velocity at the terminal (absorbing) state as well as the difference between initial and final spacecraft mass. In general,the reward function is chosen to be quadratic in the lander$'$s relative position and velocity,and linear in the change in the lander$'$s mass. The choice of the reward function is motivated by the fact that during the learning process the system is rewarded if the guidance algorithm chooses trajectories that tend to maximize the reward,i.e.,trajectories that minimize the fuel consumption yet provide low residual guidance error (position and velocity).
Assuming that the target state is located at the origin of the coordinate frame (i.e. zero position and velocity),the reward function is consequently defined as follows:
| $ \begin{align} R({{\pmb s}}={{\pmb s}}_{{f}} )=-\alpha \left\| {[x,y,z]} \right\|^2-\beta \left\| {[\dot {x},\dot {y},\dot {z}]} \right\|^2-\delta (m_i -m_f ). \end{align} $ | (5) |
Here,${{\pmb s}}_f $ is the final absorbing state,$m_i $ and $m_f$ are the spacecraft$'$s mass at the start and end of the landing trajectory,and $x$,$y$,and $z$ are the downrange, crossrange,and elevation position components at the end of the trajectory. The coefficients are used to keep the size of each term roughly equal toward the end of the trajectory.
To complete the RL framework,the MDP$'$s state transition probability distribution must be specified,with this distribution modeling the environment. Within the MDP formulation,the environment comprises not only factors like gravity,wind,and variations in atmospheric pressure,but also parts of the lander that are controlled by the policy,including actuators and sensors. Therefore,the state transition probabilities need to include the effects of actuator and sensor noise,as well as actuator delays. For example,the lander might be at some true position and velocity,but the lander$'$s sensors will convey this true state to the controller with the addition of Gaussian noise.
The environmental dynamics for the powered descent guidance towards Mars$'$ surface,which describes the transition probabilities of the underlying MDP,is modeled using a stochastic 3-DOF model with variable mass and constant gravitational field. It is assumed that the landing site is centered on the origin of coordinate system specified in rectangular coordinates. In vector form,the equations of motion are:
| $ \begin{align} & { {\pmb v}}={ \dot{\pmb {r}}} \notag\\ & { \dot{\pmb {v}}}=\frac{{ {\pmb T}}}{m}+\left[{0,0,-g} \right]^{\rm T}+\frac{{ {\pmb F}}_{ENV} }{m},\notag\\ & \dot {m}=-\frac{\left\| { {\pmb T}} \right\|}{g_{ref} I_{sp} }, \end{align} $ | (6) |
here $g_{ref} =9.8 \mbox{m/s}^2$ is the reference gravity, $g=3.7114 \mbox{m/s}^2$ is the Martian gravity,$I_{sp} =225 {\rm s}$ is the lander specific impulse,and $m$ is spacecraft mass. ${{\pmb F}}_{ENV} $ is a vector of normally distributed random variables representing environmental disturbances such as wind,variations in atmospheric density,and any other un-modeled forces acting on the lander. The engine$'$s perturbed specific impulse,$I_{sp} $,is also assumed to be a normally distributed random variable,with the randomness accounting for un-modeled engine dynamics. Importantly,for this study,the effects of atmospheric drag and planetary rotation are ignored.
Sensor noise is modeled by adding Gaussian noise to each of the state variables before they are input to the RL-based controller that implements the policy. Each state variable is corrupted as follows:
| $ \begin{align} s_i =s_i +\left| {s_i } \right|{\rm N}(0,\sigma _{SN} ),\quad i=1,2,3,4,5,6, \end{align} $ | (7) |
here $\sigma _{SN} $ is the standard deviation of the sensor noise. Note that sensor noise only affects the policy$'$s estimate of the lander current state,as opposed to perturbing the actual state.
Environmental noise,which models the effect of wind and variation in atmospheric density,perturbs the current state as given by the equations of motion. The perturbation is modeled as a force vector acting on the spacecraft that is normally distributed with mean $\vec {\mu }_{EN} $ and standard deviation $\vec {\sigma }_{EN} $:
| $ \begin{align} {{\pmb F}}_{ENV} ={\rm N}(\vec {\mu }_{ENV} ,\vec {\sigma }_{ENV} ). \end{align} $ | (8) |
As a rough estimate of the force caused by wind gusts,a cross sectional lander area of 100 square feet was assumed. The Cornell University Earth wind pressure calculator[18] was employed to compute the resulting wind pressure in pounds per square foot. The outcome was divided by 168 to account for the difference in average surface air pressure between the Earth and Mars and multiplied by the assumed cross section of the lander before converting to Newtons. According to the proposed approximation,a wind of 100 m/s would result in a force of 162 N,which is fairly close to the standard deviation of the environmental disturbance used in Case 3 in Table Ⅰ. Note that the Mars GRAM model[19] shows a strong jet near 5-km altitude and 70 degrees N latitude with winds reaching 100 m/s,so it is reasonable to expect a Lander to be able to handle this case as a worst-case scenario.
|
|
Table Ⅰ INITIAL CONDITIONS |
The actuator delay is modeled as a single time constant autopilot delay,with the actual thrust ${{\pmb T}}$ being a function of the thrust command given by the policy ${{\pmb T}}_{{C}}$ and the actuator time constant $\tau $:
| $ \begin{align} \tau \frac{{\rm d}{\pmb T}}{{\rm d}t}+{ {\pmb T}} = {\pmb T}_{C}. \end{align} $ | (9) |
Actuator noise is modeled as a perturbation in the engine$'$s mass flow rate variation,where the engine$'$s perturbed specific impulse $I_{sp} $ is given in terms of a nominal value $I_{nsp} $ and the standard deviation of the mass flow rate variation $\sigma _{AN} $:
| $ \begin{align} I_{sp} =I_{nsp}+I_{nsp}{\rm N}(0,\sigma _{AN}). \end{align} $ | (10) |
Once the landing guidance problem is formulated as an MDP,the next step is to determine the policy that is optimal with respect to accuracy and fuel-efficiency. In the RL framework,the policy is determined via simulated experience,where the agent (controller) learns the optimal actions that will drive the lander to the desired position with minimum fuel. In general terms,an optimal landing policy generates optimal actions for a given state. Here,the action is defined as optimal in that it leads to reaching the intended landing site with close to zero velocity through a closed-loop trajectory that is fuel-efficient over a wide range of initial conditions. Clearly,the optimal policy must have the ability to map the lander$'$s current state into a specific action that generates closed-loop trajectories with the desired above mentioned properties. And since the action space is three dimensional,it is on the boundary of efficient discretization,which implies the need for algorithms capable of describing continuous state-action maps, i.e.,direct policy optimization. Neural Network algorithms have the ability to describe continuous input-output functions using a finite numbers of free parameters (weights). Importantly,the number of weights,which is directly related to the number of neurons comprising the network architecture,depends on the complexity of the modeled functional relationship between state and action.
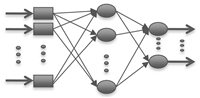
For the Mars landing guidance problem,the policy is implemented using a multi-layer neural network[8]. Fig. 1 illustrates the general architecture of a neural network with some arbitrary number of inputs (denoted by rectangles),nodes (denoted by ovals),and outputs. The designed network comprises one input layer (current lander state vector),one hidden layer and one output layer (the action vector). Here,the internal connections are assumed to have an associated weight. Importantly,each node implements a summation of the incoming weighted signals and applies some activation function to the result of the summation. In this application,a hyperbolic tangent activation function is used for hidden neurons,and a linear activation function for output neurons. More specifically,the output of hidden layer node $j$ is given by the following:
| $ \begin{align} a_j =\tanh \left( {\sum\limits_{i=1}^{n {\rm inputs}} {w_{ij} } } \right),\end{align} $ | (11) |
where $w_{ij} $ denotes the weight connecting input $i$ to hidden layer node $j$. For the linear layer,the output of hidden layer node $k$ is given by the following:
| $ \begin{align}a_k =\sum\limits_{j=1}^{n {\rm hidden}} {w_{jk} }, \end{align} $ | (12) |
where $w_{jk}$ denotes the weight connecting hidden layer node $j$ to output layer node $k$. Note that the input layer and hidden layer are both augmented with a bias node (not shown) with an associated weight from that node to each node in the next layer.
|
Download:
|
| Fig. 1. General multi-layer neural network architecture. | |
Once the network architecture is defined,the next step is to optimize the policy via a set of simulated experiences that are generated using the MDP model. Policy optimization requires weight initialization followed by an iterative process that adjusts the network weights until the utility is maximized. Although in theory it is possible to learn an optimal policy with no prior knowledge, i.e.,by initializing the network with random weights,the learning process can be dramatically accelerated if the learning is initiated using known open-loop optimal trajectories. Such a technique is known as apprenticeship learning[20]. Sometimes called learning by watching,imitation learning or learning from demonstration,apprentice learning can be defined as the process of estimating the policy of an expert from samples of the expert$'$s behavior. In our case,the apprentice learning technique is implemented by computing the policy for specified number of open-loop fuel-efficient landing trajectories that drive the spacecraft to the desired location with zero velocity. Such trajectories and the guidance required to drive the spacecraft to the desired location are the samples employed to approximate the optimal policy of the expert. Once such samples are determined, the neural network can be trained using conventional learning techniques to determine the weights that approximate the desired policy. Once the training process is completed and validated,the resulting weights are taken to be the initial set of parameters that seeds the RL process. The overall goal is to use approximate expert knowledge to accelerate the convergence of the RL to the desired optimal policy.
Open-loop optimal trajectories can be generated off-line using appropriate numerical methods. Pseudo-spectral methods have been shown to be fast and reliable in solving a wide variety of optimal problems[21, 22, 23, 24, 25, 26, 27, 28, 29, 30]. In this paper,the Gauss pseudospectral optimal control software (GPOPS)[24, 31] is used to generate off-line a set of open-loop fuel-efficient trajectories. Examples of such optimal trajectories are reported in Fig. 2. Details of the optimal trajectory generation for Mars landing are reported in Appendix A.

|
Download:
|
| Fig. 2. Sample optimal trajectories (left panel) and the vector velocity field (right panel) as computed using GPOPS. | |
The fuel-efficient trajectories can be represented as a time series of state vectors and associated thrust (control) vectors. If $m$ samples are available from optimal trajectories[21] one can create a design matrix ${{X}}\in R ^{m \times 6}$, each row containing a sampled state vector ${{\pmb s}}=\left[ {{\begin{array}{*{20}c} x & y & z & {\dot {x}} & {\dot {y}} & {\dot {z}} \\ \end{array} }} \right]$,and a target matrix ${{\pmb Y}}\in R ^{m \times 6}$,each row containing an associated sampled optimal action vector ${{\pmb a}}=\left[{{\begin{array}{*{20}c} {{T}_x } & {{T}_y } & {{T}_z } \\ \end{array} }} \right]$. These matrices represent the input-output pairs that comprise the network training set. Taking care to avoiding overtraining,the goal is to obtain a network capable of generalizing the relationship between the current state and optimal action. Once trained,novel inputs (i.e.,states outside the training set but that are still within the range where the network was trained) can be processed by the network in real-time to obtain a reasonable approximation of the desired optimal action. The network is trained using a modified version of the back-propagation approach that accommodates the Levenberg-Marquardt minimization algorithm. Generalization is achieved via Bayesian regularization[32],which introduces a penalty term into the performance function used for training. The latter has been specifically implemented to make the network less likely to over-fit the data.
D. Policy OptimizationIn principle,apprentice learning may generate a policy that reasonably approximates the optimal policy for precision landing. However,as a stand-alone approach to policy approximation,it is expected to yield rather poor policies. Indeed,during the training process,one implicitly executes a trade-off between achieving accuracy on the training data and implementing good generalization (i.e.,generates good actions in states not in the training set). Such trade-off between training accuracy and generalization ability may result in outliers,i.e.,a set of states not comprised in the training set where the network generates actions that are sub-optimal. The latter may affect the overall performance negatively,precluding fuel efficiency and high accuracy. Moreover,apprenticeship learning using open loop trajectories derived from GPOPS employs design and target matrices that are derived under ideal conditions. Consequently,the resulting policy is expected to be sensitive to noise and un-modeled dynamics,which is not captured by the deterministic model underlying the optimal control problem. To obtain a policy that is optimal with respect to non-idealities such as actuator delays and environmental perturbations,the policy must be optimized in an environment that models these non-idealities, i.e.,to achieve robustness in the presence of noise,the policy must be optimized in a noisy environment. Finally,the trained network may be suboptimal because the cost function used in supervised training has local minima.
Nevertheless,apprenticeship learning is extremely useful in that it obtains an initial setting for the network weights that is expected to speed up the optimization process used in the reinforcement learning approach. Once this initial weight setting is found,one can proceed to further optimize the policy within the MDP framework.
In this application,the policy$'$s utility is estimated as:
| $ \begin{align} U(\pi )=\mathop {\min }\limits_i R(s_f ^{(i)}),\end{align} $ | (13) |
Here the reward function is as defined in (5). The index $i$ indicates a simulated sample from the set of all trajectories realized by following policy $\pi $ from all possible initial states.
Policy optimization involves learning,through simulated experience, which setting of the neural network weights maximizes the utility given by (13). Given some input state,the back propagation method[33] efficiently updates the weights based on the output error (the difference between the actual and target output values). This technique can be extended to back propagate gradient information based on a utility metric[34]. However,because the utility is a function of all actions taken during the powered descent,there is no direct relationship between a given action taken during the descent phase and the utility described in (13). Consequently,estimating the utility gradient requires simulating multiple landing scenarios using the current set of weights. The latter makes the utility gradient evaluation computationally expensive. With this in mind,the policy is optimized using a gradient-free stochastic search algorithm[35]. Not only do these algorithms have the potential for faster convergence,but they are also less prone to get trapped in a local maximum. A similar approach was used by other researchers to solve the autonomous helicopter hovering problem[14].
The algorithm structure is reported in Fig. 3. First,the network weights are set to those determined during the apprenticeship learning phase. Afterward,the policy optimization algorithm is initiated to run a simulation for each set of initial conditions. The initial conditions were chosen using 5 initial positions,4 initial downrange velocities,and 4 initial elevation velocities, all evenly spaced between the minimum and maximum values given in Table Ⅰ (a total of 80 simulations). The baseline utility is then calculated as the minimum utility from each of the 80 simulations using the simulate function. In Fig. 3,the simulate function runs a simulation with the given initial conditions,and returns a scalar value corresponding to the reward function as calculated by (5).

|
Download:
|
| Fig. 3. Policy optimization algorithm. | |
The algorithm then enters the repeat loop. The old set of weightsis saved,and then the weights are perturbed by adding a normally distributed random number with zero mean and a standard deviation equal to the epoch scale factor (the scale variable in Fig. 3). In this application,an initial scale factor of 0.05 is found to be acceptable. The proposed algorithm is expected to converge even with larger initial scale factors. However,when the scale factor gets too large,the weights are completely randomized,and consequently, any information gained through the network pre-training is lost. After the weights are perturbed,a simulation is run for each initial condition in a manner similar to the procedure used to establish the baseline utility. The utility associated with the current set of weights is then calculated and compared against the highest utility found up to that point in the repeat loop (the best$\_$utility variable in Fig. 3). If this utility exceeds the current best utility,then the weights are retained and stored; otherwise the algorithm reverts to the old weights. During the execution of the algorithm,the nimc variable keeps track of the number of loop iterations without any improvement in utility. If nimc exceeds some maximum value (${\rm max\_nimc}$),the scale factor used to perturb the weights is decreased by a factor of 0.9. This implementation used a nimc value of 500. The algorithm is declared to have converged when the variation in utility over the current epoch falls below some threshold. In practice,a Monte Carlo simulation was run at the end of each epoch to establish performance using novel initial conditions,and the algorithm was terminated when the performance became acceptable. Note that although the search is greedy with respect to utility,the fact that the weights are randomly perturbed allows the algorithm to explore regions outside of any potential local minima the algorithm may be trapped in.
Importantly,the density of the initial conditions within the ellipse defining the state dispersion experienced by the spacecraft at the beginning of the powered descent phase is directly related to the density of the samples over the state space. Moreover,the ability of the optimized policy to generate optimal actions for novel states is a function of the sample density over state space. Unfortunately,the authors have not been able to determine a reliable heuristic for determining the required sample density,and consequently the required sampling density was obtained by trial and error.
Unlike most stochastic search algorithms found in the literature, this search algorithm does not make any use of gradient information. This is intentional and consequence of the large number of simulations required toobtain an estimate of the gradient. An alternative approach would have been to estimate the gradient using stochastic methods,as described in [36].
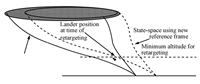
E. Dynamic RetargetingThe proposed RL-based guidance law allows retargeting the landing site during execution of the powered descent phase. Retargeting is accomplished by translating the target centered reference frame to a new origin corresponding to the desired landing site. From the perspective of the policy,the latter results in an instantaneous shift in the lander$'$s position,which is legitimate as long as the shift does not place the lander outside the state-space employed for policy optimization. As shown in Fig. 4,given some distance $d$ between the current target and desired target,there is generally a minimum altitude past which retargeting is infeasible. Note that the minimum allowable altitude decreases with the distance between the original and new reference frame origins.
|
Download:
|
| Fig. 4. Illustration of retargeting constraints. | |
In practice such a constraint should not be an issue because it is likely that the optimal landing site can be determined shortly after the start of the powered descent phase. However,the retargeting process will need to be aware of the lander$'$s position within the post-targeting frame of reference so that the landing site selection function can exclude any landing site that would place the lander outside of the state-space defined by the new reference frame.
Ⅳ. RESULTSIn this section,the optimization results and performance of the RL-based landing guidance algorithm are presented. A 2-DOF model (motion on the vertical plane) has been employed to design and evaluate the algorithm performances. Table Ⅰ shows the bound for downrange,elevation,velocity components and lander mass employed during policy optimization and policy validation. The extension to 3-DOF is conceptually trivial,but requires additional hidden layer nodes in the neural network,and considerably more computational resources Increasing the size and/or the dimensionality of the state space,results in an increase in the required number of hidden layer neurons,which in turn increases the computational resources required for the initial neural network training and the subsequent policy optimization. Alternatively,the problem can be decomposed into two problems in two orthogonal planes. Similarly,the extension to a larger state space requires either a larger number of hidden layers in the neural network or multiple policies assigned to different regions of state space.
In practice the range of initial conditions should represent worst-case bounds for the lander$'$s position once it reaches the nominal altitude of 1 500 m,which triggers the powered descent phase. Since the consequence of the lander finding itself out of the state-space over which the policy was optimized is a loss of control and potential catastrophic impact,it is strongly recommended that sufficient margin be employed during the policy design phase. As the cost of a larger initial condition ellipsoid is merely translated into a more complex neural network (which only impacts optimization time),the cost of higher margin is just larger computational resources (or longer optimization times).
During the powered descent phase,the norm of the lander$'$s thrust vector was constrained to values ranging from 4 972 N to 13 258 N (30 % and 70 % of maximum thrust).
A. Apprenticeship TrainingThe design and target matrices (training set) for the neural network training phase were generated by sampling 847 trajectories generated using GPOPS[31] (see Appendix A),with 21 samples per trajectory. The neural network was designed to have 32 hidden layer nodes. Matlab Neural Network Toolbox® was employed to model the network and execute the training process via the trainbr algorithm (Bayesian regularization). Fig. 5 shows the error histogram after the neural network training phase. Here,the error is the difference between the optimal open-loop action (thrust) and the actual action taken by the network when presented with one of the state vectors comprising the design matrix. As discussed in the previous section,although most of the errors are relatively small,some outliers have considerable error.

|
Download:
|
| Fig. 5. Neural network training Results. For a given input vector in the training set, the error is the difference between the neural network$'$s output (thrust in Newtons) and the corresponding output vector in the training set. | |
To establish a pre-optimization baseline,the trained neural network was simulated for 1 000 different initial conditions randomly selected from the range of initial conditions given in Table Ⅰ. The initial downrange distance was split into 5 evenly spaced samples. Similarly,the initial downrange velocity and initial elevation velocity were split into 4 evenly spaced samples,for a total of 80 initial conditions. As discussed above, the apprentice-based training of the network using open-loop optimal samples is not expected to perform well in every single case. Indeed,as reported in Fig. 1,the network$'$s actual output (thrust) differed by approximately 3 000N from the thrust given in the output matrix for a given input vector in the training set. This resulted in a worst-case landing error distance in the downrange direction at touchdown of $-$218 m,and a worst-case impact velocity at touchdown of 114 m/s in the downrange direction and $-$108 m/s in the vertical direction. For a pinpoint soft landing,the policy is clearly not acceptable. Nevertheless,the trained network serves as a starting point for the MPD-based optimal policy.
B. Policy OptimizationThe optimization was performed in a noisy environment,i.e.,with sensor,actuator,or environmental noise,and actuator delay,as shown in Table Ⅱ. Unlike Ng et al.[12],although the initial conditions were kept deterministic,the algorithm did not pre-compute the random samples used for noise modeling. Indeed,it was found that pre-computing such random samples actually led to overtraining. The reward function given by (5) was used to determine the policy$'$s utility,with $\alpha =0.1$,$\beta =1.0$,and $\delta =0.001$. The selection of the weights in the reward function was set by trial and error. A higher importance was given to an accurate soft landing as compared to fuel efficiency. Higher values of the fuel weight would force the system to trade fuel efficiency for position and velocity accuracy,resulting in a harder landing. Importantly,position utility was weighted less than the velocity as the position altitude component is always zero at the end of the landing phase. The optimization algorithm was set up to start with a step size of 0.04 and to remain in each epoch until 500 consecutive iterations resulted in no utility improvement.
|
|
Table Ⅱ OPTIMIZATION ENVIRONMENT |
At the end of the optimization phase,the utility was found to be $-$0.46,with a position component of $-$0.01,a velocity component of $-$0.25,and a fuel component of $-$0.20. The worst case landing state is reported in Table Ⅲ.
|
|
Table Ⅲ WORST CASE LANDING STATE AFTER OPTIMIZATION |
No significant problems with overtraining were observed during the policy optimization,although occasionally,a later epoch will exhibit slightly worse performance (measured using novel inputs) than an earlier epoch. It is possible that this is just due to the stochastic nature of the search algorithm,and the utility (measured using novel inputs) might have increased again if the search was allowed to continue. The lack of any problem with over fitting is likely due to the fact that RL,as opposed to supervised learning (as in the pre-training,apprentice learning phase),uses a utility metric that does not attempt to associate "correct" actions directly with a given state input. Instead,the utility metric is structured around some desired behavior,and the policy optimization algorithm has considerable latitude in choosing the best action for a given state. For this reason,RL is sometimes referred to as "semi-supervised" learning. Conversely,supervised learning uses a cost function that is some measure of the error between the design matrix and target matrix. Overtraining results when the learning algorithm uses its degrees of freedom to minimize this error at the expense of higher error for novel inputs. Because of overtraining, supervised learning can therefore result in very good results for the training points but poor results for novel inputs. Moreover, since the optimization was conducted with simulated noise,each set of weights is evaluated with a slightly different set of trajectories. As shown in Fig. 6,most of the optimization progress occurs early on,with acceptable performance being obtained after 6 000 iterations.

|
Download:
|
| Fig. 6. Utility as function of the numbers of iterations. | |
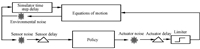
The RL-based landing guidance algorithm is tested using a set of Monte Carlo simulations executed to evaluate the overall performance of the proposed approach when the guidance algorithm is confronted with novel states not encountered during policy optimization. A schematic of the components employed in the simulator is shown in Fig. 7. Here,the limiter comes into play if the norm of the thrust vector output by the policy exceeds either the engine$'$s minimum or maximum thrust allowable during the powered descent phase. The simulator uses a 0.01 s time step and the 4${\rm th}$ order Runge-Kutta integration,and the guidance loop is established to operate at 100 Hz.
|
Download:
|
| Fig. 7. Simulation environment. | |
1000 Monte Carlo simulations were executed over four different sets of simulation parameters,as shown in Table Ⅳ. The results are reported in Table Ⅴ. Each simulation has randomized initial conditions distributed over the ranges as described in Table I. For Cases 1 $\sim$ 3,margin was added to the initial conditions (1 m/s for the velocity dimensions and 10 m for the downrange dimension) to insure that the lander guided descent did not start at the edge of known state space. For Case 4,the margin was increased to 2 m/s for the velocity dimensions and 20 m for the downrange dimension.
|
|
Table Ⅳ CASE DESCRIPTIONS |
|
|
Table Ⅴ SIMULATION RESULTS |
All cases resulted in a soft pinpoint landing. Fuel usage (see last column of Table Ⅴ) has been defined as the ratio of simulated fuel consumption to the fuel consumption computed solving the open-loop guidance landing problem via GPOPS. Although the guidance algorithm performs well in terms of accuracy and soft landing,it is sub-optimal with respect to fuel consumption. Indeed,the RL-based guidance algorithm produced closed-loop trajectories almost 8 s longer than the expected open-loop (deterministic) optimal trajectories. This is likely due to the low sampling resolution (22 samples per trajectory) employed to generate the training set. To investigate the issue further,a new policy was optimized over a slightly smaller state space obtained by removing the worst outliers obtained after the neural network training phase. The resulting policy exhibited a slightly improved fuel usage (1.12 times the optimal baseline for (Case 1). With this in mind,it is possible that if performing apprenticeship learning using a training set with a higher sampling resolution results in fewer outliers,fuel efficiency --- as measured following stochastic optimization --- may improve. Interestingly,fuel consumption slightly improved as the noise level was increased. The latter is probably related to the consequent increase in landing velocity.
A set of 10 000 Monte Carlo simulations have been run for the single Case 4. Histograms of the resulting landing position and velocity are shown in Figs. 8 and 9. To show the feasibility of dynamic retargeting,Case 4 simulations were re-run,and retargeted the landing site by shifting it +/$-$100 m downrange at an altitude of 1000 m,+/$-$10 m downrange at an altitude of 100 m,and +/$-$1 m downrange at an altitude of 10 m. The results were unchanged from the case without retargeting. Plots of a sample trajectory from Case 4 are shown in Fig. 10. The noisy thrust experienced by the lander is due to the mass flow rate variation.

|
Download:
|
| Fig. 8. Histogram of landing velocity: 10 000 samples, Case 4. | |

|
Download:
|
| Fig. 9. Histogram of landing position: 10 000 samples, Case 4. | |

|
Download:
|
| Fig. 10. Case 4 (worst case noise) telemetry. | |
Note that increasing environmental,actuator,and sensor noise does not have a significant impact on performances over the range tested. Indeed,large perturbations experienced by the lander$'$s current (true) position are likely to result in a measured position that is still within the policy$'$s known state space,still allowing the guidance algorithm to drive the system to a soft,pinpoint landing. However,when the noise increases to a level that pushes the lander outside the known state space,the performance rapidly deteriorates. Nevertheless,such a scenario can be made less likely to occur by adding operating margin in the design phase. Even with larger margins,there are still noise limits beyond which the RL-based landing guidance algorithm fails to provide a soft landing. To get an estimate of the noise bounds,100m of margin in the downrange direction and 10 m/s of margin for each component of the velocity vector were added. Subsequently,the noise level has been increased according to the values shown in Table Ⅵ. A new set of 1 000 Monte Carlo simulations were executed under these conditions. The latter results in a mean,standard deviation, and maximum norm of landing velocity of 0.467 m/s,0.114 m/s,and 1.08 m/s respectively,and a mean,standard deviation,and maximum norm of landing position of 0.229 m,0.107 m,and 0.54m, respectively. This puts the lander just past the 1 m/s limit for a soft landing.
|
|
Table Ⅵ NOISE LEVELS FOR EXTREME NOISE SIMULATION |
In order to compare the RL performance to current practice,we implemented the Apollo guidance algorithm[5, 19]. This guidance algorithm follows a trajectory computed as a quartic polynomial,and uses proportional and derivative control to close the loop. The advantage of this approach is that within certain limits,a trajectory can be computed during the flight,allowing precision landing and dynamic retargeting. In this case,the trajectory is determined using a single reference point,which is the desired landing position,velocity,and acceleration,which are all zero in the target centered reference frame. For this special case,the guidance law is given by (14):
| $ \begin{align} {{\pmb T}}=12\frac{{{{\pmb R}{\pmb T}{\pmb G}}}(t_{go} )-{{{\pmb R}{\pmb G}}}}{t^2_{go} }+6\frac{{{{\pmb V}{\pmb T}{\pmb G}}}(t_{go} )+{{{\pmb V}{\pmb G}}}}{t_{go} }, \end{align} $ | (14) |
where ${\pmb T}$ is the thrust vector,$t_{go} =-\frac{1}{2}\frac{{{\pmb V}{\pmb G}}_z \sqrt {{{\pmb V}{\pmb G}}_z ^2+16{{\pmb R}{\pmb G}}_z g} }{g}$ is the negative time to go, ${{{\pmb R}{\pmb T}{\pmb G}}}$,and ${{{\pmb V}{\pmb T}{\pmb G}}}$ are the target position vector and velocity vector,respectively, and ${{\pmb R}{\pmb G}}$ and ${{\pmb V}{\pmb G}}$ are the current position and velocity vectors,respectively. Note that ${{\pmb V}{\pmb G}}_z $ indicates the elevation component of the current velocity vector,and $g$ is the acceleration of gravity on Mars. For a soft surface landing,both ${{\pmb R}{\pmb T}{\pmb G}}$ and ${{\pmb V}{\pmb T}{\pmb G}}$ were set to the zero vector.
The Apollo guidance algorithm was evaluated by executing a set of Monte Carlo simulations using the same cases as for the RL algorithm (Table Ⅳ). The simulation time step was set to 1 ms. Random initial conditions were computed identically as with the RL guidance law testing,with the exception that the powered descent phase began at 2 000 m rather than 1 500 m. This change was necessary because the Apollo guidance law did not perform well when the downrange initial condition was much greater than the elevation initial condition. This is likely due to the fact that time-to-go is calculated using vertical distance and velocity components only.
Importantly,it was found that limiting the thrust as was done when simulating RL guidance caused the lander to crash. By trial and error,it was found that the Apollo guidance required twice the maximum thrust capability as the RL guidance.
In all cases,the Apollo guidance was able to achieve a slightly better positional precision as compared to the RL guidance. However the RL guidance law achieved softer landings,i.e.,less impact velocity,in the presence of noise. However,the Apollo-like guidance failed under the same thrust-limiting conditions for which the RL guidance was designed to operate.
E. Results Over the Extended State-Space and Real-time ImplementationTo analyze how well this algorithm scales,the extent of the downrange dimension of the state space has been increased to range from $-$1 060 m to $-$2 950 m. In this case,a neural network with 64 hidden layer nodes was trained via apprentice learning on the above mentioned state space using open-loop optimal trajectories[21]. The policy was subsequently optimized in the RL framework. Due to the larger state space employed in training,its computational time was increased. The simulated initial conditions employed in policy iteration used 4 evenly spaced samples over each of the velocity dimensions and 15 evenly spaced samples over the downrange position dimension. The results are reported in Table Ⅶ. Case numbers refer to Table Ⅳ. In this case pinpoint soft landing is achieved with deteriorated performance. The deterioration in performance was likely due to the sparser training cases employed over the extended space. Indeed,the sampling resolution should have been increased in the downrange dimension; the extent of this dimension was almost five times higher than with the smaller state space,but the number of samples along this dimension was only increased by a factor of three. Nevertheless,performance degraded gracefully.
|
|
Table Ⅶ SIMULATION RESULTS OVER EXTENDED STATE SPACE |
The development of a RL-based guidance algorithm resulted in a neural network trained to approximate a policy (acceleration command) that is optimal in a stochastic environment. Such network is extremely suitable for real-time implementation on the onboard micro-processor. Although the training phase is fairly computational intensive,once trained,the network output is determined by a relatively small number of matrix multiplications and function evaluations. The weight of the neurons can be easily stored on the on-board memory and employed during the descent phase to generate the feedback command. The RL guidance has been designed and simulated to operate with 100 Hz guidance cycle. Considering the amount of operations required by the network, generating an acceleration command with such frequency should be feasible and within the standard practice of realistic guidance systems.
Ⅴ. CONCLUSIONSIn this paper,a novel guidance algorithm for Mars powered descent is presented. Following the dictates of the RL theory,the landing problem is formulated as an MDP,and apprenticeship learning followed by a policy optimization procedure is employed to design an optimal landing guidance algorithm that ensures pinpoint landing, fuel efficiency and robustness against environmental uncertainties and un-modeled dynamics. During the powered descent phase,the guidance algorithm employs currently available (estimated) state information (i.e.,position and velocity) to take an optimal action. Ultimately,this sequence of optimal actions results in a pinpoint soft landing. Moreover,within certain reasonable constraints,the RL-based landing guidance algorithm can dynamically retarget the spacecraft to a new landing site multiple times during the powered descent phase,opening the possibility of online optimal landing site selection. The proposed guidance algorithm was tested using a set of Monte Carlo simulations over a range of non-ideal conditions, including actuator delay,actuator,sensor,and environmental noise. The controller is shown to be reasonably robust under such non-ideal conditions. A clear advantage of the RL approach to control problems is that the guidance algorithm can be optimized in a simulation environment that includes factors such as noise and system delays. Another advantage is that the RL approach can be used even when the environmental dynamics are too complex to model deterministically, and must be approximated with a stochastic model.
To the best of our knowledge,this is the first time that the RL framework is employed to devise guidance algorithms for planetary landing. The vertical (2-D) landing problem has been specifically chosen to provide the literature with a proof-of-concept study that shows the power of the RL-based methodology as applied to such problems. The design approach could be easily extended to a 3-D landing guidance problem which may result in a larger network (i.e.,larger number of nodes) and consequently larger training times.
Importantly,in this study,although thrust limitation constraints have been explicitly incorporated in the learning and verification process,the RL-based guidance algorithm has not been designed to explicitly account for specific glide-slope and/or additional attitude constraints. The implementation of the apprentice training approach allow the generation of an initial set of weights that explicitly try to approximate the acceleration command that is the solution of a constrained optimal control problem (i.e.,capable of enforcing specific thrust angle constraints,see Appendix A). However, during the policy training such constraints are not specifically enforced. Attitude constraints may be important for landing systems specifically equipped with terrain-relative navigation systems that require the navigation sensor to be pointed at the surface within specified limits. In such cases,the RL approach could be extended to account for constraints. For example,one could enforce limits on the thrust direction by explicitly solving a constrained optimization problem during the training phase. Nevertheless,since the navigation approach is function of the mission architecture,the attitude-unconstrained problem as presented in this study has a value on its own. Indeed,for a short powered descent,one can possibly conceive landing systems architectures employing optical sensors to establish an accurate position at the beginning of the powered descent phase and then navigate via accelerometers which do not impose specific attitude constraints.
Future work will investigate the effect of training the neural network on higher resolution trajectories,increasing the size of the state space,and applying RL for full-scale 6-DOF landing controllers. In addition,RL-based guidance algorithms could be potentially applied to other space exploration problems,including hovering during asteroids close-proximity operations, hypersonic re-entry,final powered descent while deploying a sky-crane,as well as attaining a desired orbit from the surface as required in a sample return mission.
Appendix AApprenticeship learning is implemented by training a neural network to learn the relationship between the lander state (position and velocity) and thrust command. Such a relationship can be determined by numerically computing a set of open-loop,fuel-optimal landing guidance solutions.The minimum-fuel optimal guidance problem can be formulated as follows[37].
Minimum-fuel problem: Find the thrust program that minimizes the following cost function (negative of the lander final mass; equivalent to minimizing the amount of propellant during descent):
| $ \begin{align} \max _{t_F ,T_C (.)} m_L (t_F )=\min _{t_F ,T_C (.)} \int_0^{t_F } {\left\| {{{T}}_{{C}} } \right\|} \mbox{ }{\rm d}t, \end{align} $ | (A1) |
subject to the following constraints (equations of motion):
| $ \begin{align} &\ddot {r}_L =-{\rm g}_M +\frac{T_C}{m_L},\end{align} $ | (A2) |
| $\begin{align} & \frac{\rm d}{{\rm d}t}m_L =-\frac{\left\| {T_C } \right\|}{I_{spg_0 } }, \end{align} $ | (A3) |
and the following boundary conditions and additional constraints:
| $ \begin{align}& 0 < T_{\min } < \left\| {T_C } \right\| < T_{\max } \end{align} $ | (A4) |
| $ \begin{align} & {\pmb r}_{L} (0)={\pmb r}_{L0} ,\quad {\pmb v}_{L} (0)={\dot {\pmb r}}_{L} (0)={\pmb v}_{L0},\end{align} $ | (A5) |
| $ \begin{align} &{\pmb r}_{L} (t_F )={\pmb r}_{LF} ,\quad {\pmb v}_{L} (t_F )={\dot {\pmb r}}_{L} (t_F )={\pmb v}_{L}F, \end{align} $ | (A6) |
| $\begin{align} & m_L (0)\!=\!m_{Lwet} ,~~ \vartheta_{alt} (t)=\tan ^{-1}\left( \frac{\sqrt {\pmb r}_{Lx}^2 +{\pmb r}_{Ly} ^2 }{\pmb r}_{Lz} \right)\le \vartheta _{alt}. \end{align} $ | (A7) |
Here,the thrust is limited to operate between a minimum value ($T_{\min } )$ and a maximum value ($T_{\max } $). An additional constraint on the flight path angle (A7) is imposed such that the altitude angle is never less than a prescribed value $\vartheta _{alt} $ ("glide slope" constraint). The problem formulated in (A1) $\sim$ (A7) does not have an analytical solution and must be solved numerically. To obtain the open-loop,fuel-optimal thrust program,the GPOPS has been employed. GPOPS is an open-source optimal control software that implements Gauss and Radau hp-adaptive pseudospectral methods. After formulating the landing problem as described above,the software allows the direct transcription of the continuous-time,fuel-optimal control problem to a finite-dimensional nonlinear programming problem (NLP). In GPOPS, the resulting NLP is solved using the sparse nonlinear optimizer (SNOPT) solver[38]. The pseudospectral approach is very powerful as it allows one to approximate both state and control using a basis of lagrange polynomials. Moreover,the dynamics is collocated at the Legendre-Gauss-Radau points. The use of global polynomials coupled with Gauss quadrature collocation points is known to provide accurate approximations that converge exponentially to continuous problems with smooth solutions.
The open-loop fuel-optimal landing problem is solved assuming that the motion of the lander is constrained to occur in a vertical plane (altitude and downrange). The lander initial altitude is kept fixed at 1 500 m whereas the initial downrange is varied between $-$4 000 m to $-$500 m. Initial vertical velocity ranges between $-$40 m/s and $-$75 m/s whereas the initial downrange velocity ranges between 60 and 100 m/s. The lander is assumed to weigh 1900 kg (wet mass) and is capable of a maximum (allowable) thrust of 13 258 N as well as a minimum (allowable) thrust of 4 972 N. The terminal position is set to be at the origin of the MSF frame to be achieved with zero velocity (soft landing). No glide slope constraints have been implemented to generate the training set. Examples of open-loop,fuel-optimal training trajectories and the corresponding optimal velocity field are reported in Fig. 2.
| [1] | Steltzner A, Kipp D, Chen A, Burkhart D, Guernsey C, Mendeck G,Mitcheltree R, Powell R, Rivellini T, San Martin M, Way D. Marsscience laboratory entry, descent, and landing system. In: Proceedingsof the 2006 IEEE Aerospace Conference. Big Sky, MT: IEEE, 2006. |
| [2] | Shotwell R. Phoenix-the first Mars scout mission. Acta Astronautica,2005, 57(2-8): 121-134 |
| [3] | Singh G, SanMartin A M, Wong E C. Guidance and control design forpowered descent and landing on Mars. In: Proceedings of the 2006 IEEEAerospace Conference. Big Sky, MT: IEEE, 2007. 1-8 |
| [4] | Klumpp A R. Apollo Guidance, Navigation, and Control: Apollo Lunar-Descent Guidance. Massachusetts Institute of Technology, Charles StarkDraper Lab, TR R-695, Cambridge, MA, 1971. |
| [5] | Klumpp A R. Apollo lunar descent guidance. Automatica, 1974, 10(2):133-146 |
| [6] | Chomel C T, Bishop R H. Analytical lunar descent guidance algorithm.Journal of Guidance, Control, and Dynamics, 2009, 32(3): 915-926 |
| [7] | Furfaro R, Selnick S, Cupples M L, Cribb M W. Non-linear slidingguidance algorithms for precision lunar landing (AAS 11-167). In:Proceedings of the 21st AAS/AIAA Space Flight Mechanics Meeting.San Diego, CA: American Astronautical Society by Univelt, 2011.945-964 |
| [8] | Bishop C M. Pattern Recognition and Machine Learning. Berlin, Heidelberg:Springer, 2006. |
| [9] | Calise A J, Rysdyk R T. Nonlinear adaptive flight control using neuralnetworks. IEEE Control Systems Magazine, 1998, 18(6): 14-25 |
| [10] | Sutton R S, Barto A G. Reinforcement Learning: An Introduction.Cambridge, MA: MIT Press, 1998. 100-103 |
| [11] | Gaudet B, Furfaro R. Adaptive Pinpoint and Fuel Efficient Mars Landingusing Reinforcement Learning (AAS 12-191). In: Proceeding of the 22ndSpaceflight Mechanics Meeting. San Diego, CA: American AstronauticalSociety by Univelt, 2012. 1309-1328 |
| [12] | Ng A Y, Kim H J, Jordan M I, Sastry S. Autonomous helicopter flightvia reinforcement learning. Advances in Neural Information ProcessingSystems 16. Cambridge, MA: MIT Press, 2004. |
| [13] | Ng A. CS229 Lecture Notes, Stanford University [Online], available:http://cs229.stanford.edu/materials.html, July 9, 2012 |
| [14] | Munos R, Szepesv′ari C. Finite-time bounds for fitted value iteration.Journal of Machine Learning Research, 2008, 1: 815-857 |
| [15] | Powell W B. Approximate Dynamic Programming: Solving the Cursesof Dimensionality (Second edition). Hoboken, N.J.: Wiley, 2011. |
| [16] | Bishop C M. Pattern Recognition and Machine Learning. Berlin, Heidelberg:Springer, 2006. |
| [17] | Koller D, Friedman N. Probabilistic Graphical Models. Massachusetts:MIT Press, 2009. |
| [18] | Ochshorn J. Calculate with pressure [Online], available: http://courses.cit.cornell.edu/arch264/calculators/example2.4/index.html, July9, 2012 |
| [19] | Tuckness D G. Analysis of a terminal landing on Mars. Journal ofSpacecraft and Rockets, 1995, 32(1): 142-148 |
| [20] | Coates A, Abbeel P, Ng A Y. Learning for control from multipledemonstrations. In: Proceedings of the 25th International Conferenceon Machine Learning. New York, USA: ACM, 2008. 144-151 |
| [21] | Huntington G T. Advancement and Analysis of Gauss PseudospectralTranscription for Optimal Control Problems [Ph. D. dissertation], MassachusettsInstitute of Technology, Cambridge MA, 2007 |
| [22] | Françolin C C, Benson D A, Hager W W, Rao A V. Costate approximationin optimal control using integral Gaussian quadrature orthogonalcollocation methods. Optimal Control Applications and Methods, to bepublished |
| [23] | Patterson M A, Hager W W, Rao A V. A ph mesh refinement methodfor optimal control. Optimal Control Applications and Methods, to bepublished |
| [24] | Patterson M A, Rao A V. GPOPS-II: a MATLAB software for solvingmultiple-phase optimal control problems using Hp-adaptive Gaussianquadrature collocation methods and sparse nonlinear programming.ACM Transactions on Mathematical Software, 2013, 39(3), Article 1 |
| [25] | Patterson M A, Rao A V. Exploiting sparsity in direct collocationpseudospectral methods for solving optimal control problems. Journalof Spacecraft and Rockets, 2012, 49(2): 354-377 |
| [26] | Darby C L, Garg D, Rao A V. Costate estimation using multiple-intervalpseudospectral methods. Journal of Spacecraft and Rockets, 2011, 48(5):856-866 |
| [27] | Darby C L, Hager W W, Rao A V. An Hp-adaptive pseudospectralmethod for solving optimal control problems. Optimal Control Applicationsand Methods, 2011, 32(4): 476-502 |
| [28] | Garg D, Patterson M A, Françolin C, Darby C L, Huntington G T,Hager W W, Rao A V. Direct trajectory optimization and costate estimationof finite-horizon and infinite-horizon optimal control problemsusing a Radau pseudospectral method. Computational Optimization andApplications, 2011, 49(2): 335-358 |
| [29] | Darby C L, Hager W W, Rao A V. Direct trajectory optimization using avariable low-order adaptive pseudospectral method. Journal of Spacecraftand Rockets, 2011, 48(3): 433-445 |
| [30] | Garg D, Hager W W, Rao A V. Pseudospectral methods for solvinginfinite-horizon optimal control problems. Automatica, 2011, 47(4):829-837 |
| [31] | Rao A V, Benson D A, Darby C, Patterson M A, Francolin C, SandersI, Huntington G T. Algorithm 902: GPOPS, A MATLAB softwarefor solving multiple-phase optimal control problems using the Gausspseudospectral method. ACM Transactions on Mathematical Software,2010, 37(2), Article 22 |
| [32] | MacKay D J C. Bayesian interpolation. Neural Computation, 1992, 4(3):415-447 |
| [33] | Rumelhart D E, Hinton G E, Williams R J. Learning representations byback-propagating errors. Nature, 1986, 323(6088): 533-536 |
| [34] | Gonz´alez R. Neural Networks for Variational Problems in Engineering[Ph.D dissertation], University of Catalonia, Spain, 2008 |
| [35] | Spall J C. Introduction to Stochastic Search and Optimization. New York:Wiley, 2003. |
| [36] | Fu M C. What you should know about simulation and derivatives. NavalResearch Logistics (NRL), 2008, 55(8): 723-736 |
| [37] | Acikmese B, Ploen S R. Convex programming approach to powereddescent guidance for mars landing. Journal of Guidance, Control, andDynamics, 2007, 30(5): 1353-1366 |
| [38] | Gill P E, Murray W, Saunders M A. SNOPT: an SQP algorithm for largescaleconstrained optimization. SIAM Review, 2005, 47(1): 99-131 |
 2014, Vol.1
2014, Vol.1 

