2. College of Science and Engineering, Texas A&M University, TX 78414, USA;
3. Department of Electrical & Computer Engineering, Missouri University of Science and Technology, MO 65401, USA
OPTIMAL control has been one of the key topics in control engineering for over half a century due to both theoretical merit and practical applications. Traditionally,for infinite-horizon optimal regulation of linear systems with linear-quadratic regulator (LQR),a constant solution to the algebraic Riccati equation (ARE) can be found,provided that the system dynamics is known[1, 2] which is subsequently utilized to obtain the optimal policy. For general nonlinear systems,the optimal solution can be obtained by solving the Hamilton-Jacobi-Bellman (HJB) equation,which,however,is not an easy task since the HJB equation normally does not have an analytical solution.
In last few decades,with full state feedback,reinforcement learning methodology is widely used by many researchers to address the optimal control under the infinite-horizon scenario for both linear and nonlinear systems[3, 4, 5, 6, 7, 8]. However,in many practical situations,the system state vector is difficult or expensive to measure. Therefore,several traditional nonlinear observers,such as high-gain or sliding mode observers,have been developed during the past few decades[9, 10]. However,the above mentioned observer designs are applicable to systems which are expressed in a specific system structure such as Brunovsky-form,and require the system dynamics to be a priori.
The optimal regulation of nonlinear systems can be addressed either for infinite or finite-horizon scenario. The finite-horizon optimal regulation still remains unresolved due to the following reasons. First,the solution with the optimal control of finite-horizon nonlinear system becomes essentially time-varying thus complicating the analysis,in contrast with the infinite-horizon case,where the solution is time-independent. In addition,the terminal constraint is explicitly imposed in the cost function,whereas in the infinite-horizon case,the terminal constraint is normally ignored. Finally,addition of online approximators,such as NNs to approximate the system dynamics and generate an approximate solution to the time-dependent HJB equation in a forward-in-time manner while satisfying the terminal constraint as well as closed-loop stability,is quite involved.
The past literature[11, 12, 13, 14] provides some insights into solving finite-horizon optimal regulation of nonlinear system. The developed techniques either function backward-in-time[11, 12] or require offline training[13, 14] with iteration-based approach. However,backward-in-time solution hinders the real time implementation,while inadequate number of iterations will lead to instability of the system[6]. Further,the state vector is needed in all these techniques[11, 12, 13, 14]. Therefore,a finite-horizon optimal regulation scheme,which can be implemented in an online and forward-in-time manner with completely unknown system dynamics and without using both state measurements and value/policy iterations,is yet to be developed.
Motivated by the aforementioned deficiencies,in this paper,an extended Luenberger observer is first proposed to estimate the system state vector as well as the control coefficient matrix, thus relaxing the need for a separate identifier to reconstruct the control coefficient matrix. Next,the actor-critic architecture is utilized to generate the near optimal control policy,wherein the value function is approximated by using critic NN while the near optimal policy is generated by using the approximated value function and the control coefficient matrix of observer. It is important to note that since the proposed scheme approximates the HJB equation solution by using NNs,derived control policy is based on near optimal control input .
To handle the time-varying nature of the solution to the HJB equation or the value function,the NNs with constant weights and time-varying activation functions are utilized. Additionally,in contrast with [13] and [14],the control policy is updated once a sampling instant and hence the policy/value iterations are not performed. An error term corresponding to the terminal constraint is defined and minimized over time such that the terminal constraint can be properly satisfied. A novel update law for tuning NN is developed such that the critic NN weights will be tuned not only by using Bellman error but also the terminal constraint error. Finally,stability of our proposed design scheme is demonstrated by using Lyapunov stability analysis.
Therefore,the contribution of this paper involves developing a novel approach to near optimal control of uncertain nonlinear discrete-time systems in affine form,which is based on finite-horizon output feedback in an online and forward-in-time manner without utilizing value or policy iterations. An online NN-based observer is introduced to generate the state vector and control coefficient matrix thus relaxing the need for an explicit identifier. This online observer is utilized along with the time-based adaptive critic controller for generating online optimal control. Tuning laws for all the NNs are also derived,and the stability of system is demonstrated by Lyapunov theory.
The rest of the paper is organized as follows. In Section II, background and formulation of finite-horizon optimal control for affine nonlinear discrete-time systems are introduced. In Section III,the control design scheme along with the stability analysis is addressed. In Section IV,simulation results are given. Conclusive remarks are provided in Section V.
Ⅱ. BACKGROUNDConsider the following nonlinear system:
| $ \begin{align} \label{eq1} \begin{array}{l} {{ x}}_{k+1} =f({{ x}}_k )+g({{ x}}_k ){{ u}}_k ,\\ {{ y}}_k ={{C x}}_k ,\\ \end{array} \end{align} $ | (1) |
where ${{ x}}_k \in \Omega _{{ x}} \subset R ^n$, ${{ u}}_k \in \Omega _{{ u}} \subset R ^m$ and ${{ y}}_k \in \Omega _{{ y}} \subset R ^p$ are the system states,control inputs and system outputs,respectively, $f({{ x}}_k )\in R ^n$,$g({ { x}}_k )\in R ^{n\times m}$ are smooth unknown nonlinear dynamics,and ${{ C}}\in R ^{p\times n}$ is the known output matrix. Before proceeding,the following assumption is needed.
Assumption 1. The nonlinear system given in (1) is considered to be controllable and observable. Moreover,the system output ${{ y}}_k \in \Omega _{{ y}} $ is measurable and the control coefficient matrix $g({{ x}}_k )$ is bounded in a compact set such that $0 < \left\| {g({{ x}}_k )} \right\|_F < g_{M} $,where $\left\| \cdot \right\|_F $ denotes the Frobenius norm and $g_{M} $ is a positive constant.
The objective of the optimal control design is to determine a feedback control policy that minimizes the following time-varying value or cost function given by
| $ \begin{align} \label{eq2} V({{ x}}_k ,k)=\phi ({{ x}}_{N} )+\sum\limits_{i=k}^{{N}-1} {L{(}{{ x}}_i {,}{{ u}}_i ,i{)}}, \end{align} $ | (2) |
where $[k,{N}]$ is the time interval of interest,$\phi ({{ x}}_{N} )$ is the terminal constraint that penalizes the terminal state ${{ x}}_{N} $,$L{(}{{ x}}_k {,}{{ u}}_k ,k{)}$ is the cost-to-go function at each time step $k$ and takes the quadratic form as $L{(}{{ x}}_k {,}{{ u}}_k ,k{)}={{ x}}_k^{\rm T} {{Q}}_k {{ x}}_k +{ { u}}_k^{\rm T} {{R}}_k {{ u}}_k $,where ${{Q}}_k \in R ^{n\times n}$,${{R}}_k \in R ^{m\times m}$ are positive semi-definite and positive definite symmetric weighting matrices, respectively. Setting $k={N}$,the terminal constraint for the value function is given as
| $ \begin{align} \label{eq3} V({{ x}}_{N} ,{N})=\phi ({{ x}}_{N} ). \end{align} $ | (3) |
Remark 1. Generally,the terminal constraint $\phi ({ { x}}_{N} )$ is a function of state at terminal stage ${N}$ and is not necessarily in quadratic form. In the case of standard linear quadratic regulator (LQR),$\phi ({ { x}}_{N} )$ takes the quadratic form as $\phi ({{ x}}_{N} )={{ x}}_{N}^{\rm T} {{Q}}_{N} {{ x}}_{N} $ and the optimal control policy can be obtained by solving the Riccati equation (RE) in a backward-in-time fashion from the terminal value ${{Q}}_{N}$.
It is important to note that in the case of finite-horizon,the value function (2) becomes essentially time-varying,in contrast with the infinite-horizon case[6, 7, 8]. By Bellman$'$s principle of optimality[1, 2],the optimal cost from $k$ onwards is equal to
| $ \begin{align} \label{eq4} V^\ast ({{ x}}_k ,k)=\mathop {\min }\limits_{{{ u}}_k } \left\{ {L{(}{{ x}}_k {,}{{ u}}_k {)}+V^\ast ({{ x}}_{k+1} ,k+1)} \right\}. \end{align} $ | (4) |
The optimal control policy ${{ u}}_k^\ast $,which minimizes the value function $V^\ast ({{ x}}_k ,k)$,is obtained by using the stationarity condition $\partial {V^ * }({x_k},k){\rm{ }}/\partial {u_k} = 0$ and comes out to be[2]
| $ \begin{equation} \label{eq5} {{ u}}_k^\ast =-\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )\frac{\partial V^\ast ({{ x}}_{k+1} ,k+1)}{\partial {{ x}}_{k+1} }. \end{equation} $ | (5) |
From (5),it is clear that even when the full system state vector and dynamics are available,the optimal control cannot be obtained for the nonlinear discrete-time system due to the requirement of future state vector ${{ x}}_{k+1} $. To avoid this drawback and relax the requirement for system dynamics,iteration-based schemes are normally utilized by using NNs with offline training[15].
However,iteration-based schemes are not preferred for implementation,since the number of iterations within a sampling interval cannot be easily determined to ensure the stability[6]. Moreover,the iterative approaches cannot be implemented when the system dynamics is completely unknown,as control coefficient matrix $g({{ x}}_k )$ is at least required for the control policy[7]. To overcome the need for the measured state vector,an optimal control scheme is used in this paper with measured outputs with the system dynamics unknown and iterative approach not utilized,as given in the next section.
Ⅲ. FINITE-HORIZON NEAR OPTIMAL REGULATOR DESIGN WITH OUTPUT FEEDBACKIn this section,the output feedback based finite-horizon near optimal regulation scheme for nonlinear discrete-time systems in affine form,with completely unknown system dynamics,is addressed. First,due to the unavailability of the system states and uncertain system dynamics,an extended version of Luenberger observer is proposed to reconstruct both the system states and control coefficient matrix in an online manner,provided the observer converges faster or at the same speed as that of the controller. Thus the proposed observer design relaxes the need for an explicit identifier. Next,the reinforcement learning methodology is utilized to approximate the time-varying value function with actor-critic structure,while both NNs are represented by constant weights and time-varying activation functions. In addition,an error term corresponding to the terminal constraint is defined and minimized over time so that the terminal constraint can be properly satisfied. The stability of the closed-loop system is demonstrated by Lyapunov theory to show that the parameter estimation error remains bounded as the system evolves.
A. Observer DesignThe system dynamics (1) can be reformulated as
| $ \begin{equation} \label{eq6} \begin{array}{l} {{ x}}_{k+1} ={{Ax}}_k +F({{ x}}_k )+g({{ x}}_k ){{ u}}_k ,\\ {{ y}}_k ={{C{ x}}}_k ,\\ \end{array} \end{equation} $ | (6) |
where ${{A}}\in R ^{n\times n}$ is a Hurwitz matrix such that $({{A}},{{C}})$ is observable,and $F({{ x}}_k )=f({{ x}}_k )-{{A{ x}}}_k $. NN has been proven to be an effective method in the estimation and control of nonlinear systems due to its online learning capability[16]. According to the universal approximation property[17],the system states can be represented by using NN on a compact set $\Omega $ as
| $ \begin{align} & {{ x}}_{k+1} ={{A{ x}}}_k +F({{ x}}_k )+g({{ x}}_k ){{ u}}_k =\notag\\ &\quad {{A{ x}}}_k +{{W}}_F^{\rm T} \sigma _F ({ { x}}_k )+{{W}}_g^{\rm T} \sigma _g ({{ x}}_k ){{ u}}_k +{{ \varepsilon }}_{Fk} +{{ \varepsilon }}_{gk} {{ u}}_k =\notag\\ & \quad {{A{ x}}}_k +\left[{{\begin{array}{*{20}c} {{{W}}_F } \\ {{{W}}_g } \\ \end{array} }} \right]^{\rm T}\left[{{\begin{array}{*{20}c} {\sigma _F ({{ x}}_k )} & {{ 0}} \\ {{ 0}} & {\sigma _g ({{ x}}_k )} \\ \end{array} }} \right]\left[{{\begin{array}{*{20}c} 1 \\ {{{ u}}_k } \\ \end{array} }} \right]+\notag\\ &\quad[{\begin{array}{*{20}c} {{{ \varepsilon }}_{Fk} } & {{{ \varepsilon }}_{gk} } \\ \end{array} }]\left[{{\begin{array}{*{20}c} 1 \\ {{{ u}}_k } \\ \end{array} }} \right] =\notag\\ & \quad {{A{ x}}}_k +{{W}}^{\rm T}\sigma ({{ x}}_k ){\bar{ {u}}}_k +{\bar{ {\varepsilon }}}_k , \end{align} $ | (7) |
where ${{W}}=\left[{{\begin{array}{*{20}c} {{{W}}_F } \\ {{{W}}_g } \\ \end{array} }} \right]\in R ^{L\times n}$,$\sigma ({{ x}}_k )=\left[{{\begin{array}{*{20}c} {\sigma _F ({{ x}}_k )} & {{ 0}} \\ {{ 0}} & {\sigma _g ({{ x}}_k )} \\ \end{array} }} \right]\in R ^{L\times (1+m)}$,${\bar{ {u}}}_k =\left[{{\begin{array}{*{20}c} 1 \\ {{{ u}}_k } \\ \end{array} }} \right]\in R ^{(1+m)}$ and ${\bar{ {\varepsilon }}}_k =[{\begin{array}{*{20}c} {{{ \varepsilon }}_{Fk} } & {{{ \varepsilon }}_{gk} } \\ \end{array} }]{\bar{ {u}}}_k \in R ^n$,with $L$ being the number of hidden neurons. In addition,the target NN weights, activation function and reconstruction error are assumed to be bounded as $\left\| {{W}} \right\|\le W_{M} $,$\left\| {\sigma ({{ x}}_k )} \right\|\le \sigma _{M} $ and $\left\| {{\bar{ {\varepsilon }}}_k } \right\|\le \bar {\varepsilon }_{M} $,where $W_{M} $,$\sigma _{M} $ and $\bar {\varepsilon }_{M} $ are positive constants. Then,the system state vector ${{ x}}_{k+1} ={{A{ x}}}_k +F({{ x}}_k )+g({ { x}}_k ){{ u}}_k $ can be identified by updating the target NN weight matrix ${{W}}$.
Since the real system states are unavailable for the controller, we propose the following extended Luenberger observer described by
| $ \begin{equation} \label{eq8} \begin{array}{l} {\hat{ {x}}}_{k+1} ={{A\hat {{ x}}}}_k +{\hat{ {W}}}_k^{\rm T} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k +{{L}}({{ y}}_k -{{C\hat {{ x}}}}_k ),\\ { \hat{ {y}}}_k ={{C\hat {{ x}}}}_k ,\\ \end{array} \end{equation} $ | (8) |
where ${\hat{{W}}}_k $ is the estimated value of the target NN weights ${{W}}$ at each time step $k$,${\hat{ {x}}}_k $ is the reconstructed system state vector,$\hat {{ y}}_k $ is the estimated output vector and ${{L}}\in R ^{n\times p}$ is the observer gain selected by the designer.
Now define and express the state estimation error as
| $ \begin{align} & { }{\tilde{ {x}}}_{k+1} ={{ x}}_{k+1} -{\hat{ {x}}}_{k+1} =\notag\\ & \quad {{A{ x}}}_k +{{W}}^{\rm T}\sigma ({{ x}}_k ){\bar{ {u}}}_k +{\bar{ {\varepsilon }}}_k -\notag\\ &\quad({{A\hat {{ x}}}}_k +{\hat{{W}}}_{k+1}^{\rm T} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k +{{ L}}({ { y}}_k -{{C\hat {{ x}}}}_k )) =\notag\\ & \quad {{A}}_c {\tilde{ {x}}}_k +{\tilde{{W}}}_k^{\rm T} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k +{{W}}^{\rm T}\tilde {\sigma }({{ x}}_k ,{\hat{ {x}}}_k ){\bar{ {u}}}_k +{\bar{ {\varepsilon }}}_k= \notag\\ &\quad { }{{A}}_c {\tilde{ {x}}}_k +{\tilde{ {W}}}_k^{\rm T} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k +{\bar{ {\varepsilon }}}_{Ok} , \end{align} $ | (9) |
where ${{A}}_c ={{A}}-{{LC}}$ is the closed-loop matrix, ${\tilde{{W}}}_k ={{W}}-{\hat{{W}}}_k $ is the NN weight estimation error,$\tilde {\sigma }({{ x}}_k ,{ \hat{ {x}}}_k )=\sigma ({{ x}}_k )-\sigma ({\hat{ {x}}}_k )$ and ${\bar{{ \varepsilon }}}_{Ok} ={{W}}^{\rm T}\tilde {\sigma }({{ x}}_k ,{\hat{ {x}}}_k ){\bar{ {u}}}_k $ $+{\bar{ {\varepsilon }}}_k $ are bounded terms due to the bounded values of ideal NN weights,activation functions and reconstruction errors.
Remark 2. It should be noted that the proposed observer (8) differs from the past literature[18, 19] in two essential aspects. First,the observer with a single NN presented in (8) generates the reconstructed system states for the controller design. Second,the control coefficient matrix $g({{ x}}_k )$ can be estimated from the proposed observer which is utilized in the near optimal control design shown in the next section.
Now select the tuning law for the NN weights as
| $ \begin{equation} \label{eq10} {\hat{{W}}}_{k+1} =(1-\alpha _{I} ){\hat{{W}}}_k +\beta _{I} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k {\tilde { {y}}}_{k+1}^{\rm T} {{l}}^{\rm T}, \end{equation} $ | (10) |
where $\alpha _{I} >0$,$\beta _{I} >0$ are the tuning parameters, ${\tilde{ {y}}}_{k+1} ={{ y}}_{k+1} -{\hat{ {y}}}_{k+1} $ is the output error,and ${{l}}\in R ^{n\times p}$ is selected to match the dimension[20]. It is important to notice that the first term of (10) ensures the stability of the observer weight estimation error,while the second term in (10) utilizes the output error (the only information we have) to tune the observer NN weights in order to guarantee the stability of the observer. The observer gain,$L$,and the tuning parameters have to be carefully selected to ensure faster convergence of the observer than that of the controller.
Next,by recalling from (9),the NN weight estimation error dynamics comes out to be
| $ \begin{align} & {\tilde{ {W}}}_{k+1} ={{W}}-{\hat{{W}}}_{k+1} =\notag\\ &\quad(1-\alpha _{I} ){\tilde{ {W}}}_k +\alpha _{I} {{ W}}-\beta _{I} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k {\tilde{ {y}}}_{k+1}^{\rm T} {{ l}}^{\rm T} =\notag\\ &\quad(1-\alpha _{I} ){\tilde{ {W}}}_k +\alpha _{I} {{ W}}-\beta _{I} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k {\tilde{ {x}}}_k^{\rm T} {{ A}}_c^{\rm T} {{ C}}^{\rm T}{{ l}}^{\rm T} -\notag\\ & \quad\beta _{I} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k {\bar{ {u}}}_k^{\rm T} \sigma ^{\rm T}({\hat{ {x}}}_k ){\tilde{{W}}}_k {{C}}^{\rm T}{{ l}}^{\rm T} -\notag\\ &\quad\beta _{I} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k {\bar{ {\varepsilon }}}_{Ok}^{\rm T} { {C}}^{\rm T}{{ l}}^{\rm T}. \end{align} $ | (11) |
Next,the boundedness of the NN weight estimation error ${{ \tilde {W}}}_k $ will be demonstrated in Theorem 1. However,before proceeding further,the following definition is required.
Definition 1[17]. An equilibrium point ${{ x}}_e $ is said to be uniformly ultimately bounded (UUB) if there exists a compact set $\Omega _{{ x}} \subset R ^n$ so that for all initial state ${{ x}}_0 \in \Omega _{{ x}} $,there exists a bound $B$ and a time $T(B,{{ x}}_0 )$ such that $\left\| {{{ x}}_k -{{ x}}_e } \right\|\le B$ for all $k\ge k_0 +T$.
Theorem 1 (Boundedness of the observer error). Let the nonlinear system (1) be controllable and observable and the system output,${{ y}}_k \in \Omega _{{ y}} $,be measurable. Let the initial NN observer weights ${\hat{ {W}}}_k $ be selected from the compact set $\Omega _{OB} $ which contains the ideal weights ${{W}}$. Given an initial admissible control input,${{ u}}_0 \in \Omega _{ u} $,let the proposed observer be given by (8) and the update law for tuning the NN weights be given by (10). Then, there exist positive constants $\alpha _{I} $ and $\beta _{I} $ satisfying $(2 - \sqrt 2 )/2{\rm{ < }}{\alpha _I} < 1$ and $0 < \beta _{I} < \frac{2(1-\alpha _{I} )\lambda _{\min } ({{lC}})}{\left\| {\sigma ({\hat{ {x}}}_k ){ \bar{ {u}}}_k } \right\|^2+1}$,with $\lambda _{\min } $ denoting the minimum eigenvalue,such that the observer error ${\tilde { {x}}}_k $ and the NN weight estimation errors ${\tilde {{W}}}_k $ are all UUB, with the bounds given by (A6) and (A7).
Proof. See Appendix.
B. Near Optimal Controller DesignIn this subsection,we present the finite-horizon near optimal regulator which requires neither the system state vector nor the system dynamics. The reason why we consider this design being near optimal rather than optimal is due to the observer NN reconstruction errors. Based on the observer design proposed in Section III-A,the feedback signal for the controller only requires the reconstructed state vector ${\hat{ {x}}}_k $ and the control coefficient matrix generated by the observer. To overcome the drawback of dependency on the future value of system states as (5) stated in Section II,reinforcement learning based methodology with an actor critic structure is adopted to approximate the value function and control inputs individually.
The value function is obtained approximately by using the temporal difference error in reinforcement learning while the optimal control policy is generated by minimizing this value function. The time-varying nature of the value function and control inputs are handled by utilizing the NNs with constant weights and time-varying activation functions. In addition,the terminal constraint in the cost function can be properly satisfied by defining and minimizing a new error term corresponding to the terminal constraint $\phi ({{ x}}_{N} )$ over time. As a result,the proposed algorithm performs in an online and forward-in-time manner which enjoys great practical benefits.
According to the universal approximation property of NNs[17] and actor-critic methodology[21],the value function and control inputs can be represented by a "critic" NN and an "actor" NN,respectively,as
| $ \begin{equation} \label{eq12} V({{ x}}_k ,k)={{W}}_V^{\rm T} \sigma _V ({{ x}}_k ,k)+\varepsilon _V ({{ x}}_k ,k) \end{equation} $ | (12) |
and
| $ \begin{equation} \label{eq13} {{ u}}({{ x}}_k ,k)={{W}}_{{ u}}^{\rm T} \sigma _{{ u}} ({{ x}}_k ,k)+\varepsilon _{{ u}} ({ { x}}_k ,k), \end{equation} $ | (13) |
where ${{W}}_V \in R ^{L_V }$ and ${{W}}_{ { u}} \in R ^{L_{{ u}} \times m}$ are constant target NN weights, with $L_V $ and $L_{{ u}} $ being the number of hidden neurons for critic and actor network,$\sigma _V ({{ x}}_k ,k)\in R ^{L_V }$ and $\sigma _{{ u}} ({{ x}}_k ,k)\in R ^{L_{{ u}} }$ are the time-varying activation functions,$\varepsilon _V ({ { x}}_k ,k)\in R $ and $\varepsilon _{{ u}} ({{ x}}_k ,k)\in R ^m$ are the NN reconstruction errors for the critic and action network, respectively. Under standard assumption[17],the target NN weights are considered bounded such that $\left\| {{{W}}_V } \right\|\le W_{V{M}} $ and $\left\| {{{W}}_{{ u}} } \right\|\le W_{{{ u}}{M}} $,respectively,where both $W_{V{M}} $ and $W_{{{ u}}{M}} $ are positive constants[17]. The NN activation functions and the reconstruction errors are also assumed to be bounded such that $\left\| {\sigma _V ({{ x}}_k ,k)} \right\|\le \sigma _{V{M}} $,$\left\| {\sigma _{{ u}} ({{ x}}_k ,k)} \right\|\le \sigma _{{{ u}}{M}} $,$\left| {\varepsilon _V ({{ x}}_k ,k)} \right|\le \varepsilon _{V{M}} $ and $\left| {\varepsilon _{{ u}} ({{ x}}_k ,k)} \right|\le \varepsilon _{{{ u}}{M}} $,with $\sigma _{V{M}} $,$\sigma _{{{ u}}{M}} $, $\varepsilon _{V{M}} $ and $\varepsilon _{{{ u}}{M}} $ being all positive constants[17]. In addition,in this work,the gradient of the reconstruction error is also assumed to be bounded such that $\left\| {\partial {\varepsilon _{V,k}}/\partial {x_{k + 1}}} \right\| \le {\varepsilon _{V{M^\prime }}}$, with $\varepsilon _{V{M}}' $ being a positive constant[7].
The terminal constraint of the value function is defined,similar to (12),as
| $ \begin{equation} \label{eq14} V({{ x}}_{N} ,{N})={{W}}_V^{\rm T} \sigma _V ({ { x}}_{N} ,{N})+\varepsilon _V ({{ x}}_{N} ,{N}), \end{equation} $ | (14) |
where $\sigma _V ({{ x}}_{N} ,{N})\in R $ and $\varepsilon _V ({{ x}}_{N} ,{N})\in R $ represent the activation and construction error corresponding to the terminal state ${ { x}}_{N} $,respectively.
Remark 3. The fundamental difference between this work and [13] is that our proposed scheme yields a completely forward-in-time and online solution without using value/policy iteration or offline training,whereas the scheme proposed in [13] is essentially an iteration-based direct heuristic dynamic programming (DHDP) scheme and the NN weights are trained offline. In addition,state availability is also relaxed in this work.
1)Value function approximation: According to (12),the time-varying value function $V({{ x}}_k ,k)$ can be approximated by using a NN as
| $ \begin{equation} \label{eq15} \hat {V}({\hat{ {x}}}_k ,k)={\hat{ {W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_k ,k), \end{equation} $ | (15) |
where $\hat {V}({\hat{ {x}}}_k ,k)$ represents the approximated value function at time step $k$. ${\hat{ {W}}}_{Vk} $ and $\sigma _V ({ \hat{ {x}}}_k ,k)$ are the estimated critic NN weights and "reconstructed" activation function with the estimated state vector ${ \hat{ {x}}}_k $ as the inputs.
The value function at the terminal stage can be represented by
| $ \begin{equation} \label{eq16} \hat {V}({{ x}}_{N} ,{N})={\hat{{W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_{N} ,{N}), \end{equation} $ | (16) |
where ${\hat{ {x}}}_{N} $ is an estimation of the terminal state. It should be noted that since the true value of ${{ x}}_{N} $ is not known,${\hat{ {x}}}_{N} $ can be considered as an "estimate" of ${ { x}}_{N} $ and can be chosen randomly as long as ${ \hat{ {x}}}_{N} $ lies within a region for a stabilizing control policy[8, 13].
To ensure optimality,the Bellman equation should hold along the system trajectory. According to the principle of optimality,the true Bellman equation is given by
| $ \begin{equation} \label{eq17} {{ x}}_k^{\rm T} {{Q}}_k {{ x}}_k +({{ u}}_k^\ast )^{\rm T}{{R}}_k {{ u}}_k^\ast +V^\ast ({{ x}}_{k+1} ,k+1)-V^\ast ({{ x}}_k ,k)=0. \end{equation} $ | (17) |
However,(17) no longer holds when the reconstructed system state vector ${\hat{ {x}}}_k $ and NN approximation are considered. Therefore,with estimated values,the Bellman equation (17) becomes
| $ \begin{align} & e_{{BO},k} ={\hat{{x}}}_k^{\rm T} {{Q\hat {{x}}}}_k +{{ u}}_k^{\rm T} {{ R{ u}}}_k +\hat {V}({\hat{ {x}}}_{k+1} ,k+1)-\hat {V}({\hat{ {x}}}_k ,k) =\notag\\ & \quad{\hat{ {x}}}_k^{\rm T} {{Q\hat { x}}}_k +{{ u}}_k^{\rm T} {{R{ u}}}_k +{\hat{{W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_{k+1} ,k+1)-\notag\\ &\quad{\hat{{W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_k ,k) ={\hat{ {x}}}_k^{\rm T} {{Q\hat { x}}}_k +{ { u}}_k^{\rm T} {{R{ u}}}_k -{\hat{{W}}}_{Vk}^{\rm T} \Delta \sigma _V ({\hat{ {x}}}_k ,k), \end{align} $ | (18) |
where $e_{{BO},k} $ is the Bellman equation residual error along the system trajectory,and $\Delta \sigma _V ({\hat{ {x}}}_k ,k)=\sigma _V ({\hat{ {x}}}_k ,k)-\sigma _V ({\hat{ {x}}}_{k+1} ,k+1)$. Next,using (16),define an additional error term corresponding to the terminal constraint as
| $ \begin{equation} \label{eq19} e_{{N},k} =\phi ({{ x}}_{N} )-{\hat{{W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_{N} ,{N}). \end{equation} $ | (19) |
The objective of the optimal control design is thus to minimize the Bellman equation residual error $e_{{BO},k} $ as well as the terminal constraint error $e_{{N},k} $,so that the optimality can be achieved and the terminal constraint can be properly satisfied. Next,based on gradient descent approach,the update law for critic NN can be defined as
| $ \begin{array}{l} {\widehat W_{Vk + 1}} = {\widehat W_{Vk}} + {\alpha _V}\frac{{\Delta {\sigma _V}({{\widehat x}_k},k){e_{BO,k}}}}{{1 + \Delta \sigma _V^{\rm{T}}({{\widehat x}_k},k)\Delta {\sigma _V}({{\widehat x}_k},k)}} + \\ \;\;\;\;\;\;\;\;\;\;\;{\alpha _V}\frac{{{\sigma _V}({{\widehat x}_N},N){e_{N,k}}}}{{1 + \sigma _V^{\rm{T}}({{\widehat x}_N},N){\sigma _V}({{\widehat x}_N},N)}}, \end{array} $ | (20) |
where $\alpha _V >0$ is a design parameter. Now define the NN weight estimation error as ${\tilde{{W}}}_{Vk} ={{W}}_V -{\hat{{W}}}_{Vk} $. Moreover,the observed system state should be persistently existing (PE)[5] for tuning critic NN. The standard Bellman equation (17) can be expressed by NN representation as
| $ \begin{equation} \label{eq21} 0={{ x}}_k^{\rm T} {{Q}}_k {{ x}}_k +({{ u}}_k^\ast )^{\rm T}{{R}}_k {{ u}}_k^\ast -{{W}}_V^{\rm T} \Delta \sigma _V ({{ x}}_k ,k)-\Delta \varepsilon _V ({{ x}}_k ,k), \end{equation} $ | (21) |
where $\Delta \sigma _V ({{ x}}_k ,k)=\sigma _V ({{ x}}_k ,k)-\sigma _V ({{ x}}_{k+1} ,k+1)$ and $\Delta \varepsilon _V ({ { x}}_k ,k)=\varepsilon _V ({{ x}}_k ,k)-\varepsilon _V ({{ x}}_{k+1} ,k+1)$.
Subtracting (18) from (21),$e_{{BO},k} $ can be further derived as
| $ \begin{align} & e_{{BO},k} ={\hat{ {x}}}_k^{\rm T} {{Q\hat { x}}}_k +{{ u}}_k^{\rm T} {{R{ u}}}_k -{\hat{ {W}}}_{Vk}^{\rm T} \Delta \sigma _V ({\hat{ {x}}}_k ,k) -\notag\\ & \quad{{ x}}_k^{\rm T} {{Q{ x}}}_k -({{ u}}_k^\ast )^{\rm T}{{R{ u}}}_k^\ast +{{W}}_V^{\rm T} \Delta \sigma _V ({{ x}}_k ,k)+\Delta \varepsilon _V ({{ x}}_k ,k) =\notag\\ & \quad{\hat{ {x}}}_k^{\rm T} {{Q\hat { x}}}_k +{{ u}}_k^{\rm T} {{R{ u}}}_k -{{ x}}_k^{\rm T} {{Q{ x}}}_k -({{ u}}_k^\ast )^{\rm T}{{R{ u}}}_k^\ast -\notag\\ & \quad{\hat{{W}}}_{Vk}^{\rm T} \Delta \sigma _V ({\hat{ {x}}}_k ,k)+{{W}}_V^{\rm T} \Delta \sigma _V ({\hat{ {x}}}_k ,k) -\notag\\ & \quad{{W}}_V^{\rm T} \Delta \sigma _V ({\hat{ {x}}}_k ,k)+{{W}}_V^{\rm T} \Delta \sigma _V ({{ x}}_k ,k)+\Delta \varepsilon _V ({{ x}}_k ,k) \le\notag\\ & \quad {\hat{ {x}}}_k^{\rm T} {{Q\hat { x}}}_k +{{ u}}_k^{\rm T} {{R{ u}}}_k -{{ x}}_k^{\rm T} {{Q{ x}}}_k -({{ u}}_k^\ast )^{\rm T}{{R{ u}}}_k^\ast +\notag\\ & \quad{\tilde{{W}}}_{Vk}^{\rm T} \Delta \sigma _V ({\hat{ {x}}}_k ,k){ }+{{W}}_V^{\rm T} \Delta \tilde {\sigma }_V ({{ x}}_k ,{\hat{ {x}}}_k ,k)+\Delta \varepsilon _V ({{ x}}_k ,k) \le\notag\\ & \quad L_m \left\| {{\tilde{ {x}}}_k } \right\|^2+{\tilde{ {W}}}_{Vk}^{\rm T} \Delta \sigma _V ({\hat{ {x}}}_k ,k){ }+\Delta \varepsilon _{VB} ({{ x}}_k ,k), \end{align} $ | (22) |
where $L_m $ is a positive Lipschitz constant for ${\hat{ {x}}}_k^{\rm T} {{Q}}_k {\hat{ {x}}}_k +{{ u}}_k^{\rm T} {{R}}_k {{ u}}_k -{{ x}}_k^{\rm T} {{Q}}_k {{ x}}_k -({{ u}}_k^\ast )^{\rm T}{{R}}_k {{ u}}_k^\ast $ due to the quadratic form in both system states and control inputs. In addition,$\Delta \tilde {\sigma }_V ({{ x}}_k ,{\hat{ {x}}}_k ,k)=\Delta \sigma _V ({{ x}}_k ,k)-\Delta \sigma _V ({\hat{ {x}}}_k ,k)$ and $\Delta \varepsilon _{VB} ({ { x}}_k ,k)={{W}}_V^{\rm T} \Delta \tilde {\sigma }_V ({{ x}}_k ,{\hat{ {x}}}_k ,k)+\Delta \varepsilon _V ({{ x}}_k ,k)$ are all bounded terms due to the boundedness of ideal NN weights, activation functions and reconstruction errors.
Recalling from (14),the terminal constraint error $e_{{N},k} $ can be further expressed as
| $ \begin{align} & e_{{N},k} =\phi ({{ x}}_{N} )-{\hat{{W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_{N} ,{N}) =\notag\\ & \quad{{W}}_V^{\rm T} \sigma _V ({{ x}}_{N} ,{N})+\varepsilon _V ({{ x}}_{N} ,{N})-{ \hat{{W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_{N} ,{N}) =\notag\\ & \quad{{W}}_V^{\rm T} \sigma _V ({{ x}}_{N} ,{N})-{{W}}_V^{\rm T} \sigma _V ({\hat{ {x}}}_{N} ,{N})+\varepsilon _V ({{ x}}_{N} ,{N}) +\notag\\ & \quad{{W}}_V^{\rm T} \sigma _V ({\hat{ {x}}}_{N} ,{N})-{\hat{{W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_{N} ,{N}) =\notag\\ & \quad{\tilde{{W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_{N} ,{N})+{{W}}_V^{\rm T} \tilde {\sigma }_V ({{ x}}_{N} ,{\hat{ {x}}}_{N} ,{N})+\varepsilon _V ({{ x}}_{N} ,{N}) =\notag\\ & \quad{\tilde{{W}}}_{Vk}^{\rm T} \sigma _V ({\hat{ {x}}}_{N} ,{N})+\varepsilon _{V{N}}, \end{align} $ | (23) |
where $\tilde {\sigma }_V ({{ x}}_{N} ,{\hat{ {x}}}_{N} ,{N})=\sigma _V ({{ x}}_{N} ,{N})-\sigma _V ({\hat{ {x}}}_{N} ,{N})$ and $\varepsilon _{V{N}} ={{W}}_V^{\rm T} \tilde {\sigma }_V ({{ x}}_{N} ,{\hat{ {x}}}_{N} ,{N})+\varepsilon _V ({{ x}}_{N} ,{N})$ are bounded due to bounded ideal NN weights,activation functions and reconstruction errors.
Finally,the error dynamics for the critic NN weights is
| $ \begin{align} & {\tilde{{W}}}_{Vk+1} ={\tilde{{W}}}_{Vk} -\alpha _V \frac{\Delta \sigma _V ({\hat{ {x}}}_k ,k)e_{{BO},k} }{1+\Delta \sigma _V^{\rm T} ({\hat{ {x}}}_k ,k)\Delta \sigma _V ({\hat{ {x}}}_k ,k)} -\notag\\ & \quad\alpha _V \frac{\sigma _V ({\hat{ {x}}}_{N} ,{N})e_{{N},k} }{1+\sigma _V^{\rm T} ({\hat{ {x}}}_{N} ,{N})\sigma _V ({\hat{ {x}}}_{N} ,{N})}. \end{align} $ | (24) |
Next,the boundedness of the critic NN weights will be demonstrated,as shown in the following theorem.
Theorem 2 (Boundedness of the critic NN weights). Let the nonlinear system (1) be controllable and observable and the system output,${{ y}}_k \in \Omega _{{ y}} $,be measurable. Let the initial critic NN weights ${\hat{{W}}}_{Vk} $ be selected from the compact set $\Omega _V $ which contains the ideal weights ${{W}}_V $. Let ${{ u}}_0 \in \Omega _{ u} $ be an initial admissible control input for system (1). Let the observed system state is PE[5],and the value function be approximated by a critic NN and the tuning law be given by (20). Then there exists a positive constant $\alpha _V $ satisfying $0 < \alpha _V < 1 {\left/ { {1 6}} \right. /} 6$ such that the critic NN weight estimation error ${\tilde{{W}}}_{Vk} $ is UUB with a computable bound $b_{{\tilde{{W}}}_V } $ given in (A16).
Proof. See Appendix.
2) Control input approximation: In this subsection,the near optimal control policy is obtained such that the estimated value function (15) is minimized. Recalling (13),the approximation of the control inputs by using a NN can be represented as
| $ \begin{equation} \label{eq25} {\hat{ {u}}}({\hat{ {x}}}_k ,k)={\hat{ {W}}}_{{ { u}}k}^{\rm T} \sigma _{{ u}} ({\hat{ {x}}}_k ,k), \end{equation} $ | (25) |
where ${\hat{ {u}}}({\hat{ {x}}}_k ,k)$ represents the approximated control input vector at time step $k,{\hat{ {W}}}_{{{ u}}k} $ and $\sigma _{{ u}} ({\hat{ {x}}}_k ,k)$ are the estimated values of the actor NN weights and "reconstructed" activation function with the estimated state vector ${\hat{ {x}}}_k $ as the input.
Define the control input error as
| $ \begin{equation} \label{eq26} {{ e}}_{{{ u}}k} ={\hat{ {u}}}({\hat{ {x}}}_k ,k)-{\hat{ {u}}}_1 ({\hat{ {x}}}_k ,k), \end{equation} $ | (26) |
where ${\hat{ {u}}}_1 ({\hat{ {x}}}_k ,k)=-\frac{1}{2}{ {R}}^{-1}\hat {g}^{\rm T}({\hat{ {x}}}_k )\nabla \hat {V}({ \hat{ {x}}}_{k+1} ,k+1)$ is the control policy that minimizes the approximated value function,$\hat {V}({\hat{ {x}}}_k ,k)$,$\nabla $ denotes the gradient of the estimated value function with respect to the system states, $\hat {g}({\hat{ {x}}}_k )$ is the approximated control coefficient matrix generated by the NN-based observer and $\hat {V}({\hat{ {x}}}_{k+1} ,k+1)$ is the approximated value function from the critic network.
Therefore,the control error (26) becomes
| $ \begin{align} & {{ e}}_{{{ u}}k} ={\hat{ {u}}}({\hat{ {x}}}_k ,k)-{\hat{ {u}}}_1 ({\hat{ {x}}}_k ,k) =\notag\\ & \quad{\hat{{W}}}_{{{ u}}k}^{\rm T} \sigma _{{ u}} ({\hat { {x}}}_k ,k)+\frac{1}{2}{{R}}^{-1}\hat {g}^{\rm T}({ \hat{ {x}}}_k )\nabla \sigma _V^{\rm T} ({\hat{ {x}}}_{k+1} ,k+1){\hat{{W}}}_{Vk} . \end{align} $ | (27) |
The actor NN weights tuning law is then defined as
| $ \begin{equation} \label{eq28} {\hat{{W}}}_{{{ u}}k+1} ={\hat{{W}}}_{{{ u}}k} -\alpha _{{ u}} \frac{\sigma _{{ u}} ({\hat{ {x}}}_k ,k){{ e}}_{{{ u}}k}^{\rm T} }{1+\sigma _{{ u}}^{\rm T} ({\hat{ {x}}}_k ,k)\sigma _{{ u}} ({\hat{ {x}}}_k ,k)}, \end{equation} $ | (28) |
where $\alpha _{{ u}} >0$ is a design parameter.
To find the error dynamics for the actor NN weights,first observe that
| $ \begin{align} & {{ u}}({{ x}}_k ,k)={{W}}_{{ u}}^{\rm T} \sigma _{{ u}} ({{ x}}_k ,k)+{{ \varepsilon }}_{\rm u} ({{ x}}_k ,k) = \\ & \quad-\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )(\nabla \sigma _V^{\rm T} ({{ x}}_{k+1} ,k+1){{W}}_V + \\ &\quad \nabla {{ \varepsilon }}_V ({{ x}}_{k+1} ,k+1)). \end{align} $ | (29) |
Or equivalently,
| $ \begin{align} & 0={{W}}_{{ u}}^{\rm T} \sigma _{{ u}} ({{ x}}_k ,k)+{{ \varepsilon }}_{{ u}} ({{ x}}_k ,k)+\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )\times \notag\\ &\quad { }\nabla \sigma _V^{\rm T} ({{ x}}_{k+1} ,k+1){{ W}}_V +\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )\nabla \varepsilon _V ({{ x}}_{k+1} ,k+1). \end{align} $ | (30) |
Subtracting (30) from (27),we have
| $ \begin{align} & {{ e}}_{{{ u}}k} ={\hat{{W}}}_{{{ u}}k}^{\rm T} \sigma _{{ u}} ({\hat{ {x}}}_k ,k) +\notag\\ &\quad { }\frac{1}{2}{{R}}^{-1}\hat {g}^{\rm T}({\hat{ {x}}}_k )\nabla \sigma _V^{\rm T} ({\hat{ {x}}}_{k+1} ,k+1){\hat {{W}}}_{Vk} -\notag\\ &\quad{ }{{W}}_{{ u}}^{\rm T} \sigma _{{ u}} ({{ x}}_k ,k)-{\bar{ {\varepsilon }}}_{{ u}} ({{ x}}_k ,k)- \notag\\ &\quad { }\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )\nabla \sigma _V^{\rm T} ({{ x}}_{k+1} ,k+1){{W}}_V- \notag\\ &\quad { }\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )\nabla \varepsilon _V ({{ x}}_{k+1} ,k+1) =\notag\\ &\quad-{\tilde{{W}}}_{{{ u}}k}^{\rm T} \sigma _{{ u}} ({\hat{ {x}}}_k ,k)-{{W}}_{{ u}}^{\rm T} \tilde {\sigma }_{{ u}} ({{ x}}_k ,{\hat{ {x}}}_k ,k)-{\rm \varepsilon }_{{ u}} ({{ x}}_k ,k) +\notag\\ &\quad { }\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )\nabla \sigma _V^{\rm T} ({\hat{ {x}}}_{k+1} ,k+1){\hat{ {W}}}_{Vk} +\notag\\ &\quad{ }\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )\nabla \tilde {\sigma }_V^{\rm T} ({{ x}}_{k+1} ,{\hat{ {x}}}_{k+1} ,k+1){\hat{{W}}}_{Vk} +\notag\\ & \quad \frac{1}{2}{{R}}^{-1}(\hat {g}^{\rm T}({\hat{ {x}}}_k )-g^{\rm T}({{ x}}_k ))\nabla \sigma _V^{\rm T} ({\hat{ {x}}}_{k+1} ,k+1){\hat{ {W}}}_{Vk} -\notag\\ &\quad { }\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )\nabla \sigma _V^{\rm T} ({{ x}}_{k+1} ,k+1){{W}}_V -\notag\\ &\quad { }\frac{1}{2}{{R}}^{-1}g^{\rm T}({{ x}}_k )\nabla \varepsilon _V ({{ x}}_{k+1} ,k+1), \end{align} $ | (31) |
where $\tilde {\sigma }_{{ u}} ({{ x}}_k ,{\hat{ {x}}}_k ,k)=\sigma _{{ u}} ({{ x}}_k ,k)-\sigma _{{ u}} ({\hat{ {x}}}_k ,k)$ and $ \nabla \tilde {\sigma }_V^{\rm T} ({{ x}}_{k+1} ,{\hat{ {x}}}_{k+1} ,k+1)=\nabla \sigma _V^{\rm T} ({{ x}}_{k+1} ,k+1)-\nabla \sigma _V^{\rm T} ({\hat{ {x}}}_{k+1} ,k+1).$
For simplicity,denote $\tilde {\sigma }_{{{ u}}k} =\tilde {\sigma }_{{ u}} ({{ x}}_k ,{\hat{ {x}}}_k ,k)$, $\nabla \hat {\sigma }_{Vk+1}^{\rm T} =\nabla \sigma _V^{\rm T} ({\hat{ {x}}}_{k+1} ,k+1)$,$\nabla \tilde {\sigma }_{Vk+1}^{\rm T} =\nabla \tilde {\sigma }_V^{\rm T} ({{ x}}_{k+1} ,{\hat{ {x}}}_{k+1} ,k+1)$,$\nabla \sigma _{Vk+1}^{\rm T} =\nabla \sigma _V^{\rm T} ({{ x}}_{k+1} ,k+1)$ and $\nabla \varepsilon _{Vk+1} =\nabla \varepsilon _V ({{ x}}_{k+1} ,k+1)$,then (31) can be further derived as
| $ \begin{array}{l} {e_{uk}} = - \widetilde W_{uk}^{\rm{T}}{\sigma _u}({\widehat x_k},k) - W_u^{\rm{T}}{{\tilde \sigma }_{uk}} - {\varepsilon _u}({x_k},k) + \\ \quad \frac{1}{2}{R^{ - 1}}{g^{\rm{T}}}({x_k})\nabla \sigma _{Vk + 1}^{\rm{T}}{W_V} - \frac{1}{2}{R^{ - 1}}{g^{\rm{T}}}({x_k})\nabla \sigma _{Vk + 1}^{\rm{T}}{\widetilde W_{Vk}} + \\ \quad \frac{1}{2}{R^{ - 1}}{g^{\rm{T}}}({x_k})\nabla \tilde \sigma _{Vk + 1}^{\rm{T}}{W_V} - \\ \;\;\;\frac{1}{2}{R^{ - 1}}{g^{\rm{T}}}({x_k})\nabla \tilde \sigma _{Vk + 1}^{\rm{T}}{\widetilde W_{Vk}} + \\ \quad \frac{1}{2}{R^{ - 1}}({{\hat g}^{\rm{T}}}({\widehat x_k}) - {g^{\rm{T}}}({\widehat x_k}))\nabla \hat \sigma _{Vk + 1}^{\rm{T}}{W_V} + \\ \quad \frac{1}{2}{R^{ - 1}}({g^{\rm{T}}}({\widehat x_k}) - {g^{\rm{T}}}({x_k}))\nabla \hat \sigma _{Vk + 1}^{\rm{T}}{W_V} - \\ \quad \frac{1}{2}{R^{ - 1}}({g^{\rm{T}}}({\widehat x_k}) - {g^{\rm{T}}}({x_k}))\nabla \hat \sigma _{Vk + 1}^{\rm{T}}{{\tilde W}_{Vk}} - \\ \quad \frac{1}{2}{R^{ - 1}}({g^{\rm{T}}}({\widehat x_k}) - {{\hat g}^{\rm{T}}}({\widehat x_k}))\nabla \hat \sigma _{Vk + 1}^{\rm{T}}{\widetilde W_{Vk}} - \\ \quad \frac{1}{2}{R^{ - 1}}{g^{\rm{T}}}({x_k})\nabla \sigma _{Vk + 1}^{\rm{T}}{W_V} - \frac{1}{2}{R^{ - 1}}{g^{\rm{T}}}({x_k})\nabla {\varepsilon _{Vk + 1}} = \\ \quad - \widetilde W_{uk}^{\rm{T}}{\sigma _u}({\widehat x_k},k) - \frac{1}{2}{R^{ - 1}}{g^{\rm{T}}}({x_k})\nabla \hat \sigma _{Vk + 1}^{\rm{T}}{\widetilde W_{Vk}} - \\ \quad \frac{1}{2}{R^{ - 1}}{{\tilde g}^{\rm{T}}}({\widehat x_k})\nabla \hat \sigma _{Vk + 1}^{\rm{T}}{W_V} - \\ \quad \frac{1}{2}{R^{ - 1}}({g^{\rm{T}}}({\widehat x_k}) - {g^{\rm{T}}}({x_k}))\nabla \hat \sigma _{Vk + 1}^{\rm{T}}{{\tilde W}_{Vk}} + \\ \quad \frac{1}{2}{R^{ - 1}}{{\tilde g}^{\rm{T}}}({\widehat x_k})\nabla \hat \sigma _{Vk + 1}^{\rm{T}}{\widetilde W_{Vk}} + {\overline \varepsilon _{uk}}, \end{array} $ | (32) |
where $\tilde {g}({\hat{ {x}}}_k )=g({\hat{ {x}}}_k )-\hat {g}({\hat{ {x}}}_k )$ and
| $ \begin{align} & {\bar{ {\varepsilon }}}_{{{ u}}k} =-{{ \varepsilon }}_{{ u}} ({{ x}}_k ,k)+\frac{1}{2}{{ R}}^{-1}g^{\rm T}({{ x}}_k )\nabla \tilde {\sigma }_{Vk+1}^{\rm T} {{W}}_V +\notag\\ &\qquad \frac{1}{2}{{R}}^{-1}(g^{\rm T}({\hat{ {x}}}_k )-g^{\rm T}({{ x}}_k ))\nabla \hat {\sigma }_{Vk+1}^{\rm T} {{W}}_V-\notag\\ &\qquad \frac{1}{2}{{ R}}^{-1}g^{\rm T}({{ x}}_k )\nabla \varepsilon _{Vk+1} -{{W}}_{{ u}}^{\rm T} \tilde {\sigma }_{{{ u}}k} \end{align} $ | (33) |
is bounded due to the bounded ideal NN weights,activation functions and reconstruction errors. Then the error dynamics for the actor NN weights are[7]
| $ \begin{equation} \label{eq33} {\tilde{ {W}}}_{{{ u}}k+1} ={\tilde{ {W}}}_{{{ u}}k} +\alpha _{{ u}} \frac{\sigma _{{ u}} ({\hat{ {x}}}_k ,k){{ e}}_{{{ u}}k}^{\rm T} }{1+\sigma _{{ u}}^{\rm T} ({\hat{ {x}}}_k ,k)\sigma _{{ u}} ({\hat{ {x}}}_k ,k)}. \end{equation} $ | (34) |
Remark 4. The update law for tuning the actor NN weights is based on gradient descent approach and it is similar to [7] with the difference that the estimated state vector ${\hat{ {x}}}_k $ is utilized as the input to the actor NN activation function instead of actual system state vector ${{ x}}_k $. In addition,the total error comprising Bellman error and terminal constraint error are utilized to tune the weights,whereas in [7] the terminal constraint is ignored. Further,optimal control scheme in this work utilizes identified control coefficient matrix $\hat {g}({\hat{ {x}}}_k )$,whereas in [7] control coefficient matrix $g({{ x}}_k )$ is assumed to be known. Due to these differences,stability analysis differs significantly from [7].
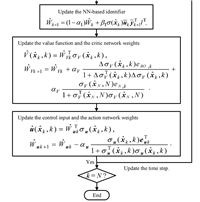
To complete this subsection,the flowchart of our proposed finite-horizon near optimal regulation scheme is shown in Fig. 1.
|
Download:
|
| Fig. 1. Flowchart of the proposed finite-horizon near optimal regulator. | |
3) Stability analysis: In this subsection,the system stability will be investigated. It will be shown that the overall closed-loop system remains bounded under the proposed near optimal regulator design. Before proceeding,the following lemma is needed
Lemma 1 (Bounds on the optimal closed-loop dynamics)[7]. Consider the nonlinear discrete-time system (1), then there exists an optimal control policy ${{ u}}_k^\ast $ such that closed-loop system dynamics $f({{ x}}_k )+g({ { x}}_k ){{ u}}_k^\ast $ can be written as
| $ \begin{equation} \label{eq34} \left\| {f({{ x}}_k )+g({{ x}}_k ){{ u}}_k^\ast } \right\|^2\le \rho \left\| {{{ x}}_k } \right\|^2, \end{equation} $ | (35) |
where $0 < \rho < 1$ is a constant.
Theorem 3 (Boundedness of the closed-loop system). Let the nonlinear system (1) be controllable and observable and the system output, ${{ y}}_k \in \Omega _{{ y}} $,be measurable. Let the initial NN weights for the observer,critic network and actor network,${\hat{ {W}}}_k$,${\hat{{W}}}_{Vk} $ and ${\hat{ {W}}}_{{{ u}}k} $ respectively be selected from the compact set $\Omega _{OB} $,$\Omega _V $ and $\Omega _{AN} $ which contain the ideal weights ${{W}}$,${{W}}_V$ and ${{W}}_{{ u}} $. Let ${{ u}}_0 ({{ x}}_k )\in \Omega _{{ u}} $ be an initial stabilizing control policy for (1),the observer system state,which is PE,be given by (8) and the NN weight update law for the observer,critic network and action network be provided by (10), (20) and (28),respectively. Then,there exist positive constants $\alpha _{I} $,$\beta _{I} $,$\alpha _V $,$\alpha _{{ u}} $, such that the observer error ${\tilde{ {x}}}_k $,the NN observer weight estimation errors ${\tilde{{W}}}_k $,critic and action network weights estimation errors ${\tilde{{W}}}_{Vk}$ and ${\tilde{{W}}}_{{{ u}}k} $ are all UUB,with the ultimate bounds given by (A20) $\sim $ (A23). Moreover,the estimated control input is bounded close to its optimal value such that $\left\| {{{ u}}^\ast ({ { x}}_k ,k)-{\hat{ {u}}}({\hat{ {x}}}_k ,k)} \right\|\le \varepsilon _{uo} $ for a small positive constant $\varepsilon _{uo} $.
Proof. See Appendix.
Ⅳ. SIMULATION RESULTSIn this section,a practical example is considered to illustrate our proposed near optimal regulation design scheme. Consider the Van der Pol oscillator with the dynamics given as
| $ \begin{equation} \label{eq35} \begin{array}{l} \dot {x}_1 =x_2 ,\\ \dot {x}_2 =(1-x_1^2 )x_2 -x_1 +u,\\ y=x_1 . \\ \end{array} \end{equation} $ | (36) |
The Euler method is utilized to discretize the system with a step size of $h=5 {\rm ms}.$
The weighting matrices in (2) are selected as ${{Q}}=\left[ {{\begin{array}{*{20}c} {0.1} & 0 \\ 0 & {0.1} \\ \end{array} }} \right]$ and ${{R}}=1$,while the Hurwitz matrix is selected as ${{A}}=\left[{{\begin{array}{*{20}c} {0.5} & {0.1} \\ 0 & {0.025} \\ \end{array} }} \right].$ The terminal constraint is chosen as $\phi ({{ x}}_{N} )=1$. For the NN setup,the inputs for the NN observer are selected as ${{ z}}_k =[{\hat{ {x}}}_k ,{ { u}}{ }_k]$. The time-varying activation functions for both the critic and actor networks are constructed as state-dependent and time-dependent parts (both the critic and actor NNs are constructed as the production of state-dependent part,$\sigma({ x},k)=\sigma_{ x}({ x})\cdot\sigma_t(\hat{k})$). The state-dependent part,$\sigma _{ x} ({ x})$,is chosen as expansion of even power polynomial as $\sigma _{ x} ({ x})=\{x_1^2 ,x_1 x_2 ,x_2^2 ,x_1^4 ,x_1^3 x_2 ,\cdots ,x_2^4 ,x_1^6 ,\cdots ,x_2^6 \}$. Moreover,the time-dependent part $\sigma _t (k)$ is also selected as even power polynomial as $\sigma _t (k)=\{1,[\exp (-\tau )]^2,$ $\cdots,[\exp (-\tau )]^{10},\cdots ,[\exp (-\tau )]^{10},[\exp (-\tau )]^8,\cdots,1\}$,with $\tau ={{(N}-k)} {\left/ { {{{(N}-k)} {N}}} \right. /} {N}$,the normalized time index.
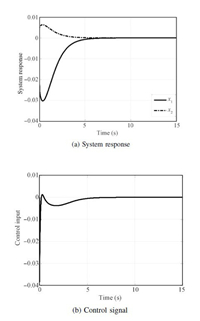
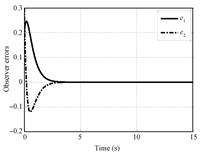
The simulations are shown as follows. First,the system response is shown in Fig. 2. Both system state vector and control input clearly converge close enough to the origin within finite time, which illustrates the stability of the proposed design scheme. The history of observer errors is also plotted in Fig. 3,which clearly shows the feasibility of proposed observer design. The observer errors converge quicker than the response of system. It is important to note that exploration noise (i.e.,$n\sim N(0,0.003))$ is added to the observer system state to ensure the PE requirement for tuning critic NN. Moreover,while the NN has been tuned properly,exploration noise has been removed since the PE condition is not needed. In this simulation example,critic NN and actor NN have been tuned and after around 2.5 s,based on Figs. 3 and 4,exploration noise has been removed which is also shown in Fig. 2 (b).
|
Download:
|
| Fig. 2. System response and control signal. | |
|
Download:
|
| Fig. 3. Observer error. | |
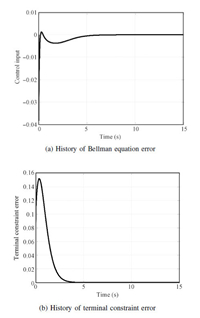
Next,the error history in the design procedure is given in Fig. 4. In Fig. 4 (a),the Bellman equation error converges close to zero within approximately 2.5 s,which illustrates the fact that the near optimality is indeed achieved. More importantly,the evolution of the terminal constraint error is shown in Fig. 4 (b). Convergence of the terminal constraint error demonstrates that the terminal constraint is also satisfied using our proposed design scheme.
|
Download:
|
| Fig. 4. Error history. | |
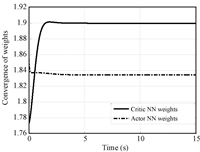
Next,the Frobenius norm of both critic NN and actor NN weights are shown in Fig. 5. It can be observed from the results that both weights converge and remain bounded,as desired.
|
Download:
|
| Fig. 5. Convergence of critic and actor NN weights. | |
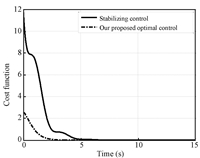
Finally,the comparison of the cost between a stabilizing control and our proposed near optimal control is given in Fig. 6. It can be seen clearly from the figure that both the costs converge to the terminal constraint $\phi ({{ x}}_{N} )=1$,while our design delivers a lower cost when compared with the non-optimal controller design.
|
Download:
|
| Fig. 6. Comparison of the costs. | |
In this paper,the reinforcement learning based finite-horizon near optimal regulator design is addressed by using output feedback for nonlinear discrete-time system in affine form with completely unknown system dynamics. Compared to the traditional finite-horizon optimal regulation design, the proposed scheme not only relaxes the requirement on availability of the system state vector and control coefficient matrix,but also functions in an online and forward-in-time manner instead of performing offline training and value/policy iterations.
The NN-based Luenberger observer relaxes the need for an additional identifier,while time-dependent nature of the finite-horizon is handled by a NN structure with constant weights and time-varying activation function. The terminal constraint is properly satisfied by minimizing an additional error term along the system trajectory. All NN weights are tuned online by using the proposed update laws,and Lyapunov stability theory demonstrates that the approximated control inputs converge close to their optimal values as time evolves. The performance of the proposed finite time near optimal regulator is demonstrated via simulation.
APPENDIXProof of Theorem 1. To show the boundedness of the proposed NN-based observer design,we need to show the observer error ${ {\tilde { x}}}_k $ and the NN weights estimation error ${{ \tilde {W}}}_k $ converge within an ultimate bound.
Consider the following Lyapunov candidate:
| $ \begin{align} L_{{IO}} (k)=L_{{\tilde{ {x}}},k} +L_{{\tilde{ {W}}},k} , \end{align} $ | (A1) |
where $L_{{\tilde{ {x}}},k} ={\tilde{ {x}}}_k^{\rm T} {\tilde { {x}}}_k $, $L_{{\tilde{ {W}}},k} ={\rm tr}\{{\tilde{{W}}}_k^{\rm T} {{\Lambda \tilde {W}}}_k \}$ with ${\rm tr}\{\cdot\}$ denoting the trace operator and ${{\Lambda }}={2(1+\chi _{\min }^2 ){{I}}} {\left/ { {{2(1+\chi _{\min }^2 ){{I}}} {\beta _{I} }}} \right. /} {\beta _{I} }$,where ${{ I}}\in R ^{L\times L}$ is an identity matrix and $0 < \chi _{\min }^2 < \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2$ is ensured to exist by the PE condition.
The first difference of $L_{{IO}} (k)$ is given by
| $ \begin{align}\Delta L_{{IO}} (k)=\Delta L_{{\tilde{ {x}}},k} +\Delta L_{{\tilde{ {W}}},k} . \end{align} $ | (A2) |
Next,we consider each term in (A2) individually. First,recall from the observer error dynamics (9),we have
| $ \begin{align} & \Delta L_{{\tilde{ {x}}},k} ={\tilde{ {x}}}_{k+1}^{\rm T} {\tilde{ {x}}}_{k+1} -{\tilde{ {x}}}_k^{\rm T} {\tilde{ {x}}}_k =\notag\\ &\quad{\tilde{ {x}}}_k^{\rm T} {{ A}}_c^{\rm T} {{ A}}_c {\tilde{ {x}}}_k +[\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k]^{\rm T}{\tilde{ {W}}}_k {\tilde{ {W}}}_k^{\rm T} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}} +\notag\\ &\quad{\bar{ {\varepsilon }}}_{Ok}^{\rm T} {\bar{ {\varepsilon }}}_{Ok} +2{\tilde{ {x}}}_k^{\rm T} {{ A}}_c^{\rm T} {\tilde{ {W}}}_k^{\rm T} \sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k +\notag\\ &\quad 2{\tilde{ {x}}}_k^{\rm T} {{ A}}_c^{\rm T} {\rm {\bf \bar {\varepsilon }}}_{Ok} +2{\bar{ {\varepsilon }}}_{Ok}^{\rm T} {\tilde{ {W}}}_k^{\rm T} \sigma ({ \hat{ {x}}}_k ){\bar{ {u}}}-{\tilde{ {x}}}_k^{\rm T} {\tilde{ {x}}}_k \le\notag\\ &\quad -(1-\gamma )\left\| {{\tilde{ {x}}}_k } \right\|^2+3\left\| {{\tilde{ {W}}}_k } \right\|^2\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2+3\left\| {{\bar{ {\varepsilon }}}_{Ok} } \right\|^2,\end{align} $ | (A3) |
where $\gamma =3\left\| {{{ A}}_c } \right\|^2$.
Now,recalling the NN weight estimation error dynamics (11),we have
| $ \begin{align} & \Delta L_{{\tilde{ {W}}},k} ={\rm tr}\{{\tilde{ {W}}}_{k+1}^{\rm T} {{ \Lambda \tilde {W}}}_{k+1} \}-{\rm tr}\{{ { \tilde { W}}}_k^{\rm T} {{ \Lambda \tilde {W}}}_k \} \le\notag\\ % &\quad { } 2(1-\alpha _{I} )^2{\rm tr}\{{\tilde{ {W}}}_k^{\rm T} {{ \Lambda \tilde {W}}}_k \}+6\alpha _{I}^2 \delta W_{M}^2 +\notag\\ % &\quad { }6\beta _{I}^2 \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{{ A}}_c } \right\|^2\left\| {{{ lC}}} \right\|^2\left\| {{\tilde{ {x}}}_k } \right\|^2 -\notag\\ &\quad { }4(1-\alpha _{I} )\beta _{I} \lambda _{\min } ({{lC}}){\tilde{ {W}}}_k^{\rm T} \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2{\tilde{ {W}}}_k +\notag\\ % &\quad{ }2\beta _{I}^2 \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{{ lC}}} \right\|^2\left\| {{\tilde{ {W}}}_k } \right\|^2+ \notag\\ &\quad { }6\beta _{I}^2\delta\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{{ lC}}} \right\|^2\left\| {{\bar{ {\varepsilon }}}_{Ok} } \right\|^2-{\rm tr}\{{\tilde{ {W}}}_k^{\rm T} {{ \Lambda \tilde {W}}}_k \}\le \notag\\ & \quad{ } -(1-2(1-\alpha _{I} )^2){\rm tr}\{{\tilde{ {W}}}_k^{\rm T} {{ \Lambda \tilde {W}}}_k \}+6\alpha _{I}^2 \delta W_{M}^2 +\notag \\ &\quad { }6\beta _{I}^2 \delta\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{{ A}}_c } \right\|^2\left\| {{{ lC}}} \right\|^2\left\| {{\tilde{ {x}}}_k } \right\|^2 -\notag\\ % &\quad { }2\beta _{I} ((1-\alpha _{I} )\lambda _{\min } ({{lC}})-\beta _{I} \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2)\delta \times \notag\\ &\quad { }\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{\tilde{ {W}}}_k } \right\|^2+6\beta _{I}^2 \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{ { lC}}} \right\|^2\left\| {{\bar{ {\varepsilon }}}_{Ok} } \right\|^2\le \notag\\ &\quad { }-(1-2(1-\alpha _{I} )^2)\delta \left\| {{\tilde{ {W}}}_k } \right\|^2+6\beta _{I}^2 \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\times \notag\\ &\quad { }\left\| {{{ A}}_c } \right\|^2\left\| {{{ lC}}} \right\|^2\left\| {{\tilde{ {x}}}_k } \right\|^2-2\beta _{I} ((1-\alpha _{I} )\lambda _{\min } ({{ lC}}) -\notag\\ &\quad { }\beta _{I} \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2)\delta \left\| {\sigma ({\hat { {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{\tilde{ {W}}}_k } \right\|^2+\varepsilon _{{WM}} ,\end{align} $ | (A4) |
where $\delta =\left\| {{ \Lambda }} \right\|$ and $\varepsilon _{{WM}} =6\alpha _{I}^2 \delta W_{M}^2 +6\beta _{I}^2 \delta \left\| {\sigma ({ \hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\times \left\| {{{ lC}}} \right\|^2\left\| {{\bar{ {\varepsilon }}}_{Ok} } \right\|^2$.
Therefore,by combining (A3) and (A4),the first difference of the total Lyapunov candidate is given as
| $ \begin{array}{l} \Delta {L_{IO}}(k) = \Delta {L_{\widetilde x,k}} + \Delta {L_{\widetilde W,k}} \le \\ \quad - (1 - \gamma ){\left\| {{{\widetilde x}_k}} \right\|^2} + 3{\left\| {{{\widetilde W}_k}} \right\|^2}{\left\| {\sigma ({{\widehat x}_k}){{\overline u }_k}} \right\|^2} + 3{\left\| {{{\overline \varepsilon }_{Ok}}} \right\|^2} - \\ \quad (1 - 2{(1 - {\alpha _I})^2})\delta {\left\| {{{\widetilde W}_k}} \right\|^2} - \frac{{2{\beta _I}\delta }}{{1 + {\chi _{{{\min }^2}}}}}{\left\| {{{\widetilde W}_k}} \right\|^2}{\left\| {\sigma ({{\widehat x}_k}){{\overline u }_k}} \right\|^2} + \\ \quad 2{\beta _I}\gamma {\left\| {lC} \right\|^2}\delta {\left\| {{{\widetilde x}_k}} \right\|^2} + {\varepsilon _{WM}} \le \\ \quad - (1 - (1 + 4{\left\| {lC} \right\|^2}(1 + {\chi _{{{\min }^2}}}))\gamma ){\left\| {{{\widetilde x}_k}} \right\|^2} + {\varepsilon _{OM}} - \\ \quad {\left\| {{{\widetilde W}_k}} \right\|^2}{\left\| {\sigma ({{\widehat x}_k}){{\overline u }_k}} \right\|^2} - (1 - 2{(1 - {\alpha _I})^2})\delta {\left\| {{{\widetilde W}_k}} \right\|^2}, \end{array} $ | (A5) |
where $\varepsilon _{{OM}} =3\left\| {{\bar{ {\varepsilon }}}_{Ok} } \right\|^2+\varepsilon _{{WM}} $. By standard Lyapunov stability theory,$\Delta L_{{IO},k} $ is less than zero outside a compact set as long as the following conditions hold:
| $ \begin{align} \left\| {{\tilde{ {x}}}_k } \right\|>\sqrt {\frac{\varepsilon _{{OM}} }{1-(1+4\left\| {{{ lC}}} \right\|^2(1+\chi _{\min }^2 ))\gamma }} \equiv b_{{\tilde{ {x}}}} ,\end{align} $ | (A6) |
or
| $ \begin{align}\left\| {{\tilde{ {W}}}_k } \right\|>\sqrt {\frac{\varepsilon _{{OM}} }{\chi _{\min }^2 +(1-2(1-\alpha _{I} )^2)\delta }} \equiv b_{{\tilde{ {W}}}} . \end{align} $ | (A7) |
Note that in (A6) the denominator is guaranteed to be positive, i.e.,$0 < \gamma < \frac{1}{1+4\left\| {{{ lC}}} \right\|^2(1+\chi _{\min }^2 )}$,by properly selecting the designed parameters ${{ A}}$,${ { L}}$ and ${{ l}}$.
Proof of Theorem 2. First,for simplicity,denote $\Delta \hat {\sigma }_{Vk} =\Delta \sigma _V ({\hat{ {x}}}_k ,k)$, $\Delta \varepsilon _{VBk} =\Delta \varepsilon _{VB} ({{ x}}_k ,k)$ and $\hat {\sigma }_{V{N}} =\sigma _V ({\hat{ {x}}}_{N} ,{N})$.
To show the boundedness of the critic NN weights estimation error ${\tilde{ {W}}}_{Vk} $,we consider the following Lyapunov candidate:
| $ \begin{align}L_{{\tilde{ {W}}}_V } (k)=L({\tilde{ {W}}}_{Vk} )+\Pi L({\tilde{ {x}}}_k )+\Pi L({\tilde{ {W}}}_k ),\end{align} $ | (A8) |
where $L({\tilde{ {W}}}_{Vk} )={\tilde{ {W}}}_{Vk}^{\rm T} {\tilde{ {W}}}_{Vk} $,$L({\tilde{ {x}}}_k )=({\tilde{ {x}}}_k^{\rm T} {\tilde{ {x}}}_k )^2$, $L({\tilde{ {W}}}_k )=({\rm tr}\{{\tilde{ {W}}}_k^{\rm T} {{ \Lambda \tilde {W}}}_k \})^2$ and $\Pi =\frac{\alpha _V (1+3\alpha _V )L_m^2 }{(1+\Delta \hat {\sigma }_{\min }^2 )(1-3\gamma ^2)}$.
Note that the second and the third terms in (A8) are needed in the proof due to the reason that the error dynamics for ${\tilde{ {W}}}_{Vk} $ are coupled with observer error ${\tilde{ {x}}}_k $ and the NN weights estimation error ${\tilde{ {W}}}_k $. We will show that dynamics for ${\tilde{ {x}}}_k $ and ${\tilde{ {W}}}_k $ will aid to prove the convergence of the critic NN weights estimation error ${\tilde{ {W}}}_{Vk} $.
Next,take each term in (A8) individually. The first difference of $L({\tilde{ {W}}}_{Vk} )$,by recalling (24),is given by
| $ \begin{align} & \Delta L({\tilde{ {W}}}_{Vk} )={\tilde{ {W}}}_{Vk+1}^{\rm T} {\tilde{ {W}}}_{Vk+1} -{\tilde{ {W}}}_{Vk}^{\rm T} {\tilde{ {W}}}_{Vk} =\notag\\ & \quad\left( {{\tilde{ {W}}}_{Vk} -\alpha _V \frac{\Delta \hat {\sigma }_{Vk} e_{{BO},k} }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }-\alpha _V \frac{\hat {\sigma }_{V{N}} e_{{N},k} }{1+\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} }} \right)^{\rm T}\times \notag\\ &\quad\left( {{\tilde{ {W}}}_{Vk} -\alpha _V \frac{\Delta \hat {\sigma }_{Vk} e_{{BO},k} }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }-\alpha _V \frac{\hat {\sigma }_{V{N}} e_{{N},k} }{1+\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} }} \right)-\notag\\ &~\quad{\tilde { {W}}}_{Vk}^{\rm T} {\tilde{ {W}}}_{Vk} =\notag\\ &\quad-2\alpha _V \frac{{\tilde{ {W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} e_{{BO},k} }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }-2\alpha _V \frac{{\tilde { {W}}}_{Vk}^{\rm T} \hat {\sigma }_{V{N}} e_{{N},k} }{1+\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} }+\notag\\ &~\quad { }\alpha _V^2 \frac{e_{{BO},k}^2 \Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }{(1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} )^2}+\alpha _V^2 \frac{e_{{N},k}^2 \hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} }{(1+\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} )^2}. \end{align} $ | (A9) |
With (22) and (23),the first difference of $L({\tilde{ {W}}}_{Vk} )$ can be further derived as
| $ \begin{align} & \Delta L({\tilde{ {W}}}_{Vk} )\le \notag\\ &\quad-2\alpha _V \frac{{\tilde{ {W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} (L_m \left\| {{\tilde { {x}}}_k } \right\|^2+{\tilde{ {W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} +\Delta \varepsilon _{VBk} )}{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} } -\notag\\ &\quad { }2\alpha _V \frac{{\tilde{ {W}}}_{Vk}^{\rm T} \hat {\sigma }_{V{N}} ({\tilde{ {W}}}_{Vk}^{\rm T} \hat {\sigma }_{V{N}} +\varepsilon _{V{N}} )}{1+\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} } +\notag\\ &\quad { }\alpha _V^2 \frac{(L_m \left\| {{\tilde{ {x}}}_k } \right\|^2+{\tilde{ {W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} +\Delta \varepsilon _{VBk} )^2\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }{(1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} )^2} +\notag\\ &\quad { }\alpha _V^2 \frac{({\tilde{ {W}}}_{Vk}^{\rm T} \hat {\sigma }_{V{N}} +\varepsilon _{V{N}} )^2\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} }{(1+\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} )^2} \le\notag\\ &\quad -2\alpha _V \frac{L_m {\tilde{ {W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} \left\| {{\tilde{ {x}}}_k } \right\|^2}{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }-2\alpha _V \frac{{\tilde {{W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} \Delta \hat {\sigma }_{Vk}^{\rm T} {\tilde{ {W}}}_{Vk} }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} } -\notag\\ &\quad { }2\alpha _V \frac{{\tilde{ {W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} \Delta \varepsilon _{VBk} }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }-2\alpha _V \frac{{\tilde{{W}}}_{Vk}^{\rm T} \hat {\sigma }_{V{N}} \hat {\sigma }_{V{N}}^{\rm T} {\tilde{ {W}}}_{Vk} }{1+\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} } -\notag\\ &\quad { }2\alpha _V \frac{{\tilde{ {W}}}_{Vk}^{\rm T} \hat {\sigma }_{V{N}} \varepsilon _{V{N}} }{1+\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} }+3\alpha _V^2 \frac{L_m^2 \left\| {{\tilde{ {x}}}_k } \right\|^4}{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} } +\notag\\ &\quad { }3\alpha _V^2 \frac{\Delta \varepsilon _{VBk}^2 }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }+3\alpha _V^2 \frac{{\tilde{ {W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} \Delta \hat {\sigma }_{Vk}^{\rm T} {\tilde{ {W}}}_{Vk} }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }+\notag\\ &\quad { }2\alpha _V^2 \frac{{\tilde{ {W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{V{N}} \Delta \hat {\sigma }_{V{N}}^{\rm T} {\tilde{ {W}}}_{Vk} }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }+2\alpha _V^2 \frac{\varepsilon _{V{N}}^2 }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }\le \notag\\ &\quad -\frac{\alpha _V (1-6\alpha _V )}{2}\frac{{\tilde{ {W}}}_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} \Delta \hat {\sigma }_{Vk}^{\rm T} {\tilde{ {W}}}_{Vk} }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }- \notag\\ &\quad { }\alpha _V (1-2\alpha _V )\frac{{\tilde{ {W}}}_{Vk}^{\rm T} \hat {\sigma }_{V{N}} \hat {\sigma }_{V{N}}^{\rm T} {\tilde{ {W}}}_{Vk} }{1+\hat {\sigma }_{V{N}}^{\rm T} \hat {\sigma }_{V{N}} }+ \notag\\ &\quad { }\alpha _V (1+3\alpha _V )\frac{L_m^2 \left\| {{\tilde{ {x}}}_k } \right\|^4}{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }+\varepsilon _{V{TM}}\le \notag\\ &\quad -\frac{\alpha _V (1-6\alpha _V )}{2}\frac{\Delta \hat {\sigma }_{\min }^2 }{1+\Delta \hat {\sigma }_{\min }^2 }\left\| {{\tilde{ {W}}}_{Vk} } \right\|^2- \notag\\ &\quad { }\alpha _V (1-2\alpha _V )\frac{\hat {\sigma }_{\min }^2 }{1+\hat {\sigma }_{\min }^2 }\left\| {{\tilde{ {W}}}_{Vk} } \right\|^2+ \notag\\ &\quad { }\frac{\alpha _V (1+3\alpha _V )}{1+\Delta \hat {\sigma }_{\min }^2 }L_m^2 \left\| {{\tilde{ {x}}}_k } \right\|^4+\varepsilon _{V{TM}} ,\end{align} $ | (A10) |
where
| $ \begin{align} & \varepsilon _{V{TM}} =\alpha _V (1+3\alpha _V )\frac{\Delta \varepsilon _{VBk}^2 }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }+\alpha _V (1+2\alpha _V )\times \notag\\ &\quad { }\frac{\varepsilon _{V{N}}^2 }{1+\Delta \hat {\sigma }_{Vk}^{\rm T} \Delta \hat {\sigma }_{Vk} }. \notag \end{align} $ |
Next,consider $L({\tilde{ {x}}}_k )$. Recall (A3) and apply Cauchy-Schwartz inequality,the first difference of $L({\tilde{ {x}}}_k )$ is given by
| $ \begin{array}{l} \Delta L({\widetilde x_k}) = {(\widetilde x_{k + 1}^{\rm{T}}{\widetilde x_{k + 1}})^2} - {(\widetilde x_k^{\rm{T}}{{\tilde x}_k})^2} \le \\ \quad \left[ { - (1 - \gamma ){{\left\| {{{\widetilde x}_k}} \right\|}^2} + 3{{\left\| {{{\widetilde W}_k}} \right\|}^2}{{\left\| {\sigma ({{\widehat x}_k}){{\overline u }_k}} \right\|}^2} + 3{{\left\| {{{\bar \varepsilon }_{Ok}}} \right\|}^2}} \right] \times \\ \quad \left[ {(1 + \gamma ){{\left\| {{{\widetilde x}_k}} \right\|}^2} + 3{{\left\| {{{\widetilde W}_k}} \right\|}^2}{{\left\| {\sigma ({{\widehat x}_k}){{\overline u }_k}} \right\|}^2} + 3{{\left\| {{{\bar \varepsilon }_{Ok}}} \right\|}^2}} \right] \le \\ \quad - (1 - {\gamma ^2}){\left\| {{{\widetilde x}_k}} \right\|^4} + {\left( {3{{\left\| {{{\widetilde W}_k}} \right\|}^2}{{\left\| {\sigma ({{\widehat x}_k}){{\overline u }_k}} \right\|}^2} + 3{{\left\| {{{\overline \varepsilon }_{Ok}}} \right\|}^2}} \right)^2} + \\ \quad 2\gamma {\left\| {{{\widetilde x}_k}} \right\|^2}\left( {3{{\left\| {{{\widetilde W}_k}} \right\|}^2}{{\left\| {\sigma ({{\widehat x}_k}){{\overline u }_k}} \right\|}^2} + 3{{\left\| {{{\overline \varepsilon }_{Ok}}} \right\|}^2}} \right) \le \\ \quad - (1 - 2{\gamma ^2}){\left\| {{{\widetilde x}_k}} \right\|^4} + 36{\left\| {{{\widetilde W}_k}} \right\|^4}{\left\| {\sigma ({{\widehat x}_k}){{\overline u }_k}} \right\|^4} + 36{\left\| {{{\overline \varepsilon }_{Ok}}} \right\|^4}. \end{array} $ | (A11) |
Next,take $L({\tilde{ {W}}}_k )$. Recall (A4) and write the difference $L({\tilde{ {W}}}_k )$ as
| $ \begin{align} & \Delta L({\tilde{ {W}}}_k )=({\rm tr}\{{\tilde{ {W}}}_{k+1}^{\rm T} {{ \Lambda \tilde {W}}}_{k+1} \})^2-({\rm tr}\{{\tilde{ {W}}}_k^{\rm T} {{ \Lambda \tilde {W}}}_k \})^2 \le\notag\\ & \quad \{-(1-2(1-\alpha _{I} )^2)\delta \left\| {{\tilde{ {W}}}_k } \right\|^2-\notag\\ & \quad2\beta _{I} \eta \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{\tilde{ {W}}}_k } \right\|^2 +\notag\\ & \quad6\beta _{I}^2 \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{{ A}}_c } \right\|^2\left\| {{{ lC}}} \right\|^2\left\| {{\tilde{ {x}}}_k } \right\|^2+\varepsilon _{{WM}} \}\times \notag\\ & \quad\{(1-2(1-\alpha _{I} )^2)\delta \left\| {{\tilde{ {W}}}_k } \right\|^2-2\beta _{I} \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{\tilde{ {W}}}_k } \right\|^2 +\notag\\ & \quad6\beta _{I}^2 \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{{ A}}_c } \right\|^2\left\| {{{ lC}}} \right\|^2\left\| {{\tilde{ {x}}}_k } \right\|^2+\varepsilon _{{WM}} \}\le \notag\\ & \quad \{-(1-2(1-\alpha _{I} )^2)\delta \left\| {{\tilde{ {W}}}_k } \right\|^2-\notag\\ & \quad2\beta _{I} \eta \delta \left\| {\sigma ({ \hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{\tilde{ {W}}}_k } \right\|^2+ \notag\\ & \quad6\beta _{I}^2 \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{{ A}}_c } \right\|^2\left\| {{{ lC}}} \right\|^2\left\| {{\tilde{ {x}}}_k } \right\|^2+\varepsilon _{{WM}} \}\times \notag\\ & \quad\{(1-2(1-\alpha _{I} )^2)\delta \left\| {{\tilde{ {W}}}_k } \right\|^2-\notag\\ & \quad2\beta _{I}\delta\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{\tilde{ {W}}}_k } \right\|^2 +\notag\\ & \quad6\beta _{I}^2 \delta\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2\left\| {{{ A}}_c } \right\|^2\left\| {{{ lC}}} \right\|^2\left\| {{\tilde{ {x}}}_k } \right\|^2+\varepsilon _{{WM}} \}\le \notag\\ & \quad -(1-8(1-\alpha _{I} )^4)\delta ^2\left\| {{\tilde{ {W}}}_k } \right\|^4+5\varepsilon _{{WM}}^2 -\notag\\ & \quad8(1-\alpha _{I} )^2\beta _{I} \eta \delta \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{\tilde{ {W}}}_k } \right\|^2+ \notag\\ & \quad { }210\beta _{I}^2 \delta ^2\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{ { A}}_c } \right\|^4\left\| {{{ lC}}} \right\|^4\left\| {{\tilde{ {x}}}_k } \right\|^4+ \notag\\ & \quad { }12\beta _{I}^2 \eta ^2\delta ^2\left\| {\sigma ({ \hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^8\left\| {{\tilde{ {W}}}_k } \right\|^4\le \notag\\ & \quad -(1-8(1-\alpha _{I} )^4)\delta ^2\left\| {{\tilde{ {W}}}_k } \right\|^4 -\notag\\ & \quad4(2(1-\alpha _{I} )^2-3\eta )\beta _{I} \eta \delta^2\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{\tilde{ {W}}}_k } \right\|^4 +\notag\\ & \quad { }210\Lambda ^2\left\| {{{ A}}_c } \right\|^4\left\| {{{ lC}}} \right\|^4\left\| {{\tilde{ {x}}}_k } \right\|^4+5\varepsilon _{{WM}}^2 , \end{align} $ | (A12) |
where $\eta =2(1-\alpha _{I} )\lambda _{\min } ({{ lC}})-\beta _{I} \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2$.
Therefore,combining (A11) and (A12) yields
| $ \begin{align} &\Delta L({\tilde{ {x}}}_k )+\Delta L({\tilde{ {W}}}_k ) \le-(1-2\gamma ^2)\left\| {{\tilde{ {x}}}_k } \right\|^4+\notag\\ & \quad 36\left\| {{\tilde{ {W}}}_k } \right\|^4\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4+36\left\| {{\bar{ {\varepsilon }}}_{Ok} } \right\|^4 -\notag\\ & \quad(1-8(1-\alpha _{I} )^4)\delta ^2\left\| {{\tilde{ {W}}}_k } \right\|^4 -\notag\\ & \quad4(2(1-\alpha _{I} )^2-3\eta )\beta _{I} \eta \delta ^2\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{\tilde{ {W}}}_k } \right\|^4 +\notag\\ & \quad52.5\Lambda ^2\gamma ^2\left\| {{{ A}}_c } \right\|^4\left\| {{{ lC}}} \right\|^4\left\| {{\tilde{ {x}}}_k } \right\|^4+5\varepsilon _{{WM}}^2 \le\notag\\ & \quad -(1-3\gamma ^2)\left\| {{\tilde{ {x}}}_k } \right\|^4-4\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{\tilde{ {W}}}_k } \right\|^4 { }-\notag\\ & \quad(1-8(1-\alpha _{I} )^4)\delta^2\left\| {{\tilde{ {W}}}_k } \right\|^4+\varepsilon _4 ,\end{align} $ | (A13) |
where $\varepsilon _4 =36\left\| {{\bar{ {\varepsilon }}}_{Ok} } \right\|^4+5\varepsilon _{{WM}}^2 $. Finally,combining (A10) and (A13) yields the first difference of the total Lyapunov candidate as
| $ \begin{align} &\Delta L_{{\tilde{ {W}}}_V } (k)=\Delta L({\tilde{ {W}}}_{Vk} )+\Pi \Delta L({\tilde{ {x}}}_k )+\Pi \Delta L({\tilde{ {W}}}_k ) \le\notag\\ & \quad -\frac{\alpha _V (1-6\alpha _V )}{2}\frac{\Delta \hat {\sigma }_{\min }^2 }{1+\Delta \hat {\sigma }_{\min }^2 }\left\| {{\tilde{ {W}}}_{Vk} } \right\|^2 -\notag\\ & \quad{ }\alpha _V (1-2\alpha _V )\frac{\hat {\sigma }_{\min }^2 }{1+\hat {\sigma }_{\min }^2 }\left\| {{\tilde{ {W}}}_{Vk} } \right\|^2 -\notag\\ & \quad { }\frac{\alpha _V (1+3\alpha _V )}{1+\Delta \hat {\sigma }_{\min }^2 }L_m^2 \left\| {{\tilde{ {x}}}_k } \right\|^4-4\Pi \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{\rm {\tilde { W}}}_k } \right\|^4 -\notag\\ & \quad { }(1-8(1-\alpha _{I} )^4)\Pi \delta ^2\left\| {{\tilde { {W}}}_k } \right\|^4+\varepsilon _1 ,\end{align} $ | (A14) |
where $\varepsilon _1 =\varepsilon _{V{TM}} +\Pi \varepsilon _4 $. By using standard Lyapunov stability analysis,$\Delta L$ is less than zero outside a compact set as long as the following conditions hold:
| $ \begin{align}\left\| {{\tilde{ {x}}}_k } \right\|>\sqrt[4]{\frac{\varepsilon _1 }{\frac{\alpha _V (1+3\alpha _V )}{1+\Delta \hat {\sigma }_{\min }^2 }L_m^2 }}\equiv b_{{\tilde{ {x}}}} ,\end{align} $ | (A15) |
or
| $ \begin{array}{*{20}{c}} {\left\| {{{\widetilde W}_{Vk}}} \right\| > \sqrt {\frac{{{\varepsilon _1}}}{{\frac{{{\alpha _V}(1 - 6{\alpha _V})}}{2}\frac{{\Delta {{\hat \sigma }_{{{\min }^2}}}}}{{1 + \Delta {{\hat \sigma }_{{{\min }^2}}}}} + {\alpha _V}(1 - 2{\alpha _V})\frac{{{{\hat \sigma }_{{{\min }^2}}}}}{{1 + {{\hat \sigma }_{{{\min }^2}}}}}}}} }\\ { \equiv {b_{{{\widetilde W}_V}}},} \end{array} $ | (A16) |
or
| $ \begin{align}\left\| {{\tilde{ {W}}}_k } \right\|>\sqrt[4]{\frac{\varepsilon _1 }{4\Pi \chi _{\min }^4 +(1-8(1-\alpha _{I} )^4)\Pi \delta ^2}}\equiv b_{{\tilde{ {W}}}} . \end{align} $ | (A17) |
Proof of Theorem 3. To show the convergence of the overall closed-loop system,we need to consider the entire design simultaneously (i.e.,the design of observer,critic NN and actor NN). We first show the convergence of the actor NN weight estimation error ${\tilde{ {W}}}_{{{ u}}k} $,then recalling from Theorems 1 and 2 with modifications, we will be able to show the boundedness of the overall closed-loop system.
Consider the following Lyapunov candidate:
| $ \begin{align}L(k)=L_{{IO}} (k)+L_{{\tilde{ {W}}}_V } (k)+\Sigma L_{{\tilde{ {W}}}_{{ u}} } (k),\end{align} $ | (A18) |
$L_{{IO}} (k)$ and $L_{{\tilde{ {W}}}_V } (k)$ are defined in (A1) and (A8),respectively,and $L_{{\tilde{ {W}}}_{{ u}} } (k)=\left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\|$ with
| $ \Sigma =\min \left\{ {\begin{array}{l} \frac{\alpha _V (1-2\alpha _V )\hat {\sigma }_{\min }^2 \bar {\varepsilon }_{{{ u}}{M}} }{\alpha _{{ u}} (5+4\bar {\varepsilon }_{{{ u}}{M}} )\nabla \sigma _{V\max }^2 \hat {\sigma }_{\min }^2 +2\bar {\varepsilon }_{{{ u}}{M}} },\\ \frac{(1-2(1-\alpha _{I} )^2)\Lambda (1+\hat {\sigma }_{\min }^2 )\bar {\varepsilon }_{{{ u}}{M}} }{2\alpha _{{ u}} \sigma _g^2 (1+\hat {\sigma }_{\min }^2 +\bar {\varepsilon }_{{{ u}}{M}} \lambda _{\max } ({{R}}^{-1}))} \\ \end{array}} \right\}. $ |
Denote $\hat {\sigma }_{{{ u}}k} =\sigma _{{ u}} ({\hat{ {x}}}_k ,k)$,${{ g}}_k^{\rm T} =g^{\rm T}({{ x}}_k )$,${\hat{ {g}}}_k^{\rm T} =g^{\rm T}({\hat{ {x}}}_k )$ and ${\tilde{ {g}}}_k^{\rm T} =\tilde {g}^{\rm T}({\hat{ {x}}}_k )$ for simplicity,then recalling (32) and (33),the first difference of $L_{{\tilde{ {W}}}_{{ u}} } (k)$ is given by
| $ \Delta L_{{\tilde{ {W}}}_{{ u}} } (k)=\left\| {{\tilde{ {W}}}_{{{ u}}k+1} } \right\|-\left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\|=\\\quad\left\| {{\tilde{ {W}}}_{{{ u}}k} +\alpha _{{ u}} \frac{\hat {\sigma }_{{{ u}}k} {{ e}}_{{{ u}}k}^{\rm T} }{1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} }} \right\|-\left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\| \le \\~~ \left\| {\begin{array}{*{20}l} \\ {\tilde{ {W}}}_{{{ u}}k} -\alpha _{{ u}} \frac{\hat {\sigma }_{{{ u}}k} \hat {\sigma }_{{{ u}}k}^{\rm T} {\tilde { {W}}}_{{{ u}}k} }{1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} }-\alpha _{{ u}} \frac{\hat {\sigma }_{{{ u}}k} {{R}}^{-1}{{ g}}_k^{\rm T} \nabla \hat {\sigma }_{Vk+1}^{\rm T} {\tilde{ {W}}}_{Vk} }{2(1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} )} -\\ \quad\alpha _{{ u}} \frac{\hat {\sigma }_{{{ u}}k} {{R}}^{-1}{\tilde{ {g}}}_k^{\rm T} \nabla \hat {\sigma }_{Vk+1}^{\rm T} {{W}}_V }{2(1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} )} -\\ \quad\alpha _{{ u}} \frac{\hat {\sigma }_{{{ u}}k} {{ R}}^{-1}\left( {{\hat{ {g}}}_k^{\rm T} -{{ g}}_k^{\rm T} } \right)\nabla \hat {\sigma }_{Vk+1}^{\rm T} {\tilde{ {W}}}_{Vk} }{2(1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} )}+ \\ \quad \alpha _{{ u}} \frac{\hat {\sigma }_{{{ u}}k} {{R}}^{-1}{\tilde{ {g}}}_k^{\rm T} \nabla \hat {\sigma }_{Vk+1}^{\rm T} {\tilde{ {W}}}_{Vk} }{2(1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} )}+\alpha _{{ u}} \frac{\hat {\sigma }_{{{ u}}k} {\bar{ {\varepsilon }}}_{{{ u}}k}^{\rm T} }{1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{u}}k} } \\ \end{array}} \right\| -\\ \quad\left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\| \le\\ \quad \left( {1-\alpha _{{ u}} \frac{\hat {\sigma }_{{{ u}}\min }^2 }{1+\hat {\sigma }_{{{ u}}\min }^2 }} \right)\left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\|+\alpha _{{ u}} \left\| {\frac{{{R}}^{-2}g_{M}^2 \hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} {\bar{ {\varepsilon }}}_{{{ u}}k}^{\rm T} }{4(1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} )^2}} \right\| +\\ \quad\alpha _{{ u}} \left( {1+\frac{5}{4\left\| {{\bar{ {\varepsilon }}}_{{{ u}}k} } \right\|}} \right)\left\| {\nabla \hat {\sigma }_{Vk+1}^{\rm T} {\tilde{ {W}}}_{Vk} } \right\|^2+\frac{\alpha _{{ u}} \sigma _g^2 }{4\left\| {{\bar{ {\varepsilon }}}_{{{ u}}k} } \right\|}\left\| {{\tilde{ {W}}}_k } \right\|^2+ \\ \quad\alpha _{{ u}} \left\| {\frac{{{R}}^{-2}\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} \nabla \hat {\sigma }_{Vk+1}^{\rm T} \nabla \hat {\sigma }_{Vk+1} W_{{VM}}^2 \bar {\varepsilon }_{{{ u}}{M}} }{4(1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} )^2}} \right\|+ \\ \quad\alpha _{{ u}} \left\| {\frac{\hat {\sigma }_{{ { u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} {{ R}}^{-2}g_{M}^2 \bar {\varepsilon }_{{{ u}}{M}} }{(1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{ { u}}k} )^2}} \right\|+\\ \quad\alpha _{{ u}} \left\| {\frac{\hat {\sigma }_{{ { u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} {{ R}}^{-2}}{4(1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} )^2}} \right\|\sigma _g^2 \left\| {\tilde{ { {W}}}_k } \right\|^2+\\ \quad\alpha _{{ u}} \left\| {\frac{\hat {\sigma }_{{ { u}}k} {\bar{ {\varepsilon }}}_{{{ u}}k}^{\rm T} }{1+\hat {\sigma }_{{{ u}}k}^{\rm T} \hat {\sigma }_{{{ u}}k} }} \right\|-\left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\|\le \\ \quad -\alpha _{{ u}} \frac{\hat {\sigma }_{{{ u}}\min }^2 }{1+\hat {\sigma }_{{{ u}}\min }^2 }\left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\|+\\\quad\alpha _{{ u}} \left( {1+\frac{5}{4\left\| {{\bar{ {\varepsilon }}}_{{ { u}}k} } \right\|}} \right)\nabla \sigma _{V\max }^2 \left\| {{\tilde{ {W}}}_{Vk} } \right\|^2+ \\ \quad\alpha _{{ u}} \sigma _g^2 \left( {\frac{1}{4\left\| {{\bar{ {\varepsilon }}}_{{{ u}}k} } \right\|}+\frac{\lambda _{\max } ({{ R}}^{-1})}{4(1+\sigma _{{{ u}}\min }^2 )}} \right)\left\| {{\tilde{ {W}}}_k } \right\|^2+\bar {\varepsilon }_{T{M}} , $ | (A19) |
where $\bar {\varepsilon }_{T{M}} \!=\!\alpha _{{ u}} \left( \!\!{\begin{array}{c} \frac{5\lambda _{\max } ({{R}}^{-2})g_{M}^2 }{4(1+\sigma _{{{ u}}\min }^2 )} \\ +\frac{\lambda _{\max } ({{R}}^{-2})\nabla \sigma _{V\max }^2 W_{{VM}}^2 }{4(1+\sigma _{{{ u}}\min }^2 )}+\frac{\sigma _{{ { u}}\max } }{1+\sigma _{{{ u}}\min }^2 } \\ \end{array}} \!\!\right)\cdot$ $\bar {\varepsilon }_{{{ u}}{M}} $, $0 < \sigma _{{{ u}}\min } < \left\| {\hat {\sigma }_{{{ u}}k} } \right\| < \sigma _{{{ u}}\max } $ and $\left\| {\nabla \hat {\sigma }_{Vk+1}^{\rm T} } \right\|\le \nabla \sigma _{V\max } $.
Combine (A5),(A14) and (A19) to obtain the first difference of the total Lyapunov candidate as
| $ \Delta L(k)=\Delta L_{{IO}} (k)+\Delta L_{{\tilde{ {W}}}_V } (k)+\Delta \Sigma L_{{\tilde{ {W}}}_{{ u}} } (k) \le\\ \quad -(1-(1+4\gamma \left\| {{{ lC}}} \right\|^2)(1+\chi _{\min }^2 )\gamma )\left\| {{\tilde{ {x}}}_k } \right\|^2+\varepsilon _{{OM}} -\\\quad \left\| {{\tilde{ {W}}}_k } \right\|^2\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2-(1-2(1-\alpha _{I} )^2)\delta \left\| {{\tilde{ {W}}}_k } \right\|^2 +\\ \quad { }\frac{\alpha _V (1-6\alpha _V )}{2}\frac{\Delta \hat {\sigma }_{\min }^2 }{1+\Delta \hat {\sigma }_{\min }^2 }\left\| {{\tilde{ {W}}}_{Vk} } \right\|^2 -\\ \quad\alpha _V (1-2\alpha _V )\frac{\hat {\sigma }_{\min }^2 }{1+\hat {\sigma }_{\min }^2 }\left\| {{\tilde{ {W}}}_{Vk} } \right\|^2 -\\ \quad\frac{\alpha _V (1+3\alpha _V )}{1+\Delta \hat {\sigma }_{\min }^2 }L_m^2 \left\| {{\tilde{ {x}}}_k } \right\|^4-4\Pi \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{ { \tilde { W}}}_k } \right\|^4- \\ \quad(1-8(1-\alpha _{I} )^4)\Pi \delta ^2\left\| {{\tilde{ {W}}}_k } \right\|^4+\varepsilon _1- \\ \quad\alpha _{{ u}} \Sigma \frac{\hat {\sigma }_{{{ u}}\min }^2 }{1+\hat {\sigma }_{{{ u}}\min }^2 }\left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\|+ \\ \quad\alpha _{{ u}} \Sigma \left( {1+\frac{5}{4\left\| {{\rm \bar {\varepsilon }}_{{{ u}}k} } \right\|}} \right)\nabla \sigma _{V\max }^2 \left\| {{\tilde{ {W}}}_{Vk} } \right\|^2 + \\ \quad\alpha _{{ u}} \Sigma \sigma _g^2 \left( {\frac{1}{4\left\| {{\bar{ {\varepsilon }}}_{{{ u}}k} } \right\|}+\frac{\lambda _{\max } ({{R}}^{-1})}{4(1+\sigma _{{{ u}}\min }^2 )}} \right)\left\| {{\tilde{ {W}}}_k } \right\|^2+\Sigma \bar {\varepsilon }_{T{M}}\le \\ \quad -\left( {1-(1+4\gamma \left\| {{{ lC}}} \right\|^2)(1+\chi _{\min }^2 )\gamma } \right)\left\| {{\tilde{ {x}}}_k } \right\|^2+\varepsilon _{{CLM}}- \\ \quad\left\| {{\tilde{ {W}}}_k } \right\|^2\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2-\frac{1}{2}(1-2(1-\alpha _{I} )^2)\delta \left\| {{\tilde{ {W}}}_k } \right\|^2- \\ \quad\frac{\alpha _V (1-6\alpha _V )}{2}\frac{\Delta \hat {\sigma }_{\min }^2 }{1+\Delta \hat {\sigma }_{\min }^2 }\left\| {{\tilde{ {W}}}_{Vk} } \right\|^2- \\ \quad\frac{\alpha _V (1-2\alpha _V )}{2}\frac{\Delta \hat {\sigma }_{\min }^2 }{1+\Delta \hat {\sigma }_{\min }^2 }\left\| {{\tilde{ {W}}}_{Vk} } \right\|^2 -\\ \quad 4\Pi \left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^4\left\| {{\tilde{ {W}}}_k } \right\|^4-\frac{\alpha _V (1+3\alpha _V )}{1+\Delta \hat {\sigma }_{\min }^2 }L_m^2 \left\| {{\tilde{ {x}}}_k } \right\|^4 -\\ \quad(1-8(1-\alpha _{I} )^4)\Pi \delta ^2\left\| {{\tilde{ {W}}}_k } \right\|^4-\alpha _{{ u}} \Sigma \frac{\hat {\sigma }_{{{ u}}\min }^2 }{1+\hat {\sigma }_{{{ u}}\min }^2 }\left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\|, $ |
where $\varepsilon _{{CLM}} =\varepsilon _{{OM}} +\varepsilon _1 +\Sigma \bar {\varepsilon }_{T{M}} $.
By using standard Lyapunov stability analysis,$\Delta L$ is less than zero outside a compact set as long as the following conditions hold:
| $ \begin{align} \left\| {{\tilde{ {x}}}_k } \right\|>\min \left\{ {\begin{array}{l} \sqrt {\frac{\varepsilon _{{CLM}} }{1-(1+4\gamma \left\| {{{lC}}} \right\|^2)(1+\chi _{\min }^2 )\gamma }} ,\\ \sqrt[4]{\frac{\varepsilon _{{CLM}} }{\frac{\alpha _V (1+3\alpha _V )}{1+\Delta \hat {\sigma }_{\min }^2 }L_m^2 }} \\ \end{array}} \right\}\equiv b_{{\tilde{ {x}}}} , \end{align} $ | (A20) |
or
| $ \left\| {{\tilde{ {W}}}_{Vk} } \right\|>\sqrt {\frac{\varepsilon _{{CLM}} }{\frac{\alpha _V (1-6\alpha _V )}{2}\frac{\Delta \hat {\sigma }_{\min }^2 }{1+\Delta \hat {\sigma }_{\min }^2 }+\alpha _V (1-2\alpha _V )\frac{\hat {\sigma }_{\min }^2 }{1+\hat {\sigma }_{\min }^2 }}} \\\equiv b_{{\tilde{ {W}}}_V } , $ | (A21) |
or
| $ \begin{align} \left\| {{\tilde{ {W}}}_k } \right\|>\min \left\{ {\begin{array}{l} \sqrt {\frac{\varepsilon _{{CLM}} }{\left\| {\sigma ({\hat{ {x}}}_k ){\bar{ {u}}}_k } \right\|^2+\frac{1}{2}(1-2(1-\alpha _{I} )^2)\delta }} ,\\ \sqrt[4]{\frac{\varepsilon _{{CLM}} }{4\Pi \chi _{\min }^4 +(1-8(1-\alpha _{I} )^4)\Pi \delta^2}} \\ \end{array}} \right\} { }\equiv b_{{\tilde{ {W}}}} ,\end{align} $ | (A22) |
or
| $ \begin{align} \left\| {{\tilde{ {W}}}_{{{ u}}k} } \right\|>\frac{\varepsilon _{{CLM}} }{\alpha _{{ u}} \Sigma \frac{\hat {\sigma }_{{{ u}}\min }^2 }{1+\hat {\sigma }_{{{ u}}\min }^2 }}\equiv b_{{\tilde{ {W}}}_{{ u}} } . \end{align} $ | (A23) |
Eventually,the difference between the inputs of the ideal optimal control and the proposed near optimal control inputs is represented as
| $ \begin{align} &\left\| {{{ u}}^\ast ({{ x}}_k ,k)-{\hat{ {u}}}({\hat{ {x}}}_k ,k)} \right\| =\notag\\ & \quad\left\| {{{W}}_{{ u}}^{\rm T} \sigma _{{ u}} ({{ x}}_k ,k)+\varepsilon _{{ u}} ({{ x}}_k ,k)-{\hat{ {W}}}_{{{ u}}k}^{\rm T} \sigma _{{ u}} ({\hat{ {x}}}_k ,k)} \right\| =\notag\\ & \quad\left\| {{\tilde{ {W}}}_{{{ u}}k}^{\rm T} \sigma _{{ u}} ({\hat{ {x}}}_k ,k)+{{ W}}_{{ u}}^{\rm T} \tilde {\sigma }_{{ u}} ({ { x}}_k ,{\hat{ {x}}}_k ,k)+\varepsilon _{{ u}} ({{ x}}_k ,k)} \right\| \le\notag\\ & \quad b_{{\tilde{ {W}}}_{{ u}} } \sigma _{{{ u}}{M}} +W_{{{ u}}{M}} \left\| {\tilde {\sigma }_{{ u}} ({{ x}}_k ,{\hat{ {x}}}_k ,k)} \right\|+\varepsilon _{{{ u}}{M}} \le\notag\\ & \quad b_{{\tilde{ {W}}}_{{ u}} } \sigma _{{{ u}}{M}} +l_\sigma W_{{{ u}}{M}} \left\| {{\tilde{ {x}}}_k } \right\|+\varepsilon _{{{ u}}{M}}\le \notag\\ & \quad b_{{\tilde{ {W}}}_{{ u}} } \sigma _{{{ u}}{M}} +l_\sigma W_{{{ u}}{M}} b_{{\tilde{ {x}}}} +\varepsilon _{{{ u}}{M}} =\varepsilon _{uo} , \end{align} $ | (A24) |
where $l_\sigma $ is the Lipschitz constant of $\sigma _{{ u}} (\cdot )$,and $b_{{\tilde{ {W}}}_{{ u}} },b_{{\tilde{ {x}}}} $ are given in (A23) and (A20),respectively.
| [1] | Kirk D. Optimal Control Theory: An Introduction. New Jersey: Prentice-Hall, 1970. |
| [2] | Lewis F L, Syrmos V L. Optimal Control (Second edition). New York:Wiley, 1995. |
| [3] | Bradtke S J, Ydstie B E, Barto A G. Adaptive linear quadratic controlusing policy iteration. In: Proceedings of the 1994 American ControlConference. Baltimore, MD, USA: IEEE, 1994. 3475-3479 |
| [4] | Abu-Khalaf M, Lewis F L. Nearly optimal control laws for nonlinearsystems with saturating actuators using a neural network HJB approach.Automatica, 2005, 41(5): 77-79 |
| [5] | Xu H, Jagannathan S, Lewis F L. Stochastic optimal control of unknownnetworked control systems in the presence of random delays and packetlosses. Automatica, 2012, 48(6): 1017-1030 |
| [6] | Xu H, Jagannathan S. Stochastic optimal controller design for uncertainnonlinear networked control system via neuro dynamic programming.IEEE Transactions on Neural Networks and Learning Systems, 2013,24(3): 471-484 |
| [7] | Dierks T, Jagannathan S. Online optimal control of affine nonlineardiscrete-time systems with unknown internal dynamics by using timebasedpolicy update. IEEE Transactions on Neural Networks and LearningSystems, 2012, 23(7): 1118-1129 |
| [8] | Chen Z, Jagannathan S. Generalized Hamilton-Jacobi-Bellman formulationbased neural network control of affine nonlinear discrete-timesystems. IEEE Transactions on Neural Networks, 2008, 19(1): 90-106 |
| [9] | Slotine J E, Li W. Applied Nonlinear Control. Englewood Cliffs, NJ:Prentice-Hall, 1991. |
| [10] | Khalil H K, Laurent P. High-gain observers in nonlinear feedbackcontrol. International Journal of Robust and Nonlinear Control, 2014,24(6): 993-1015 |
| [11] | Beard R. Improving the Closed-Loop Performance of Nonlinear Systems[Ph. D. dissertation], Rensselaer Polytechnic Institute, USA, 1995. |
| [12] | Cheng T, Lewis F L, Abu-Khalaf M. A neural network solution forfixed-final-time optimal control of nonlinear systems. Automatica, 2007,43(3): 482-490 |
| [13] | Heydari A, Balakrishan S N. Finite-horizon input-constrained nonlinearoptimal control using single network adaptive critics. IEEE Transactionson Neural Networks and Learning Systems, 2013, 24(1): 145-157 |
| [14] | Wang F Y, Jin N, Liu D R, Wei Q L. Adaptive dynamic programmingfor finite-horizon optimal control of discrete-time nonlinear systemswith ε-error bound. IEEE Transactions on Neural Networks, 2011, 22(1):24-36 |
| [15] | Al-Tamimi A, Lewis F L, Abu-Khalaf M. Discrete-time nonlinearHJB solution using approximate dynamic programming: convergenceproof. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetic, 2008, 38(4): 943-949 |
| [16] | Narendra K S, Parthasarathy K. Identification and control of dynamicalsystems using neural networks. IEEE Transactions on Neural Networks,1990, 1(1): 4-27 |
| [17] | Sarangapani J. Neural Network Control of Nonlinear Discrete-TimeSystems. Boca Raton, FL: CRC Press, 2006. |
| [18] | Yu W. Nonlinear system identification using discrete-time recurrentneural networks with stable learning algorithms. Information Sciences,2004, 158: 131-147 |
| [19] | Zhang X, Zhang H G, Sun Q Y, Luo Y H. Adaptive dynamic programmingbased optimal control of unknown nonaffine nonlinear discretetimesystems with proof of convergence. Neurocomputing, 2012, 91:48-55 |
| [20] | Vance J, Jagannathan S. Discrete-time neural network output feedbackcontrol of nonlinear discrete-time systems in non-strict form. Automatica,2008, 44(4): 1020-1027 |
| [21] | Si J, Barto A G, Powell W B, Wunsch D. Handbook of Learningand Approximate Dynamic Programming. Hoboken: Wiley-IEEE Press,2004. |
 2014, Vol.1
2014, Vol.1 


