Ⅰ. INTRODUCTION

THE problem of cooperative motion of mobile sensor vehicles along given curves have been widely investigated by the requirement of ocean sampling^{[1, 2]}. For the purpose of enhancing both the quantity and quality of collected information,the coordinated vehicle sea-routes are designed according to the spatial and temporal variability in the field. Therefore,a systematic method is urgently needed to deal with the coordinated path-following control problem for a given set of desired orbits.

Early works on the coordinated path-following design have focused on three popular methodologies,such as leader-following strategy^{[3, 4, 5, 6, 7, 8]},virtual structure^{[9, 10]} and decoupling approach^{[11, 12]}. As we all know,most existing results concentrate on Newton$'$s particles or wheeled robots and each design methodology has its weakness. In the leader-following strategy,group robustness is weak due to no information flow from the followers to the leaders. The formation in the virtual structure is rigid. The application of the decoupling approach requires an extra upgrade scheme to synchronize the parametrization states of given paths (e.g.,the parameter of each curve). In addition,when the decoupling approach is used to deal with fully actuated surface vessels,it is required to assume that the total linear speed of each vessel is nonzero all the time.

With the technological development of ocean sampling and the launching of scientific experiments^{[13, 14]},a novel geometric extension design has emerged in the coordinated path-following control recently and received much attention^{[15, 16, 17, 18]}. The main idea of this approach is to extend the given curve to be a family of level curves of an orbit function. Path-following is achieved through driving the value of the orbit function to the nominated value while formation motion along orbits is accomplished by forcing relative arc-lengths to the reference values. Zhang and his colleague first used this method to deal with unit-speed particles^[15] and then second-order particles^[16]. Chen and Tian^[17] extended this method to deal with the directed topology. To maintain the same geometric topology among the extended curves and the given curve,a new geometric extension design method named concentric compression^[18] was proposed to deal with the convex loops and then give a solution to unicycles. A similar idea was used to control simple 3D nonholonomic aircrafts^[19].

Since sensor measurements collected along repeated orbits with long,nearly straight sides could not use a complex environment model,the (near) optimal sampling trajectory for each sensor platform in ocean sampling was often designed as a convex and closed curve^[2]. In the event that some missions,such as the underway replenishment and the improvement of the underwater communication,request vessels in the desired attitude pattern^[12],we consider the navigation of formation motion of fully actuated surface vessels along a set of convex and closed orbits while maintaining attitude synchronization. The later control task (i.e.,attitude synchronization) was not involved in the mostly recent works^{[4, 5, 6, 7, 9, 11, 12, 15, 16, 17, 18, 19]}. One contribution of this paper is that we have found that some techniques developed for the coordinated path-following control of unicycles in earlier work^[18] can be applied to deal with fully actuated surface vessels by transforming the vessel$'$s model. These include the geometric extension design and formation based on consensus technique. It must be emphasized that we introduce the potential function that is usually applied in collision avoidance^[20] to ensure the condition of the model transformation (that is the requirement of the nonzero total linear speed of each surface vessel all the time),which is as an assumption in the literature^[12].

Compared with the existing works^{[11, 18, 19]},another distinct feature of the paper is that we remove the requirement that every vessel in the family demands to obtain the information of the reference orbital velocity,which is unreasonable in almost all environments. In this paper,the reference orbital velocity under consideration is a time-invariant signal. To solve the signal estimation,we develop the traditional adaptive control for one system to deal with the coordinated adaptation estimation by using the consensus technology. Such technical development is nontrivial because the control system turns into the multi-agent system and the estimated object is not the parameter of the vessel itself,which implies that we cannot only use the states of vessel itself to estimate the reference. Therefore,the neighbors$'$ information is used to construct the coordinated adaptation estimator,which makes our controller more scalable. The other difficulty is that the whole system is nonlinearly coupled and we cannot use the adaptive analysis method used in the multiple linear systems^{[21, 22]}. Thus the adaptive backstepping technology is adopted in this paper. In the literature,some researchers have considered adaptive formation control problems in the leader-following structure. Choi et al.^[4] used projection algorithm to estimate the leader$'$s velocity and the information used was the leader-following relative distance and bearing angle. Peng et al.^{[5, 6]} used neural network to compensate the uncertain leaders$'$ and followers$'$ parameters,respectively. This paper is different in that we combine the traditional adaptive method and consensus technique to construct the estimator,the link topology is not the leader-following structure and we only demand the communication topology to be connected and at least one vessel could get the information of the reference.

This paper is organized as follows. Section II formulates the coordinated control problem along orbits. In Section III,the cooperative control is designed according to the adaptive backstepping technology. Simulation results are presented in Section IV. Conclusion is given in Section V.

Ⅱ. PROBLEM STATEMENT A. Fully Actuated Surface Vessel$'$s Model

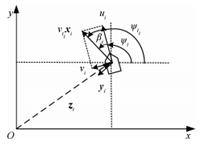
Consider a dynamic model,depicted in Fig. 1,whose actuators can be applied to surge,sway and yaw accelerations by using $\tau _{u_i }$,$\tau _{\upsilon _i }$ and $\tau _{r_i }$. The simplified dynamics of the $i$th fully actuated surface vessel in the inertial reference frame ${\bf W}$ are written as^[23]

\begin{align} \label{E1} \left\{ {\begin{array}{*{20}l} {\dot x_i = u_i \cos \psi _i-\upsilon _i \sin \psi _i } \\ {\dot y_i = u_i \sin \psi _i + \upsilon _i \cos \psi _i } \\ {\dot \psi _i = r_i } \\ {\dot u_i = \frac{1}{{m_{u_i } }}\left( {\tau _{u_i } + m_{\upsilon _i } \upsilon _i r_i-d_{u_i } u_i } \right)} \\ {\dot \upsilon _i = \frac{1}{{m_{\upsilon _i } }}\left( {\tau _{\upsilon _i }-m_{u_i } u_i r_i-d_{\upsilon _i } \upsilon _i } \right)} \\ {\dot r_i = \frac{1}{{m_{r_i } }}\left( {\tau _{r_i }-m_{u\upsilon _i } u_i \upsilon _i-d_{r_i } r_i } \right)} \\ \end{array}} \right. \end{align}

(1)

where ${\pmb z}_i= [x_i ,y_i]^{\rm T} $ is the position of the $i$th vessel,$\psi _i $ denotes its yaw angle,$u_{i}$, $\upsilon_{i}$ and $r_{i}$ are the surge,sway and yaw angle velocities,respectively,$m'$s and $d'$s are the parameters of surface vessel.

For the purpose of identifying the path-following errors in the next section,by referring [12] we define $\upsilon _{t_i } = \sqrt {u_i^2 + \upsilon _i^2 } $ to be the total line speed of surface vessel. By defining the sideslip angle as $\beta_{i} = \arctan \left( {\frac{{\upsilon _i }}{{u_i }}} \right)$,we regard $\psi _{t_i } = \psi _i + \beta _i $ as the total motion direction with respect to the $x$-axis of ${\bf W}$. Then the model of the fully actuated surface vessel in the flow frame $\mathbf{F}$ is rewritten as

\begin{align} \label{E2}\left\{ {\begin{array}{*{20}l} {\dot {\pmb z}_i = \upsilon _{t_i } {\pmb x}_i } \\ {\dot {\pmb x}_i = (r_i + \dot \beta _i ) {\pmb y}_i } \\ {\dot {\pmb y}_i =-(r_i + \dot \beta _i ){\pmb x}_i } \\ {\dot \upsilon _{t_i } = \tau _{t_i } + g_{t_i } } \\ {\dot \beta _i = \tau _{\beta _i } + g_{\beta _i } } \\ {\dot r_i = \frac{1}{{m_{r_i } }}\tau _{r_i } + g_{r_i } } \\ \end{array}} \right. \end{align}

(2)

where ${\pmb x}_i=\left[\cos\psi _{t_i },\sin\psi _{t_i }\right]^{\rm T}$ denotes the orientation of the $i$th vessel$'$s total motion,${\pmb y}_i=\left[-\sin\psi _{t_i },\cos\psi _{t_i }\right]^{\rm T}$ is the direction perpendicular to ${\pmb x}_i$,

\begin{align} \label{E3}\tau _{t_i } = \frac{{\cos \beta _i }}{{m_{u_i } }}\tau _{u_i } + \frac{{\sin \beta _i }}{{m_{\upsilon _i } }}\tau _{\upsilon _i } \end{align}

(3)

is the total line acceleration of the $i$th vessel,

\begin{align} \label{E4}\tau _{\beta _i } =-\frac{{\sin \beta _i }}{{\upsilon _{t_i } m_{u_i } }}\tau _{u_i } + \frac{{\cos \beta _i }}{{\upsilon _{t_i } m_{\upsilon _i } }}\tau _{\upsilon _i } \end{align}

(4)

is the total orientation angle acceleration of the $i$th vessel, the parameters $\{g_{t_i },g_{\beta _i },g_{r_i }\}$ are in the following forms: \begin{align*} &g_{t_i } = \left( \frac{{m_{\upsilon _i } }}{{m_{u_i } }}- \frac{{m_{u_i } }}{{m_{\upsilon _i } }}\right )\upsilon _{t_i } r_i \sin \beta _i \cos \beta _i-\\ & ~~~~ \left( \frac{{d_{u_i } }}{{m_{u_i } }}\cos ^2 \beta _i + \frac{{d_{\upsilon _i } }}{{m_{\upsilon _i } }}\sin ^2 \beta _i \right)\upsilon _{t_i }, \end{align*} \begin{align*} &g_{\beta _i } =-\frac{{m_{\upsilon _i } }}{{m_{u_i } }}r_i + \left( {\frac{{m_{\upsilon _i } }}{{m_{u_i } }}-\frac{{m_{u_i } }}{{m_{\upsilon _i } }}} \right)r_i \cos ^2 \beta _i+\\ &~~~~\left( {\frac{{d_{u_i } }}{{m_{u_i } }}-\frac{{d_{\upsilon _i } }}{{m_{\upsilon _i } }}} \right)\sin \beta _i \cos \beta _i, \end{align*} $$g_{r_i } =-\frac{{d_{r_i } }}{{m_{r_i } }} + \frac{{m_{u\upsilon _i } }}{{m_{r_i } }}\upsilon _{t_i }^2 \sin \beta _i \cos \beta _i.$$ From (3) and (4),the transformation between $(\tau _{u_i },\tau _{\upsilon _i })$ and $(\tau _{t_i },\tau _{\beta _i })$ is nonsingular if the total line speed $\upsilon_{t_i}$ is nonzero. In this paper,$u_{t_i}$ is designed to ensure that

\begin{align} \label{E5} \upsilon _{t_i }(t)>0 \end{align}

(5)

for $t\geq 0$,which is regarded as an assumption in [12]. For a simple statement,hereinafter we directly design $(\tau _{t_i },\tau _{\beta _i })$ to achieve the control object.

Remark 1. The inertia matrix,the matrix of coriolisand centripetal terms,and the damping matrix for the fully actuated surface vessel are usually not diagonal,but they also can be translated into the model in the flow frame which is similar to (2). To show the design process in a simple way,model (1) is used in this paper.

B. Concentric-compression-based Design

Consider the desired orbit $\mathcal {C}_{i0}$ for the $i$th surface vessel to be a simple,convex and closed curve with nonzero curvature. Similar to [18],we extend the given orbit $\mathcal {C}_{i0}$ by concentric compression,and then a family of level curves of an orbit function $f_i({\pmb z}_i)$ is constructed from the given orbit $\mathcal {C}_{i0}$. Furthermore, $f_i({\pmb z}_i)$ satisfies $\left| f_i({\pmb z}_i) \right| < \varepsilon _i~(\varepsilon _i> 0)$ and its gradient satisfies $\nabla f_i({\pmb z}_i)\ne 0,$ where symbol $\nabla$ denotes the vector differential operator. Each level curve corresponds to a special constant value of $f_i({\pmb z}_i)$,where the value of $f_i({\pmb z}_i)$ associated with the given orbit $\mathcal {C}_{i0}$ is $0$.

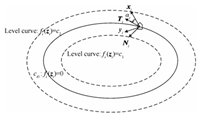
According to the extension of each given curve,one can obviously see that the path-following control should drive the orbit value $f_i \left( {{\pmb z}_i } \right)$ and the orientation difference $\alpha _i \in \left( {-\pi ,\pi } \right]$ between the vessel$'$s motion and the tangent vector $\pmb{T}_i$ to the orbit to $0$ asymptotically,and at the same time,ensure the trajectory of each vessel limited in set $\Omega_{i}$ (see Fig. 2),that is,

\begin{align} \label{E6} \lim _{t \to \infty } f_i ( {{\pmb z}_i \left( t \right)} ) = 0, \end{align}

(6)

\begin{align} \label{E7} \lim _{t \to \infty } \alpha _i ( t ) = 0, \end{align}

(7)

\begin{align} \label{E8} \left| {f_i \left( {{\pmb z}_i \left( t \right)} \right)} \right| < \varepsilon _i. \end{align}

(8)

For the simple representation,we use the brief symbol $f_i$ to represent $f_i \left( {{\pmb z}_i \left( t \right)} \right)$ hereinafter.

To coordinate vessels$'$ formation motion along the given orbits, the communication is essential. Let $\mathcal {G}=\{\mathcal{V},\mathcal{E}\}$ be the bidirectional graph induced by the inter-vessel communication topology,where $\mathcal{V}$ denotes the set of $n$ vessels and $\mathcal{E}$ is data links among vessels. Also let $\mathcal{N}_{i}$ and $\mathcal{L}$ denote the neighbor set of the $i$th vessel and the set of the vessels who have access to the time-invariant reference orbital velocity,respectively. Throughout the paper,we assume $\mathcal{N}_{i}$ and $\mathcal{L}$ are time-invariant. Two matrices,the adjacency matrix $A=[a_{ij}]$ and the Laplacian matrix $L=[l_{ij}]$,are used to represent the graph.

The key idea of formation motion around given orbits is based on the consensus design,which is widely applied in recent works^{[11, 12, 17, 18, 19]}. It is said that the formation pattern is maintained if all the generalized arc-lengths $\xi_{i}(t)$ defined in Assumption 1 reach consensus and their deviation $\eta_{i}(t)={\rm d}\xi_{i}/{\rm d} t$ converge to the constant reference $\eta^*>0$,i.e.,

\begin{align} \label{E9} \lim_{t\rightarrow \infty}\left(\xi_{i}(t)-\xi_{j}(t)\right)=0, \end{align}

(9)

\begin{align} \label{E10} \lim_{t\rightarrow \infty}\eta_{i}(t)=\eta^{*}. \end{align}

(10)

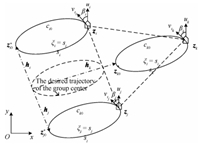
It must be noticed that $\eta_{i}(t)$ on the given orbit reflects the orbital velocity of vessel due to the fact that $\eta_{i}(t)$ defined in (20) is a product obtained by multiplying the velocity of vessel and a parameter with respect to the desired formation pattern. Therefore,$\eta_{i}(t)$ is regarded as the orbital velocity,and $\eta^*$ is called the time-invariant reference orbital velocity. For example,three vessels move along the given orbits obtained by translating the reference orbit along the formation vector $\pmb{h}_{i}$ while maintaining the rigid formation ${\pmb z}_{i}(t)-{\pmb z}_{j}(t)={\pmb h}_{i}-{\pmb h}_{j}$,as shown in Fig. 3. If we let the starting points $\pmb{z}_{i0}^*$ for computing the arc-lengths $s_i$ satisfy ${\pmb z}_{i}^*-{\pmb z}_{j}^*={\pmb h}_{i}-{\pmb h}_{j}$,it is required that $s_{i}(t)=s_{j}(t)$ to ensure the nominated formation. In the ocean exploration,the formation motion on the planar concentric curves often attracts attention,because ocean scales are usually similar through the upper water column^[2]. 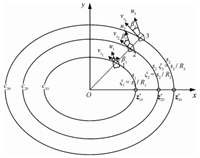Consider a simple example of coordinated path-following control along a set of concentric ellipses

\begin{align} \label{E11} {\left( {\frac{{x_i }}{a}} \right)^2 + \left( {\frac{{y_i }}{b}} \right)^2 = R_i^2 } \end{align}

(11)

with the different lengths of the semi-major and semi-minor axes given by $R_i a$ and $R_i b$. In Fig. 4,the in-line formation can be maintained if $\xi_{i}=s_{i}/R_i$ reach consensus where the starting point for each orbit is selected as the intersection of the orbit with the positive $x$-axis.

Assumption 1. $\xi_{i}$ is a $C^2$ smooth function of $s_i$ such that all ${\partial \xi _i }/{\partial s_i }$ are bounded,greater than $0$,and ${\partial ^2 \xi _i }/{\partial s_i^2 }$ are uniformly bounded for $i=1,\cdots,n$.

Some practical missions,such as underway replenishment and image acquisition^[12],require the attitude synchronization to improve the efficiency of system. In this paper,$\beta_{i}$ is regarded as the attitude of the $i$th ship,because variant $\beta_{i}$ with a constant linear speed causes variant sway-surge velocity combinations. It is said that the inter-vessel attitude reaches the relative desired attitude scalar $\beta_{i}^*\in\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$ (attitude synchronization) when

\begin{align} \label{E12}\lim_{t\rightarrow \infty}\left(\beta_{i}^{a}(t)-\beta_{j}^{a}(t)\right)=0, \end{align}

(12)

where $\beta_{i}^{a}=\beta_i-\beta_i^*$.

From the discussion above,the coordinated control problem along orbits is defined as follows.

Coordinated control problem along orbits: Based on local neighbor-to-neighbor information,design a path-following control for each vessel $$\tau_{r_i}\left({\pmb z}_i,{\pmb x}_{i},\upsilon_{t_i},\alpha_{i},f_i,s_i,\xi_i,\xi_j,\eta_i;i\in\mathcal{V},j\in\mathcal{N}_{i}\right),$$ the attitude synchronization controller $$\tau_{\beta_{i}}\left(\beta_{i},\beta_i^*,\beta_{j},\beta_j^*,\alpha_{i};i\in\mathcal{V},j\in\mathcal{N}_{i}\right),$$ and a formation control law \begin{align*} &\tau_{t_m}\left({\pmb z}_m,{\pmb x}_{m},\upsilon_{t_m},\alpha_{m},f_m,s_m,\xi_m,\xi_j,\eta_m,\eta_j,\eta_*;m\in\mathcal{L},\right.\\ &~~~~~~\left.j\in\mathcal{N}_{m}\right) \end{align*} for the vessel who has assess to the time-invariant reference orbital velocity,or \begin{align*} &\tau_{t_k}\left(\pmb{z}_k,\pmb{x}_{k},\upsilon_{t_k},\alpha_{k},f_k,s_k,\xi_k,\xi_j,\eta_k,\eta_j,\hat{\eta}_{k},\dot{\hat{\eta}}_{k};k\in{\mathcal{V}-\mathcal{L}},\right.\\ &~~~~~~\left.j\in\mathcal{N}_{k}\right) \end{align*} for the other vessels with the coordinated differential adaptation control $$\dot{\hat{\eta}}_{k}\left(\xi_k,\xi_j,\eta_k,\eta_j;k\in{\mathcal{V}-\mathcal{L}},j\in\mathcal{N}_{k}\right)$$ for $\eta^{*}$ such that requirements (5) $\sim$ (10) and (12) are satisfied.

Remark 2. The information required in the coordinated control law consists of two parts. On one hand,the states such as $\{{\pmb z}_i,u_i,\upsilon_i,\psi_i,r_i\}$ are measured in the inertial reference frame. Then we use them to calculate the states $\{{\pmb x}_i,{\pmb y}_i,\upsilon_{t_i},\beta_i,g_{t_i},g_{\beta_i},g_{r_i},\psi_{t_i}\}$ in the flow frame ${\bf F}_i$ and the values of $\{f_i,\nabla f_i,\nabla^2f_i,\nabla^3 f_i,\sin\alpha_i,\cos\alpha_i,s_i,\frac{\partial s_i}{\partial f_i},\frac{\partial^2 s_i}{\partial f_i^2},\xi_i,\frac{\partial \xi_i}{\partial s_i},\frac{\partial^2 \xi_i}{\partial s_i^2}$, $\eta_i,\beta_{i}^{a}\}$ according to the functional forms of $\{f_i,s_i,\xi_i,\eta_i,\beta_{i}^{a}\}$. The definition of each function can be found in Sections II-B and III-A. On the other hand, the information $\left\{\xi_i,\eta_i,\beta_{i}^{a}\right\}$ should be transferred to its neighbors for the coordinated path-following control and the coordinated adaptive control. The details can be found in Section III-B.

Ⅲ. MAIN RESULTS A. Coordinated Control Model

In set $\Omega_{i}$,due to the fact that the value of $f_i$ for the given orbit $\mathcal{C}_{i0} $ is $0$,the dynamics of position error of path-following is

\begin{align} \label{E13} \dot f_i = \nabla f_i \cdot \dot {\pmb{z}}_i = \nabla f_i \cdot \upsilon _{t_{i}} \pmb{x}_i. \end{align}

(13)

Let $\pmb{N}_i =-\frac{{\nabla f_i }} {{\left\| {\nabla f_i } \right\|}} $ and $\pmb{T}_i = \left[{\begin{array}{*{20}c} 0 & 1 \\ {-1} & 0 \\ \end{array} } \right]\pmb{N}_i$ be the normal vector and the tangent vector to each level curve,respectively. The orientation difference $\alpha _i$ between $\pmb{x}_i$ and $\pmb{T}_i$ can be defined as

\begin{align} \label{E14a} \cos \alpha _i = \pmb{x}_i \cdot \pmb{T}_i = \pmb{y}_i \cdot \pmb{N}_i , \end{align}

(14a)

\begin{align} \label{E14b} \sin \alpha _i = \pmb{y}_i \cdot \pmb{T}_i ~ =-\pmb{x}_i \cdot \pmb{N}_i. \end{align}

(14b)

Consequently,using (14a) we have

\begin{align} \label{E15} \dot f_i = \left\| {\nabla f_i } \right\|\upsilon _{t_{i}} \sin \alpha _i. \end{align}

(15)

Note that

\begin{align} \label{E16} \dot {\pmb {N}}_i =-\frac{{\upsilon _{t_{i}} }} {{\left\| {\nabla f_i } \right\|}}\left( {\nabla ^2 f_i \pmb{x}_i -\left( {\pmb{N}_i \cdot \nabla ^2 f_i \pmb{x}_i } \right)\pmb{N}_i } \right), \end{align}

(16)

where $\nabla ^2 f_i$ is the Hessian matrix of $f_{i}$. The time-derivative of equation (14b) along (2) and (16) yields

\begin{align} \label{E17} &\dot \alpha _i \cos \alpha _i =-\left(r_{i}+g_{\beta_{i}}+\tau_{\beta_{i}}\right)\cos \alpha _i+ \nonumber\\ &\quad \frac{{\upsilon _{t_{i}} }} {{\left\| {\nabla f_i } \right\|}}\left( {\pmb{x}_i \cdot \nabla ^2 f_i \pmb{x}_i + \left( {\pmb{N}_i \cdot \nabla ^2 f_i \pmb{x}_i } \right)\sin \alpha _i } \right). \end{align}

(17)

Considering that $\pmb{x}_i = \pmb{T}_i \cos \alpha _i- \pmb{N}_i \sin \alpha _i$,the direction error model is

\begin{align} \label{E18} \dot \alpha _i = \upsilon _{t_{i}} \left( {k_{a_i} \cos \alpha _i + k_{b_i} \sin \alpha _i } \right) -\left(r_{i}+g_{\beta_{i}}+\tau_{\beta_{i}}\right), \end{align}

(18)

where $$k_{a_i} = \frac{1}{{\left\| {\nabla f_i } \right\|}}\pmb T_i \cdot \nabla ^2 f_i \pmb T_i ,$$ $$k_{b_i} =-\frac{1}{{\left\| {\nabla f_i } \right\|}}\pmb T_i \cdot \nabla ^2 f_i \pmb N_i. $$

To compute the total variation of the arc-length,we use $\phi _i$ to reparametrize all the level curves in $\Omega_{i}$ in this paper. Once the starting point $\pmb{z}_{i0}^{\ast}$ of $\mathcal {C}_{i0}$ is decided,the starting point of each level curve is chosen such that its corresponding value of the parameter of the curve is the same as the value associated with $\pmb{z}_{i0}^{\ast}$ (i.e.,$ \phi _{i}^*$). Due to the fact that the change of arc-length $s_{i}$ is caused not only by the motion of the $i$th vessel projected to $\pmb{T}_i$ but also by the motion projected to the direction of concentric compression which changes the level curve,the arc-length $s_{i}$ between $\pmb{z}_{i}$ and the starting point of the orbit which $\pmb{z}_{i}$ belongs to is a function $s_i \left( {f_{i},\phi_{i} } \right)$. Furthermore,we can write $$ s_i \left( {f_i ,\phi _i } \right) := \int_{\phi _i^* }^{\phi _i } {\frac{{\partial s_i \left( {f_i ,\tau } \right)}} {{\partial \tau }}}\rm{d}\tau.$$

Remark 3. Consider the parametrized level (skewed) superellipses (including circles,ellipses,and rounded parallelograms) of the orbit function as \begin{align*} & \pmb{C} \left( {f_i,\phi _i } \right)\!=\! \left( {1-f_i } \right)\left[{ {a\left( {\cos \phi _i } \right)^{\frac{1} {p}} \!+\! \mu b\left( {\sin \phi _i } \right)^{\frac{1} {p}} }, b\left( {\sin \phi _i } \right)^{\frac{1} {p}} } \right]^{\rm{T}}, \end{align*} where $\mu$ is the skew parameter,the semi-major axis length $a$ and semi-minor axis length $b$ satisfy $a\geq b > 0$ and the parameter $p~(p=1,3,5,\cdots)$ determines the corner sharpness. For $\mu=0$ and $a>b$ (resp. $a$ = $b$),setting $p=1$ yields an ellipse (resp. circle) and setting $p\geq 3$ yields a rounded rectangle (resp. rounded square). Setting $\mu\neq0$ and $p>1$ yields a rounded parallelogram. The arc-length $s_i(f_i,\phi _i)$ measured from the starting points (corresponding to the parameter $\phi _i^\ast$) is \begin{align*} &{s_i}({f_i},{\phi _i}) = \left( {1-{f_i}} \right)\int_{\phi _i^*}^{{\phi _i}} \left[\left(-\frac{a}{p}\sin {\tau}{{\left( {\cos {\tau}} \right)}^{\frac{{1-p}}{p}}} + \right. \right. \\ &\quad\left.\left. \frac{{\mu b}}{p}\cos {\tau}{{\left( {\sin {\tau}} \right)}^{\frac{{1-p}}{p}}} \right)^2 + {{\left( {\frac{b}{p}\cos {\tau}{{\left( {\sin {\tau}} \right)}^{\frac{{1- p}}{p}}}} \right)}^2} \right]^{\frac{1}{2}}{\rm{d}}\tau. \end{align*} When each vessel moves,the dynamics of $s_i$ is \begin{align*} \label{E23} &\dot s_i = \frac{{\partial s_i }} {{\partial \phi _i }}\dot \phi_i + \frac{{\partial s_i }} {{\partial f_i }}\dot f_i = \\ &~~~~\frac{{{\rm d} s_i }} {{{\rm d}t}}\left| {_{\pmb{z}_i = \rm const} } \right. + \frac{{\partial s_i }} {{\partial f_i }}\left\| {\nabla f_i } \right\|\upsilon _{t_i} \sin \alpha _i=\\ &~~~~ \dot {\pmb{z}}_i \cdot \pmb{T}_i + \frac{{\partial s_i }} {{\partial f_i }}\left\| {\nabla f_i } \right\|\upsilon _{t_i} \sin \alpha _i=\\ & ~~~~ \upsilon _{t_i} \left( {\cos \alpha _i + \frac{{\partial s_i }} {{\partial f_i }}\left\| {\nabla f_i } \right\|\sin \alpha _i } \right). \end{align*} Then the total variation of generalized arc-length is

\begin{align} \dot \xi _i =\frac{\partial \xi _i }{\partial s_i}\dot{s}_i= \frac{{\partial \xi _i }} {{\partial s_i }}\upsilon _{t_i} \left( {\cos \alpha _i + \frac{{\partial s_i }} {{\partial f_i }}\left\| {\nabla f_i } \right\|\sin \alpha _i } \right). \end{align}

(19)

In the next subsection,we will design the path-following controller to drive each vessel to move along its given orbit, which implies $\dot \xi _i = \frac{{\partial \xi _i }} {{\partial s_i }}\upsilon _{t_i}$ as $\alpha_{i}=0$. Therefore,the orbital velocity $\eta_{i}$ is defined as

\begin{align} \label{E20} \eta _i = \frac{{\partial \xi _i }} {{\partial s_i }}\upsilon _{t_i}. \end{align}

(20)

From (20),we rewrite $\dot{\xi}_i(t)$ as

\begin{align} \label{E21} \dot \xi _i = \eta _i +d_{\eta_i}, \end{align}

(21)

where $d_{\eta_i}=-2\eta _i \sin ^2 \left( {\frac{{\alpha _i }}{2}} \right) + \eta _i \frac{{\partial s_i }}{{\partial f _i }}\left\| {\nabla f _i } \right\|\sin {\alpha _i } $. Taking the time derivative of $\eta_{i}$,we have

\begin{align} \label{E22} \dot \eta _i = \frac{{\partial \xi _i }} {{\partial s_i }}\left(g_{t_{i}}+\tau_{t_{i}}\right) + \frac{{\partial ^2 \xi _i }} {{\partial s_i^2 }}\upsilon _{t_i}^2 \left( {\cos \alpha _i + \frac{{\partial s_i }} {{\partial f_i }}\left\| {\nabla f_i } \right\|\sin \alpha _i } \right). \end{align}

(22)

Since $\beta_{i}$ is regarded as the attitude of the $i$th vessel, the dynamics of $\beta_{i}^{\alpha}$ is

\begin{align} \dot {\beta}_{i}^{\alpha} = g_{\beta_{i}} + \tau_{\beta_{i}} . \end{align}

(23)

To sum up,the coordinated control model for each vessel is summarized as follows:

\begin{align} \label{E24a} \dot f_i = \left\| {\nabla f_i } \right\|\upsilon _{t_i} \sin \alpha _i, \end{align}

(24a)

\begin{align} \label{E24b} \dot \alpha _i = \upsilon _{t_i} \left( {k_{a_i} \cos \alpha _i + k_{b_i} \sin \alpha _i } \right)- \left(r_{i}+g_{\beta_{i}}+\tau_{\beta_{i}}\right), \end{align}

(24b)

\begin{align} \label{E24c} \dot \xi _i = \eta _i +d_{\eta_i}, \end{align}

(24c)

\begin{align} \label{E24d} \dot \eta _i = \frac{{\partial \xi _i }} {{\partial s_i }}\left(g_{t_{i}}+\tau_{t_{i}}\right) + \frac{{\partial ^2 \xi _i }} {{\partial s_i^2 }}\upsilon _{t_i}^2 \left( {\cos \alpha _i + \frac{{\partial s_i }} {{\partial f_i }}\left\| {\nabla f_i } \right\|\sin \alpha _i } \right), \end{align}

(24d)

\begin{align} \label{E24e} \dot {\beta}_{i}^{\alpha} = g_{\beta _i } + \tau _{\beta _i }. \end{align}

(24e)

B. Controller Design

Since only a portion of the vessels belonging to set $\mathcal {L}$ have access to the reference constant state $\eta^*$,an estimate $\hat{\eta}_k$ is used to replace $\eta^*$ when the $k$th vessel in set $\mathcal {V}-\mathcal {L}$. The parameter error $\varphi_k$ is defined as

\begin{align} \label{E25} \varphi_k=\eta^*-\hat{\eta}_k. \end{align}

(25)

In the following,we show the design process of the adaptive backstepping design.

Step 1. Convergence of $f_{i},~\alpha_{i},~\xi_{i}-\xi_{j},~\eta_{m}-\eta^*,~\eta_{k}-\hat{\eta}_k, ~\beta_{i}^{\alpha}-\beta_{j}^{\alpha},~\varphi_k$. We start with the following Lyapunov function:

\begin{align} \label{E26}& V_I = \sum_{i = 1}^n {\left( {h_i \left( {f_i } \right)-\ln \left( {\cos ^2 \frac{{\alpha _i }} {2}} \right) } \right)} + \nonumber \\ &\quad\frac{k_0} {4}\sum_{i = 1}^n { {\sum_{j = 1}^n {a_{ij} \left( {\xi _i-\xi _j } \right)^2 } } }+\frac{1} {4}\sum_{i = 1}^n { {\sum_{j = 1}^n {a_{ij} \left( {\beta_{i}^{\alpha}-\beta_{j}^{\alpha} } \right)^2} } }\nonumber+ \\ &\quad\sum_{m\in\mathcal {L}}\left( {\ln\left(\frac{{\eta}_{m}}{{\eta}^{*}}\right)+\frac{{\eta}^{*}}{{\eta}_{m}}-1}\right)\nonumber+ \\ &\quad\sum_{k\in\{\mathcal {V}-\mathcal {L}\}}\left( {\ln\left(\frac{{\eta}_{k}}{{\hat{\eta}}_k}\right)+\frac{{\hat{\eta}}_k}{{\eta}_{k}}-1}\right)+\frac{1}{2}\sum_{k\in\{\mathcal {V}-\mathcal {L}\}}\varphi_k^2, \end{align}

(26)

where $k_0>0$,and $h_i \left( {f_i } \right)$ is a $C^2$ smooth nonnegative function on $\left( {-\varepsilon _i ,\varepsilon _i } \right)$ and satisfies the following conditions.

Condition 1. $h_i \left( {f_i } \right) \to + \infty$ and $\nabla h_i =\partial h_i/\partial f_i \to-\infty$ as $f_i \to -\varepsilon _i$.

Condition 2. $h_i \left( {f_i } \right) \to + \infty$ and $\nabla h_i \to +\infty$ as $f_i \to \varepsilon _i$.

Condition 3. $h_i \left( {f_i } \right)=0$ if and only if $f_i=0$.

There are many functions that satisfy all the above properties of $h_i \left( {f_i } \right)$. One example is \begin{align*} &h_i \left( f_i\right) =\int_{f_i^*}^{f_i}\left[c_1\left(\frac{1} {{\varepsilon _i-\tau}}-\frac{1} {{\varepsilon _i + \tau}}\right)\right.+\\ & \qquad \left.c_2\left( \ln \left( {\varepsilon _i + \tau} \right)-\ln \left( {\varepsilon _i-\tau} \right)\right)\right]\text{d}\tau, \end{align*} where $f_i^*=f_i(\pmb{z}_i(0))\in \Omega_i$ and $c_1,c_2>0$.

The first term in (26) contributes to guiding each vessel to move to its given orbit and stay in $\Omega_i$ when it starts from $\Omega_i$. The second term forces the difference between the direction of each vessel$'$s motion and the tangent vector to the orbit to be $0$. The next two terms ensure the agreement of the generalized arc-lengths and harmonize the relative attitude. The fifth term guarantees that $\eta_m$ converges to the reference state $\eta^*$ and $\upsilon_{t_m}=\left(\frac{\partial \xi_m}{\partial s_m}\right)^{-1}\eta_m(t)\neq 0$ all the time, where $m\in\mathcal {L}$. The last two terms have the same effect as the fifth term with estimate $\hat{\eta}^*_k$ approaching to ${\eta}^*$ when $k\in\{\mathcal {V}-\mathcal {L}\}$.

Note that $\dot{\varphi}_k=-\dot{\hat{\eta}}_k$,then the time derivation of $V_{I}$ is

\begin{align} \label{E27} \dot V_I & = \sum_{i=1}^{n} \tan\frac{\alpha _i }{2}\left( {\Delta _{r_i }-r_i } \right)+\sum_{i = 1}^n \Delta _{\beta _i}\left( {g_{\beta _i } + \tau _{\beta _i } } \right) \nonumber +\\ &\sum_{m\in\mathcal {L}} \left( \eta _m-{\eta}^{*} \right)\left( {\Delta _{\tau _{tm} } + \frac{1}{{\eta _m^2 }}\frac{{\partial \xi _m }}{{\partial s_m }}\left(\tau _{t_m }+g_{t_m}\right) } \right) \nonumber+ \\ & \sum_{k\in\{\mathcal {V}-\mathcal {L}\}} \left( {\eta _k-{\hat{\eta}}_k } \right)\left( \Delta _{\tau _{tk} }+\frac{1}{{\eta _k^2 }}\frac{{\partial \xi _k }}{{\partial s_k }}\left(\tau _{t_k }+g_{t_k}\right) \right)\nonumber-\\ &\sum_{k\in\{\mathcal {V}-\mathcal {L}\}}{\varphi}_k\left( {\dot{\hat{\eta}}}_k+k_0\sum_{j=1}^{n}a_{kj}(\xi_k-\xi_j)\right), \end{align}

(27)

where

\begin{align} \label{E28} &\Delta _{r_i } = \upsilon _{t_i } \left( k_{a_i} \cos \alpha _i + k_{b_i} \sin \alpha _i + 2\nabla h_i \left\| {\nabla f_i } \right\|\cos ^2 \frac{\alpha _i }{2}\right) \nonumber +\\ &\quad k_0 {\eta}_i \left( {-\sin \alpha _i + 2\frac{{\partial s_i }}{{\partial f_i }}\left\| {\nabla f_i } \right\|\cos ^2 \frac{{\alpha _i }}{2}} \right)\sum_{j = 1}^n {a_{ij} \left( {\xi _i-\xi _j } \right)}, \end{align}

(28)

\begin{align} \label{E29} \Delta _{\beta _i}= \sum_{j = 1}^n {a_{ij}\left( \beta _{i}^{\alpha}-\beta_{j}^{\alpha}\right)-\tan \frac{\alpha _i }{2} }, \end{align}

(29)

\begin{align} \label{E30} &\Delta _{\tau _{tm} } = \frac{{\partial ^2 \xi _m }}{{\partial s_m^2 }}\frac{{\upsilon _{t_m }^2 }}{{\eta _m^2 }} \left( {\cos \alpha _m + \frac{{\partial s_m }}{{\partial f_m }}\left\| {\nabla f_m } \right\|\sin \alpha _m } \right)\nonumber+ \\ &\quad k_0\sum_{j = 1}^n a_{mj} \left( {\xi _m-\xi _j } \right), \end{align}

(30)

\begin{align} \label{E31} &\Delta _{\tau _{tk} } = \frac{{\partial ^2 \xi _k }}{{\partial s_k^2 }}\frac{{\upsilon _{t_k }^2 }}{{\eta _k^2 }} \left( {\cos \alpha _k + \frac{{\partial s_k }}{{\partial f_k }}\left\| {\nabla f_k } \right\|\sin \alpha _k } \right)\nonumber+ \\ &\quad k_0\sum_{j = 1}^n a_{kj} \left( {\xi _k-\xi _j } \right)-\frac{\dot{\hat{\eta}}_k}{\eta_k\hat{\eta}_k}. \end{align}

(31)

Firstly,$r_{i}$ is regarded as a virtual control $\bar{r}_{i}$ and combined with $\tau _{t _i }$ and $\tau _{\beta _i }$ together for the purpose of making $\dot V_I\leq 0$. Let the virtual path-following control be

\begin{align} \label{E32} \bar r_i = \Delta _{r_i } + k_1 \sin \frac{{\alpha _i }}{2}, \end{align}

(32)

the attitude synchronization control be

\begin{align} \label{E33} \tau _{\beta _i } =-g_{\beta _i }-k_2 \Delta _{\beta _i}, \end{align}

(33)

and the formation control law be

\begin{align} \label{E34} &\tau _{t_m } =-g_{t_m }-\eta _m^2 \left( {\frac{{\partial \xi _m }}{{\partial s_m }}} \right)^{-1} \left( \Delta _{\tau _{tm} } + k_3 \left( {\eta _m-{\eta} ^{*} } \right)\right. \nonumber +\\ &\quad \left. k_4\sum_{j=1}^n a_{mj}\left(\eta_m-\eta_j\right) \right). \end{align}

(34)

If the $m$th vessel has access to the reference $\eta^*$,and

\begin{align} \label{E35} &\tau _{t_k } =-g_{t_k }-\eta_k^2 \left( {\frac{{\partial \xi _k }}{{\partial s_k }}} \right)^{-1} \left( \Delta _{\tau _{tk} } + k_3 \left( {\eta _k-{\hat{\eta}}_k } \right)\right. \nonumber+ \\ &\quad \left. k_4\sum_{j=1}^n a_{kj}\left(\eta_k-\eta_j\right)\right), \end{align}

(35)

for $k\in\{\mathcal {V}-\mathcal {L}\}$,where $k_{1},~k_{2},~k_{3},~k_4$ are some positive constants. Substituting (32) $\sim$ (35) into (27) results in

\begin{align} \label{E36} \dot V_I & =-k_1 \sum\limits_{i = 1}^n {\frac{{\sin ^2 \frac{{\alpha _i }}{2}}}{{\cos \frac{{\alpha _i }}{2}}}}-k_2 \sum\limits_{i = 1}^n \Delta _{\beta _i} ^2-k_3 \sum\limits_{m \in\mathcal {L}} {\left( {\eta _m-\eta ^* } \right)^2 } \nonumber-\\ & k_3 \sum\limits_{k \in \left\{ {\mathcal {V}-\mathcal {L}} \right\}}^n {\left( {\eta _k-\hat \eta _k } \right)^2 }-k_4 (\pmb{\eta}-\eta^*\pmb{1}_n)^{\rm T} L(\pmb{\eta}-\eta^*\pmb{1}_n)-\nonumber\\ & \sum\limits_{k \in \left\{ {\mathcal {V}-\mathcal {L}} \right\}} {\varphi_k \left( \dot {\hat{ \eta}} _k +\Delta_{\varphi_k} \right)}, \end{align}

(36)

where $\pmb{\eta}=\left[\eta_1,\cdots,\eta_n\right]^{\rm T}$,${\pmb 1}_n=[1,\cdots,1]^{\rm T}$,and

\begin{align} \label{E37}\Delta_{\varphi_k}=k_0 \sum_{j=1}^{n}a_{kj}(\xi_k-\xi_j)+k_4 \sum\limits_{j = 1}^n a_{kj} \left( {\eta _k-\eta _j } \right). \end{align}

(37)

With the appropriate choice of $\dot {\hat{ \eta}} _k$ we can discard the indefinite term $-\varphi_k\Delta_{\varphi_k}$. Thus the adaptive update law is

\begin{align} \label{E38} \dot {\hat{ \eta}} _k =-\Delta_{\varphi_k}, \end{align}

(38)

which yields $\dot V_I\leq 0$.

To accomplish controller $\tau_{r_{i}}$,we introduce the error variable

\begin{align} \label{E39} r_{e_{i}}=r_{i}-\bar r_i \end{align}

(39)

that should be driven to 0,and we re-write (27) as

\begin{align*} \label{E40} {{\dot V}_I}& = \sum\limits_{i = 1}^n {\tan \frac{{{\alpha _i}}}{2} \left( {{\Delta _{{r_i}}}-{\bar r}_i-r_{e_{i}}} \right)} + \notag\\ &\sum\limits_{i = 1}^n {\Delta _{{\beta _i}}}\Big( {\tau _{{\beta _i}}}- \frac{{{m_{{\upsilon _i}}}}}{{{m_{{u_i}}}}}({{\bar r}_i} +{r_{{e_i}}})+ \nonumber\\ & ({{\bar r}_i} + {r_{{e_i}}})\left( {\frac{{{m_{{\upsilon _i}}}}}{{{m_{{u_i}}}}}-\frac{{{m_{{u_i}}}}}{ {{m_{{\upsilon _i}}}}}} \right){\cos ^2}{\beta _i} + \left( {\frac{{{d_{{u_i}}}}}{{{m_{{u_i}}}}}- \frac{{{d_{{\upsilon _i}}}}}{{{m_{{\upsilon _i}}}}}} \right)\nonumber\times\\ & { \sin {\beta _i} \cos {\beta _i}} \Big) + \sum\limits_{m \in \mathcal L} \left( {{\eta _m}-{\eta ^*}} \right)\left( {\Delta _{{\tau _{tm}}}} + \frac{1}{{\eta _m^2}}\frac{{\partial {\xi _m}}}{{\partial {s_m}}}\left( {\tau _{{t_m}}} + \right.\right. \end{align*} \begin{align} &({{\bar r}_m} + {r_{{e_m}}})\left( {\frac{{{m_{{\upsilon _m}}}}}{{{m_{{u_m}}}}}-\frac{{{m_{{u_m}}}}}{{{m_{{\upsilon _m}}}}}} \right){\upsilon _{{t_m}}}\sin {\beta _m}\cos {\beta _m}-\nonumber\\ &\left( {\frac{{{d_{{u_m}}}}}{{{m_{{u_m}}}}}{{\cos }^2}{\beta _m}} {\left. {\left. { + \frac{{{d_{{\upsilon _m}}}}}{{{m_{{\upsilon _m}}}}}{{\sin }^2}{\beta _m}} \right){\upsilon _{{t_m}}}} \right)} \right) +\notag\\ & \sum\limits_{k \in \left\{ {\mathcal V-\mathcal L} \right\}} \left( {{\eta _k}-{{\hat \eta }_k}} \right)\nonumber\times\\ & \left( {{\Delta _{{\tau _{tk}}}} + } \right. \frac{1}{{\eta _k^2}}\frac{{\partial {\xi _k}}}{{\partial {s_k}}}\left( {{\tau _{{t_k}}} + ({{\bar r}_k} + {r_{{e_k}}})\left( {\frac{{{m_{{\upsilon _k}}}}}{{{m_{{u_k}}}}}-\frac{{{m_{{u_k}}}}}{{{m_{{\upsilon _k}}}}}} \right)} \right. {\upsilon _{{t_m}}}\times \nonumber\\ &\left. {\sin {\beta _k}\cos {\beta _k}-\left( {\frac{{{d_{{u_k}}}}}{{{m_{{u_k}}}}}{{\cos }^2}{\beta _k} + \frac{{{d_{{\upsilon _k}}}}}{{{m_{{\upsilon _k}}}}}{{\sin }^2}{\beta _k}} \right){\upsilon _{{t_k}}}} \right)\nonumber-\\ & \sum\limits_{k \in \left\{ {\mathcal V-\mathcal L} \right\}} {{\varphi _k}\left( {{{\dot {\hat \eta} }_k} + {k_0}\sum\limits_{j = 1}^n {{a_{kj}}\left( {{\xi _k}-{\xi _j}} \right)} } \right)}. \end{align}

(40)

Substituting (32) $\sim$ (35) and (38) into (40) results in \begin{align*} {{\dot V}_I}&=-k_1 \sum\limits_{i = 1}^n {\frac{{\sin ^2 \frac{{\alpha _i }}{2}}}{{\cos \frac{{\alpha _i }}{2}}}}-k_2 \sum\limits_{i = 1}^n \Delta _{\beta _i} ^2-k_3 \sum\limits_{m \in\mathcal {L}} {\left( {\eta _m-\eta ^* } \right)^2 }-\nonumber \\ & k_3 \sum\limits_{k \in \left\{ {\mathcal {V}-\mathcal {L}} \right\}}^n {\left( {\eta _k-\hat \eta _k } \right)^2 }-k_4 (\pmb{\eta} -\eta^*\pmb{1}_n)^{\rm T} L(\pmb{\eta}-{\eta}^*\pmb{1}_n)+ \nonumber\\ & \sum\limits_{m \in \mathcal {L}} {r_{e_m } \Delta _{r_{em} }}+\sum\limits_{k \in \left\{ {\mathcal {V}-\mathcal {L}} \right\}}{r_{e_k } \Delta _{r_{ek} }}, \end{align*} where

\begin{align} \label{E43} \Delta _{r_{em} } & = \left( {\eta _m-{\eta} ^{*} } \right)\frac{1}{{\eta _m^2 }}\frac{{\partial \xi _m }}{{\partial s_m }}\left( {\frac{{m_{\upsilon _m } }}{{m_{u_m } }}-\frac{{m_{u_m } }}{{m_{\upsilon _m } }}} \right)\upsilon _{t_m } \sin \beta _m \times \nonumber \\ & \cos \beta_m-\tan\frac{\alpha _m }{2}+\notag\\ &\Delta _{\beta _m}\left(-\frac{{m_{\upsilon _m } }}{{m_{u_m } }}+\left( {\frac{{m_{\upsilon _m } }}{{m_{u_m } }}-\frac{{m_{u_m } }}{{m_{\upsilon _m } }}} \right)\cos ^2 \beta _m\right), \end{align}

(41)

\begin{align} \label{E44} \Delta _{r_{ek} } & = \left( {\eta _k-\hat{\eta} _k } \right)\frac{1}{{\eta _k^2 }}\frac{{\partial \xi _k }}{{\partial s_k }}\left( {\frac{{m_{\upsilon _k } }}{{m_{u_k } }}-\frac{{m_{u_k } }}{{m_{\upsilon _k } }}} \right)\upsilon _{t_k } \sin \beta _k \cos \beta_k-\nonumber \\ & \tan\frac{\alpha _k }{2}+ \Delta _{\beta _k}\left( {-\frac{{m_{\upsilon _k } }}{{m_{u_k } }} + \left( {\frac{{m_{\upsilon _k } }}{{m_{u_k } }}-\frac{{m_{u_k } }}{{m_{\upsilon _k } }}} \right)\cos ^2 \beta _k } \right). \end{align}

(42)

Step 2. Backstepping for $r_{e_{i}}$. Consider a second control Lyapunov function given by

\begin{align} \label{E41} V_{II} = V_I + \frac{1}{2}\sum\limits_{i = 1}^n {r_{e_i }^2 }. \end{align}

(43)

Differentiating (41) along the solutions of (32) $\sim$ (35) and (38),we have

\begin{align} \label{E42} \dot{V}_{II}=&-k_1 \sum\limits_{i = 1}^n {\frac{{\sin ^2 \frac{{\alpha _i }}{2}}}{{\cos \frac{{\alpha _i }}{2}}}}-k_2 \sum\limits_{i = 1}^n \Delta _{\beta _i} ^2-k_3 \sum\limits_{m \in\mathcal {L}} {\left( {\eta _m-\eta ^* } \right)^2 } \nonumber-\\ & k_3 \sum\limits_{k \in \left\{ {\mathcal {V}-\mathcal {L}} \right\}}^n {\left( {\eta _k-\hat \eta _k } \right)^2 }-k_4 (\pmb{\eta}-\eta^*\pmb{1}_n)^{\rm T} L(\pmb{\eta}-{\eta}^*\pmb{1}_n) \nonumber+\\ &\sum\limits_{m \in \mathcal {L}} {r_{e_m }\left(\Delta _{r_{em} }+g_{r_{m}}+\frac{1}{m_{r_{m}}}\tau_{r_{m}}-\dot{\bar{r}}_{m}\right)}\nonumber +\\ &\sum\limits_{k \in \left\{ {\mathcal {V}-\mathcal {L}} \right\}} {r_{e_k }\left(\Delta _{r_{ek} }+g_{r_{k}}+\frac{1}{m_{r_{k}}}\tau_{r_{k}}-\dot{\bar{r}}_{k}\right)}. \end{align}

(44)

We set

\begin{align} \label{E45} \tau_{r_{i}}=-\frac{1}{m_{r_{i}}}\left(\Delta _{r_{ei} }+g_{r_{i}}-\dot{\bar{r}}_{i}+k_{5}r_{e_{i}}\right), \end{align}

(45)

where $k_{5}>0$. Then the time derivative of $V_{II}$ becomes

\begin{align} \label{E47} \dot{V}_{II}=&-k_1 \sum\limits_{i = 1}^n {\frac{{\sin ^2 \frac{{\alpha _i }}{2}}}{{\cos \frac{{\alpha _i }}{2}}}}-k_2 \sum\limits_{i = 1}^n \Delta _{\beta _i} ^2-k_3 \sum\limits_{m \in\mathcal {L}} {\left( {\eta _m-\eta ^* } \right)^2 } \nonumber-\\ & k_3 \sum\limits_{k \in \left\{ {\mathcal {V}-\mathcal {L}} \right\}}^n {\left( {\eta _k-\hat \eta _k } \right)^2 }-k_4 (\pmb{\eta}-\eta^*\pmb{1}_n)^{\rm T} L(\pmb{\eta}-{\eta}^*\pmb{1}_n)-\nonumber\\ & k_5 \sum\limits_{i = 1}^n {r_{e_i }^2}\leq 0. \end{align}

(46)

C. Stability Analysis

Under the coordinated controllers (33) $\sim$ (35),(38) and (45), the closed-loop equation of $f_{i}$ is denoted as

\begin{align} \label{E48a} \dot f_i = \left\| {\nabla f_i } \right\|\upsilon _{t_i} \sin \alpha _i. \end{align}

(47a)

The closed-loop equation of $\alpha_{i}$ is

\begin{align} \label{E48b} \dot \alpha _i = \upsilon _{t_i } \left( {k_{ai} \cos \alpha _i + k_{bi} \sin \alpha _i } \right) +k_2\Delta_{\beta_i}-r_i \end{align}

(47b)

with the dynamics of $r_i$ satisfying (32). The closed-loop equation of the relative generalized arc-length is

\begin{align} \label{E48c} &\dot { {\xi}} _i-\dot { {\xi}} _j = \eta _i +d_{\eta_i}-\eta _j -d_{\eta_j}. \end{align}

(47c)

The closed-loop equation of $\eta _m~(m\in\mathcal {L})$ satisfies

\begin{align}\label{E48d}\hskip-2mm\dot{\eta} _m =&-{\eta} _m^{2}\left[\left( {\cos \alpha _m \!+\! \frac{{\partial s_m }}{{\partial f_m }}\left\| {\nabla f_m } \right\|\sin \alpha _m } \right)\sum_{j = 1}^n a_{mj}\times \right.\nonumber\\ &\left. \left(\xi _m-\xi _j\right)+ k_2 \left( {\eta _m-\eta^* } \right) +k_3\sum_{j=1}^n a_{mj}(\eta _m-\eta _j) \right]. \end{align}

(47d)

The closed-loop equation of ${\eta} _k~(k\in\{\mathcal {V}-\mathcal {L}\})$ is

\begin{align} \label{E48e}\dot{\eta} _k =& {\eta} _k^{2}\left[\frac{\dot{\hat{\eta}}_k}{\eta_{k}\hat{\eta}_k}-\left( {\cos \alpha _k \!+\! \frac{{\partial s_k }}{{\partial f_k }}\left\| {\nabla f_k } \right\|\sin \alpha _k } \right)\sum_{j = 1}^n a_{kj}\times\right.\nonumber\\ & \left. \left( \xi _k-\xi _j \right)-k_2 \left( {\eta _k- \hat{ \eta}_k } \right)-k_3\sum_{j=1}^n a_{ij}(\eta _k-\eta _j) \right]. \end{align}

(47e)

And the closed-loop equation of the relative attitude is

\begin{align} \label{E48f} &\dot {\beta}_{i}^{\alpha}-\dot {\beta}_{j}^{\alpha} =-k_2 \left( {\sum\limits_{j = 1}^n {a_{ij} \left( {\beta _{i}^{\alpha}- \beta_{j}^{\alpha} } \right)-\tan \frac{\alpha _i }{2} } } \right)\nonumber+ \\ &~~~~~~~~ k_2\left( {\sum\limits_{i = 1}^n {a_{ji} \left( {\beta_{j}^{\alpha}-\bar \beta_{i}^{\alpha} } \right)-\tan \frac{\alpha _j }{2} } } \right). \end{align}

(47f)

Theorem 1. Consider a set of level curves of orbit function constructed from each given orbit through concentric compression design. Assume the generalized arc-lengths meet Assumption 1 and the reference state $\eta^{*}$ is a time-invariant signal that is greater than $0$. Suppose the initial conditions of fully actuated surface vessels make the initial value of $V_{II}$ given in (41) finite. Then the coordinated control problem along orbits is solved via the path-following control (45),the attitude synchronization control (33) and the formation control (34),(35) with the coordinated adaptation control (38),if the communication topology is connected and at least one vessel has access to $\eta^{*}$.

Proof. Set $\Phi = \{( f_{i},\alpha_{i},\xi_{i}-\xi_{j},\eta_{m}-\eta^*,\eta_{k}-\hat{\eta}_k, \beta_{i}^{\alpha}-\beta_{j}^{\alpha},\varphi_k,r_{e_{i} }) | V_{II} \le c \}$ for $c>0$ is closed by continuity. Since $\alpha _i$ is defined in $\left(-\pi,\pi\right]$,$\left| {f_i } \right| < \varepsilon_i$ due to the boundedness of $V_{II}$,$\left| {\xi _i-\xi _j } \right| \le \sqrt {4c/k_0 } $ , $\left|r_{e_{i}}\right|\le \sqrt {2c }$ ,$\left| {\beta_{i}^{\alpha}-\beta_{j}^{\alpha} } \right| \le \sqrt {4c }$ ,$\left|\varphi_k\right|\le \sqrt {2c }$ ,$\left| \eta _m \right| \le h_{\eta _m } ^{-1} (c )+|{\eta} ^*|$ where $m\in\mathcal {L}$,and $h_{\eta _m}={\ln\left(\eta_{m}/{\eta}^{*}\right)+{\eta}^{*}/\eta_{m}-1}$, $\left| \eta _k \right| \le h_{\eta _k } ^{-1} (c )+|\hat{\eta} _k|\le h_{\eta _k } ^{-1} (c )+\sqrt {2c }+|{\eta} ^*|$,where $k\in\{\mathcal {V}-\mathcal {L}\}$ and $h_{\eta _k }={\ln\left(\eta_{k}/\hat{\eta}_k\right)+\hat{\eta}_k/\eta_{k}-1}$, set $\Phi _I $ is compact. On the compact set $\Phi _I $,$|\partial s_i( {f_i ,\phi _i })/{\partial f_i }|$ and $|\partial ^2 s_i({f_i ,\phi _i})/{\partial f_i^2 }|$ are bounded because $\phi _i \in \left[{0,2\pi } \right)$. $\left\| {\nabla f_i } \right\|$ is bounded by continuity. Since ${\partial \xi _i}/{\partial s_i }$ is bounded and greater than $0$,$\upsilon _{t_i} = \left( {\frac{{\partial \xi _i }} {{\partial s_i }}} \right)^{-1} \eta _i $ is also bounded on $\Phi $. Thus the closed-loop system (47) is Lipschitz continuous on set $\Phi $, and a solution exists and is unique. Notice that the value of $V_{II}$ is time-independent and non-increasing,the entire solution stays in $\Phi $ when the initial value of $V_{II}$ is finite. Thus we conclude that (8) is tenable by Conditions 1 and 2,and $\upsilon _{t_i}$ is always nonzero due to that $\eta_i>0$ all the time,which implies that (5) is satisfied. Applying the invariance-like theorem,it follows that the trajectories of closed-loop system will converge to the set inside the region $E = \{ ( f_{i},\alpha_{i},\xi_{i}-\xi_{j},\eta_{m}-\eta^*,\eta_{k}-\hat{\eta}_k,\beta_{i}^{\alpha}-\beta_{j}^{\alpha},\varphi_k,r_{e_{i} })\left| {\dot V_{II} = 0} \right. \}$,that is,

\begin{align} \label{E49} \alpha _i = 0,{\beta}_i^{\alpha}-{\beta}_j^{\alpha}=0, \eta _m = \eta ^* ,\eta _k =\hat{\eta}_k ,\eta _i=\eta _j, r_{e_{i}}=0, \end{align}

(48)

as $t\rightarrow\infty$. From (48),it is obvious that $\hat{\eta}_k=\eta^*$,because $\eta _m = \eta ^* $,$\eta _k =\hat{\eta}_k$ and $\eta _i=\eta _j$. By noticing that $r_{i}\rightarrow \bar{r}_{i}$ as $r_{e_{i}}\rightarrow 0$,on set $E$,the closed-loop system becomes

\begin{align} \label{E50a} \dot f_i = 0, \end{align}

(49a)

\begin{align} \label{E50b} \dot \alpha _i =-2\nabla h_i \upsilon _{t_i } \left\| {\nabla f_i } \right\|-2k_0\eta ^* \frac{{\partial s_i }}{{\partial f_i }}\left\| {\nabla f_i } \right\|\sum\limits_{j = 1}^n {a_{ij} \left( {\xi _i-\xi _j } \right)}, \end{align}

(49b)

\begin{align} \label{E50c} \dot \xi _i-\dot \xi _j = \eta _i-\eta _j, \end{align}

(49c)

\begin{align} \label{E50d}\dot \eta _i =-(\eta ^*)^{2} k_0\sum_{j = 1}^n {a_{ij} \left( {\xi _i-\xi _j } \right)}, \end{align}

(49d)

\begin{align} \label{E50e}\dot{ \beta }_i^{\alpha}-\dot {\beta }_j^{\alpha} = 0. \end{align}

(49e)

Firstly,we will show that $\xi _i-\xi _j \to 0$ as $t\rightarrow\infty$. Since (49c) implies $\dot \xi _i-\dot \xi _j = \eta _i-\eta _j = 0$ on set $E$,$\xi _i-\xi _j $ is a constant. Then from (49d) $\dot \eta _i $ is uniformly continuous. By the extension of the Barbalat lemma^[24],$\dot \eta _i \rightarrow 0$ as $t\rightarrow\infty$,that is,$(\eta ^*)^{2}\sum_{j = 1}^n {a_{ij} \left( {\xi _i-\xi _j } \right)}=0$. Due to $\eta ^*\neq 0$,one has $L\xi=0$. If the communication graph is connected,we have $\xi _i-\xi _j \to 0$ as $t\rightarrow\infty$.

Next,we will prove $f_i \to 0$ as $t\rightarrow\infty$. Since $\xi _i-\xi _j = 0$ on set $E$,from (49b) one has

\begin{align} \label{E51} \dot \alpha _i =-2\nabla h_i \upsilon _{t_i } \left\| {\nabla f_i } \right\|. \end{align}

(50)

It is easy to check that $\lim_{t\rightarrow\infty}\upsilon_{t_i}=(\partial \xi/\partial s_i)\eta^*> 0$ is uniformly continuous and bounded from Assumption 1. From (49a),$f_i$ tends to be a constant and thus $\nabla h_i $ tends to be a constant. Therefore,$-2\nabla h_i \upsilon _{t_i} \left\| {\nabla f_i } \right\|$ is uniformly continuous. According to (50),we have $\dot{\alpha_{i}} \to 0$ as $t\rightarrow\infty$ based on the extension of the Barbalat lemma^[24]. Thanks to $ {\lim }_{t \to \infty } \upsilon _{t_{i}} \left\| {\nabla f_i } \right\| \ne 0$,$\nabla h_i \to 0$ as $t\rightarrow\infty$. By Condition 3,$f_i$ tends to be $0$.

Ⅳ. SIMULATION RESULTS

In this section,we apply the proposed control law to coordinating four fully actuated surface vessels moving along a set of given orbits with a desired formation and attitude pattern. The communication topology is shown in Fig. 5 and the first vessel has access to the reference state $\eta^*=0.5$.

The given orbits for vessels are concentric ellipses (11) where $a=3$,$b=2$,$R_i= 1 + 0.5\left( {i-1} \right)~(i=1,2,3,4)$. We demand the family of vessels to form a trapezia formation pattern and achieve attitude synchronization. From the desired pattern,we select the generalized arc-lengths as $\xi _i = s_i/R_i +\Delta_{s_i}$,where $\Delta_{s_1}=\Delta_{s_4}=0$, $\Delta_{s_2}=\pi/6$,$\Delta_{s_3}=\pi/12$,and the starting point is the intersection of the orbit with the positive semi-major axis. We choose the desired attitude scalars as $\beta_{i}^{*}=0$. The reference orbital velocity is $\eta^{*}=0.5$. The mode and control parameters are selected as $m_{u_{i}}=24,~m_{\upsilon_{i}}=34,~m_{r_{i}}=3,~m_{u\upsilon_{i}}=1, ~d_{u_{i}}=2,~d_{\upsilon_{i}}=7,~d_{r_{i}}=0.5$, $k_{j}=10~(j=0,\cdots ,5)$.

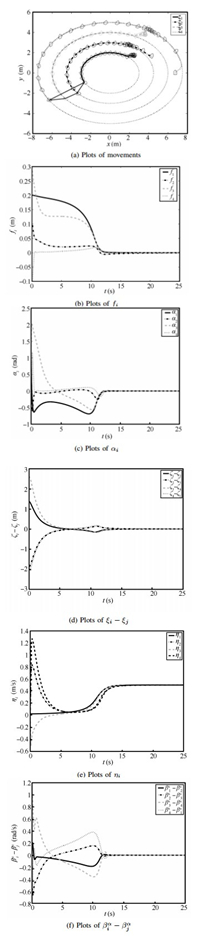
The movement of vessels is shown in Fig. 6 (a). From this figure,we can see that four vessels finally move along the set of given loops drawn by the real lines,form the desired formation denoted by the dashed lines and achieve attitude synchronization when the system reaches the steady state. The path-following errors $f_{i}$ and $\alpha_{i}$ tend to be 0 as plotted in Figs. 6 (b) and 6 (c),respectively. Fig. 6 (d) demonstrates that $\xi_{i}$ reaches consensus,and Fig. 6 (e) shows $\eta_{i}$ converges to the reference value. The relative attitudes ${\beta}_{i}^{\alpha}-{\beta}_{j}^{\alpha}$ converge to 0 as shown in Fig. 6 (f). According to these figures,we can conclude that the coordinated control problem along orbits can be solved via our proposed controller.

Ⅴ. CONCLUSION

In this paper,we develop our previous concentric-compression-based design^[18] to deal with coordinated path-following and attitude synchronization control of multiple fully actuated surface vessels. By using the potential function,we remove the assumption of nonzero total line velocity of each vessel. A coordinated adaptive scheme is given to solve the problem that only a portion of vessels in the team have access to the reference time-invariant orbital velocity,which makes our proposed control more scalable and distributed. In our ongoing work,we seek to improve our method in order to deal with the reference time-variant orbital velocity.