2. Duke University, Durham, USA;
3. Massachusetts Institute of Technology, Cambridge, USA;
Reinforcement learning (RL)[1] in continuous or large state spaces often relies on function approximation to maintain a compact model of the value ($Q$) function[2, 3, 4]. The performance of approximate RL algorithms employing fixed feature function approximators,such as radial bases function networks with a priori distributed centers,often depends on the choice of those features,which can be difficult to allocate. Gaussian processes (GPs)[5] are Bayesian nonparametric (BNP) models that are capable of automatically adjusting features based on the observed data. GPs have been successfully employed in high-dimensional approximate RL domains,such as a simulated octopus arm[6],but several aspects of their use,particularly convergence guarantees and off-policy learning have not been fully addressed.
More specifically,unlike RL algorithms employing a tabular representation,and even some function approximation techniques[3, 7],no convergence results for RL algorithms with GPs exist. Also,existing RL methods with GPs have either required burdensome computation in the form of a planner[8, 9, 10] or require that the policy being learned is the same as the one being executed (on-policy learning)[6]. The latter approach is less general than off-policy RL,which enables learning the optimal value function using samples collected with a safe or exploratory policy.
In this paper,we present a method for approximate RL using GPs that has provable convergence guarantees in the off-policy setting. More specifically,a model-free off-policy approximate reinforcement learning technique,termed as GPQ,that uses a GP model to approximate the value function is presented. GPQ does not require a planner,and because it is off-policy,it can be used in both online or batch settings even when the data is obtained using a safe or exploratory policy. In addition,we present an extension of GPQ that uses a heuristic exploration strategy based on the GP's inherent measures on predictive confidence. In addition to presenting the GPQ framework,sufficient conditions for convergence of GPQ to the best achievable optimal Q-function given the data ($Q^*$) are presented in the batch and online setting,and it is shown that these properties hold even if new features are added or less-important features removed to maintain computational feasibility. Our work also contributes to off-policy approximate RL in general,because unlike other recent papers on off-policy RL with fixed-parameter linear function approximation[4, 11, 12, 13],our approach allows the basis functions to be automatically identified from data. Furthermore,our condition for convergence reveals why in the batch case GPQ or kernel base fitted Q-Iteration[3] could lead to divergence in the worst case,and how the divergence can be prevented by tuning a regularization-like parameter of the GP. A practical online implementation of this framework that makes use of a recent budgeted online sparse GP inference algorithm[14] is empirically demonstrated,and it is theoretically shown how the sparsification affects GPQ's performance in the batch case. Our theoretical and empirical results show off-policy RL using a GP provides provable convergence guarantees and competitive learning speeds.
II. BACKGROUNDThe problem of sequential decision making under uncertainty can be formulated as a Markov decision process (MDP)[1]: $\mathcal{M} = \left\langle {\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma } \right\rangle $,with state space $\mathcal{S}$,action set $\mathcal{A}$,transition function $\mathcal{P} = p(s_{t+1}|s_t,a_t)$,reward function $\mathcal{R}(s,a) \mapsto {\bf R}$,and discount factor $\gamma \in [0,1)$. A deterministic policy $\pi :\mathcal{S} \to Pr[\mathcal{A}]$ maps states to actions. Together with the initial state $s_0$,a policy forms a trajectory $\zeta = \{[s_0,a_0,r_0],[s_1,a_1,r_1],\cdots\}$ where $a_t = \pi(s_t)$,and both $r_t$ and $s_t$ are sampled from the reward and transition functions.
The state-action value function or Q-function of each state-action pair under policy $\pi$ is defined as ${\rm Q}^\pi(s,a) = {\rm E}_\pi \left[\sum_{t = 0}^\infty {\gamma^t r_{t+1}(s_{t+1},a_{t+1})}|s_0=s,a_0=a\right]$ which is the expected sum of discounted rewards obtained starting from state $s$,taking action $a$ and following $\pi$ thereafter. The optimal Q-function $Q^*$ satisfies $Q^*=\max_\pi Q^\pi(s,a)$ and is captured by the Bellman equation: ${Q^*}\left( {s_t,a_t} \right) = {\rm E}_{s_{t+1}} \left[{r(s_t,a_t) + \max_{a'} \gamma Q^*\left( {s_{t+1},a'} \right)} \right]$.
Throughout this paper,bounds are derived on $||\hat{Q}-Q^*||$ where $\hat{Q}$ is an approximation of $Q^*$. Deriving such bounds provides a bound on the value of the optimal policy derived from $\hat{Q}$ when it is executed in the real world,specifically an error factor of $\frac{2\gamma||\hat{Q}-Q^*||}{1-\gamma}$ is introduced[15].
A. Reinforcement LearningReinforcement learning is concerned with finding the optimal policy $\pi^*(s) = \arg\,\max_a Q^{*}(s,a)$ when $\mathcal{P}$ and $\mathcal{R}$ are unknown. In {online} RL,an agent chooses actions to sample trajectories from the environment. In batch RL,a collection of trajectories is provided to the learning agent. In either case,model-free value-based reinforcement learning methods update an estimate of $Q(s,a)$ directly based on the samples. When an RL method learns the value function of the same policy with which samples were collected,it is classified as on-policy; when the policy employed to obtain samples is different,it is termed off-policy. For instance,the Q-learning algorithm[16] performs an off-policy update of the form $Q_{t+1}(s_t,a_t)=Q_t(s_t,a_t)+\alpha_t\Delta_t$,{with a time dependent learning rate $\alpha_t$} and temporal difference (TD) error $\Delta_t = r(s_t,a_t)+\gamma\max_{a'}\big(Q_t(s_{t+1},a')\big)-Q_t(s_t,a_t)$,{where $a'$ is the action that maximizes $\big(Q_t(s_{t+1},a')\big)$.} The on-policy counterpart to Q-learning is SARSA[1],which uses a different TD error based on the current policy: $\Delta_t = r(s_t,a_t)+\gamma\big(Q_t(s_{t+1},a_{t+1})\big)-Q_t(s_t,a_t)$. Off-policy algorithms can be used in situations where batch data or "safe" exploration policies are used.
For continuous RL domains,linear value function approximation is often used to model the Q-function as a weighted combination of fixed bases $\phi(s,a)$,that is $Q(s_t,a_t)=\phi^{\rm T}(s_t,a_t)\theta$. Then,the off-policy gradient descent operation from Q-learning can be used to update $\theta$ using the following TD error with $\phi_t = \phi(s_t,a_t)$: $\Delta_t=( r_t+\gamma\max_{a'}\phi^{\rm T}_{{t+1}_{\max\theta_t}}\theta_t)-\phi^{\rm T}_t\theta_t$. However,function approximation can cause divergence for off-policy RL methods,including Q-learning and linear-least squares approaches[17, 18]. It is possible to guarantee convergence of some off-policy algorithms under certain constraints. For instance,Melo et al.[7] provide sufficient conditions for approximate Q-learning's convergence: ${\rm E}_\pi\left[\phi_t\phi^{\rm T}_t\right]\geq\gamma^2{\rm E}\left[\phi_{t_{\max\theta_t}}\phi^{\rm T}_{t_{\max\theta_t}}\right]$. This generally requires the initial policy to be very close to $\pi^*$ and is heavily tied to the choice of bases. The potential for divergence in off-policy settings can limit the applicability of RL algorithms to safety critical domains.
B. Related WorkA series of papers[2, 6] showed GPs could be used to capture the value function using on-policy updates,specifically SARSA and approximate policy iteration,which may not be able to learn the value of a new policy from batch data. Others have used GPs in model-based RL to learn the MDP parameters ($\mathcal{P}$ and $\mathcal{R}$)[8, 10],including a variant of the $R_{\max}$ algorithm that explored through an "optimism in the face of uncertainty" heuristic[9]. However,model-based approaches require a planner to determine the best action to take after each update,which could be computationally costly.
Several recent approaches ensure convergence in the online case by adding some form of regularization to TD algorithms for policy evaluation,as done in TDC[13]; GQ[4],LARS-TD[11],and RO-TD[12]. These algorithms use different versions of the SARSA-style TD error,but the regularization ensures their convergence even when the samples are obtained off-policy. In contrast to these algorithms,the GPQ algorithm presented here is an off-policy learning algorithm that attempts to directly minimize the Q-learning TD error. This TD error,which is directly derived from the Bellman optimality equations,is better suited for off-policy learning because it is the best approximation to the optimal Q-function given the samples that have been seen. Furthermore,many existing approaches rely on a fixed set of bases stipulated at initialization. In particular,[4] assumed the existence of a fixed set of features and Liu et al.[12] assume a fixed set of features from which features of less value are removed. In contrast,GPQ leverages a BNP approach to automatically choose features based on the data. Other algorithms,such as Bellman error basis functions[19] dynamically construct features for linear function approximators,but these methods are primarily used in on-policy evaluation and,depending on their potential space of features,may not have the representational power of GPs. In the batch case,several algorithms belonging to the fitted Q-iteration (FQI) family of algorithms[3] can guarantee off-policy convergence with specific function approximators,including averagers[20] and certain forms of regularized least squares[21]. In contrast,our approach leverages GPs,which are powerful BNP function approximators. We show that Gaussian processes can,with a prescribed setting of one regularization parameter,guarantee convergence in the batch case (which can be related to an FQI-like algorithm) and then describe how to extend this batch algorithm to the online case. In the online case,Geist et al.[22] use a measurement model similar to GPQ and FQI,and handle the nonlinearity of that equation by using extended/unscented Kalman filter like approaches,which can potentially diverge.
In Section IV-B,we introduce an exploration method based on "optimism in the face of uncertainty" using GP confidence intervals. Others have used confidence intervals on the MDP parameters themselves in a similar way in the discrete-state case[23]. Previous work has done similar exploration using GPs in supervised learning[24] and the bandit setting with continuous actions[25],but the latter is only for single-state RL whereas we explore in a full MDP. Other RL exploration heuristics that utilize GP variance include a strategy based on information theory[26],which more explicitly targets uncertain areas,but was designed for on-policy RL and requires a model to calculate long-term information gains.
Although rooted in the Bayesian framework,GPs have a deep connection with reproducing kernel Hilbert space techniques[5],therefore,this work also augments the growing body of literature in Kernel based approximate MDPs and RL[27, 28, 29, 30].
C. Gaussian ProcessesGaussian processes (GPs)[5] are BNP function approximation models: they do not specify a model structure a priori and explicitly model noise and uncertainty. A GP is defined as a collection of random variables,any finite subset of which has a joint Gaussian distribution with mean (prediction) function $m(z)$ and covariance kernel,such as a radial basis function (RBF),$k(z',z)$,for input points $z$ and $z'$. In the case of modeling the Q-function,the input domain is the space of all state action pairs and the model captures a distribution over possible Q-functions.
Let $Z=[z_1,\cdots,z_\tau]$ be a set of state action pairs observed at discrete sample times,where each state action pair is concatenated as $z$ for ease of exposition. In our analysis,we assume a finite set of actions,but all analysis extends to the continuous action space as well. Let $\vec {\pmb y} = [y_1,\cdots ,y_\tau]^{\rm T}$ denote the vector of observation values at the respective state action pairs. Given some set of data points $\vec {\pmb y}$ at corresponding locations in the input domain $Z$,we would like to predict the expected value of the Q-function $y_{\tau+1}$ at some possibly new location $z_{\tau+1}$. Define $K(Z,Z)$ as the kernel matrix with entries $K_{l,m}=k(z_l,z_m)$. ${\pmb k}(Z,z_{\tau+1})\in{\bf R}^{\tau}$ denotes the kernel vector corresponding to the ${\tau+1}$-{th} measurement,and $\omega_n^2$ represents the variance of the uncertainty in our measurement. Using Bayes law and properties of Gaussian distributions,the conditional probability can be calculated as a normal variable[5] with mean $m(z_{\tau+1})=\alpha^{\rm T} {\pmb k}(Z,z_{\tau+1})$,where $\alpha=[K(Z,Z)+\omega_n^2 I]^{-1}\vec {\pmb y}$ are the kernel weights,and covariance
| \begin{align}\label{eq:gp_cov} & \Sigma(z_{\tau+1})={\pmb k}(z_{\tau+1},z_{\tau+1})+\notag\\ &\quad \omega_n^2-{\pmb k}^{\rm T}(Z,z_{\tau+1})[K(Z,Z)+\omega_n^2 I]^{-1} {\pmb k}(Z,z_{\tau+1}). \end{align} | (1) |
Performing batch prediction using GPs requires an expensive inversion of a matrix that scales as ${\rm O}(\tau^3)$ with the size of the data. Many sparsification schemes have been proposed to reduce this computational complexity to ${\rm O}(\tau m^2)$[31, 32],where $m$ is a number of reduced parameters. In this paper,we use the sparsification method of [14],which allows for sequential updates. This sparsification algorithm works by building a dictionary of basis vector points that adequately describe the input domain without including a basis point at the location of every observed data point. A full description of this algorithm is available in Appendix A. In order to determine when a new point should be added to the dictionary,a linear independence test is performed
| \begin{align}\label{eq:linearsol} &\beta_{\tau+1} = {\pmb k}(z_{\tau+1},z_{\tau+1})-\notag\\ &\quad {\pmb k}(Z_d,z_{\tau+1})^{\rm T} K(Z_d,Z_d)^{-1} {\pmb k}(Z_d,z_{\tau+1}),\end{align} | (2) |
when $\beta_{\tau+1}$ is larger than a specified threshold $\beta_{tol}$,then a new data point is added to the dictionary. Otherwise,the weights $\alpha_\tau$ are updated,but the dimensionality of $\alpha_\tau$ remains the same.
III. BATCH OFF-POLICY RL WITH A GPAs a slight abuse of notation,we let $Q^*$ represent the best possible representation of the true Q-function given the data available. In GPQ,we model $Q^*$ as a GP with mean function $m^*(s,a)$ and positive semi-definite covariance kernel $k([s,a],[s',a'])$. To do so,we place a zero mean Gaussian prior on $Q$,so $Q(s,a)\sim {\rm N}\big(0,k(\cdot,\cdot)\big)$. Our goal is to perform posterior inference using available information so that the current estimate of the mean $\hat{m}$ approaches the mean of $Q^*$. Let the current estimate of the mean of the Q-function be $\hat Q(s,a)=\hat{m}(s,a)$. Since samples of $Q^*$ are not available,posterior inference needs to be performed using the best estimate of $Q^*$ at the current time as
| \begin{equation}\label{eq:Qhat} \hat Q(s_t,a_t)=r(s_t,a_t)+\gamma\max_{a'}(\hat Q(s_{t+1},a')). \end{equation} | (3) |
Everytime we update the model of $\hat Q(s_t,a_t)$ with a new observation,the accuracy of the observation is dependent on the accuracy of the current model. Typically,the parameter $\omega_n^2$ is viewed as a uncorrelated,Gaussian measurement noise in GP literature. Here,we offer an alternative interpretation of $\omega_n^2$ as a regularization term which accounts for the fact that current measurements are not necessarily drawn from the true model and therefore prevents our model from converging too quickly to an incorrect estimate of $Q^*$. As we will show later,$\omega_n^2$ plays a pivotal role in preventing divergence.
We now consider using the update rule in (3) with a GP model in the batch setting.
Using GPs and the update rule in (3) in the batch setting gives us Algorithm 1,which we call GP-FQI because it is a member of the fitted Q-Iteration family of algorithms. At each iteration,the values of the stored points are updated based on the stored rewards and transitions as well as the previous iteration's approximation of the Q-values,which is the form of fitted Q-iteration.
Algorithm 1. Batch GPQ (GP-FQI)
1) Input: Experience tuples $\langle s,a,r,s' \rangle_{1,\cdots,N}$
2) Output: A GP representing $\hat{Q}^*$
3) $\hat{Q} \leftarrow $ Initialized GP
4) repeat
5) $\hat{Q}' \leftarrow $ Initialized GP
6) for each experience tuple $\langle s,a,r,s' \rangle_i$ do
7) $y_i = r_i + \gamma \max_b \hat{Q}(s',b)$
8) Train $\hat{Q}$ on all $(\langle s_i,a_i\rangle,y\rangle_i$
9) $\hat{Q} = \hat{Q}'$
10) until the convergence condition is satisfied
Algorithm 2. Online GPQ
1) for each time step $\tau$ do
2) Choose $a_{\tau}$ from $s_{\tau}$,using $\epsilon$-greedy exploration
3) Take action $a_{\tau}$,observe $r_{\tau}$,$s_{\tau+1}$
4) Let $z_{\tau} = \langle s,a\rangle$ and $y_{\tau} = r + \gamma \max_b \hat{Q}(s',b)$
5) if $\beta_{\tau+1} > \beta_{tol}$ then}
6) Add $z_{\tau}$ to the $\mathcal{BV}$ set
7) Compute $k_{z_{\tau+1}}$ and $\alpha_{\tau+1}$ according to [14]
8) if $|\mathcal{BV}|$ > Budget then
9) Delete $z_i \in \mathcal{BV}$ with lowest score according to [14]
10) Update $\hat Q(z_{\tau+1})=\sum_{i=1}^{\infty}\alpha_i k(z_i,\cdot)$
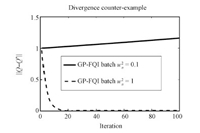
While convergence guarantees exist for some function approximators used in FQI,such as regression trees,others,such as neural nets,are known to be potentially divergent. Below,we prove that GP-FQI can diverge if the regularization parameter is not properly set. However,we also prove that for any set of hyperparameters and desired density of data,a proper regularization constant can be determined to ensure convergence. We begin with a counter-example showing divergence in the batch setting if $\omega_n^2$ is insufficient,but show convergence when $\omega_n^2$ is large enough.
Consider a system with three nodes located along the real line at locations $-1,0$,and $1$. At each time step,the agent can move deterministically to any node or remain at its current node. The reward associated with all actions is zero. All algorithms are initialized with $\hat Q(z) = 1,\forall z$,$\gamma = 0.9999$,and we use a RBF kernel with bandwidth $\sigma = 1$ in all cases. We consider two settings of the regularization parameter,$\omega_n^2 = 0.1$ and $\omega_n^2 = 1$. Fig. 1 shows that when $\omega_n^2$ is set too low,the Bellman operation can produce divergence in the batch setting. If the regularization is set to the higher value,GP-FQI converges. In the following sections,we show that determining the sufficient regularization parameter $\omega_n^2$ depends only on the density of the data and the hyperparameters,not the initialization value of $\hat Q$ or $\gamma$.
|
Download:
|
| Fig. 1. The maximum error $\|\hat Q - Q^*\|$ is plotted for GP-FQI with insufficient regularization $\omega_n^2 = 0.1$ and sufficient regularization $\omega_n^2 = 1$. | |
Let $T$ denote the approximate Bellman operator that updates the mean of the current estimate of the Q-function using the measurement model of (3),that is $\hat m_{k+1}=T\hat m_{k}$,we argue that $T$ is a contraction,so a fixed point exists. For a GP model,we define the approximate Bellman operator in the batch case as training a new GP with the observations $y_i = r(s_i,a_i) + \gamma \max_b \hat Q(s'_i,b)$ at the input locations $z_i = (s_i,a_i)$.
In the following theorem,we show that in the case of finite data,a finite regularization term always exists which guarantees convergence. In the next theorem,we show that a finite regularization tern exists for a sparse GP that only adds kernels when the tolerance threshold Ptol is excedded . In Theorem 3,we show that a finite bound exists,but do not compute the bound exactly as this depends on the topology of the space and kernel function.
Theorem 1. Given a GP with data $Z$ of finite size $N$,and Mercer kernel that is bounded above by $k_{\max}$,there exists a finite regularization parameter $\omega_n^2$ such that $T$ is a contraction in the batch setting. In particular,$\omega_n^2 = 2(\|K(Z,Z)\|_\infty-k_{\max}) \leq 2N$.
Proof. Let $\|(\cdot)\|$ denote the infinity norm. Consider the approximate Bellman operator $T$
| \begin{align} & \|TQ(Z)-TP(Z)\|=\|K(Z,Z)(K(Z,Z) + \notag\\ &\quad\omega_n^2I)^{-1}(\gamma Q(Z')-\gamma P(Z'))\|\leq\notag\\ &\quad\gamma \|K(Z,Z)\| \| (K(Z,Z) + \notag\\ &\quad\omega_n^2I)^{-1}\| \|(Q(Z)-P(Z))\|,\end{align} | (4) |
If $\|K(Z,Z)\| \| (K(Z,Z) + \omega_n^2I)^{-1}\| \leq 1$,then $T$ is a contraction. By the structure of the kernel,we know $\|K(Z,Z)\| = \max_j \sum_i k(z_j,z_i)$ for finite data,the sum is a finite sum of finite numbers,so $\|K(Z,Z)\|$ is finite. For the second term,we assume that $\omega_n^2$ is large and use [33] to bound the infinity norm of an inverse matrix that is strictly diagonally dominant. In order to be considered strictly diagonally dominant,a matrix $A$ must have the property $a_{ii} > \sum_{j\neq i} a_{ij}$,$\forall i$. In this case,
| \begin{align} & \| (K(Z,Z) + \omega_n^2I)^{-1}\| \leq\notag\\ &\quad \frac{1}{k_{\max}+ \omega_n^2-(\|K(Z,Z)\|-k_{\max})}. \end{align} | (5) |
Therefore,setting $\omega_n > 2\|K(Z,Z)\|-2k_{\max}$,we have
| \begin{align} \|TQ(Z)-TP(Z)\|\leq\gamma \| Q(Z)-P(Z)\|. \end{align} | (6) |
Theorem 2. Given a GP with infinite data generated using a sparse approximation with acceptance tolerance $\beta_{tol}$,and given a Mercer kernel function that decays exponentially,there exists a finite regularization parameter $\omega_n^2$ such that $T$ is a contraction in the batch setting.
Proof. To prove a contraction,we prove that $\|K(Z,Z)\|$ is finite,so by Theorem 1 there exists a finite $\omega_n^2$ such that (4) is a contraction. The norm of $\|K(Z,Z)\|$ is given by $\|K(Z,Z)\| = \max_j \sum_i k(z_j,z_i)$. We argue that the sum is convergent for an infinite number of data points selected using the linear independence test in (12). As the volume of the input domain increases to infinity,the number of data points added by a sparse selection increases polynomially,due to Ehrhart's theorem,while the value they add to the sum decays exponentially fast. This means that the sum is convergent as the number of BV goes to infinity. The result follows from Theorem 1. For details,the reader is referred to Appendix B.1.
Theorem 2 provides a powerful insight into the convergence properties of GPs. As the density of basis vectors increases or as the bandwidth of the kernel function grows,corresponding to decreasing $\beta_{tol}$,the basis vector weights $\alpha_i$ becomes increasingly correlated. As the weights become correlated,changing the weight at one basis vector also changes the weights of nearby basis vectors. It is this sharing of weights that can result in divergence,as seen in [17] . Theorem 2 shows that for a given $\beta_{tol}$ and kernel function,there exists a finite regularization parameter $\omega_n^2$ that will prevent divergence,however. This regularization technique can also be applied to provide convergence guarantees for FQI using a linear function approximator. In related work,[34] provides convergence guarantees for linear FQI using a similar regularization technique solved using an optimization-based framework. In practice,$\omega_n^2$ does not have to be set very large to prevent divergence. Both Theorem 2 and [34] consider worst case analysis,which generally is not encountered in practice. For most applications,reasonable values of $\omega_n^2 \in [0.01,1]$ will prevent divergence. In the next theorem,we bound the approximation error from using a sparse representation of a GP versus a full GP.
Theorem 3.If the sparse GP algorithm is used,the error $\|{\rm E} [\hat Q-Q^*]\|$ is uniformly,ultimately bounded for the approximate Bellman operator.
Proof. Let $\hat Q(s_t,a_t)=\hat Q_t$ for notational convenience. ${\rm E}[Q^*] = m^*(z)=\sum_{i\in \mathcal{BV}}{\pmb k}^{\rm T}(Z,z_i)\alpha^*_i+\sum_{i\not \in \mathcal{BV}}{\pmb k}^{\rm T}(Z,z_i)\alpha^*_i$. Let $V(Q_t)=\|{\rm E}[\hat Q_t-Q_{\mathcal{BV}}^*]\|_{\infty}$ be a positive definite Lyapunov candidate. Let $T$ denote the approximate Bellman operator applied to a sparse GP.
| \begin{align} &\|TE[\hat Q_t]-TE[Q^*]\| \leq\notag\\ &\quad \|T\|\|\gamma\max_{a'}\sum_{i\in \mathcal{BV}}{\pmb k}(Z,z)^{\rm T} (\alpha^t_i-\alpha^*_i)\|+\notag\\ &\quad\|\sum_{i\not \in \mathcal{BV}}{\pmb k}(Z,z_i)\alpha^*_i\|\leq\notag\\ &\quad \gamma\|T\|\|{\rm E}[\hat Q_t-Q^*_t]\|+|q_t|_\infty \beta_{tol},\end{align} | (7) |
where $q_t = (m(z_t)-\hat m(z_t))/(\Sigma(z_t))$ is the approximation error given in [7] . Let $c_1=\gamma\|T\|$ noting that $c_1 < 1$. Let $c_2=|q_t|\beta_{tol}$,which is finite. Hence $V(Q_{t+1})-V(Q_t)\leq (c_1-1)V(Q_t)+c_2$,indicating that whenever $\|{\rm E}[\hat Q_t-Q^*_{BV}]\| \geq \frac{c_2}{1-c_1}$,$V(Q_{t+1})-V(Q_t)\leq 0$. Therefore,the set $\left\{\hat Q_t: \|{\rm E}[\hat Q_t-Q^*_{BV}]\|\geq \frac{c_2}{1-c_1}\right\}$ is positively invariant,indicating that $Q_t$ approaches and stays bounded within a compact neighborhood of $Q^*$. Furthermore,as $\beta_{tol}\to 0$,$Q_t\to Q^*$ uniformly.
In the proof of Theorem 3,it should be noted that $q_{t_{\infty}}$ is always upper bounded. In particular,[35] shows that the upper bound on $q_{t_{\infty}}$ depends on the sparsification tolerance $\epsilon_{tol}$ in the online GP algorithm in [14] .
IV. ONLINE LEARNING WITH GPQIn the online case,an agent must collect data on its own,and the set of samples will increase in size. First consider a naive implementation of GP-FQI in the online setting in which at every step,we run the GP-FQI algorithm to convergence. This leads to the following changes to GP-FQI:
1) At each timestep $t$,the greedy action $a^* = \arg~\max_a \hat{Q}(s_t,a)$ is selected with probability $1-\epsilon$,and with probability $\epsilon$ a random action is chosen.
2) After each $\langle s,a,r,s' \rangle$ experience,$GP_a$ is updated by adding the point $s,a,r + \gamma \max_b \hat{Q}(s',b)$. Determine $\omega_n^2$ using Theorem 1 and perform GP-FQI as in Algorithm 1.
In the batch sequential version of GP-FQI,$\omega_n^2$ can be determined at each step by directly computing $\|K(Z,Z)\|$. Alternatively,one can use the linear independence test and only accept data points with $\beta_{\tau+1} \geq \beta_{tol}$. Given this knowledge,$\|K(Z,Z)\|$ can be computed a priori.
Corollary 1. If Theorem 1 and Theorem 2 hold,then GP-FQI converges in the batch sequential algorithm provided the data points are sufficiently dense in the domain: $\forall z \in S\times A: \exists c \in Z \text{ s.t. } k(z,z)-k(z,c)^2/k(c,c) \leq \beta_{tol}$.
At every iteration,GP-FQI will converge to a fixed estimate of $Q^*$ at the current data locations. Provided that the policy used for obtaining samples ensures ergodicity of the induced Markov chain,the algorithm will converge to an estimate of $Q^*$ everywhere. If we use a non-sparse GP with infinite data,we add the condition that there is zero probability of sampling a finite set of data points infinitely often in order to prevent $\|K(Z,Z)\|$ from growing to infinity. Additionally,if a sparse GP is used,then we know from Theorem 3 that our error is ultimately bounded.
A. Online GPQIn theory,GP-FQI provides a method with provable convergence,however the computational requirements can be intense. In our empirical results,we employ several approximations to GP-FQI to reduce the computational burden. We call this modified algorithm online GPQ and display it in Algorithm 2. At each step of online GPQ,we take an action according to some policy $\pi$ that ensures ergodicity of the induced Markov chain,and observe the value $y_{\tau} = r + \gamma \max_b \hat{Q}_\tau(s',b)$ at location $z_{\tau}$. The sparse online GP algorithm of [14] is used to determine whether or not to add a new basis vector to the active bases set $\mathcal{BV}$ and then update the kernel weights. We provide a set of sufficient conditions for convergence in the online case.
Theorem 4. For an ergodic sample obtaining policy $\pi$,and for each active basis set,a sufficient condition for convergence of $\hat m(z_t)\to m^*(z_t)$ as $t \to \infty$ online GPQ is ${\rm E}_\pi\left[C_tk_tk^{\rm T}_t+K_t^{-1}k_tk^{\rm T}_t\right]\geq\gamma {\rm E}_\pi\left[C_tk_tk^\alpha_t+K_t^{-1}k_tk^\alpha_t\right]$,where $k^\alpha_{t}\alpha_t=\max_{a'}(k^{\rm T}(x_{t+1},a'))\alpha_t$.
Here,$C_t$ is a negative definite and $K_t^{-1}$ is a positive definite matrix related to the posterior and the prior covariance explained in [14]. These sufficient conditions for convergence are less restrictive than [7] for Q-learning. The proof style follows closely to that of [7]. For details,the reader is referred to Appendix B.2.
It should be noted that while the convergence results presented here are significant because no such results have been available before,these results only guarantee the asymptotic convergence of the Q-function to the approximate Bellman operator's fixed point,within the projection of the selected bases. Which means the algorithm will eventually converge,yet no guarantees on the rate of convergence are provided here. Such guarantees are expected to depend on the choice of the exploration scheme,the algorithm's eventual selection of bases,and the rate at which the predictive variance decreases.
B. Optimistic Exploration for GPQThe online GPQ algorithm above used an $\epsilon$-greedy exploration strategy,which may not collect samples in an efficient manner. We now consider a more targeted exploration heuristic facilitated by the GP representation. Others have considered similar heuristics based on information theory 6. Here we use a simpler strategy based on the "optimism in the face of uncertainty" principle,which has been a cornerstone of efficient exploration algorithms (e.g.,[23]).
In the discrete-state case,optimistic value functions can be maintained by initializing Q-values to $R_{\max}/(1-\gamma)$ and performing updates that maintain optimism until the values are nearly accurate. Pairing this over-estimate with greedy action selection causes the agent to explore areas of the state space that may yield higher long-term values,but not at the expense of "known" areas which have higher values grounded in real data. We propose using the upper confidence tails from the GP as an optimistic value function. Specifically,for any point $\langle s,a \rangle$,the GP will report an upper confidence tail of $m(s) + 2\Sigma (s_{\tau+1})$ where $m$ and $\Sigma$ are defined in Section II-C. We modify GPQ to use these optimistic estimates in two ways: change value used in GP update to $\hat{Q}(s_i,a_i) = r(s_i) + \gamma \max_a [\hat{Q}(s_{i+1},a) + 2\Sigma(s,a)]$,and always take actions that are greedy with respect to the upper confidence tail.
The first change uses the upper tail of the next state's Q-value in the Bellman update to maintain optimism of the value function and is reminiscent of the backups performed in model-based interval estimation (38). The second change makes the algorithm select greedy actions with respect to an optimistic Q-function.
A degree of caution needs to be used when employing this optimistic strategy because of potentially slow convergence rates for GPQ when large amounts of data been collected. Once a large amount of data has been collected at a certain point,the confidence interval at that location can converge before GPQ has centered the mean around the true Q-value. These temporarily incorrect Q-values will still be optimistic and encourage exploration,but it may take a large amount of time for these points to converge to their true values,meaning this technique is prone to over-exploration. However,in many of our empirical tests,this variance-based exploration significantly outperformed $\epsilon$-greedy exploration.
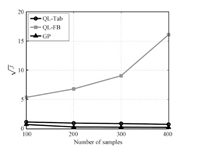
V. RESULTSOur experiments cover three domains,a discrete $5 \times 5$ Gridworld,a continuous state inverted pendulum (see (25)),and continuous state Puddle World[36]. Specific details of the domains are listed in Appendix C. These domains pose increasingly more difficult challenges to GPQ when choosing basis points. The algorithms compared in each domain include the two variants of online GPQ ($\epsilon$-greedy and optimistic),both using a budgeting scheme[14]. We also implemented a tabular Q-learner (QL-tab) using discretization,Q-learning with fixed-basis linear function approximation (QL-FB),and the GQ algorithm[4]. We chose these algorithms because they are off-policy and model-free online approaches for dealing with continuous state spaces. We report results for the best case parameter settings (see Appendix C) of 1) the learning rate (QL-tab,FA-FB,GQ),2) the exploration rate (QL-tab,FA-FB,GQ,GPQ-$\epsilon$-greedy),3) bandwidth of kernel (FA-FB,GQ,GPQ),4) the position of kernels (GQ,FA-FB,GPQ) and 5) the number of kernels (quantization level for QL-tab). After cross-validation,the policy learned from all these methods for the three domains are evaluated based on discounted cumulative reward averaged over $20$ independent runs and are shown in Fig. 2.

|
Download:
|
| Fig. 2. Average sum of discounted rewards for the experimental domains. The GQ and the QL variants are given more information because their bases are specified a priori, yet GPQ is able to reach comparable performance (often faster) while choosing its own basis functions. | |
The Gridworld consisted of $25$ cells,noisy transitions,and a goal reward of $1$ (step reward of $0$). While all of the algorithms find the optimal policy,the GPQ based methods converge much faster by quickly identifying important areas for basis points. We also see that optimistic exploration using the GP's variance is advantageous,as the algorithm very quickly uncovers the optimal policy.
The inverted pendulum is a continuous $2$-dimensional environment with the reward defined as the difference between the absolute value of the angle for two consecutive states. Again,GPQ quickly finds adequate bases and converges to a near optimal policy while GQ requires more samples. Q-learning with fixed bases and a tabular representation achieve adequate policies as well but require thousands of more samples. Optimistic exploration is not as helpful in this domain since the pendulum usually starts near the goal so targeted exploration is not required to find the goal region. Additional graphs in the appendix show that optimistic exploration is beneficial for certain parameter settings. The graphs in the appendix also demonstrate that GPQ methods are more resilient against small quantizations (budgets) because they are able to select their own bases,while GPQ and QL-FB are far more sensitive to the number and placement of bases.
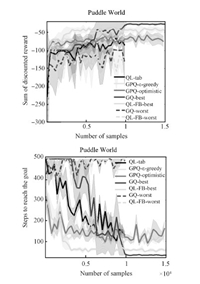
Finally,we performed experiments in the Puddle World domain,a continuous $2$-dimensional environment with Gaussian transition noise and a high-cost puddle between the agent and the goal. Because of the large range of values around the puddle,basis placement is more challenging here than in the other domains and GPQ sometimes converges to a cautious (puddle adverse) policy. Multiple lines are shown for QL-FB and GQ,depicting their best and worst case in terms of parameter settings,as they were extremely sensitive to these settings in this domain. Note that the best case versions of GQ and QL-FB reached better policies than GPQ,in the worst case,their Q-values appear to diverge. While this is not immediately evident from the discounted-reward graph,an additional graph in the appendix shows the average steps to the goal,which more clearly illustrates this divergence. While GQ has convergence guarantees when data comes from a fixed policy,those conditions are violated here,hence the potential for divergence. In summary,while very careful selection of parameters for QL-FB and GQ leads to slightly better performance,GPQ performs almost as well as their best case with less information (since it does not need the bases a priori) and far outperforms their worst-case results.
VI. CONCLUSIONSIn this paper,we presented a nonparametric Bayesian framework (GPQ) that uses GPs to approximate the value function in off-policy RL. We presented algorithms using this framework in the batch and online case and provided sufficient conditions for their convergence. We also described exploration scheme for the online case that made use of the GP's prediction confidence. Our empirical results show that GPQ's representational power allows it to perform as well or better than other off-policy RL algorithms. Our results from also reveal that a regularization-like term can help avoid in an application Thoerems 1 ~ 3 of off-policy approximate reinforcement learning employing Gaussian kernels. In future work,we plan to analyze the theoretical properties of our optimistic exploration scheme and deploy the algorithm on practical robotics platforms.
APPENDIX A SEQUENTIAL GP UPDATESPerforming batch prediction using GPs requires the inversion of a matrix that scales with the size of the data. Inverting this matrix at every iteration is computationally taxing,and many sparsification schemes have been proposed to reduce this burden[14, 31, 32]. In this paper,we use the sparsification method used in [14],which allows for sequential updates. The sparsification algorithm in [14] works by building a dictionary of basis points that adequately describe the input domain without including a basis point at the location of every observed data point.
Given a dictionary of bases,$Z_{d}$,the prediction and covariance equations are computed as
| \begin{align} m({z_{\tau + 1}}) = \alpha _t^{\rm{T}}k({Z_d},{z_{\tau + 1}}), \end{align} | (A1) |
| \begin{align} \Sigma ({z_{\tau + 1}}) = k({z_{\tau + 1}},{z_{\tau + 1}}) + {k^{\rm{T}}}({Z_d},{z_{\tau + 1}}){C_t}k({Z_d},{z_{\tau + 1}}), \end{align} | (A2) |
where $C=-(K+\omega^2I)^{-1}$,i.e.,$C$ is the negative of the inverse of the regularized covariance matrix which is computed recursively. A natural and simple way to determine whether to add a new point to the subspace is to check how well it is approximated by the elements in $\mathcal{Z}$. This is known as the kernel linear independence test[14],and has deep connections to reproducing kernel Hilbert spaces (RKHS)[5]. The linear independence test measures the length of the basis vector $\phi(z_{\tau+1})$ that is perpendicular to the linear subspace spanned by the current bases. For GPs,the linear independence test is computed as
| \[\begin{array}{*{20}{l}} {}&{{\beta _{\tau + 1}} = k({z_{\tau + 1}},{z_{\tau + 1}}) - }\\ {}&{\quad k{{({Z_d},{z_{\tau + 1}})}^{\rm{T}}}K{{({Z_d},{Z_d})}^{ - 1}}k({Z_d},{z_{\tau + 1}}),\;} \end{array}\] | (A3) |
when $\beta_{\tau+1}$ is larger than a specified threshold $\epsilon_{tol}$,then a new data point should be added to the dictionary. Otherwise,the associated weights $\alpha_\tau$ are updated,but the dimensionality of $\alpha_\tau$ remains the same. When incorporating a new data point into the GP model,the inverse kernel matrix and weights can be recomputed with a rank$-$1 update. To compute the updates in an online fashion,first define the scalar quantities
| \begin{align} & q^{(\tau+1)} =\notag\\ &\quad \frac{y-\alpha^{\rm T}_\tau k_{x_{\tau}}} {\omega_n^2 + k^{\rm T}(Z_d,z_{\tau+1})C_t k(Z_d,z_{\tau+1}) + k(z_\tau,z_\tau)}, \end{align} | (A4) |
| \begin{align} {r^{(\tau + 1)}} = {\rm{ - }}\frac{{\rm{1}}}{{\omega _{\rm{n}}^{\rm{2}}{\rm{ + }}{{\rm{k}}^{\rm{T}}}({{\rm{Z}}_{\rm{d}}},{{\rm{z}}_{\tau {\rm{ + 1}}}}){{\rm{C}}_{\rm{t}}}{\rm{k}}({{\rm{Z}}_{\rm{d}}},{{\rm{z}}_{\tau {\rm{ + 1}}}}){\rm{ + k}}({{\rm{z}}_\tau },{{\rm{z}}_\tau })}}. \end{align} | (A5) |
Let $e_{\tau+1}$ be the $(\tau+1)$ coordinate vector,and let $T_{\tau+1}(\cdot)$ and $U_{\tau+1}(\cdot)$ denote operators that extend a $\tau$-dimensional vector and matrix to a $(\tau+1)$ vector and $(\tau+1)\times (\tau+1)$ matrix by appending zeros to them,respectively. The GP parameters can be solved recursively by using
| \begin{align} \alpha_{\tau+1} &= T_{\tau+1}(\alpha_\tau) + q^{(\tau+1)}s_{\tau+1} ,\notag\\ C_{\tau+1} &= U_{\tau+1}(C_\tau) + r^{(\tau+1)}s_{\tau+1}s_{\tau+1}^{\rm T},\notag\\ s_{\tau+1} &= T_{\tau+1}(C_\tau k_{x_{\tau+1}}) + e_{\tau+1}. \end{align} | (A6) |
The inverse of the matrix $K(Z,Z)$,denoted by $P$,needed to solve for $\gamma_{\tau+1}$ is updated online through
| \begin{align} & P _{\tau+1} = \notag\\ &\quad U_{\tau+1}(P_{\tau}) + \gamma_{\tau+1}^{-1} \left(T_{\tau+1}(\hat{e}_{\tau+1})-e_{\tau+1}\right)\notag\\ &\quad \left(T_{\tau+1}(\hat{e}_{\tau+1})-e_{\tau+1}\right)^{\rm T}, \end{align} | (A7) |
where $\hat{e}_{\tau+1}:= P_\tau k(z_{\tau+1},Z_d)^{\rm T}$. In order to maintain a dictionary of fixed size,many point deletion criterion can be used[14]. Alternatively,[37] shows that if data is drawn from a Banach space and if $\epsilon_{tol} > 0$,then the number of points added to the dictionary will always be finite. If points are not deleted from the dictionary,the approximation error can be bounded analytically. In this paper,we consider a sparse representation of GPs without deletion of dictionary elements in order to facilitate analysis. Empirically,we have found that maintaining a fixed budget size does not significantly decrease performance.
APPENDIX B CONVERGENCE PROOFS A. Batch GP-TQETheorem 2. Given a GP with infinite data generated using a sparse approximation with acceptance tolerance $\beta_{tol}$,and given a Mercer kernel function that decays exponentially,there exists a finite regularization parameter $\omega_n^2$ such that the Bellman operator $T$ is a contraction in the batch setting.
Proof. We show that for a Mercer kernel that decays exponentially,there always exists a finite $\omega_n^2$ such that the Bellman operator results in a contraction in the supremum norm. For ease of exposition,all norms are assumed to be the infinity norm unless otherwise stated. Consider the Bellman operator
| \begin{align} &\|TQ(Z)-TP(Z)\|=\notag\\ &\quad \|K(Z,Z)(K(Z,Z) + \notag\\ &\quad\omega_n^2I)^{-1}(\gamma \vec Q(Z')-\gamma \vec P(Z'))\|\leq\notag\\ &\quad \gamma \|K(Z,Z)\| \| (K(Z,Z) +\notag\\ &\quad \omega_n^2I)^{-1}\| \|(Q(Z)-P(Z))\|. \end{align} | (A8) |
To bound $\|K(Z,Z)\| \| (K(Z,Z) + \omega_n^2I)^{-1}\| \leq 1$,first consider the norm of $\|K(Z,Z)\|$. By the structure of the kernel,we know
| \begin{align} \|K(Z,Z)\| = \max_j \sum_i k(z_j,z_i). \end{align} | (A9) |
We now argue that the norm of $K(Z,Z)$ is bounded for an infinite number of basis vectors selected using the linear independence test in (A9). The number of points that can be included in the basis vector set given the sparse selection procedure grows only polynomially as the volume of the input space increases. However,the kernel function decays exponentially fast as a function of distance. Therefore,as the volume of the input domain increases,the number of added kernels increases polynomially while the value they add to the sum (A10) decays exponentially fast. This means that the sum is convergent as the number of BV goes to infinity. We formalize this notion.
The following argument assumes a squared exponential kernel function $k(z_i,z_j) = \text{exp}(-\frac{1}{2}(z_i-z_j)^{\rm T}M (z_i-z_j))$,$M>0$. However,the results generalize to a variety of kernels that decay exponentially fast. Given some sparsity parameter $\beta_{tol}$,there exists an associated weighted distance $\delta_{tol}$ such that all points $z \in \mathcal{BV}$,$(z_i-z_j)^{\rm T}M (z_i-z_j) \geq \delta_{tol}^2$,$\forall i \neq j$. In particular,this bound can be computed as $\delta_{tol}^2 =-\text{ln}(1-\beta_{tol})$.
To compute $\delta_{tol}^2$,consider that the linear independence test $\beta_{z'} = k(z',z')-k(Z,z')^{\rm T} K(Z,Z)^{-1} k(Z,z')$ is also the conditional variance of the point $z'$ given {the exact values of the GP mean at locations $Z$ (the conditional variance with zero measurement noise)}. Conditional variance is a monotonically decreasing function as a function of number of basis vector points[38]. That is,given more observations,the conditional variance will never increase. Therefore,
| \begin{align} \beta_{z'} \leq& k(z',z')-k(z_i,z')^{\rm T} k(z_i,z_i)^{-1} k(z_i,z'),\quad \notag\\ & \forall i \leq1-\text{exp}(-\frac{1}{2}(z_i-z')^{\rm T}M (z_i-z'))^2. \end{align} | (A10) |
Therefore,if $\beta_{z'} \geq \beta_{tol}$,this implies $1-\text{exp}(-\frac{1}{2}(z_i-z')^{\rm T}M (z_i-z'))^2 \geq \beta_{tol}$,In order to bound a minimum weighted distance $(z_i-z_j)^{\rm T}M (z_i-z_j)$ between any two points such that both could be included in a sparse GP,
| \begin{align} \beta_{tol} = &1-\text{exp}(-\frac{1}{2}(z_i-z')^{\rm T}M (z_i-z'))^2 \nonumber\\ ((z_i-z')^{\rm T}M (z_i-z'))^2 = &-\text{ln}(1-\beta_{tol})\notag\\ \delta_{tol}^2 = &-\text{ln}(1-\beta_{tol}). \end{align} | (A11) |
This gives us a bound on how close any two points can be in a sparse GP. We now assume the worst case analysis that all points are as compact as possible while satisfying (A11). Given a volume in the input domain,distributing a maximal number of basis vectors is equivalent to performing a patterning operation with a lattice.
From Ehrhart's theory[39] ,we know that the number of lattice points in a polytope scales polynomially with the axis scaling factor,$t$,with maximum degree equal to the dimension of the space. In order to place an upper bound on (A9) to show convergence,we begin by considering the case of concentric hyperspheres of radii $n\delta_{tol}$,$n \in {\bf Z}$ around a basis vector location. Each hypersphere contains a number of lattice points that grows polynomially as some function $\mathcal{L}(n\delta_{tol})$. To conservatively estimate $\sum_i k(z_j,z_i)$,one can add the total number of lattice points contained in the interior of the hyperspere $n+1$,$\mathcal{L}((n+1)\delta_{tol})$,at the distance $n\delta_{tol}$. This estimate is conservative in two ways. First,all of the lattice points inside hypersphere $n$ are counted multiple times in the summation. Secondly,all of the lattice points at a distance between $[n\delta_{tol},(n+1)\delta_{tol}]$ are given weight at distance $(n\delta_{tol})$. Summing over all hyperspheres,we have for any $z_j$,
| \begin{align} &\sum_i k(z_j,z_i) \leq\notag\\ &\quad \sum_{n=1}^\infty f((n+1)\delta_{tol},{dim})\text{exp}(-(n\delta_{tol})^2), \end{align} | (A12) |
where $f((n+1)\delta_{tol},{dim})\text{exp}(-(n\delta_{tol})^2)$ is a polynomial function with highest degree dim. Substituting
| \begin{align} &\|K(Z,Z)\| \leq \notag\\ &\quad \sum_{n=1}^\infty f((n+1)\delta_{tol},{dim})\text{exp}(-(n\delta_{tol})^2), \end{align} | (A13) |
One can easily verify that the right side of (A13) converges by the integral test. Since $\|K(Z,Z)\|$ is finite,we know that there exists a finite $\omega_n^2$ that results in contraction for the Bellman operator.
B. Online GPQIn the following,we present a sufficient condition for convergence of online GPQ (see Section IV-A). The main idea is to show that the mean of the GP estimate of the Q-function,$\hat m$,converges to the mean $m^*$. Note that $m^*(z)={\pmb k}^{\rm T}(Z,z)\alpha^*$,where $\alpha^*$ is the unique minimizer of the regularized least squares cost function $\sum_t\|Q^*(z_t)-{\pmb k}^{\rm T}(Z,z_t)\alpha^*\|^2$. For ease of exposition,we define the following notation: $k(Z_t,z_t)={\pmb k}_t$,$K_t=K(Z_t,Z_t)$,and ${\pmb k}^\alpha_{t}\alpha_t=\max_{a'}({\pmb k}^{\rm T}(x_{t+1},a'))\alpha_t$. Similar to proofs of other online RL algorithms,including TD learning[18] and Q-learning[7],an ODE approach is used to establish stability[40]. The update in (15) is rewritten here for the case when the active basis set is fixed,that is,when $\beta_t\leq\beta_{tol}$
| \begin{align} &\alpha_{\tau+1} = \alpha_\tau + \zeta_\tau q^{(\tau+1)}(s_{\tau+1}),\notag \\ & C_{\tau+1} = (C_\tau) + \zeta_\tau r^{(\tau+1)}s_{\tau+1}s_{\tau+1}^{\rm T},\notag \\ & s_{\tau+1} = (C_\tau k_{x_{\tau+1}}), \end{align} | (A14) |
where $\hat s_{t+1}=C_t {\pmb k}_{t+1}+K_t^{-1} {\pmb k}_{t+1}$ and $\zeta_\tau$ is a decreasing sequence with $\sum_{\tau}\zeta_\tau=\infty$.
Theorem 4. For an ergodic sample obtaining policy $\pi$,and for each active basis set $\mathcal{BV}$,a sufficient condition for convergence with probability 1 of $\hat m(z_t)\to m^*(z_t)$ as $t \to \infty$ when using the online sparse GP algorithm of (A14) with the measurement model $\hat Q$ in (3) of the main paper is
| \begin{align} &{\rm E}_\pi\left[C_t {\pmb k}_t {\pmb k}^{\rm T}_t+K_t^{-1} {\pmb k}_t {\pmb k}^{\rm T}_t\right]\geq\notag\\ &\quad\gamma{\rm E}\left[C_t {\pmb k}_t {\pmb k}^\alpha_t+K_t^{-1} {\pmb k}_t {\pmb k}^\alpha_t\right]. \end{align} | (A15) |
Proof. Ensuring that assumptions required for Theorem 17 of [40] hold,the following ODE representation of the $\alpha$ update (A14) exists:
| \begin{align} \dot\alpha(t)={\rm E}_\pi\left[q_{t}S_{t}\right] \end{align} | (A16) |
In the following,it is shown that $\alpha\to\alpha^*$ for each active basis set. Let $\tilde \alpha=\alpha-\alpha^*$ and consider the continuously differentiable function $V(\tilde\alpha)=\frac{1}{2}\tilde {\alpha_t}^{\rm T}\tilde \alpha_t$. $V(\tilde\alpha_t)>0$ for all $\tilde \alpha_t\neq0$,therefore,$V$ is a Lyapunov like candidate function[41, 42]. The first derivative of $V$ along the trajectories of $\alpha(t)$ is
| \begin{align} & \dot V(\tilde\alpha)=\tilde\alpha_t^{\rm T}{\rm E}_\pi\Big[\frac{(C_t {\pmb k}_{t}+K_t^{-1} {\pmb k}_{t})}{\sigma^2_x}\times(r_t+\gamma {\pmb k}^\alpha_t\alpha_t-{\pmb k}_t^{\rm T}\alpha_t)\Big], \end{align} | (A17) |
where we have set $\sigma^2_x = \omega_n^2 + {\pmb k}^{\rm T}(Z,z)C_t {\pmb k}(Z,z') + {\pmb k}(z,z')$ for notational convenience. Note that $m^*(z)= {\pmb k}^{\rm T}(Z,z)\alpha^*$,and add and subtract ${\pmb k}_t^{\rm T}\alpha^*$ we have
| \begin{align} & \dot V(\tilde\alpha)=-\tilde\alpha_t^{\rm T}{\rm E}_\pi\Big[\frac{(C_t{\pmb k}_{t}+K_t^{-1}{\pmb k}_{t})}{\sigma^2_x} {\pmb k}_t^{\rm T}\tilde\alpha+\notag\\ &\quad \tilde\alpha^{\rm T}{\rm E}_\pi\left(\frac{(C_t {\pmb k}_{t}+K_t^{-1} {\pmb k}_{t})}{\sigma^2_x}\right) (r_t+\gamma {\pmb k}^\alpha_t\alpha_t-{\pmb k}_t^{\rm T}\alpha^*_t)\Big]. \end{align} | (A18) |
Adding and subtracting $\gamma {\pmb k}_t^{al^*}\alpha^*$,noting that ${\pmb k}^{al^*}_t\alpha^*\geq {\pmb k}^{\alpha}\alpha^*$,and $m^*_t=r_t+{\pmb k}^{\alpha^*}\alpha^*$ due to the Bellman equation,we have
| \begin{align} & \dot V(\tilde\alpha)= \notag\\ &\quad-\tilde\alpha_t^{\rm T}{\rm E}_\pi\Big[\frac{(C_t {\pmb k}_{t}+K_t^{-1} {\pmb k}_{t})}{\sigma^2_x}{\pmb k}_t^{\rm T}-\gamma\frac{(C_t{\pmb k}_{t}+K_t^{-1}{\pmb k}_{t})}{\sigma^2_x}{\pmb k}^\alpha_t\Big]\tilde{\alpha}. \end{align} | (A19) |
Hence,if the condition in (A15) is satisfied,$\dot V(\tilde\alpha)<0$ and $\alpha\to\alpha^*$ with probability 1 for each active basis set.
The argument above can be extended to show that $m(z)\to m^*(z)$ even if new bases are added to the active basis set. To see this,let $k$ be the time instant when a new basis is added and let $\alpha^*_{k+1}$ be the associated ideal weight vector. Note that the nature of the sparse GP algorithm ensures that $k+1\geq k+\Delta T$ with $\Delta T>0$. If $\Delta T$ is sufficiently large such that ${\rm E}_\pi (V(\alpha^*_{k+1})-V(\alpha^*_{k}))<0$ then the convergence is uniform across all bases.
APPENDIX C DETAILS OF EMPIRICAL RESULTSOur experiments cover three domains,discrete $5 \times 5$ Gridworld,a continuous state inverted pendulum (similar to [43]),and continuous state Puddle World[36]. The Gridworld consisted of $25$ cells with the agent always starting in the lower-left corner,a $0$ step cost,and a goal state in the upper-right corner with reward 1 and $\gamma =0.9$. Transitions were noisy with a 0.1 probability of the agent staying in its current location. We also performed experiments on the inverted pendulum,a continuous $2$-dimensional environment with three actions: applying forces of $-50$ N,$0$ N,or 50. The goal is to balance the pendulum upright within a threshold of $(-\pi/2,\pi/2)$ and the reward is defined as the difference between the absolute value of the angle for two consecutive states.
The Puddle World domain is a continuous $2$-dimensional environment with an agent moving in the four compass directions and Gaussian noise added to its movements. The initial state is at the bottom left of the domain and the goal region is near the top-right corner. The goal region and puddle placement follows the description of [36]. The "puddle" (which is really two overlapping puddles) between the agent and the goal causes negative reward proportional to the agent's distance to the center of each puddle. Steps outside of the puddle cause a reward of $-1$ except at the goal where the reward is $0$.
The results are influenced by several parameters,including 1) the learning rate (QL-tab,FA-FB,GQ),2) the exploration rate (QL-tab,FA-FB,GQ,GPQ-$\epsilon$-greedy),3) bandwidth of kernel (FA-FB,GQ,GPQ),4) the position of kernels (GQ,FA-FB,GPQ) and 5) the number of kernels (quantization level for QL-tab). The learning rate is set as $0.5/t^{\alpha}$ with $\alpha\in\{0.1,0.3,0.5\}$,the exploration rate is set according to $1/t^{\beta}$ with $\beta\in\{0.1,0.3,0.5\}$. For Gridworld the kernel budget is $25$; for Inverted Pendulum,the budget is chosen from $\{36,100\}$ and for Puddle World we use budgets from $\{100,400\}$. The quantization level for tabular Q-Learning is set the same as the budget for those function approximation methods. For each of the algorithms,the best combination of parameter settings was used for the figures in the main paper.
The following experiments from the inverted pendulum domain show the robustness of GPQ against changes in the quantization (budgeting) level and also the sensitivity of the fixed basis methods to the number of basis points. Fig. A2 demonstrates that GPQ methods are more resilient against small budgets because they are able to select their own bases,while GPQ and QL-FB are far more volatile. These graphs also show that optimistic exploration is beneficial for certain parameter settings.
|
Download:
|
| Fig. A1. The performance of GPQ with $\epsilon$-greedy exploration on Baird's counterexample (the "Star" problem) which can cause divergence with fixed-basis linear function approximation. | |

|
Download:
|
| Fig. A2. The performance for inverted pendulum under different budget (quantization levels), 36 (left) and 100 (right). GPQ is not sensitive to the quantization level because it selects its own bases, while the quantization level impacts the other algorithms significantly. For example, with higher a quantization level GQ converges slowly, and with a lower quantization level QL-tab performances poorly. | |
The graphs evaluating performance in Puddle World in Fig. A3 include an additional graph that shows the average steps to the goal,which more clearly illustrates the divergence of GQ and QL-FB. The divergence in these worst cases is caused by having many bases ($>$ 100) with overlapping bandwidths ($>$ 0.05). In contrast,a smaller number of bases with the same small bandwidth actually produces the best performances for these algorithms,because weights are updated almost independently. Fig. A4 elaborates on this sensitivity by showing the performance of all the algorithm under different budget (quantization) constraints with all other parameters fixed. We see GQ and QL-FB are very sensitive to the budget,and QL-tab is sensitive to the quantization level,while GPQ is relatively stable. In summary,while very careful selection of parameters for QL-FB and GQ leads to slightly better performance,GPQ performs almost as well as their best case with less information (since it does not need the bases a priori) and far outperforms their worst-case results.
|
Download:
|
| Fig. A3. The performance of the algorithms in Puddle World. The bandwidth is set to be 0.1 for the basis function in all methods. The number of basis (budget) is set to be 400. FA-FB and GQ diverge when the bases are placed uniformly over the state space. | |

|
Download:
|
| Fig. A4. The performance for Puddle World under different budget (quantization levels). | |
| [1] | Sutton R, Barto A. Reinforcement Learning, an Introduction. Cambridge, MA: MIT Press, 1998. |
| [2] | Engel Y, Mannor S, Meir R. Reinforcement learning with Gaussian processes. In: Proceedings of the 22nd International Conference on Machine learning. New York: ACM, 2005. 201-208 |
| [3] | Ernst D, Geurts P, Wehenkel L. Tree-based batch mode reinforcement learning. Journal of Machine Learning Research, 2005, 6: 503-556 |
| [4] | Maei H R, Szepesvári C, Bhatnagar S, Sutton R S. Toward off-policy learning control with function approximation. In: Proceedings of the 2010 International Conference on Machine Learning, Haifa, Israel, 2010. |
| [5] | Rasmussen C E, Williams C K I. Gaussian Processes for Machine Learning. Cambridge, MA: The MIT Press, 2006. |
| [6] | Engel Y, Szabo P, Volkinshtein D. Learning to control an octopus arm with gaussian process temporal difference methods. In: Advances in Neural Information Processing Systems 18. 2005. 347-354 |
| [7] | Melo F S, Meyn S P, Ribeiro M I. An analysis of reinforcement learning with function approximation. In: Proceedings of the 2008 International Conference on Machine Learning. New York: ACM, 2008. 664-671 |
| [8] | Deisenroth M P. Efficient Reinforcement Learning Using Gaussian Processes [Ph. D.dissertation], Karlsruhe Institute of Technology, Germany, 2010. |
| [9] | Jung T, Stone P. Gaussian processes for sample efficient reinforcement learning with rmax-like exploration. In: Proceedings of the 2012 European Conference on Machine Learning (ECML). 2012. 601-616 |
| [10] | Rasmussen C, Kuss M. Gaussian processes in reinforcement learning. In: Proceedings of the Advances in Neural Information Processing Systems, 2004, 751-759 |
| [11] | Kolter J Z, Ng A Y. Regularization and feature selection in leastsquares temporal difference learning. In: Proceedings of the 26th Annual International Conference on Machine Learning. New York: ACM, 2009. 521-528 |
| [12] | Liu B, Mahadevan S, Liu J. Regularized off-policy TD-learning. In: Proceddings of the Advances in Neural Information Processing Systems 25. Cambridge, MA: The MIT Press, 2012. 845-853 |
| [13] | Sutton R S, Maei H R, Precup D, Bhatnagar S, Silver D, Szepesvári C, Wiewiora E. Fast gradient-descent methods for temporal-difference learning with linear function approximation. In: Proceedings of the 26th Annual International Conference on Machine Learning. New York, USA: ACM, 2009. 993-1000 |
| [14] | Csat′o L, Opper M. Sparse on-line gaussian processes. Neural Computation, 2002, 14(3): 641-668 |
| [15] | Singh S P, Yee R C. An upper bound on the loss from approximate optimal-value functions. Machine Learning, 1994, 16(3): 227-233 |
| [16] | Watkins C J. Q-learning. Machine Learning, 1992, 8(3): 279-292 |
| [17] | Baird L C. Residual algorithms: reinforcement learning with function approximation. In: Proceedings of the 12th International Conference on Machine Learning. Morgan Kaufmann, 1995. 30-37 |
| [18] | Tsitsiklis J N, van Roy B. An analysis of temporal difference learning with function approximation. IEEE Transactions on Automatic Control, 1997, 42(5): 674-690 |
| [19] | Parr R, Painter-Wakefield C, Li L, Littman M L. Analyzing feature generation for value-function approximation. In: Proceedings of the 2007 International Conference on Machine Learning. New York: IEEE, 2007. 737-744 |
| [20] | Ormoneit D, Sen S. Kernel-based reinforcement learning. Machine Learning, 2002, 49(2-3): 161-178 |
| [21] | Farahmand A M, Ghavamzadeh M, Szepesvári C, Mannor S. Regularized fitted q-iteration for planning in continuous-space Markovian decision problems. In: Proceedings of the 2009 American Control Conference. St. Louis, MO: IEEE, 2009. 725-730 |
| [22] | Geist M, Pietquin O. Kalman temporal differences. Journal of Artificial Intelligence Research (JAIR), 2010, 39(1): 483-532 |
| [23] | Strehl A L, Littman M L. A theoretical analysis of model-based interval estimation. In: Proceedings of the 22nd International Conference on Machine Learning. New York: IEEE, 2005. 856-863 |
| [24] | Krause A, Guestrin C. Nonmyopic active learning of Gaussian processes: an exploration-exploitation approach. In: Proceedings of the 24th International Conference on Machine Learning. New York: IEEE, 2007. 449-456 |
| [25] | Desautels T, Krause A, Burdick J W. Parallelizing explorationexploitation tradeoffs with Gaussian process bandit optimization. In: Proceedings of the 29th International Conference on Machine Learning. ICML, 2012. 1191-1198 |
| [26] | Chung J J, Lawrance N R J, Sukkarieh S. Gaussian processes for informative exploration in reinforcement learning. In: Proceedings of the 2013 IEEE International Conference on Robotics and Automation. Karlsruhe: IEEE, 2013. 2633-2639 |
| [27] | Barreto A D M S, Precup D, Pineau J. Reinforcement learning using kernel-based stochastic factorization. In: Proceedings of the Advances in Neural Information Processing Systems 24. Cambridge, MA: The MIT Press, 2011. 720-728 |
| [28] | Chen X G, Gao Y, Wang R L. Online selective kernel-based temporal difference learning. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(12): 1944-1956 |
| [29] | Kveton B, Theocharous G. Kernel-based reinforcement learning on representative states. In: Proceedings of the 26th AAAI Conference on Artificial Intelligence. AAAI, 2012.977-983 |
| [30] | Xu X, Hu D W, Lu X C. Kernel-based least squares policy iteration for reinforcement learning. IEEE Transactions on Neural Networks, 2007, 18(4): 973-992 |
| [31] | Snelson E, Ghahramani Z. Sparse Gaussian processes using pseudoinputs. In: Proceedings of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2006. 1257-126 |
| [32] | Lázaro-Gredilla M, Quińonero-Candela J, Rasmussen C E, Figueiras- Vidal A R. Sparse spectrum gaussian process regression. The Journal of Machine Learning Research, 2010, 11: 1865-1881 |
| [33] | Varah J M. A lower bound for the smallest singular value of a matrix. Linear Algebra and Its Applications, 1975, 11(1): 3-5 |
| [34] | Lizotte D J. Convergent fitted value iteration with linear function approximation. In: Proceedings of the Advances in Neural Information Processing Systems 24. Cambridge, MA: The MIT Press, 2011. 2537-2545 |
| [35] | Kingravi H. Reduced-Set Models for Improving the Training and Execution Speed of Kernel Methods[Ph.D dissertation], Georgia Institute of Technology, Atlanta, GA, 2013 |
| [36] | Boyan J, Moore A. Generalization in reinforcement learning: Safely approximating the value function. In: Proceedings of the Advances in Neural Information Processing Systems 7. Cambridge, MA: The MIT Press, 1995. 369-376 |
| [37] | Engel Y, Mannor S, Meir R. The kernel recursive least-squares algorithm. IEEE Transactions on Signal Processing, 2004, 52(8): 2275-2285 |
| [38] | Krause A, Singh A, Guestrin C. Near-optimal sensor placements in gaussian processes: theory, efficient algorithms and empirical studies. The Journal of Machine Learning Research, 2008, 9: 235-284 |
| [39] | Ehrhart E. Geometrie diophantienne-sur les polyedres rationnels homothetiques an dimensions. Comptes rendus hebdomadaires des seances de l0academia des sciences, 1962, 254(4): 616 |
| [40] | Benveniste A, Priouret P, Métivier M. Adaptive Algorithms and Stochastic Approximations. New York: Springer-Verlag, 1990 |
| [41] | Haddad W M, Chellaboina V. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach. Princeton: Princeton University Press, 2008 |
| [42] | Khalil H K. Nonlinear Systems. New York: Macmillan, 2002. |
| [43] | Lagoudakis M G, Parr R. Least-squares policy iteration. Journal of Machine Learning Research (JMLR), 2003, 4: 1107-1149 |
 2014, Vol.1
2014, Vol.1 

