2. Tianjin Key Laboratory of Intelligent Robotics, Nankai University, Tianjin 300071, China;
3. College of Computer and Control Engineering, Nankai University, Tianjin 300071, China;
4. Tianjin Key Laboratory of Intelligent Robotics, Nankai University, Tianjin 300071, China;
5. College of Science, Civil Aviation University of China, Tianjin 300300, China
RECENTLY,distributive cooperative control of multi-agent systems,including unmanned underwater vehicles and multi-robot systems,has been a hot research topic in many fields, such as formation control[1, 2, 3],congestion control in communication systems,flocking[4, 5] and distributed sensor networks[6].
As a kind of consensus-associated problems[7, 8, 9, 10],formation control of multi-agent systems has been primarily investigated in many domains,such as unmanned air vehicles,cooperative transportation and surveillance. Compared with consensus issue, which requires the states of all agents to reach an agreement,the main objective of formation control is to design appropriate protocols that can make the agents achieve consensus of their states as well as preserve a desired geometrical shape with or without a group reference. There are many control methods raised to achieve the control targets,for instance,the leader-following approach[11, 12, 13],the behaviour based method[14, 15, 16],and the virtual architecture approach[17, 18].
Most existing work of formation control for multi-agent systems focuses on local rules using distributed sensing and controlling. In practice,some information of the agents in a multi-agent system,such as velocity,may not be obtained. For example,the agent may not be equipped with velocity sensors or the velocity measurement is not precise. Thus,the design of controller based on observers becomes a main trend in the research of multi-agent systems. Hong et al.[19, 20] studied the leader-follower consensus problem for multi-agent systems with an unknown velocity of variable leader,in which certain neighbour-based rules including distributed controller algorithm and observers were developed. In addition,many physical models in reality are nonlinear and have many uncertain terms. Several types of disturbance evaluating techniques are unknown input observer[21, 22],perturbation observer[23],disturbance observer[24, 25],and extended state observer (ESO)[26, 27, 28]. Different from other observers, ESO is designed distinctively to evaluate both extrinsic disturbance and inner uncertainty of the system itself. The total uncertain part is regarded as an augmented state which can be estimated via observer. ESO,working as an estimator,plays a key role in the active disturbance rejection control. Active disturbance rejection control (ADRC) was put forward based on ESO by Han in 1995,which was designed to estimate the total uncertainties on-line using ESO[26]. Besides,the nonlinear extended state observer could be simplified into a linear ADRC (LADRC) which is mainly discussed in this paper.
Motivated by the aforementioned statements,the formation control for a class of nonlinear multi-agent systems with a virtual leader to be tracked by followers is investigated in this paper. The followers respond to the virtual leader as they respond to their neighbours. We emphasize that there is no real leader among the followers. The introduction of a virtual leader increases robustness of the group in case of any single vehicle's failure. A distributed linear extended state observer (LESO) for second order multi-agent systems is proposed in the circumstance that velocities of an agent's neighbors cannot be measured. Furthermore,some local laws based on LESO are devised to track the active virtual leader,and the followers can shape the desired group formation by switching topology at the same time. The asymptotic stability for closed systems is guaranteed by a given model of the nonlinear couplings and the boundary of tracking error is obtained without a specific model of the plant.
The organization of this article is as follows. In Section Ⅱ,some preliminary knowledge is outlined. In Section Ⅲ,by designing a distributed control based on LESO,some sufficient conditions are proposed to ensure that the agents achieve the desired configuration with given or unknown nonlinear functions under the switching topology situation. Illustrative examples are presented to show validity of the theoretical results in Section Ⅳ,and the concluding statements are given in Section V.
Ⅱ. PRELIMINARIES AND PROBLEM FORMULATION A. NotationsWe first review some knowledge of graph theory and matrix analysis that we will use in the following sections. Consider a system containing one virtual leader and n agent-followers depicted by graph $\bar G.$ Graph $\bar G $ includes n followers,which are related to graph $G$,and a virtual leader, which sends information to some follower agents via directed edges. The graph $G(V,E,A)$ without self-loops is composed of the node set $V = \{ {v_1},\cdots ,{v_n}\} ,$ the edge set $E\in V \times V$,whose element is denoted by ${e_{ij}} = ({v_i},{v_j})$ ($i \ne j$),and the adjacency matrix $A = [{a_{ij}}]$ $(i,j = 1,2,\cdots ,n)$,where ${a_{ij}} > 0$ if $({v_i},{v_j}) \in E ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_{ij}} = 0$ if $({v_i},{v_j}) \notin E $ and ${a_{ii}} = 0.$ The Laplacian matrix associated with the graph is expressed as $L = D-A,$ where $D = [{d_{ij}}]$ is the diagonal degree matrix,with diagonal elements ${d_{ii}} = \sum_{j = 1}^n{{a_{ij}}} .$ The set of neighbours of agent i is denoted by ${N_i}(t) = \{ {v_j} \in V:{e_{ij}}{\rm{ = }}({v_i},{v_j}) \in E \} $ at time {\it t}. $B = {\rm diag}\{ {b_1},\cdots ,{b_n}\} $ is a diagonal matrix with the elements denoting the connection between the virtual leader and the follower agents,where ${b_i} > 0$ if the virtual leader is a neighbour of agent i,and otherwise, ${b_i} = 0$.
The maximal connected subgraph $ G_{1} $ induced from $ G $,is named as a component of $ G. $ We call graph $\bar{G} $ connected graph if at least one agent of each component of $ G $ is linked to the virtual leader via a directed edge.
In addition,to describe the variation of the relationship between agents,we define a piecewise-constant switching signal $\sigma :\left[{0,\infty } \right) \to { \Pi} = \{ 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} \cdots ,N\}.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} p = \sigma (t) \in { \Pi}$ switches in different time intervals $\left[{{t_j},{t_{j + 1}}} \right),$ where ${t_{j + 1}}-{t_j} \le {\tau _1}~( {\tau _1} > 0,~j = 0,1, \cdots ).$ The time intervals are bounded,nonoverlaying and continuous. Therefore, ${N_i}(t),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_{ij}}~(i,j = 1,2,\cdots ,n),$ ${L_p}$ and ${B_p}$ related with the switching interconnection graph ${\bar{G}_p}$ are time-varying $(p \in \Pi )$.
B. Linear Extended State Observer for Multi-agent Systems with Total UncertaintyWe consider a team of $n$ agents moving with a virtual leader operating in the same workspace.
The virtual leader is described as
| \begin{align} \left\{\begin{array}{lll} \dot{x_{0}}=v_{0},\,\,x_{0}\in {\bf R}^{m},\\ \dot{v_{0}}=u_{0},\,\,v_{0}\in {\bf R}^{m},\\ y=x_{0}, \end{array}\right. \end{align} | (1) |
where ${x_0},{v_0} \in {{\bf R}^m}$ are the virtual leader's position and velocity state,respectively. Input $u_{0}$ is known to all agents. The moving virtual leader we set is a known group reference to some followers representing a common interest of all the agents.
The following second-order system of $n$ agents is modeled as
| \begin{align} \left\{\begin{array}{lll} {{\dot x}_i} = {v_i},\\ {{\dot v}_i} = f({x_i},{v_i},\omega ) + {u_i},\end{array}\right. \end{align} | (2) |
where ${x_i},{v_i} \in {{\bf R}^m}$ are the position and velocity states of agent {$i$ } ($i$=1,2,$\cdots$,$n$),respectively. $f~({x_i},{v_i},\omega ) \in {{\bf R}^m}$ is a nonlinear function to portray the inner dynamics of agent i,where $\omega$ is exterior disturbance. ADRC is developed to deal with this problem. Presuming that f is differentiable,and setting
| \[z_i^{(1)} = {x_i},{\kern 1pt} {\kern 1pt} {\kern 1pt} z_i^{(2)} = {v_i},{\kern 1pt} {\kern 1pt} {\kern 1pt} z_i^{(3)} = f({x_i},{v_i},\omega ), {\kern 1pt} {\kern 1pt} {\kern 1pt} z_i^{(4)} = h({x_i},{v_i},\omega ),\] |
where $h = \dot f,$ we can rewrite (2) in an augmented state space form
| \begin{align} \left\{\begin{array}{lll} \dot z_i^{(1)} = z_i^{(2)},\\ \dot z_i^{(2)} = z_i^{(3)} + {u_i},\\ \dot z_i^{(3)} = h({z_i},\omega ),\\ {x_i} = z_i^{(1)}, \end{array}\right. \end{align} | (3) |
where ${z_i} = {(z_i^{(1){\rm T}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z_i^{(2){\rm T}}{\kern 1pt} {\kern 1pt} {\kern 1pt} z_i^{(3)^{\rm T}})^{\rm T}} \in {{\bf R}^{3m}}.$
Considering that f is an extended state in model (3),LESO for (3) is designed and the evaluation error of LESO is revealed in the next part.
Remark 1. In system (3), $f({x_i},{v_i},\omega )$ is the total uncertainty function which includes internal uncertain dynamics and external disturbance,and thus it is not easy to obtain the exact model of $f({x_i},{v_i},\omega )$. In the following section,the total uncertain part f will be seen as an augmented state,and can be estimated using the designed LESO.
C. Convergence of LESO1) Convergence of LESO with the given model of the plant: We first consider the case that the model of f is known.
The following decentralized LESO for (3) is proposed with the given function h,
| \begin{align} \left\{\begin{array}{lll} \dot{\hat{z}}_i^{(1)} = \hat z_i^{(2)} + {l_1}(z_i^{(1)}-\hat z_i^{(1)}),\\ \dot{\hat{z}}_i^{(2)} = \hat z_i^{(3)} + {l_2}(z_i^{(1)}-\hat z_i^{(1)}) + {u_i},\\ \dot{\hat{z}}_i^{(3)} = {l_3}(z_i^{(1)}-\hat z_i^{(1)}) + h({{\hat z}_i},\omega ), \end{array}\right. \end{align} | (4) |
where ${\hat z_i} = {(\hat z_i^{(1){\rm T}}{\kern 1pt} {\kern 1pt} \hat z_i^{(2){\rm T}}{\kern 1pt} {\kern 1pt} \hat z_i^{(3){\rm T}})} \in {{\bf R}^{3m}}$ is the observer outputs,$\hat z_i^{(1)}$ is the estimation of system output in system (3),$\hat z_i^{(2)}$ is used to evaluate the differential of system output, $\hat z_i^{(3)}$ is the extended state to estimate total disturbance {\it f},and ${l_k}~(k = 1,2,3)$ is the observer gain to be determined. In particular,we choose parameters as [29],that is,
| \begin{align} ({l_1},{l_2},{l_3}) = ({\omega _0}{\alpha _1},\omega _0^2{\alpha _2},\omega _0^3{\alpha _3}) \end{align} | (5) |
with ${\omega _0} > 0.$ Moreover,let the concrete characteristic polynomial of (4) be ${s^3} + {\alpha _1}{s^2} + {\alpha _2}s + {\alpha _3} = {(s + 1)^3}.$ Then we can choose parameters as [29],i.e.,${\alpha _k} = \frac{{\left( {n + 1} \right)!}}{{k!\left( {n + 1-k} \right)!}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (k = 1,2,3)$,so the characteristic polynomial is Hurwitz. Naturally,the characteristic polynomial of (4) is
| \begin{align} {\lambda _0}(s) = {(s + {\omega _0})^2}, \end{align} | (6) |
which makes $\omega_{0}$ turn out to be the only adjustable parameter of LESO.
Let $\tilde z_i^{(k)} = z_i^{(k)}-\hat z_i^{(k)}~(k = 1,2,3).$ From (3) and (4),we can get the observer estimation error as follows
| \begin{align} \left\{\begin{array}{lll} \dot{\tilde{z}}_i^{(1)} = \tilde z_i^{(2)}-{\omega _0}{\alpha _1}\tilde z_i^{(1)},\\ \dot{\tilde{z}}_i^{(2)} = \tilde z_i^{(3)}-\omega _0^2{\alpha _2}\tilde z_i^{(1)},\\ \dot{\tilde{z}}_i^{(3)} = h({z_i},\omega )-h({{\hat z}_i},\omega )-\omega _0^3{\alpha _3}\tilde z_i^{(1)}. \end{array}\right. \end{align} | (7) |
Now,let $\delta _i^{(k)} = \frac{{\tilde z_i^{(k)}}}{{\omega _0^{k-1}}}~(k = 1,2,3).$ Then (7) can be shown as
| \begin{align} {\dot \delta _i} = {\omega _0}{\Phi _1}{\delta _i} + {\Phi _2}\frac{{h({z_i},\omega )-h({{\hat z}_i},\omega )}}{{\omega _0^2}}, \end{align} | (8) |
where ${\delta _i} = {(\delta _i^{(1){\rm T}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta _i^{(2){\rm T}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta _i^{(3){\rm T}})} \in {{\bf R}^{3m}},$
| \[{\Phi _1} = \left( {\begin{array}{*{20}{c}} {-{\alpha _1}}&1&0\\ {-{\alpha _2}}&0&1\\ {-{\alpha _3}}&0&0 \end{array}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\Phi _2} = {(0{\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} 1)^{\rm T}},\] |
where ${\Phi _1}$ is Hurwitz according to the selection of ${\alpha _i}~(i = 1,2,3).$
Considering the above analysis,the following lemma quoted from [29] will be useful.
Lemma 1[29]. Assuming $h({z_i},\omega )$ is globally Lipschitz with respect to ${z_i},$ there exists a constant ${\omega _0} > 0,$ such that $\mathop {\lim }\limits_{t \to \infty } \tilde z_i^{(k)}(t) = 0{\kern 1pt} {\kern 1pt} (i = 1,2, \cdots ,n,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,2,3).$
Remark 2. In this subsection,LESO for system (3) is presented,where the model of f is completely known. Consequently,the derivative of function f is added in LESO (4).
Remark 3. Compared with the nonlinear extended state observer in [27] and other kinds of observers,$\omega _0$ turns out to be the only adjustable parameter of LESO according to (5). In addition,parameter $\omega _0$ can be determined by ${\omega _0} > 1 + {\left\| {P{\Phi _2}c'} \right\|^2},$ where $P$ is a positive definite matrix satisfying $\Phi _1^{\rm T}P + P{\Phi _1} =-I,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} c'$ is the Lipschitz constant related to $h$[29].
2) Convergence of LESO with the unknown function model: In this part,we will study the case that the nonlinear function including uncertainty,i.e.,the dynamics of plant $f$ is largely unknown. Different from (4),LESO in (4) now takes the form of
| \begin{align} \left\{\begin{array}{lll} \dot{\hat{z}}_i^{(1)} = \hat z_i^{(2)} + {l_1}(z_i^{(1)}-\hat z_i^{(1)}),\\ \dot{\hat{z}}_i^{(2)} = \hat z_i^{(3)} + {l_2}(z_i^{(1)}-\hat z_i^{(1)}) + {u_i},\\ \dot{\hat{z}}_i^{(3)} = {l_3}(z_i^{(1)}-\hat z_i^{(1)}). \end{array}\right. \end{align} | (9) |
The observer estimation error in (7) becomes
| \begin{align} \left\{\begin{array}{lll} \dot{\tilde{z}}_i^{(1)} = \tilde z_i^{(2)}-{\omega _0}{\alpha _1}\tilde z_i^{(1)},\\ \dot{\tilde{z}}_i^{(2)} = \tilde z_i^{(3)}-\omega _0^2{\alpha _2}\tilde z_i^{(1)},\\ \dot{\tilde{z}}_i^{(3)} = h({z_i},\omega )-\omega _0^3{\alpha _3}\tilde z_i^{(1)}, \end{array}\right. \end{align} | (10) |
and (8) can be expressed as
| \begin{align} {\dot \delta _i} = {\omega _0}{\Phi _1}{\delta _i} + {\Phi _2}\frac{{h({z_i},\omega )}}{{\omega _0^2}}. \end{align} | (11) |
Similar to the above analysis,we can get Lemma 2.
Lemma 2[29]. Assuming $h({z_i},\omega )$ is bounded, there exist a constant ${\sigma _i} > 0$ and a finite ${T_1} > 0$ such that $\left| {\tilde z_i^{(k)}(t)} \right| \le {\sigma _i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,\cdots ,n,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,2,3),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall {\kern 1pt} {\kern 1pt} t \ge {T_1} > 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\omega _0} > 0.$ Furthermore, \[{\sigma _i} = {\rm{O}}\left( {1/\omega _0^k} \right),\] for some positive integer $k$.
Remark 4. Different from the case that the model of plant is given in Section Ⅱ-C-1, LESO (9) for system (3) is presented in the face of unknown nonlinear function in Section Ⅱ-C-2. Therefore,the derivative of function $f$ does not appear in LESO (9).
Remark 5. What makes LESOs (4) and (9) different from other observers is that it is designed to estimate not only the state but also the comprehensive uncertainty by extended state $\hat z_i^{(3)}$ in (4) and (9). LESO needs the least information of the system plant. The above fact highlights the advantages of LESO.
Ⅲ. MAIN RESULTS A. ADRC for Multi-agent Systems with Given Model of PlantOur control goal here is to coordinate all the agents to achieve the prescribed spatial pattern,and to maintain the consistent pace of the virtual leader with the velocity of all agents converging to $v_{0}$,i.e.,$z_i^{(1)}-{x_0} \to {c_i},{\kern 1pt} {\kern 1pt} {\kern 1pt} z_i^{(2)} \to {v_0}$ as $t \to \infty ,$ where ${c_i}{\kern 1pt} {\kern 1pt} (i = 1,2,\cdots ,n)$ is the expected constant relative position vector between agent $i$ and the virtual leader.
With the assurance that our LESO is convergent,the LESO-based local law will have the form of
| \begin{align} {u_i} &=-{k_1}[\sum\limits_{j \in {N_i}(t)} {{a_{ij}} (\hat z_i^{(1)}-\hat z_j^{(1)}-{c_i} + {c_j}) + {b_i}(\hat z_i^{(1)}-{x_0}-{c_i})}]-\\ &\,\,\,\,{k_2}[\sum\limits_{j \in {N_i}(t)} {{a_{ij}}(\hat z_i^{(2)}-\hat z_j^{(2)})} + {b_i}(\hat z_i^{(2)}-{v_0})] + {u_0}-\hat z_i^{(3)}, \end{align} | (12) |
for $i = 1,2,\cdots ,n$,with constants ${k_1},{k_2} > 0$ to be determined,along with LESO (4).
The lemmas used in the proofs of the following theorems are given hare.
Consider
| \[\dot \vartheta (t) = W\vartheta (t) + y(t),\] |
where $\vartheta (t) = {({\vartheta _1} \,\cdots\,{\vartheta _n})^{\rm T}} \in {{\bf R}^n},{\kern 1pt} {\kern 1pt} y(t) = {({y_1} \,\cdots\,{y_n})^{\rm T}} \in {{\bf R}^n}$,and $W$ is an $n\times n$ matrix.
Lemma 3[29]. If $W$ is Hurwitz and $\mathop {\lim }\limits_{t \to \infty } \left\| {y(t)} \right\| = 0,$ then $\mathop {\lim }\limits_{t \to \infty } \left\| {\vartheta (t)} \right\| = 0.$
Lemma 4[19]. If graph ${\bar G_p},p \in {\Pi} = \{ 1,2, \cdots ,N\}$ is connected,then the symmetric matrix ${L_p} + {B_p}$ related with ${\bar G_p}$ is positive definite.
Considering system (3) and LESO (4),we have Theorem 1.
Theorem 1. Assuming that $h({z_i},\omega )$ is globally Lipschitz regarding to $z_i$,if the entire graph ${\bar G_p}$ $(p \in {\Pi} = \{ 1,2,\cdots ,N\})$ is connected in each time interval $\left[{{t_k},{t_{k + 1}}} \right),$ there exist constants ${\omega _0} > 0$ and ${k_1},{k_2} > 0,$ such that controller (12) with LESO (4) together yields
| \[\mathop {\lim }\limits_{t \to \infty } \left\| {z_i^{(1)}-{x_0}-{c_i}} \right\| = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {\lim }\limits_{t \to \infty } \left\| {z_i^{(2)}-{v_0}} \right\| = 0,\] |
namely,the agents can attain and preserve pre-described formation,and reach velocity consensus under arbitrary switching rule among the possible topologies.
Proof. $e_1$ and $e_2$ are set as
| \[\begin{array}{l} {e_1} = {(x_1^{\rm{T}}{\mkern 1mu} \cdots {\mkern 1mu} x_n^{\rm{T}})^{\rm{T}}} - {x_0}{\bf{1}} - {(c_1^{\rm{T}}{\mkern 1mu} \cdots {\mkern 1mu} c_n^{\rm{T}})^{\rm{T}}} = \\ {(z_1^{{{(1)}^{\rm{T}}}}{\mkern 1mu} \cdots {\mkern 1mu} z_n^{{{(1)}^{\rm{T}}}})^{\rm{T}}} - {x_0}{\bf{1}} - {(c_1^{\rm{T}}{\mkern 1mu} \cdots {\mkern 1mu} c_n^{\rm{T}})^{\rm{T}}},\\ {e_2} = {(v_1^{\rm{T}}{\mkern 1mu} \cdots {\mkern 1mu} v_n^{\rm{T}})^{\rm{T}}} - {v_0}{\bf{1}} = {(z_1^{{{(2)}^{\rm{T}}}}{\mkern 1mu} \cdots {\mkern 1mu} z_n^{{{(2)}^{\rm{T}}}})^{\rm{T}}} - {v_0}{\bf{1}}, \end{array}\] |
where ${\bf{1}} = {(1 \,\cdots\,1)^{\rm T}} \in {{\bf R}^n}.$ By using (3) and (4) we can get
| \begin{align} \left\{\begin{array}{lll} {{\dot e}_1} = {e_2},\\ {{\dot e}_2} =-{k_1}{{ H}_p}{e_1}-{k_2}{{ H}_p}{e_2} + {k_1}{{ H}_p}{{\tilde z}^{(1)}}{\rm{ + }}{k_2}{{ H}_p}{{\tilde z}^{(2)}} + {{\tilde z}^{(3)}}, \end{array}\right. \end{align} | (13) |
where ${{ H}_p} = ({L_p} + {B_p}) \otimes {I_m}.$
Let
| \[e = {({e_1^{\rm T}}{\kern 1pt} {\kern 1pt} {e_2^{\rm T}})^{\rm T}} \in {{\bf R}^{2nm}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde z = {({\tilde z^{(1)^{\rm T}}}{\kern 1pt} {\kern 1pt} {\tilde z^{(2)^{\rm T}}}{\kern 1pt} {\kern 1pt} {\tilde z^{(3)^{\rm T}}})^{\rm T}} \in {{\bf R}^{3nm}},\] |
where ${\tilde z^{(k)}} = {(\tilde z_1^{(k)^{\rm T}}\,\cdots\,\tilde z_n^{(k)^{\rm T}})^{\rm T}} \in {{\bf R}^{nm}},{\kern 1pt} {\kern 1pt} \tilde z_i^{(k)} = z_i^{(k)}- \hat z_i^{(k)}~(k = 1,2,3).$} It follows that
| \begin{align} {\dot e} = {{\Omega _e}e + {\Omega _{\tilde z}}\tilde z}, \end{align} | (14) |
where
| \[{\Omega _e} = \left( {\begin{array}{*{20}{c}} {{0_{nm}}}&{{I_{nm}}}\\ {-{k_1}{{ H}_p}}&{-{k_2}{{ H}_p}} \end{array}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\Omega _{\tilde z}} = \left( {\begin{array}{*{20}{c}} {{0_{nm}}}&{{0_{nm}}}&{{0_{nm}}}\\ {{k_1}{{ H}_p}}&{{k_2}{{ H}_p}}&{{I_{nm}}} \end{array}} \right).\] |
From Lemma 4,we get ${L_p} + {B_p}{\kern 1pt} {\kern 1pt} (p \in {\rm \Pi})$ is positive definite,then ${k_1},{k_2}$ can be selected such that ${\Omega _e}$ is Hurwitz.
Since $h({z_i},\omega )$ is globally Lipschitz with respect to ${z_i},$ we get from Lemma 1 that $\mathop {\lim }\limits_{t \to \infty } \left\| {{\Omega _{\tilde z}}\tilde z_i^{(k)}(t)} \right\| = 0.$ Since ${\Omega _e}$ is Hurwitz,from Lemma 1 and Lemma 3,we can choose constants ${\omega _0} > 0$ and ${k_1}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_2} > 0,$ such that $\mathop {\lim }\limits_{t \to \infty } {e_k}(t) = 0~ (k = 1,2).$ This completes the proof.
In the above theorem,the connected condition in each time interval $\left[{{t_k},{t_{k + 1}}} \right){\kern 1pt} {\kern 1pt} (k = 0,1,\cdots )$ is somehow strong. Then we will discuss the case with jointly connected condition.
Assume that in each interval $\left[{{t_k},{t_{k + 1}}} \right){\kern 1pt} {\kern 1pt} (k = 0,1,\cdots) $ there is a sequence of bounded,nonoverlapping subintervals
| \[[t_k^0,t_k^1),\cdots ,[t_k^j,t_k^{j + 1}),\cdots ,[t_k^{{l_k}-1},t_k^{{l_k}}), {\kern 1pt} {t_k} = t_k^0,{\kern 1pt} {\kern 1pt} {t_{k + 1}} = t_k^{{l_k}},\] |
where $t_k^{j + 1}-t_k^j \ge {\tau _2} > 0~(j = 0,1,\cdots ,{l_k}-1).$
The graph in each subinterval $[t_k^j,t_k^{j + 1})~(k = 0,1, \cdots ,\,j = 0,1,\cdots ,{l_k}-1)$ is fixed,allowed to be connected or disconnected. However,the graphs across interval $\left[{{t_k},{t_{k + 1}}} \right){\kern 1pt} {\kern 1pt} (k = 0,1,\cdots) $ are required to satisfy the following condition.
Assumption 1. The graphs over each time interval $\left[ {{t_k},{t_{k + 1}}} \right){\kern 1pt} {\kern 1pt} (k = 0,1, \cdots) $ are jointly connected.
We can know that matrix ${H_p} = {L_p} + {B_p}~(p \in {\Pi})$ has $n$ nonnegative eigenvalues related to graph ${\bar G_p},$ then we can get that the real part of the eigenvalues of ${\Omega _e}$ in (14) are nonpositive by selecting appropriate $k_{1}$ and $k_{2}.$ We label $\left\{ {\lambda _p^1,\cdots ,\lambda _p^{2n}} \right\}$ as the 2n eigenvalues of ${\Omega _e}.$ In addition,we define
| \[\lambda \left( p \right) = \left\{ {l~:~\lambda _p^l\neq 0,~l = 1,2,\cdots ,2n} \right\}.\] |
According to the above denotation,and by Lemma 5 in [30],we can derive that the graphs are jointly connected across $\left[ {{t_k},{t_{k + 1}}} \right){\kern 1pt} {\kern 1pt} (k = 0,1, \cdots) $,if and only if $\bigcup\nolimits_{t \in \left[ {{t_k},{t_{k + 1}}} \right)} {\lambda (\sigma (t)) = \left\{ {1, 2,\cdots ,2n} \right\}.} $
With the previous discussion,we will give the following theorem.
Theorem 2. With the assumption that $h({z_i},\omega )$ is globally Lipschitz regarding to $z_{i},$ if the interaction graph satisfies Assumption 1,then there exist constants $\omega_{0}>0$ and ${k_1},{k_2} > 0,$ such that controller (12) with LESO (4) together yields
| \[\mathop {\lim }\limits_{t \to \infty } \left\| {z_i^{(1)}-{x_0}-{c_i}} \right\| = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {\lim }\limits_{t \to \infty } \left\| {z_i^{(2)}-{v_0}} \right\| = 0,\] |
namely,the agents can attain and preserve desired formation,and reach velocity consensus.
Next,we will prove Theorem 2.
Proof. Consider the Lyapunov function $V(t) = {e^{\rm T}}(t)e(t)$ based on (14).
1) We will first show that ${\dot V} \le 0$. Without losing generality,we assume that the pth graph is active at time $t,$ then
| \[\begin{array}{l} \dot V(t) = {{\dot e}^{\rm{T}}}e + {e^{\rm{T}}}\dot e = \\ {e^{\rm{T}}}({\Omega _e}^{\rm{T}} + {\Omega _e})e + 2{e^{\rm{T}}}{\Omega _{\tilde z}}\tilde z. \end{array}\] |
By Lemma 1,we have that $\mathop {\lim }\limits_{t \to \infty } \tilde z = 0,$ then we can get
| \[{\dot V}(t) = {e^{\rm T}}({\Omega _e}^{\rm T} + {\Omega _e})e.\] |
Since ${\Omega _e}^{\rm T} + {\Omega _e}$ is symmetric and we label its 2$n$ nonpositive eigenvalues as $\mu (p) = \left\{ {\mu _p^1,\mu _p^2,\cdots ,\mu _p^{2n}} \right\},$ there exists an orthogonal matrix $W_{p}$ such that
| \[{W_p}({\Omega _e}^{\rm T} + {\Omega _e}){W_p}^{\rm T} = {\Lambda _p} = {\rm diag}\{ \mu _p^1,\mu _p^2,\cdots ,\mu _p^{2n}\}. \] |
Then we can obtain by translation $\bar e = {W_p}e,$
| \[\begin{array}{l} \dot V(t) = {{\bar e}^{\rm{T}}}{W_p}({\Omega _e}^{\rm{T}} + {\Omega _e}){W_p}^{\rm{T}}\bar e = {{\bar e}^{\rm{T}}}{\Lambda _p}\bar e = \\ \sum\limits_{i = 1}^{2n} {\mu _p^i\bar e_i^{\rm{T}}{{\bar e}_i}} \le \mu _p^{\max }\sum\limits_{i = 1}^{2n} {\bar e_i^{\rm{T}}{{\bar e}_i}} \le {\mu _m}\sum\limits_{i = 1}^{2n} {\bar e_i^{\rm{T}}{{\bar e}_i}} \le 0, \end{array}\] |
where $\mu _p^{\max } = \max \left\{ {\mu _p^1,\mu _p^2,\cdots ,\mu _p^{2n}} \right\},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\mu _m} = \mathop {\max }\limits_p \left\{ {\mu _p^{\max }} \right\}.$
Hence,$\mathop {\lim }\limits_{t \to \infty } V(t)$ exists.
2) Next,we want to show $\mathop {\lim }\limits_{t \to \infty } e(t) = 0$ by using Cauchy's convergence criteria.
For arbitrary $\varepsilon > 0,$ there exists a constant $K$ such that $\forall k \ge K,$
| \[\left| {\int_{{t_k}}^{{t_{k + 1}}} {\dot V(t){\rm d}t} } \right| = \left| {V({t_{k + 1}})-V({t_k})} \right| < \varepsilon .\] |
Then we have
| \[\begin{array}{l} \varepsilon > - \left[ {\int_{t_k^0}^{t_k^1} {\dot V(t){\rm{d}}t} + {\mkern 1mu} \cdots {\mkern 1mu} + \int_{t_k^{{l_k} - 1}}^{t_k^{{l_k}}} {\dot V(t){\rm{d}}t} } \right] \ge \\ - {\mu _m}[\int_{t_k^0}^{t_k^1} {\sum\limits_{i \in \lambda (\sigma (t_k^0))} {\bar e_i^{\rm{T}}{{\bar e}_i}} {\rm{d}}t} + {\mkern 1mu} \cdots {\mkern 1mu} + \\ \int_{t_k^{{l_k} - 1}}^{t_k^{{l_k}}} {\sum\limits_{i \in \lambda (\sigma (t_k^{{l_k} - 1}))} {\bar e_i^{\rm{T}}{{\bar e}_i}} {\rm{d}}t} ] > \\ - {\mu _m}[\int_{t_k^0}^{t_k^0 + {\tau _2}} {\sum\limits_{i \in \lambda (\sigma (t_k^0))} {\bar e_i^{\rm{T}}{{\bar e}_i}} {\rm{d}}t} + {\mkern 1mu} \cdots {\mkern 1mu} + \\ \int_{t_k^{{l_k} - 1}}^{t_k^{{l_k} - 1} + {\tau _2}} {\sum\limits_{i \in \lambda (\sigma (t_k^{{l_k} - 1}))} {\bar e_i^{\rm{T}}{{\bar e}_i}} {\rm{d}}t} ], \end{array}\] |
where $t_k^{i + 1}-t_k^i \ge {\tau _2} > 0{\kern 1pt} {\kern 1pt} (i = 0,1,\cdots ,{l_k}-1).$
Thus,for nonnegative integer $k > K{\kern 1pt} {\kern 1pt}$,we have
| \[-{\mu _m}\int_{t_k^i}^{t_k^i + {\tau _2}} {\sum\limits_{i \in \lambda (\sigma (t_k^i))} {\bar e_i^{\rm T}{{\bar e}_i}} {\rm d}t} < \varepsilon , {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 0,1,\cdots ,{l_k}-1.\] |
Thus,
| \[\begin{array}{l} \mathop {\lim }\limits_{t \to \infty } \int_t^{t + {\tau _2}} {[\sum\limits_{i \in \lambda (\sigma (t_k^0))} {\bar e_i^{\rm{T}}} (s){{\bar e}_i}(s) + {\mkern 1mu} \cdots {\mkern 1mu} } + \\ \sum\limits_{i \in \lambda (\sigma (t_k^{{l_k} - 1}))} {\bar e_i^{\rm{T}}} (s){{\bar e}_i}(s)]{\rm{d}}s = 0. \end{array}\] |
By Lemma 5 in [30] and the previous statements,we have $\bigcup\nolimits_{t \in [{t_k},{t_{k + 1}})} {\mu (\sigma (t))} = \{ 1,2,\cdots ,2n\} ,$ and consequently, $\mathop {\lim }\limits_{t \to \infty } \int_t^{t + {\tau _2}} {\left[{\sum\limits_{i = 1}^{2n} {{\beta _i}\bar e_i^{\rm T}(s){{\bar e}_i}(s)} } \right]} {\rm d}s = 0$,where ${\beta _i}~(i=1,2,\cdots,2n)$ are some positive integers.
In addition,from ${\dot V}(t) \le 0,$ we have $e(t)$ and $\dot{e}(t)$ are bounded,and thus $\sum\limits_{i = 1}^{2n} {{\beta_i}\bar e_i^{\rm T}(s){{\bar e}_i}(s)} $ is uniformly continuous,then we can get by the Barbalat's lemma that
| \[\mathop {\lim }\limits_{t \to \infty } {e_i}(t) = 0,{\kern 1pt} {\kern 1pt} i = 1,2,\cdots ,2n.\] |
From 1) and 2),the proof is completed.
Remark 6. It should be noted that the formation control problem in Theorem 1 is studied with the condition that the graphs in each interval $\left[{{t_k},{t_{k + 1}}} \right)$ are connected,which is somehow strong,while switching between all the possible topologies is random without restriction. However,in Theorem 2,we relax the condition to jointly connected graphs across $\left[{{t_k},{t_{k + 1}}} \right)$,which imposes certain requirements on designing the rule of switching among the possible topologies.
B. ADRC for Multi-agent Systems with Function Model Mostly UnknownIn the following,we investigate the problem without detailed model of nonlinear function by LESO (9).
Theorem 3. With the assumption that $h({z_i},w)$ is bounded,if the entire graph ${\bar G_p}~(p \in {\Pi} = \{ 1,2, \cdots ,N\} )$ is connected in each time interval $\left[ {{t_k},{t_{k + 1}}} \right)$,there exist constants ${\xi _i} > 0,{\kern 1pt} {\kern 1pt} {\omega _0} > 0$ and ${k_1},{k_2} > 0$ such that controller (12) with LESO (9) together yields
| $$\left| {{e_i}(t)} \right| \le {\xi _i},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,\cdots ,2nm,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall t \ge {T_3} > 0,$$ |
namely,the tracking error is bounded.
Proof. Solving (14),we get
| \begin{align} e(t) = {{\rm e}^{{\Omega _e}t}}e(0) + \int_0^t {{{\rm e}^{{\Omega _e}(t-\tau )}}{\Omega _{\tilde z}}\tilde z(\tau ){\rm d}\tau }. \end{align} | (15) |
From (14) and Lemma 2,we can get for any $t \geq T_1$,
| \begin{align} \begin{array}{l} {\left( {{\Omega _{\tilde z}}\tilde z(t)} \right)_{i = 1,\cdots ,nm}} = 0,\\ \left| {{{\left( {{\Omega _{\tilde z}}\tilde z(t)} \right)}_{i = nm + 1,\cdots ,2nm}}} \right| \le \left\| {{\Omega _{\tilde z}}} \right\|{\sigma _i} = {\gamma _0}. \end{array} \end{align} | (16) |
Similar to Theorem 1,we choose appropriate $k_{1}$ and $k_{2}$ such that ${\Omega _e}$ is Hurwitz,and set $\Psi = {(0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\gamma _0})^{\rm T}}$ and $\varphi (t) = \int_0^t {{{\rm e}^{{\Omega _e}(t-\tau )}}{\Omega _{\tilde z}}} \tilde z(\tau ){\rm d}\tau ,$ where
| \begin{align} \left| {{\varphi _i}(t)} \right| \le \left| {{{(\Omega _e^{- 1}\Psi )}_i}} \right| + \left| {{{(\Omega _e^{-1}{{\rm e}^{{\Omega _e}t}}\Psi )}_i}} \right| \end{align} | (17) |
is the ith element of $\varphi (t),$ and
| \begin{align} \begin{array}{l} {\left. {\left| {{{(\Omega _e^{-1}\Psi )}_i}} \right|} \right|_{i = 1,2,\cdots ,nm}} \le {\gamma _1}({\gamma _0}),\\ {\left. {\left| {{{(\Omega _e^{-1}\Psi )}_i}} \right|} \right|_{i = nm + 1,\cdots ,2nm}} = 0. \end{array} \end{align} | (18) |
Since ${\Omega _e}$ is Hurwitz,we have
| \begin{align} \left| {{{\left( {{{\rm e}^{{\Omega _e}t}}} \right)}_{ij}}} \right| \le {\gamma _2}, \end{align} | (19) |
for $t \ge {T_2},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i,j = 1,2,\cdots ,2nm.$ Let ${T_3} = \max \left\{ {{T_1},{T_2}} \right\}.$ It follows that
| \begin{align} \left| {{{({{\rm e}^{{\Omega _e}t}}\Psi )}_i}} \right| \le {\gamma _2}{\gamma _0}, \end{align} | (20) |
for $t \ge {T_3},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,\cdots ,2nm,$ and
| \begin{align} \left| {{{(\Omega _e^{-1}{{\rm e}^{{\Omega _e}t}}\Psi )}_i}} \right| \le \left\{ {\begin{array}{*{20}{c}} {{{\left. {\left| {{{\left( {{\Omega _e}} \right)}_i}} \right|{\gamma _2}{\gamma _0}} \right|}_{i = 1,2,\cdots ,nm,}}}\\ {{{\left. {{\gamma _2}{\gamma _0}} \right|}_{i = nm + 1,\cdots ,2nm,}}} \end{array}} \right. \end{align} | (21) |
for $t \ge {T_3}.$ According to (17),(18) and (21),we have
| \begin{align} \left| {{\varphi _i}(t)} \right| \le \left\{ \begin{array}{l} {\left. {{\gamma _1}({\gamma _0}) + \left| {{{\left( {{\Omega _e}} \right)}_i}} \right|{\gamma _2}{\gamma _0}} \right|_{i = 1,2,\cdots ,nm,}}\\ {\left. {{\gamma _2}{\gamma _0}} \right|_{i = nm + 1,\cdots ,2nm,}} \end{array} \right. \end{align} | (22) |
for all $t \ge {T_3}.$ Let ${e_{sum}}(0) = \left| {{e_1}(0)} \right| + \left| {{e_2}(0)} \right| + \,\cdots\,+ \left| {{e_{2nm}}(0)} \right|.$ The following inequality is obtained
| \begin{align} \left| {{{\left( {{{\rm e}^{{\Omega _e}t}}e(0)} \right)}_i}} \right| \le {\gamma _2}{e_{sum}}(0), \end{align} | (23) |
for $t \ge {T_3},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,\cdots ,2nm.$ From (15),it follows that
| \begin{align} \left| {{e_i}(t)} \right| \le \left| {{{\left( {{{\rm e}^{{\Omega _e}t}}e(0)} \right)}_i}} \right| + \left| {{\varphi _i}(t)} \right|. \end{align} | (24) |
According to (15),(22)$\sim$(24),we have
| \begin{align} \left| {{e_i}(t)} \right| &\leq \left\{ {\begin{array}{*{20}{c}} {{{\left. {\!\!\!\!{\gamma _2}{e_{sum}}(0) + {\gamma _1}({\gamma _0}) + \left| {{{\left( {{\Omega _e}} \right)}_i}} \right|{\gamma _2}{\gamma _0}} \right|}_{i = 1,2,\cdots ,nm}}}\\ {{{\left. {{\gamma _2}{\gamma _0}} \right|}_{i = nm + 1,\cdots ,2nm}}} \end{array}} \right.\!\!\! \leq{\xi _i}, \end{align} | (25) |
for $t \ge {T_3},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,\cdots ,2nm,$ where
| $${\xi _i} = \max \left\{ {{\gamma _2}{e_{sum}}(0) + {\gamma _1}({\gamma _0}) + \left| {{{\left( {{\Omega _e}} \right)}_i}} \right|{\gamma _2}{\gamma _0},{\gamma _2}{\gamma _0}} \right\}.$$ |
This completes the proof.
Remark 7. In Section Ⅲ-A,ADRC based on LESO (4) is put forward for the exact model of the plant which is completely known. Differently,in Section Ⅲ-B,ADRC based on LESO (9) is designed when the nonlinear uncertain function model is mostly unknown.
Remark 8. Since the strong estimation and compensation ability,ADRC based on LESO is widely applied due to its marvellous merits,especially in engineering projects.
1) In practice,the uncertainties are usually derived from two sources,internal uncertainty (including parameter and structure uncertainty) and external disturbance. There are many control methods aiming at these two issues,such as proportion integration differentiation (PID),robust control and disturbance observer. However,owning to less dependence on system model,as the estimation mechanism in ADRC,LESO is used to not only estimate all the system states but also evaluate the total uncertainty online.
2) According to real-time estimated values as stated in 1) above, ADRC can compensate the internal and external disturbance actively.
In sum,ADRC method,which depends on less information of system model,can estimate and offset the total uncertainty coming from internal and external disturbance. Combining with the distributed control idea,it has the advantage of strong robustness against many kinds of uncertainty.
Ⅳ. NUMERICAL SIMULATIONSIn the rest of the paper,numerical simulations are given to verify effectiveness of the protocols proposed above.
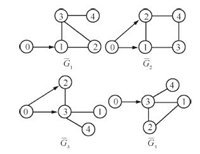
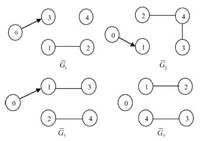
A multi-agent system with four followers and a virtual leader in a two-dimensional space is studied. Four possible variable topologies of the multi-agent system are depicted in Fig. 1. The network starts with topology ${\bar G_1}$ and switches to another topology randomly chosen within $\{ {\bar G_1},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar G_2},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar G_3},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar G_4}\} $ at time $T_{i}$ ($i=1,2,\cdots$),with the switching time $T_{i}$ satisfying mod\,$(T_i,eps)\leq$0.1 $(eps$ is chosen within [1,1.5]).
|
Download:
|
| Fig. 1. Four possible network topologies associated with graphs ${\bar G_p}{\kern 1pt} {\kern 1pt} (p = 1,2,3,4)$. | |
Case 1(a). The multi-agent system with the given plant model satisfies the conditions of Theorem 1 and the topologies are shown in Fig. 1. Here,
| \[\begin{array}{l} {u_0} = {\left( {\sin (t)\quad 0} \right)^{\rm{T}}},f( \cdot ) = {\left( {\sin ({x_{11}})\quad \sin ({x_{12}})} \right)^{\rm{T}}} + \omega ,\\ \omega = {\left( {0.3\sin ({x_{11}})\quad 0.1\sin ({x_{12}})} \right)^{\rm{T}}},{x_1} = {({x_{11}}\quad {x_{12}})^{\rm{T}}}. \end{array}\] |
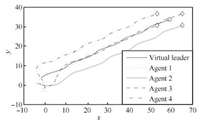
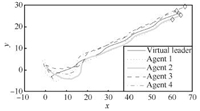
We choose ${c_1} = {(-6\quad-3)^{\rm T}},{c_2} = {(6\quad- 3)^{\rm T}},{c_3} = {(6\quad 3)^{\rm T}},{c_4} = {(-6\quad 3)^{\rm T}},$ ${\omega _0} = 8$ and $ {k_1} = {k_2} = 1.$ The original positions are chosen within $[-5, 5]$ at random,the initial velocities are \[{v_1} = {v_2} = {v_3} = {v_4}{(0.1\quad 0.1)^{\rm{T}}}.\] It can be easily verified that the conditions of Theorem 1 are satisfied. The position errors and the velocity errors of simulation results are shown in Figs. 2$\sim$6,respectively. We can see that the followers have achieved the desired formation and velocity consensus has been reached,where the final positions of the followers and the virtual leader are marked by '$\diamond$' and 'o',respectively, in Fig. 2. Fig. 2 shows that the followers asymptotically form the pre-described formation and reach velocity consensus.
|
Download:
|
| Fig. 2. Trajectories of agents in Case 1(a). | |
Fig. 3 shows that the relative distances between the virtual leader and follower $i~( i=1,2,3,4)$ are
| \[{c_1} = {(-6\quad-3)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_2} = {(6\quad-3)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {c_3} = {\kern 1pt} {\kern 1pt} {(6\quad 3)^{\rm T}},{\kern 1pt} {\kern 1pt} {c_4} = {\kern 1pt} {(-6\quad 3)^{\rm T}}.\] |
|
Download:
|
| Fig. 3. Trajectories of relative distance between the virtual leader and follower $i~ (i=1,2,3,4)$ in Case 1(a). | |
|
Download:
|
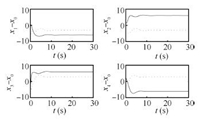
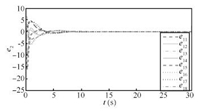
| Fig. 4. Trajectories of position errors ${e_1}$ in Case 1(a). | |
|
Download:
|
| Fig. 5. Trajectories of velocity errors ${e_2}$ in Case 1(a). | |
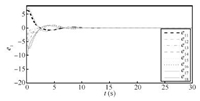
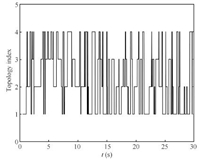
In Fig. 6,the network starts with topology ${\bar G_1}$ and switches to another topology randomly chosen within $\{ {\bar G_1},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar G_2},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar G_3},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar G_4}\} $ at time $T_i\,(i=1,2,\cdots)$ with the switching time $T_{i}$ satisfying mod$(T_i,eps)\leq0.1$ ($eps$ is chosen within [1,1.5]).
|
Download:
|
| Fig. 6. Random switching among 4 possible topologies in Case 1(a). | |
Case 1(b). The multi-agent system with the given plant model satisfies the conditions of Theorem 2,and we use the same parameters as in Case 1(a). Four possible topologies of the multi-agent system are shown in Fig. 7.
|
Download:
|
| Fig. 7. Four possible network topologies associated with graphs ${\bar G_p}~(p = 1,2,3,4)$ in Case 1(b). | |
The possible topology graphs are switched as ${\bar G_1} \to {\bar G_2} \to {\bar G_3} \to {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar G_4} \to {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar G_1} \to {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar G_2} \to \cdots .$ We set ${t_{k + 1}}-{t_k} =$ 1s and each graph is active for 0.5s in the interval $\left[{{\kern 1pt} {t_k},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {t_{k + 1}}} \right)$. Here,we choose ${c_1} = {(-3\quad-3)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_2} = {(1\quad- 1)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {c_3} = {\kern 1pt} {\kern 1pt} {(3 \quad 3)^{\rm T}},{\kern 1pt} {\kern 1pt} {c_4} = {\kern 1pt} {(-1 \quad 1)^{\rm T}},$ and ${k_1} = {k_2} = 5.$
From Fig. 7,we can see that graphs ${\bar G_1} \cup {\bar G_2}$ and ${\bar G_3} \cup {\bar G_4}$ are connected,which satisfies the conditions of Theorem 2. The initial states are chosen randomly. Then the followers have achieved the desired formation and reached velocity consensus,as shown in Figs. 8$\sim$12.
|
Download:
|
| Fig. 8. Trajectories of agents in Case 1(b). | |
|
Download:
|
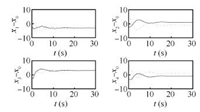
| Fig. 9. Trajectories of relative distance between the virtual leader and follower $i\,(i=1,2,3,4)$ in Case 1(b). | |
|
Download:
|
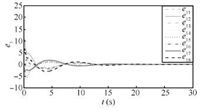
| Fig. 10. Trajectories of position errors $e_{1}$ in Case 1(b). | |
|
Download:
|
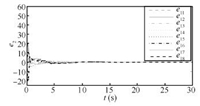
| Fig. 11. Trajectories of velocity errors $e_{2}$ in Case 1(b). | |
|
Download:
|
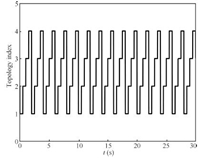
| Fig. 12. Designed switching signal among 4 possible topologies in Case 1(b). | |
Case 2(a). The formation control for multi-agent system with plant dynamics largely unknown is studied in this case where the observer bandwidth ${\omega _0} = 8.$
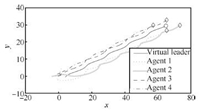
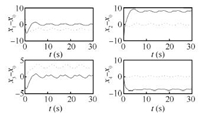
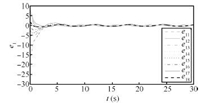
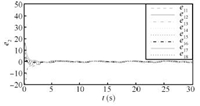
We use the same parameters as Case 1 and the topologies used are shown in Fig. 1. Then we can choose ${c_1} = {(0\quad-3)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_2} = {(8\quad 0)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_3} = {\kern 1pt} {\kern 1pt} {\kern 1pt} {(0\quad 3)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_4} = {\kern 1pt} {\kern 1pt} {\kern 1pt} {(-8\quad 0)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\omega _0} = 8,$ and ${k_1} = {k_2} = 1.$ Thus it is easy to show that the conditions of Theorem 2 are satisfied. The simulation-based results presented in Figs. 13$\sim$16 show that the tracking error is bounded with LESO (9).
|
Download:
|
| Fig. 13. Trajectories of agents in Case 2(a). | |
|
Download:
|
| Fig. 14. Trajectories of relative distance between the virtual leader and follower $i\,(i=1,2,3,4)$ in Case 2(a). | |
|
Download:
|
| Fig. 15. Trajectories of position errors $e_{1}$ in Case 2(a). | |
|
Download:
|
| Fig. 16. Trajectories of velocity errors $e_{2}$ in Case 2(a). | |
Case 2(b). The formation control for multi-agent system with plant dynamics largely unknown is investigated in this part where the observer bandwidth ${\omega _0} = 50.$
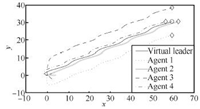
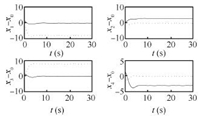
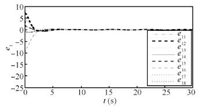
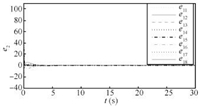
The topologies used are shown in Fig. 1. We choose ${c_1} = {(0\quad-8)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_2} = {(3\quad 0)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_3} = {\kern 1pt} {\kern 1pt} {(0\quad 8)^{\rm T}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_4} = {\kern 1pt} {(-3\quad 0)^{\rm T}},$ and ${\omega _0} = 50,$ then we can see that the follower agents can form the desired formation and the tracking error will be decreased in Figs. 17$\sim$20.
|
Download:
|
| Fig. 17. Trajectories of agents with ${\omega _0} = 50$ in Case 2(b). | |
|
Download:
|
| Fig. 18. Trajectories of relative distance between the virtual leader and follower $i\,(i=1,2,3,4)$ with ${\omega _0} = 50$ in Case 2(b). | |
Comparison between Figs. 15,16 and Figs. 19,20 demonstrates that if the parameter is selected appropriately,the tracking errors will be decreased.
Ⅴ. CONCLUSIONThe paper investigated formation control for a class of nonlinear multi-agent systems with a virtual leader. Based on LESO,an active disturbance rejection control is developed that can make the followers achieve and preserve the desired formation under two situations. The sufficient condition is that the graph is connected with the given nonlinear function,which is then relaxed to the case that the graphs are jointly connected. However,in the face of large model uncertainties,the tracking errors are shown to be bounded. For some condition restrictions,it is somehow difficult to apply the jointly connected condition to the model with large uncertainty,thus further research will be considered in future. Finally,simulation examples are provided.
|
Download:
|
| Fig. 19. Trajectories of position errors $e_{1}$ with ${\omega _0} = 50$ in Case 2(b). | |
|
Download:
|
| Fig. 20. Trajectories of velocity errors $e_{2}$ with ${\omega _0} = 50$ in Case 2(b). | |
The authors acknowledge Mingwei Sun for the valuable suggestions on the theory and application of active disturbance rejection control (ADRC) and the anonymous reviewers.
| [1] | Zheng Jun, Yan Wen-Jun. A distributed formation control algorithm and stability analysis. Acta Automatica Sinica, 2008, 34(9):1107-1113(in Chinese) |
| [2] | Xiao F, Wang L, Chen J, Gao Y P. Finite-time formation control for multi-agent systems. Automatica, 2009, 45(11):2605-2611 |
| [3] | Chen F, Chen Z Q, Liu Z X, Xiang L Y, Yuan Z Z. Decentralized formation control of mobile agents:a unified framework. Physica A:Statistical Mechanics and its Applications, 2008, 387(19-20):4917-4926 |
| [4] | Wen G H, Duan Z S, Li Z K, Chen G R. Flocking of multi-agent dynamical systems with intermittent nonlinear velocity measurements. International Journal of Robust and Nonlinear Control, 2012, 22(16):1790-1805 |
| [5] | Chen Z Y, Zhang H T. Analysis of joint connectivity condition for multiagents with boundary constraints. IEEE Transactions on Cybernetics, 2013, 43(2):437-444 |
| [6] | Tu Zhi-Liang, Wang Qiang, Shen Yi. A distributed simultaneous optimization algorithm for tracking and monitoring of moving target in mobile sensor networks. Acta Automatica Sinica, 2012, 38(3):452-461(in Chinese) |
| [7] | Yan J, Guan X P, Luo X Y, Yang X. Consensus and trajectory planning with input constraints for multi-agent systems. Acta Automatica Sinica, 2012, 38(7):1074-1082 |
| [8] | Su Y F, Huang J. Cooperative output regulation of linear multi-agent systems by output feedback. Systems and Control Letters, 2012, 61(12):1248-1253 |
| [9] | Li Z K, Liu X D, Ren W, Xie L H. Distributed tracking control for linear multiagent systems with a leader of bounded unknown input. IEEE Transactions on Automatic Control, 2013, 58(2):518-523 |
| [10] | Ren W. Consensus based formation control strategies for multi-vehicle systems. In:Proceedings of the American Control Conference. Minneapolis, MN:IEEE, 2006. 4237-4242 |
| [11] | Dong Y, Huang J. Leader-following rendezvous with connectivity preservation of a class of multi-agent systems. In:Proceedings of the 201231st Chinese Control Conference (CCC). Hefei, China:IEEE, 2012. 6477-6482 |
| [12] | Qin W, Liu Z X, Chen Z Q. Impulsive formation control algorithms for leader-following second-order nonlinear multi-agent systems. In:Proceedings of the 13th IFAC Symposium on Large Scale Complex Systems:Theory and Applications. Shanghai, China:IFAC, 2013. 172-177 |
| [13] | Wang J L, Wu H N. Leader-following formation control of multi-agent systems under fixed and switching topologies. International Journal of Control, 2012, 85(6):695-705 |
| [14] | Arkin R C. Behavior-Based Robotics. Cambridge, MA:MIT Press, 1998 |
| [15] | Balch T, Arkin R C. Behavior-based formation control for multirobot teams. IEEE Transactions on Robotics and Automation, 1998, 14(6):926-939 |
| [16] | Lumelsky V J, Harinarayan K R. Decentralized motion planning for multiple mobile robots:The cocktail party model. Autonomous Robots, 1997, 4(1):121-135 |
| [17] | Lewis M A, Tan K H. High precision formation control of mobile robots using virtual structures. Autonomous Robots, 1997, 4(4):387-403 |
| [18] | Hernandez-Martinez E G, Aranda Bricaire E. Non-collision conditions in multi-agent virtual leader-based formation control. International Journal of Advanced Robotic Systems, 2012, 9:100 |
| [19] | Hong Y G, Hu J P, Gao L X. Tracking control for multi-agent consensus with an active leader and variable topology. Robotics and Autonomous Systems, 2006, 42(7):1177-1182 |
| [20] | Hong Y, Chen G R, Bushnell L. Distributed observers design for leaderfollowing control of multi-agent. Automatica, 2008, 44(3):846-850 |
| [21] | Basile G, Marro G. On the observability of linear, time-invariant systems with unknown inputs. Journal of Optimization Theory and Applications, 1969, 2(6):410-415 |
| [22] | Chen J, Patton R J, Zhang H Y. Design of unknown input observers and robust fault detection filters. International Journal of Control, 1995, 63(1):85-105 |
| [23] | Kwon S, Chung W K. Combined synthesis of state estimator and perturbation observer. ASME Journal of Dynamic Systems, Measurement, and Control, 2003, 125(1):19-26 |
| [24] | Yang H Y, Guo L, Han C. Tracking trajectory of heterogenous multiagent systems with disturbance observer based control. In:Proceedings of the 201210th World Congress on Intelligent Control and Automation (WCICA). Beijing, China:IEEE, 2012. 2352-2357 |
| [25] | Yang H Y, Guo L, Zou H L. Robust consensus of multi-agent systems with time-delays and exogenous disturbances. International Journal of Control, Automation and Systems, 2012, 10(4):797-805 |
| [26] | Han Jing-Qing. A class of extended state observers for uncertain systems. Control and Decision, 1995, 10(1):85-88(in Chinese) |
| [27] | Gao Z Q, Han Y, Huang Y Q. An alternative paradigm for control system design. Decision and Control, 2001. In:Proceedings of the 40th IEEE Conference on Decision and Control. Orlando, FL:IEEE, 2001. 5:4578-4585 |
| [28] | Gao Z Q. Scaling and bandwidth-parameterization based controller tuning. In:Proceedings of the 2003 American Control Conference. Denver, USA:IEEE, 2003. 6:4989-4996 |
| [29] | Zheng Q, Gao L Q, Gao Z Q. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In:Proceedings of the 200746th IEEE Conference on Decision and Control. New Orleans, LA:IEEE, 2007. 3501-3506 |
| [30] | Ni W, Cheng D Z. Leader-following consensus of multi-agent systems under fixed and switching topologies. Systems and Control Letters, 2010, 59(3-4):209-217 |
 2014, Vol.1
2014, Vol.1 


