2. Optimization and Systems Theory, Royal Institute of Technology, Stockholm 10044, Sweden;
3. School of Control Science and Engineering, Shandong University, Jinan 250061, China
Actuator saturation is one of the most common and important nonlinearities existing in practical control systems since the capability of any physical actuator is limited. If its adverse effect is neglected,actuator saturation can not only result in performance degradation of the closed-loop system,but also become the source of instability. For this reason, considerable attention has been paid to control systems with actuator saturation since 1950s and many significant results have been proposed in the last decade[1, 2, 3, 4, 5, 6, 7, 8].
It is well-known that if a linear system is asymptotically null controllable with bounded controls (ANCBC),low-gain feedback is an effective methodology that can be used to achieve semi-global results[2, 9, 10]. Low-gain feedback refers to a family of stabilizing state feedback gains,parameterized in a scalar,which tends to zero as the parameter approaches zero. Based on low-gain feedback design,an enhanced design method,referred to as the low-and-high-gain feedback depending on the low-gain parameter $\varepsilon$ and the high-gain parameter $\rho$,was also developed in [9, 11] to achieve closed-loop performances beyond large stability region,including robust semi-global stabilization and disturbance rejection.
In recent years,research on behaviors of multi-agent systems has received extensive attention,mainly due to its applications in the formation control of unmanned air vehicles,the cooperative control of mobile robots,the design of distributed sensor networks,and so on[12, 13, 14]. In collective behaviors of multiple agents,the leader-follower problem is one of the important coordination problems in the studies of mobile agents, where the leader may be a real leader (such as a target,an evader,and a pre-defined position),or a virtual leader (such as a reference trajectory or a specified path). The leader has the desired trajectory or target,which can help guide the whole group. The other agents follow the leader using the relative information obtained from their neighbors and the leader. This is also known as cooperative tracking control[15], synchronization to a leader,pining control[16],or model reference consensus[17].
In literature,much attention has been paid to the leader-follower problem of first-order or second-order integrator dynamics[15, 18, 19]. For example,Jadbabaie et al.[18] demonstrated that a simple neighbor rule makes all agents eventually move in the same direction despite the absence of centralized coordination and each agent$'$s set of neighbors changing with time as the system evolves under a joint connection condition. In [19],to reach a consensus,the connectivity keeping problem was considered by computing the ratio of the numbers of leaders and followers. In practice,some state variables of agents (or even their leaders) may not be measured. In this case, decentralized observer design is needed for each agent. Hong et al.[15] proposed a neighbor-based observer to estimate the unmeasurable variables (velocity) of an active leader. Moreover, they extended the result to the second-order case[20].
Despite much work in these two areas,little attention except [21, 22, 23, 24] has been paid to multi-agent systems with constraints. In practice,general linear multi-agent systems are more interesting,and include the integrator dynamics (of any order) as a special case. However,there are few results except [23, 24, 25] on this kind of multi-agent systems,since it is not an easy work to study such systems. Particularly,there are,to our best knowledge,fewer results based on parametric algebraic Ricatti equations for general linear ANCBC multi-agent systems subject to actuator saturation.
The objective of this paper is to investigate the tracking problem of leader-follower multi-agent systems subject to actuator saturation. For ANCBC agents,a new family of scheduled low-and-high-gain feedback controllers are constructed to achieve semi-global leader-following consensus by tuning related parameters. Such control laws rely on the asymptotical property of a class of parametric algebraic Ricatti equations. The dynamics of each agent studied can be of any order,the communication topology within the multi-agent systems is fixed and represented by an undirected graph. We show that if the associated undirected graph of the system is connected,with the proposed control law,all the followers can semi-globally track the leader eventually. An illustrative example with simulations shows that low-and-high-gain-based method as well as control protocols is effective for the tracking problem of the leader-follower multi-agent systems with actuator saturation.
The remainder of this paper is organized as follows. Section II provides necessary preliminaries and problem formulation. Section III presents the main results of this paper. An example is given in Section IV to verify the theoretical analysis,which is followed by the conclusion in Section V.
II. PRELIMINARIESA.Notations
Some mathematical notations are used throughout this paper. ${\bf R}^n$ denotes the $n$-dimensional Euclidean space. For $y=(y_1,y_2, \cdots,y_n)^{\rm T}\in {\bf R}^n$, $\|y\|_\infty=\max\{|y_i|,1\le i\le n\}$,and $\|\cdot\|$ represents the Eulidean norm. $si gn(\cdot)$ stands for the symbol function. Let $I_n\in{\bf R}^{n\times n}$ be the identity matrix. ${\bf 1}_n\in{\bf R}^{n}$ is the vector with all entries being one,and $0$ denotes a zero value or a zero matrix with appropriate dimension. In a symmetric matrix,the symbol "$\ast$" is used to denote the term that is induced by symmetry. Wherever the dimensions of the matrices are not mentioned,they are assumed to be of compatible dimensions. $A=[a_{ij}]$ is a matrix with $a_{ij}$ being the entry of $i$-th row and $j$-th column,$A$ $=$ ${\rm diag}\{a_{i}\}$ is a diagonal matrix with diagonal entries $a_i$,and $A^{\rm T}$ is the transpose of matrix A. tr$(W)$ denotes the trace of $W$,and Kronecker product is denoted by "$\otimes$".
B.Graph Theory
We use a graph to represent the communication topology among agents. An undirected graph $\mathcal{G}=(\mathcal{V}, \mathcal{E},\mathcal{A})$ of order $N$ consists of a vertex set $\mathcal{V}=\{1,2,\cdots,N\}$,an edge set $\mathcal{E}$ $=(i,j): i,j\in\mathcal{V}\times\mathcal{V}$ and a weighted adjacency matrix $\mathcal{A}=$ $[a_{ij}]$ $\in$ ${\bf R}^{N\times N}$,where $a_{ii}=0$,and $a_{ij}=a_{ji}\ge0$. $a_{ij}$ $>$ $0$ if and only if there is an edge between vertex $i$ and vertex $j$ and the two vertices are called adjacent (or they are mutual neighbors). The set of neighbors of vertex $i$ is denoted by $\mathcal{N}_i$ $=$ $\{j\in\mathcal{V}: (i,j)\in\mathcal{E},j\neq i\}$.
A path of length $l$ from vertex $v_i$ to vertex $v_j$ is a sequence of $l + 1$ distinct vertices starting from $v_i$ and ending at $v_j$ such that the consecutive vertices are adjacent. For an undirected graph $\mathcal{G}$,if there is a path between any two vertices,then $\mathcal{G}$ is called connected, otherwise,disconnected. For the leader-following system,we consider another graph $\bar{\mathcal{G}}$ associated with the system consisting of $n$ agents (which are called followers) and one leader denoted by $x_l$. %A subgraph $\mathcal{G}_1$ of graph $\mathcal{G}$ is an induced %subgraph if two vertices in $\mathcal{G}_1$ are adjacent if and only %if they are adjacent in $\mathcal{G}$. An maximal connected induced %subgraph of $\mathcal{G}$ is called a component of $\mathcal{G}$.
Throughout this paper,we assume that the graph is unweighted,
that is,$\mathcal{A}$ is a 0-1 matrix. Let $|\mathcal{N}_i|$ be
the cardinality of the set $\mathcal{N}_i$,and define the
Laplacian $L$ corresponding to the undirected graph $\mathcal{G}$
as
\begin{align}\label{eq m.1} L=[l_{ij}]_{N\times N},~~~\mbox{
where}~~l_{ij}=\left\{\begin{array}{ll} \mid\mathcal{N}_i\mid,&
i=j,\\
-1,& j\in\mathcal{N}_i,\\
0,&\mbox{ otherwise.}\end{array}\right.
\end{align}
(1)
By the definition,for an undirected graph,$L$ is symmetric and every row sum of it is zero. $0$ is an eigenvalue of $L$ and ${\bf 1}_N$ is the associated eigenvector,that is,$L{\bf 1}_N=0$. If $\mathcal{G}$ is connected,then $0$ is the algebraically simple eigenvalue of $L$ and all the other eigenvalues are positive.
C.Problem Formulation
In this paper,we consider an input saturated multi-agent system consisting of $N$ followers and one leader which can be described by a graph $\bar{\mathcal{G}}$. It contains $N$ agents (related to graph $\mathcal{G}$) and a leader with directed edges from some agents to the leader Graph $\bar{\mathcal{G}}$ is said to be connected if at least one agent in each component of graph $\mathcal{G}$ is connected to the leader by a directed edge. In addition,we define $G$ $=$ ${\rm diag}\{g_1,g_2,\cdots,g_N\}$ as the leader adjacency matrix associated with graph $\bar{\mathcal{G}}$,where $g_i>0$ if agent $i$ is adjacent to the leader and otherwise $g_i=0$.
Consider a system with $N$ agents,and the dynamics of each agent
is
\begin{align}
\dot x^i=Ax^i+B{\rm sat}(u^i),~~~i\in\mathcal{N},
\end{align}
(2)
\begin{align}
\dot x_l=Ax_l,
\end{align}
(3)
The following assumption, lemma,and definition are necessary in the development of this paper.
${\bf Assumption 1.}$ The pair $(A,B)$ is controllable,and all the eigenvalues of $A$ are in the closed left half complex plane, which is equivalent to the ANCBC of system (2) with the leader (3).
${\bf Lemma 1}$[8]. Let $Q:[0,1] \rightarrow{\bf R}^{n\times n}$: be a
continuously differentiable matrix-valued function such that
$Q(0)=0$,and $({\rm d}Q(\varepsilon)/{\rm d}\varepsilon)>0$ for
any $\varepsilon\in(0,1]$. Also,let Assumption 1 be satisfied.
Then,the continuous-time algebraic Riccati equation defined as
\begin{align}
A^{\rm T}P+PA-PBB^{\rm T}P+Q(\varepsilon)=0
\end{align}
(4)
1) For any $\varepsilon\in(0,1]$,$P(\varepsilon)$ makes $A-BB^{\rm T}P(\varepsilon)$ be Hurwitz-stable;
2) $\lim_{\varepsilon\rightarrow{0^+}}P(\varepsilon)=0$;
3) $P(\varepsilon)$ is continuously differentiable with respect to $\varepsilon$ and \begin{align*} \frac{{\rm d} P(\varepsilon)}{{\rm d}\varepsilon}>0,~~~\forall \varepsilon\in(0,1]. \end{align*}
For the positive definite solution $P(\varepsilon)\in{\bf
R}^{n\times n},~ \varepsilon\in(0,1]$ of (4),and a positive
scalar $\xi$,let $\Omega(P(\varepsilon),\xi)$ represent the
following ellipsoid:
\begin{align} \Omega(P(\varepsilon),
\xi)=\left\{x^i\in{\bf R}^n:~{x^i}^{\rm T}P(\varepsilon)x^i\le
\xi,~i\in\mathcal{N}\right\}.
\end{align}
(5)
${\bf Lemma 2.}$ Define the sets $\Theta(P(\varepsilon))=\{x\in{\bf R}^n:$ $x^{\rm T}P(\varepsilon)x\cdot {\rm tr}(B^{\rm T}P(\varepsilon)B)\le 1\}$, and $\mathcal{L}(B^{\rm T}P(\varepsilon))=\{x\in{\bf R}^n:$ $\parallel B^{\rm T}P(\varepsilon) x\parallel_\infty\le1\}$; then,for $\forall x\in{\bf R}^n$,we have $\Theta(P(\varepsilon))\subset\mathcal{L}(B^{\rm T}P(\varepsilon))$, where $P(\varepsilon),~\varepsilon\in(0,1]$ is the positive definite solution of the Riccati equation (4).
${\bf Proof.}$ Since $P(\varepsilon)$ is positive definite,we have
$P(\varepsilon)=W^{\rm T}W$ for some nonsingular $W$. Then
\begin{align}
& \parallel B^{\rm T}P(\varepsilon)
x\parallel_\infty^2\le\parallel
B^{\rm T}P(\varepsilon)x\parallel^2=x^{\rm T}P(\varepsilon)BB^{\rm T}P(\varepsilon)x=\notag\\
&\qquad (Wx)^{\rm T}WBB^{\rm T}W^{\rm T}(Wx)\le\notag\\
&\qquad {\rm tr}(WBB^{\rm T}W^{\rm T})\Vert Wx\Vert^2.
\end{align}
(6)
${\bf Lemma 3}$[15]. If graph $\bar{\mathcal{G}}$ is connected,then the symmetric matrix $H=L+G$ associated with $\bar{\mathcal{G}}$ is positive definite.
${\bf Definition 1.}$ For system (2) and any given arbitrarily
large bounded set $\mathcal{X}\in{\bf R}^n$,if for any initial
$x^i(0)\in\mathcal{X}\subset\Omega(P(\varepsilon),\xi)$ defined in
(5) such that
\begin{align}
\lim_{t\rightarrow\infty}\parallel
x^i(t)-x_l(t)\parallel=0,~~i\in\mathcal{N}\end{align}
(7)
In this section,we would like to extend the low-and-high-gain design methods introduced earlier by Lin and Saberi and their coworkers[9, 11] for linear systems with actuator saturation to the tracking control of leader-follower multi-agent systems subject to actuator saturation,and propose a new family of scheduled low-and-high-gain control protocols that can be used to solve the tracking problem of system (2).
A.Scheduled Low-and-high-gain Feedback Design
For system (2),it is assumed that only a subset of agents have
access to model (3). In this case,the information available to
follower $i$ is given by
\begin{align}
{\zeta}^i={\displaystyle\sum_{j\in\mathcal{N}_i}}a_{ij}(x^i-x^j)+g_i(x^i-x_l),
\end{align}
(8)
\begin{align}
\left\{\begin{array}{*{20}l}
\!\dot v^i=(A-BB^{\rm T}P(\varepsilon))v^i-B{\rm sat}((1+\rho)B^{\rm T}P(\varepsilon)(\delta^i-{\zeta}^i)),\\
\!u_i=(1+\rho)B^{\rm T}P(\varepsilon)(\delta^i-{\zeta}^i),\end{array}\right.
\end{align}
(9)
\begin{align}
\delta^i={\displaystyle\sum_{j\in\mathcal{N}_i}}a_{ij}(v^i-v^j)+g_iv^i,
\end{align}
(10)
Remark 1. For the multi-agent systems with fixed and connected topology,the low-gain parameter $\varepsilon$ solely controls the domain of synchronization $\Omega(P(\varepsilon),\xi)$ defined in Definition 1,i.e.,by tuning the parameter $\varepsilon$,one can control the size of the domain of synchronization; the smaller parameter $\varepsilon$,the larger the domain of synchronization. On the other hand,although the high-gain parameter $\rho$ does not affect the domain of synchronization,it can be used in improving the tracking rate of system (2) (see Example 1).
With the control law (9),the tracking problem of leader-follower is said to be solved if \begin{align*} x^i(t)\rightarrow x_l(t),~~ \forall i\in\mathcal{N},~~\mbox{\rm as} ~~t\rightarrow\infty. \end{align*}
B.Tracking Control with Low-and-high-gain Feedback
Let $x_e^i=x^i-x_l$ and $v_e^i=v^i$,then associating with (2),
(3) and protocol (9),we have the error closed-loop system
\begin{align}
\left\{\begin{array}{*{20}l}
\dot x_e^i =&\!\!\!\! Ax_e^i+B{\rm sat}\Big((1+\rho)B^{\rm
T}P(\varepsilon) \times \\
&\!\!\!\!
\Big[{\displaystyle\sum_{j\in\mathcal{N}_i}}a_{ij}((v_e^i-v_e^j)-(x_e^i-x_e^j))+g_i(v_e^i-x_e^i)\Big]\Big),\\[4mm]
\dot v_e^i =&\!\!\!\!(A-BB^{\rm T}P(\varepsilon))v_e^i-B{\rm sat}\Big((1+\rho)B^{\rm
T}P(\varepsilon) \times\\
&\!\!\!\!
\Big[{\displaystyle\sum_{j\in\mathcal{N}_i}}a_{ij}((v_e^i-v_e^j)-(x_e^i-x_e^j))+g_i(v_e^i-x_e^i)\Big]\Big).
\end{array}\right.
\end{align}
(11)
\begin{align}
\eta_i={\displaystyle\sum_{j\in\mathcal{N}_i}}a_{ij}[(v_e^i-v_e^j)-(x_e^i-x_e^j)]+g_i(v_e^i-x_e^i).
\end{align}
(12)
\begin{align}
\eta=(H\otimes I_n)(v_e-x_e),
\end{align}
(13)
\begin{align}
\left\{\begin{array}{*{20}l}
\dot x_e=&\!\!\!\!(I_N\otimes A)x_e-(I_N\otimes B)
{\rm sat}\Big(\Big[(I_N \otimes \\&\!\!\!\!(1+\rho)B^{\rm T}P(\varepsilon))
(H\otimes I_n)\Big](x_e-v_e)\Big),\\[2mm]
\dot v_e=&\!\!\!\!(I_N\otimes(A-BB^{\rm T}P(\varepsilon)))v_e+(I_N\otimes B){\rm sat}\Big(
\Big[(I_N \otimes\\
&\!\!\!\!(1+\rho)B^{\rm T}P(\varepsilon))(H\otimes
I_n)\Big](x_e-v_e)\Big).
\end{array}\right.
\end{align}
(14)
\begin{align}
THT^{\rm T}=D={\rm
diag}\{\lambda_1,\lambda_2,\cdots,\lambda_N\}
\end{align}
(15)
Now,by the orthogonal transformation
\begin{align}
\tilde{x}_e=(T\otimes I_n)x_e,~~\tilde{v}_e=(T\otimes
I_n)v_e,
\end{align}
(16)
\begin{align}
\left\{\begin{array}{*{20}l}
\dot{\tilde{x}}_e=&\!\!\!\!(I_N\otimes A)\tilde{x}_e-
(I_N\otimes B)
{\rm sat}\Big(\Big[(I_N \otimes\\&\!\!\!\! (1+\rho)B^{\rm T}P(\varepsilon))
(D\otimes I_n)\Big](\tilde{x}_e-\tilde{v}_e)\Big),\\[2mm]
\dot{\tilde v}_e=&\!\!\!\!(I_N\otimes(A-BB^{\rm T}P(\varepsilon)))\tilde v_e+
(I_N\otimes B){\rm sat}\Big(\Big[(I_N \otimes\\
&\!\!\!\!(1+\rho)B^{\rm T}P(\varepsilon))(D\otimes
I_n)\Big](\tilde{x}_e-\tilde{v}_e)\Big).
\end{array}\right.
\end{align}
(17)
\begin{align}
\left[\begin{array}{*{20}c}
\dot{\tilde{x}}_e^i\\
\dot{\tilde{v}}_e^i\\
\end{array}\right]=\left[\begin{array}{*{20}cc}
A&\;~~0\\
0&\;~~A-BB^{\rm T}P(\varepsilon)\\
\end{array}\right]\left[\begin{array}{*{20}cc}
\tilde{x}_e^i\\
\tilde{v}_e^i\\
\end{array}\right]-\left[\begin{array}{*{20}c}
B\\
-B\\
\end{array}\right]\times\notag\\
{\rm sat}\Big(\lambda_i(1+\rho)\left[\begin{array}{*{20}c}
B^{\rm T}P(\varepsilon)&\;~
-B^{\rm T}P(\varepsilon)\\
\end{array}\right]\left[\begin{array}{*{20}c}
\tilde{x}_e^i\\
\tilde{v}_e^i\\
\end{array}\right]\Big).
\end{align}
(18)
Obviously,if the adjacent graph $\bar{\mathcal{G}}$ is connected, the tracking problem can be solved if and only if system (18) is simultaneously asymptotically stable for $i=1,2,\cdots,N$,where $P(\varepsilon)$,$\varepsilon\in(0,1]$ is the positive definite solution of the Riccati equation (4).
We have the following result on simultaneous local stabilization by the low-and-high-gain feedback.
Theorem 1.
Consider a finite set of linear systems subject to actuator
saturation
\begin{align}
\left[\begin{array}{*{20}c}
\dot{\tilde{x}}_e^i\\
\dot{\tilde{v}}_e^i\\
\end{array}\right]=& \left[\begin{array}{*{20}cc}
A&\;~~0\\
0&\;~~A-BB^{\rm T}P(\varepsilon)\\
\end{array}\right]\left[\begin{array}{*{20}cc}
\tilde{x}_e^i\\
\tilde{v}_e^i\\
\end{array}\right]+\left[\begin{array}{*{20}cc}
B\\
-B\\
\end{array}\right]\times\notag\\
&\ {\rm sat}(\lambda_iu^i),~~i\in\mathcal{N},
\end{align}
(19)
\begin{align}
\lambda_{i_{\min}}(1+\rho)\ge1,
\end{align}
(20)
\begin{align}
u^i=-(1+\rho)B^{\rm T}P(\varepsilon)(\tilde{x}_e^i-
\tilde{v}_e^i),~~i=1,2,\cdots,N,
\end{align}
(21)
Proof. The closed-loop system (19) with the given scheduled low-and-high-gain
feedback law (21) is (18).
We will adopt Lyapunov function
\begin{align}
V^i(\tilde x_e^i,\tilde v_e^i)=\left[\begin{array}{*{20}lll}
{\tilde x_e^i}\\
{\tilde v_e^i}\\
\end{array}\right]^{\rm T}
\left[\begin{array}{*{20}lllllll}
P(\varepsilon)&0\\
0&P(\varepsilon)\\
\end{array}\right]
\left[\begin{array}{*{20}lll}
{\tilde x_e^i}\\
{\tilde v_e^i}\\
\end{array}\right],
\end{align}
(22)
\begin{align}
& \Theta^i(P(\varepsilon))=\Big\{ \left[\begin{array}{*{20}lll}
{\tilde x_e^i}\\
{\tilde v_e^i} \end{array}\right]
\in {\bf R}^{2n}:\left[\begin{array}{*{20}lll}
{\tilde x_e^i}\\
{\tilde v_e^i} \end{array}\right]^{\rm
T}\left[\begin{array}{*{20}lll}
P(\varepsilon)&0\\
0&P(\varepsilon)
\end{array}\right]\times\notag\\
&\qquad \left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i \end{array}\right]\cdot{\rm
tr}\left(\left[\begin{array}{*{20}lll}
B\\
-B
\end{array}\right]^{\rm T}\left[\begin{array}{*{20}lll}
P(\varepsilon)&0\\
0&P(\varepsilon)
\end{array}\right]\times\right.\notag\\
&\qquad\left.
\left[\begin{array}{*{20}lll}
B\\
-B \end{array}\right]\right)\le 1\Big\}.
\end{align}
(23)
From Lemma 2,we have $\Theta^i(P(\varepsilon))\subset{\mathcal{L}}^i(B^{\rm
T}P(\varepsilon))$,where
\begin{align} {\mathcal{L}}^i(B^{\rm
T}P(\varepsilon))=&\ \Big\{\left[\begin{array}{*{20}c}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]\in{\bf R}^{2n}:\left\|\left[\begin{array}{*{20}c}
B\\
-B
\end{array}\right]^{\rm T}\right.{\rm n}n\times\end{align}
(24)
\begin{align}
&\left. \left[\begin{array}{*{20}c}P(\varepsilon)&0\\
0&P(\varepsilon)
\end{array}\right]\left[\begin{array}{*{20}lllll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]\right\|_\infty\le 1\Big\}.
\end{align}
(25)
\begin{align}
{{\rm d}V^i}\over{{\rm d}t}&=\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]^{\rm T} M(\varepsilon)
\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]-2\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]^{\rm T}\left[\begin{array}{*{20}lll}
P(\varepsilon)B\\
-P(\varepsilon)B
\end{array}\right]\times\notag\\
&\ {\rm sat}\Big(\lambda_i(1+\rho)
\left[\begin{array}{*{20}lll}P(\varepsilon)B\\
-P(\varepsilon)B
\end{array}\right]^{\rm T}\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]\Big)=\notag\\
&\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i \end{array}\right]^{\rm
T}\Big(M(\varepsilon)+P(\varepsilon)BB^{\rm
T}P(\varepsilon)\left[\begin{array}{*{20}lll}
-2&2\\
*&-2
\end{array}\right]\Big)\times\notag\\
&\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i\\
\end{array}\right]-2\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i\\
\end{array}\right]^{\rm T}\left[\begin{array}{*{20}lll}
P(\varepsilon)B\\
-P(\varepsilon)B
\end{array}\right]
{\rm sat}\Big(\lambda_i(1+\rho)\times\notag\\
&\left[\begin{array}{*{20}lll}P(\varepsilon)B\\
-P(\varepsilon)B
\end{array}\right]^{\rm T}\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]\Big)+2\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]^{\rm T}\times\notag\\
&\left[\begin{array}{*{20}lll}P(\varepsilon)B\\
-P(\varepsilon)B
\end{array}\right]
\left[\begin{array}{*{20}lll}
B^{\rm T}P(\varepsilon)~&-B^{\rm T}P(\varepsilon)\\
\end{array}\right]
\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]\le\notag\\
&\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]^{\rm T} M(\varepsilon)
\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]-2
\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]^{\rm T}
\left[\begin{array}{*{20}lll}P(\varepsilon)B\\
-P(\varepsilon)B\\
\end{array}\right]\times\notag\\
&\
{\rm sat}\Big(\lambda_i(1+\rho)\left[\begin{array}{*{20}lll}
P(\varepsilon)B\\
-P(\varepsilon)B \end{array}\right]^{\rm
T}\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]\Big)+\notag\\
&\ 2 \left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i\\
\end{array}\right]^{\rm T}
\left[\begin{array}{*{20}lll}P(\varepsilon)B\\
-P(\varepsilon)B
\end{array}\right]
\left[\begin{array}{*{20}lll}
P(\varepsilon)B\\
-P(\varepsilon)B
\end{array}\right]^{\rm T}
\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]=\notag\\
& \left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i
\end{array}\right]^{\rm T} {\left[\begin{array}{c}
{-Q(\varepsilon)+P(\varepsilon)BB^{\rm T}P(\varepsilon) } \\
{*} \end{array}\right.}~~~~~~\nonumber\\
&
\left. \begin{array}{c}
{0 }\\
{-Q(\varepsilon)-P(\varepsilon)BB^{\rm T}P(\varepsilon)}
\end{array}\right] \left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i\\
\end{array}\right]-\notag\\
&\ 2{\displaystyle\sum_{j=1}^m}s_j^i\Big (\;{\rm
sat}(\lambda_i(1+\rho_i)s_j^i)-\;{\rm sat}(s_j^i)\Big),
\end{align}
(26)
From (20) and the fact that
\begin{align*}
s_j^i\;{\rm sat}(s_j^i)>0,~~~\mbox{\rm whenever} ~~s_j^i\neq0,
\end{align*}
we have
\begin{align}
-s_j^i\Big[\;{\rm sat}(\lambda_i(1+\rho_i)s_j^i)-\;{\rm
sat}(s_j^i)\Big]\le0.
\end{align}
(27)
In the sequel,we can obtain the extended result based on Theorem 1.
Corollary 1. Consider a finite set of linear systems subject to actuator saturation defined as in (19). Then,under Assumption 1,the family of low-and-high-gain state feedback laws (21) satisfying (20) semi-globally simultaneously stabilize the $N$ systems in (19). That is,for any given arbitrarily large bounded set $\mathcal{X}\subset{\bf R}^{2n}$,there exists an $\varepsilon^*$ $\in$ $(0,1]$ such that,for any $\varepsilon\in(0,\varepsilon^*],$ the closed-loop system (19) with control (21) is simultaneously asymptotically stable with $\mathcal{X}$ contained in the domain of attraction,where $\lambda_{i_{\rm min}}$ and $\varepsilon$ are the same as in Theorem 1.
Proof. From the proof of Theorem 1,and the fact that $\dot V^i$ $ <$ $0$,we know that $\Theta^i(P(\varepsilon))$ is an invariant subset and contained in the domain of attraction of $i$-th system in (19). Thus,$\Xi(P(\varepsilon),\xi)=\cap\Theta^i(P(\varepsilon))$, $\xi>0$,$i\in\mathcal{N}$ is an invariant subset of domain of attraction of system (19). On the other hand,since the origin is the center of each ellipsoid $\Theta^i(P(\varepsilon))$, $\Xi(P(\varepsilon),\xi)$ is a non-empty set. Moreover,for any given arbitrarily large bounded set $\mathcal{X}\subset{\bf R}^{2n}$,there exists an $\varepsilon^*\in(0,1]$ such that,for any $\varepsilon\in(0,\varepsilon^*]$,$\mathcal{X}\subset\Xi(P(\varepsilon),\xi)$ $\subset$ ${\bf R}^{2n}$ is contained in the domain of attraction. Such an $\varepsilon^*$ exists as $\mathcal{X}$ is bounded,and the $\lim_{\varepsilon\rightarrow{0^+}} P(\varepsilon)=0$.
Based on Theorem 1 and Corollary 1,we can obtain the following theorem.
Theorem 2. Consider the leader-follower multi-agent system (2) and (3). Assume the adjacent graph $\bar{\mathcal{G}}$ composed of $N$ followers and one leader is connected. Then,under Assumption 1,all the followers can track the leader semi-globally via local error low-and-high-gain feedback (9) satisfying $\lambda_{i_{\rm min}}(1+\rho)\ge1$. That is,for any given arbitrarily large bounded set $\mathcal{X}^*\subset{\bf R}^{2n}$, there exists an $\varepsilon^*\in(0,1]$ such that,for any $\varepsilon\in(0,\varepsilon^*],$ all the followers can track the leader asymptotically within $\mathcal{X}^*$ contained in the domain of synchronization,where $\lambda_{i_{\rm min}}$ is the minimum eigenvalue of matrix $H$ corresponding to graph $\bar{\mathcal{G}}$, and $\varepsilon$ is the same as in Corollary 1.
${\bf Proof.}$ Under the orthogonal transformation (15),the
closed-loop system consisting of $N$ agents (2),leader (3) and
the control law (9) can be written as (17). For system (17),
construct the following Lyapunov function candidate
\begin{align}
V(\tilde{x}_e,\tilde v_e)=\left[\begin{array}{*{20}lll}
\tilde x_e\\
\tilde v_e\\
\end{array}\right]^{\rm T}\Big(I_N\otimes \left[\begin{array}{*{20}lll}
P(\varepsilon)&0\\
0&P(\varepsilon)\\
\end{array}\right]\Big)\left[\begin{array}{*{20}lll}
\tilde x_e\\
\tilde v_e\\
\end{array}\right].
\end{align}
(28)
\begin{align}
V(\tilde{x}_e,\tilde v_e)=&\ {\displaystyle\sum_{i=1}^{N}}\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i\\
\end{array}\right]^{\rm T}\left[\begin{array}{*{20}lll}
P(\varepsilon)&0\\
0&P(\varepsilon)\\
\end{array}\right]\left[\begin{array}{*{20}lll}
\tilde x_e^i\\
\tilde v_e^i\\
\end{array}\right]=\notag\\
& \ {\displaystyle\sum_{i=1}^{N}} V^i(\tilde x_e^i,\tilde v_e^i),
\end{align}
(29)
\begin{align}
\dot V(\tilde{x}_e,\tilde{v}_e)
={\displaystyle\sum_{i=1}^{N}}\dot V^i(\tilde{x}_e^i,
\tilde{v}_e^i)
<0,
\end{align}
(30)
Remark 2. The results obtained in this paper are all based on a group of agents with linear systems subject to actuator saturation over a fixed undirected communication topology,and it should be pointed out that based on the result of [24] and Lemma 5 in [25],the method proposed in this paper can also be used to investigate the leader-following consensus problem for such multi-agent systems over the directed graph with a directed spanning tree,as long as the method and its conditions attached to are properly adjusted.
IV. ILLUSTRATIVE EXAMPLE
In this section,an example is given to verify the effectiveness of
the proposed theoretical results in this paper.
${\bf Example 1.}$ Consider a leader-follower multi-agent system (4) with followers satisfying
\begin{align}
\dot x^i=Ax^i+B{\rm sat}(u^i),
\end{align}
(31)
\begin{align}
\dot x_l=Ax_l,
\end{align}
(32)
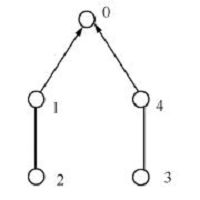
|
Download:
|
| Fig. 1.The adjacent graph $\bar{\mathcal{G}}$. | |
To construct the low-and-high-gain feedback laws (9),we choose $Q(\varepsilon)=\varepsilon I_2$ and solve the algebraic Ricatti equation (4) to obtain the following equation[9] \begin{align*} P(\varepsilon)=\left[\begin{array}{*{20}lll} \tilde{P}_{11}(\varepsilon)~~~~~&~~~~\sqrt{2\varepsilon}-\sqrt{\varepsilon+2\sqrt{2\varepsilon}}\\[2mm] \sqrt{2\varepsilon}-\sqrt{\varepsilon+2\sqrt{2\varepsilon}}~~~~~&~~~~\sqrt{\varepsilon+2\sqrt {2\varepsilon}}\\ \end{array}\right], \end{align*} with $\tilde{P}_{11}(\varepsilon)=\sqrt{\varepsilon+2\sqrt{2\varepsilon}}(1+\sqrt{2\varepsilon} -\sqrt{\varepsilon+2\sqrt{2\varepsilon}})$.
Take $\rho=8$,which satisfies $\lambda_2\rho=3.056>1$, $\varepsilon=0.025$ and the initial values: \begin{align*} &x_e^1(0)=x^1(0)-x_l(0)=[0,-1]^{\rm T},\notag\\ &x_e^2(0)=x^2(0)-x_l(0)=[-4,-3]^{\rm T},\notag\\ &x_e^3(0)=x^3(0)-x_l(0)=[2,-5]^{\rm T},\notag\\ &x_e^4(0)=x^4(0)-x_l(0)=[-3,1]^{\rm T},\notag\\ &v_e^1(0)=[0,-1]^{\rm T},\notag\\ &v_e^2(0)=[-2,-3]^{\rm T},\notag\\ &v_e^3(0)=[-3,-2]^{\rm T},\notag\\ &v_e^4(0)=[-2,1]^{\rm T}. \end{align*}
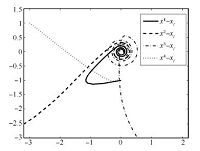
Then,for $x_e^i(0)$, $v_e^i(0)\in{\bf R}^2$,$i\in\mathcal{N}$,we can check that (23) is satisfied. The simulation result of $x^i-x_l$,$i=$ 1,2,3, $4$ is shown in Fig. 2,which indicates that all four followers can track the leader eventually.
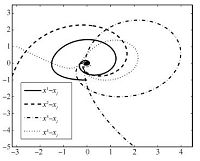
Next,we take $\rho=15$,$\varepsilon$ and the initial values are the same as in Fig. 2. In this case,the simulation of state trajectories of $x^i-x_l$,$i=1,2,3,4$ are shown in Fig. 3. From Figs. 2 and 3,we can conclude that the high-gain parameter $\rho$ can improve the tracking speed indeed.
|
Download:
|
| Fig. 2.Trajectories of $x^i-x_l$. | |
|
Download:
|
| Fig. 3.Trajectories of $x^i-x_l$. | |
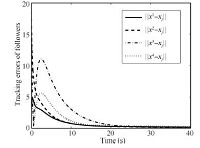
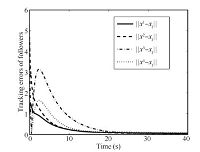
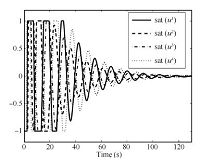
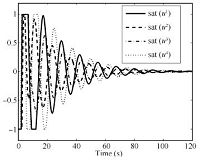
To show that this family of low-and-high-gain feedback laws solve tracking problem semi-globally,we simulate the followers and the leader for different values of the low gain parameter $\varepsilon$. Figs. 4 $\sim$ 7 are the simulation results of states of $\Vert x^i-x_l\Vert$ and controls of ${\rm sat}(u^i)$ under the high-gain parameter $\rho=15$ and the same initial condition as in (32).
|
Download:
|
| Fig. 4.The tracking errors of followers. | |
Figs. 4 and 5 show the $2$-norm of $x^i-x_l$ corresponding to $\varepsilon= 0.025$ and $\varepsilon= 0.001$,respectively,the control of ${\rm sat}(u^i)$ corresponding to $\varepsilon= 0.025$ and $\varepsilon= 0.001$ are presented in Figs. 6 and 7. It is clear from these plots that for the given initial state,the peak value of the control ${\rm sat}(u^i)$ decreases as the value of the low-gain parameter decreases,which indicates that the tracking problem can be solved semi-globally.
|
Download:
|
| Fig. 5.The tracking errors of followers. | |
|
Download:
|
| Fig. 6.rajectories of ${\rm sat}(u^i)$. | |
|
Download:
|
| Fig. 7.Trajectories of ${\rm sat}(u^i)$. | |
In this paper,we have investigated the tracking problem of leader-follower multi-agent systems subject to actuator saturation. An active leader node or control node generates the desired tracking trajectories. To track such a leader,we have proposed a new family of scheduled low-and-high-gain feedback controller laws which rely on the asymptotical property of a class of parametric algebraic Ricatti equations. Our control law is equipped with a design parameter that can be adjusted to track the leader semi-globally for all the followers. An illustrative example with simulations shows the effectiveness of the method proposed for the multi-agent systems with actuator saturation and an active leader. Future research will be concentrated on applying the results to investigate the tracking problem of leader-follower for multi-agent systems over the directed graph with a directed spanning tree,or over a switched communication topology.
| [1] | Hu T S, Lin Z L. Control Systems with Actuator Saturation:Analysis and Design. Boston:Birkhäuser, 2001 |
| [2] | Lin Z L, Saberi A. Semi-global exponential stabilization of linear systems subject to "input saturation" via linear feedbacks. Systems and Control Letters, 1993, 21(3):225-239 |
| [3] | Chen B M, Lee T H, Peng K M, Venkataramanan V. Composite nonlinear feedback control for linear systems with input saturation:theory and an application. IEEE Transactions on Automatic Control, 2003, 48(3):427-439 |
| [4] | da Silva J M G, Tarbouriech S. Local stabilization of discrete-time linear systems with saturating controls:an LMI-based approach. IEEE Transactions on Automatic Control, 2001, 46(1):119-125 |
| [5] | Wei A R, Wang Y Z. Stabilization and H∞ control of nonlinear portcontrolled hamiltonian systems subject to actuator saturation. Automatica, 2010, 46(12):2008-2013 |
| [6] | Cao Y Y, Lin Z L, Ward D G. Anti-windup design of output tracking systems subject to actuator saturation and constant disturbances. Automatica, 2004, 40(7):1221-1228 |
| [7] | Zhou B, Duan G G, Lin Z L. A parametric Lyapunov equation approach to the design of low gain feedback. IEEE Transactions on Automatic Control, 2008, 53(6):1548-1554 |
| [8] | Sabrei A, Hou P, Stoorvogel A A. On simultaneous global external and global internal stabilization of critically unstable linear systems with saturating actuators. IEEE Transactions on Automatic Control, 2000, 45(6):1042-1052 |
| [9] | Lin Z L. Low Gain Feedback. London:Springer-Verlag, 1998. |
| [10] | Teel A R. Semi-global stabilizability of linear null controllable systems with input nonlinearities. IEEE Transactions on Automatic Control, 1995, 40(1):96-100 |
| [11] | Lin Z L. H∞-almost disturbance decoupling with internal stability for linear systems subject to input saturation. IEEE Transactions on Automatic Control, 1997, 42(7):992-995 |
| [12] | Olfati-Saber R, Fax J A, Murray R M. Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE, 2007, 95(1):215-233 |
| [13] | Ren W, Beard R, Atkins E. A survey of consensus problems in multiagent coordination. In:Proceedings of the 2005 American Control Conference. Portland, OR, USA:IEEE, 2005. 1859-1864 |
| [14] | Fax J A, Murray R M. Information flow and cooperative control of vehicle formations. IEEE Transactions on Automatic Control, 2004, 49(9):1465-1476 |
| [15] | Hong Y G, Hu J P, Gao L X. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica, 2006, 42(7):1177-1182 |
| [16] | Li X, Wang X F, Chen G R. Pinning a complex dynamical network to its equilibrium. IEEE Transactions on Circuits and Systems-I:Regular Papers, 2004, 51(10):2074-2087 |
| [17] | Ren W, Moore K L, Chen Y Q. High-order and model reference consensus algorithms in cooperative control of multi-vehicle systems. Journal of Dynamic Systems, Measurement, and Control, 2007, 129(5):678-688 |
| [18] | Jadbabaie A, Lin J, Morse A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Transactions on Automatic Control, 2003, 48(6):988-1001 |
| [19] | Gustavi T, Dimarogonas D, Egerstedt M, Hu X M. Sufficient conditions for connectivity maintenance and rendezvous in leader-follower networks. Automatica, 2010, 46(1):133-139 |
| [20] | Hong Y G, Chen G R, Bushnell L. Distributed observers design for leader-following control of multi-agent networks. Automatica, 2008, 44(3):846-850 |
| [21] | Nedic A, Ozdaglar A, Parrilo P A. Constrained consensus and optimization in multi-agent networks. IEEE Transactions on Automatic Control, 2010, 55(4):922-938 |
| [22] | Cortés J. Finite-time convergent gradient flows with applications to network consensus. Automatica, 2006, 42(11):1993-2000 |
| [23] | Yang T, Stoorvogel A A, Grip H F, Saberi A. Semi-global regulation of output synchronization for heterogeneous networks of non-introspective, invertible agents subject to actuator saturation. International Journal of Robust and Nonlinear Control, doi:10.1002/rnc.2905 |
| [24] | Meng Z Y, Zhao Z Y, Lin Z L. On global leader-following consensus of identical linear dynamic systems subject to actuator saturation. Systems and Control Letters, 2013, 62(2):132-142 |
| [25] | Li Z K, Duan Z S, Chen G R, Huang L. Consensus of multiagent systems and synchronization of complex networks:a unified viewpoint. IEEE Transactions on Circuits and Systems-I:Regular Papers, 2010, 57(1):213-224 |
 2014, Vol.1
2014, Vol.1 


