2. Department of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu 610054, China;
3. Department of Electrical and Computer Engineering, National University of Singapore, Singapore 117576, Singapore
Research on multi-agent systems (or networked cooperative systems) with applications to the cooperation of unmanned aerial vehicles (UAVs),autonomous underwater vehicles (AUVs),robots,scheduling of automated highway systems has attracted much attention in the past two decades[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]. Efforts towards stabilization and tracking control of multi-fully actuated ocean surface vessels as the need for rescuing,exploring and preserving the oceanic environments have gained significant momentum.
In most of the present work,every agent is required to follow a specified path or track a predefined position in the formation[9, 10, 11, 12]. Nonlinear robust adaptive control strategy was developed to force an underactuated surface ship to follow a predefined path at a desired speed in [13]. Moreover,feedback control law was designed to stabilize the underactuated vessel to a desired constant position and orientation in [14]. In [15],a combination of line-of-sight path following and nonlinear synchronization strategies was studied. Nontrivial coordinate changes,graph theory,and stability theory of linear time-varying systems were used to design cooperative control laws for underactuated vessels to perform a geometric pattern[2].
It is interesting to observe from examples of group behavior in the nature that accurate specification of the path of each agent in the group seems to be not necessary. Swarming behavior is more common where agents are loosely distributed within a moving target region,not requiring specific orders or positions of the agents inside the region. The region reaching control concept was presented for robot manipulator,in which the desired objective can be specified as a region instead of a point in [16],and [17] proposed the new region-reaching controller for an underwater vehicle mounted with a manipulator. It has been shown that region reaching tasks save energy and result in faster motion. In [18],an adaptive region boundary-based concept was presented for an AUV,in which the controller was designed to allow the convergence of the vehicle to the boundary or a motionless region surface regardless of its initial position. Region following formation control concept has been proposed[19, 20],where all the robots stay within a moving region as a group,while maintaining a minimum distance among themselves. Recently,the region following control concept has been developed for general multi-agent systems with high-order dynamics in previous work[21].
In this paper,we propose a decentralized cooperative controller for multi-fully actuated ocean vessel systems. A group of ocean vessels with limited sensing ranges are driven into a moving target region without collisions,and the connectivity preservation of the dynamic interaction network is guaranteed. By using the objective function,the desired region can be specified as an arbitrary shape,and hence we can form different formations. The decentralized controller permits the ocean vessels in the group to only communicate with their neighbors. It reduces communication or sensing requirement,and is relatively more scalable with respect to the group size. We introduce the artificial potential functions to preserve the connectivity of the network and guarantee no collisions between any ocean vessels[22, 23]. The chosen potential functions possess the special property of approaching infinity whenever its arguments approach some limits[24, 25].
The handling of unknown perturbations to the nominal model,in the form of parametric and functional uncertainties,unmodeled dynamics,and disturbances from the environment,is an important issue of model-based control of ocean vessels. Traditional model-based adaptive controllers may not be applicable since they are useful only when dealing with systems in which the dynamics are linear-in-the-parameters,the uncertainties are parametric and time-invariant,and the regressors are exactly known[26]. For overcoming the limitations of model-based adaptive controllers,we adopt approximation-based control techniques to compensate for functional uncertainties and unknown disturbances from the environment.
The main contributions of this work are listed as follows:
1) The detailed theoretical formation,which can enable a swarm of multi-fully actuated ocean surface vessels to track a moving target region,is proposed in the presence of uncertainties and unknown disturbances.
2) The artificial potential function is subtly introduced to preserve the connectivity of the network. Connectivity is a common assumption in the consensus analysis of multi-agent systems. In fact,it is not always valid in the networked systems whose sensors are distance dependent,and thus in order to accomplish a cooperative task,the connectivity of the network is required to be maintained.
3) The collision avoidance potential function is chosen to prevent the collisions between vessels when they are inside their danger ranges. Especially,the length of vessel is considered in the designing such that the collision avoidance function approaches infinity whenever any other vessels come in contact with the vessel,i.e.,a collision occurs.
4) The approximation-based controller for fully actuated surface vessels is designed using Lyapunov synthesis. Such approximators can use a standard regressor function whose structure is independent of the ocean vessel's dynamic characteristics,thus it increases the portability of the same control algorithm on different ocean vessel systems.
The remainder of the paper is organized as follows. In Section II,the problem is stated and some preliminaries are presented. In Section III,the region tracking controller of multi-fully actuated surface vessel systems is designed and the effectiveness of our algorithm is analysed. In Section IV,simulation results are presented to illustrate the performance of the proposed region tracking controller. Finally,we conclude the paper in Section V.
II. PROBLEM FORMULATION
A.Vessel Dynamics
Consider a group of $N$ fully actuated vessels,and the
multiple-input-multiple-output (MIMO) dynamics of the 3
degrees-of-freedom (3DOF) vessel $i$ is
\begin{align}
&\dot\eta_i=R_i(\eta_i)\nu_i,{\rm n} num\end{align}
(1)
\begin{align}
&M_i\dot\nu_i=\tau_i-C_i(\nu_i)\nu_i-D_i(\nu_i)\nu_i+R_i(\eta_i)^{\rm
T}d_i,
\end{align}
(2)
\begin{align}
&\dot\eta_i=R_i(\eta_i)\nu_i,\label{remodel}{\rm n}num \end{align}
(3)
\begin{align}
&M_i\dot
\nu_i=\tau_i-C_i(\nu_i)\nu_i+\kappa_i(\nu_i)+g_i(\eta_i,\nu_i),
\end{align}
(4)
|
Download:
|
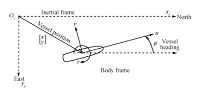
| Fig. 1.Figure showing the inertial earth-fixed frame and the body-fixed frame for a vessel. | |
${\bf Assumption 1.}$ All vessels have the same characteristics.
We associate the vessels with nodes in a graph and information exchange with its edges. The communication graph $\mathcal{G}$ is defined for describing the inter-vessel communication. We use ${G}_i$ to denote the set of indices for those vessels having communication with vessel $i$.
${\bf Assumption 2.}$ The communication graph $\mathcal{G}$ is an undirected graph and connected initially.
${\bf Definition 1.}$ The undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ consists of a set of vertices $\mathcal{V}=\{1,\cdots,N\}$ indexed by the group members,and a set of edges,$\mathcal{E}=\{(i,j)\in \mathcal{V}\times\mathcal{V}\big|i\in {G}_j\}$ containing pairs of nodes that show inter-vessel communication specifications.
${\bf Assumption 3.}$ Each vessel has a communication range $R$.
For simplicity,we assume that all vessels move in a
two-dimensional (2-D) workspace. Their position in the workspace is
denoted by $q_i=[x_i,y_i]^{\rm T}$,and $\eta_i=[q_i^{\rm
T},\psi_i]^{\rm T}$. The set ${G}_i$ can be defined as the set that
vessel $i$ can communicate when it is located at its initial
position:
\begin{align}
{G}_i=\left\{j\in\mathcal{V},j\neq i~\big|\| q_i(0)-q_j(0)\| \leq
R\right\}.
\end{align}
(5)
|
Download:
|
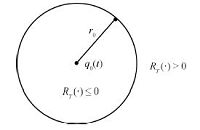
| Fig. 2.Illustration of the target region function. | |
${\bf Assumption 4.}$ The position $q_0(t)$ and velocity $\dot q_0(t)$ of the center of the moving target region are continuous and bounded.
${\bf Assumption 5.}$ The target region is big enough to accommodate all vessels and their own communication ranges.
In the later part of this paper,the time argument will be omitted
if no confusion is expected. We mathematically formulate the control
objective by defining the variable $\psi_{i,d}$ as $\arctan ({\dot
q_{0,y}\over \dot q_{0,x}})$. Then,the function for the control
objective is presented as
\begin{align}
F_i(\tilde \eta_{id})=&\ (x_i-q_{0,x})^2+(y_i-q_{0,y})^2 -r_0^2+(\psi_{i}-\psi_{i,d})^2={\rm n}num\end{align}
(6)
\begin{align}
&\ \|\tilde \eta_{id}\|^2-r_0^{2},
\end{align}
(7)
B.Potential Functions
The potential functions consist of target tracking function, collision avoidance function,and connectivity maintenance function,which are specified as below.
1) Target tracking function:
The target tracking function is designed for each vessel to track
the common target region by putting a penalty on the tracking
errors. The target tracking function ${P_{i,0}}:{{\bf{R}}^3} \to {\bf{R}}$
for vessel $i$ is chosen as follows:
\begin{align}
P_{i,0}(\tilde\eta_{id} )&=&\begin{cases}
0,&R_{T_i}( \tilde q_{i,0})\leq0,\\[2mm]
{\dfrac{c_i}{ 2}}F_i^2( \tilde\eta_{id}),& R_{T_i}( \tilde
q_{i,0})>0,
\end{cases}
\end{align}
(8)
1) $P_{i,0}=0$,if $R_{T_i}(\tilde q_{i,0})\leq0$;
2) $P_{i,0}>0$,if $R_{T_i}(\tilde q_{i,0})>0$;
3) $P_{i,0}\to\infty $,if $R_{T_i}(\tilde q_{i,0})\to\infty.$
2) Collision avoidance function:${\bf Definition 2.}$ Each vessel has a danger range,which is centered at the vessel,with radius $r$ $(r<R)$.
To prevent the collisions between vessels when they are inside
their danger ranges,the collision avoidance function is chosen.
${H}_i$ is presented to denote the set containing all those
vessels within the danger range of vessel $i$ as follows ${H}_i
=\left\{ j\in \mathcal{V},j\neq i\ \big|\| \tilde
q_{i,j}\|^2-r^2\leq 0\right\},$ where $\tilde
q_{i,j}=q_{i}-q_{j}$. The collision avoidance function $P_{i,j}$
for vessel $i$ is chosen as follows:
\begin{align}
\label{collpot} P_{i,j}(\tilde
q_{i,j})=\begin{cases}
0,& \| \tilde q_{i,j}\|>r,\\
c_{i,j}\ln \left(\dfrac{r^2-L^2}{\| \tilde
q_{i,j}\|^2-L^2}\right)^2,& \| \tilde q_{i,j}\| \leq r,
\end{cases}
\end{align}
(9)
1) $P_{i,j}=0$,if $\|\tilde q_{i,j} \|>r$;
2) $P_{i,j}>0$,if $\|\tilde q_{i,j} \|\leq r$;
3) $P_{i,j}$ is monotonically increasing with the decreasing of $\|\tilde q_{i,j} \|$,if $\|\tilde q_{i,j} \|\leq r$;
4) $P_{i,j}\to\infty$,if $\|\tilde q_{i,j} \|\to L$.
3) Connectivity maintenance function:
Connectivity is a common assumption in the consensus analysis of
multi-agent systems. In fact,it is not always valid in the
networked systems whose sensors are distance dependent. Therefore
the connectivity maintenance potential function is designed to
preserve the connectivity of the network,that is,the vessels are
initially located in the communication zone of a vessel,and they
will remain in this area for all time. We define the connectivity
maintenance function as follows:
\begin{align}
Q_{i,j}( \tilde
q_{i,j})=c'_{i,j}\ln \left( \dfrac{R^2}{R^2-\| {\tilde
q}_{i,j}\|^2}\right)^2,
\end{align}
(10)
1) $Q_{i,j}\to\infty$,if $\|\tilde q_{i,j} \|\to { R}$;
2) $Q_{i,j}$ is continuous and differentiable,$\forall \|\tilde q_{i,j} \|$ $\in$ $[0,{ R})$.
C. Function Approximation
In control engineering,linearly parameterized neural network has been successfully used to approximate the following unknown continuous function $F_i(Z_i):{\bf R}^q \to \bf{R}$ for $i$-th vessel[27, 28]: $F_i(Z_i)=\phi_i^{\rm T}(Z_i)\varphi_i+\varepsilon_i(Z_i),$ where $Z_i=[z_{i1},z_{i2},\cdots,z_{iq}]^{\rm T}\in {\bf R}^q$ is the input vector,$\varphi_i$ $\in$ ${\bf R}^{l}$ is the weight vector with the neural network node number $l$,$\phi_i(Z_i)\in {\bf R}^{l}$ is a vector of known continuous basis functions,and $\varepsilon_i(Z_i)$ is called the neural network approximation error which satisfies $|\varepsilon_i(Z_i)|\leq \varepsilon_i^{*}$,$\forall Z_i\in \Omega_{Z_i}$ with the unknown constant $\varepsilon_i^{*}>0$.
According to the universal approximation property,if $l$ is chosen sufficiently large,$\phi_i^{\rm T}(Z_i)\varphi_i$ can smoothly approximate any continuous function $F_i(Z_i)$ over a compact set $\Omega_{Z_i}$ $\subset$ ${\bf R}^q$ to an arbitrary degree of accuracy as $F_i(Z_i)=\phi_i^{\rm T}(Z_i)\varphi_i^*+\varepsilon_i(Z_i),\quad \forall Z_i\in \Omega_{Z_i}\subset {\bf R}^q,$ where $\varphi_i^*$ is the ideal constant weight vector,and $\varepsilon_i(Z_i)$ is the approximation error for the special case where $\varphi_i=\varphi_i^*$. The ideal weight vector $\varphi_i^*$ is an artificial quantity required for analytical purposes. $\varphi_i^*$ is defined as the value of $\varphi_i$ that minimizes $|\varepsilon_i|$ for all $Z_i\in \Omega_{Z_i}\subset {\bf R}^q$,that is $ \varphi_i^*=\arg\min_{\varphi_i\in{\bf R}^l}\Big\{ \sup _{Z_i\in\Omega_{Z_i}}|F_i(Z_i)-\phi_i^{\rm T}(Z_i)\varphi_i|\Big\}. $
${\bf Lemma 1}$[29]. The following inequality holds for any $\epsilon$ $>$ $0$ and for any $\eta\in \bf{R}$ $ 0\leq|\eta|-\eta\tanh\bigg( {\eta\over \epsilon}\bigg)\leq \kappa\epsilon,{\rm n}num $ where $\kappa$ is a constant that satisfies $\kappa=\exp[-(\kappa+1)]$,i.e.,$\kappa$ $=$ $0.2785$. The scalar $\epsilon>0$ is a (small) positive design constant,and $\tanh(\cdot)$ denotes the hyperbolic tangent function.
III. CONTROL DESIGN AND STABILITY ANALYSIS
In this section,we present the decentralized adaptive neural
network control scheme for vessel $i$ to achieve the control
objective. Feedforward approximators are used to compensate for
unknown nonlinear functions. Using the potential functions in the
first step of recursion,we can guarantee that all vessels can
track the moving target region without collisions,and the
connectivity of the network remains for all time. The second step
follows the standard backstepping procedure with the quadratic
Lyapunov functions[30]. According to the analysis above,the
whole potential function can be written as $
V_{1}=\sum_{i=1}^{N}P_{i,0} +\sum_{i=1}^{N}\sum_{j\in { H}
_{i}}P_{i,j} +\sum_{i=1}^{N}\sum_{j\in { G}_{i}}Q_{i,j}. $ Then,
the derivative of $V_1$ can be expressed as
\begin{align}
\dot{V}_{1}=&\ \sum_{i=1}^{N}\big(\frac{\partial
P_{i,0}}{\partial\tilde{\eta}_{id}}\dot{\tilde{\eta}}_{id}+
\sum_{j\in { H}_{i}}\frac{\partial P_{i,j}}{\partial{\tilde
q}_{i,j}}\dot{\tilde{q}}_{i,j}+ \sum_{j\in { G}_{i}}\frac{\partial
Q_{i,j}}{\partial{\tilde
q}_{i,j}}\dot{\tilde{q}}_{i,j}\big)={\rm n}num \end{align}
(11)
\begin{align}
&\ \sum_{i=1}^{N}\frac{\partial
P_{i,0}}{\partial\tilde{\eta}_{id}}(\dot{\eta}_{i}
-\dot{\eta}_{i,d})+\sum_{i=1}^{N}
\sum_{j\in { H}_{i}}\frac{\partial P_{i,j}}{\partial{\tilde q}_{i,j}}(\dot{q}_{i}-\dot{q}_{j}) +{\rm n}num \end{align}
(12)
\begin{align}
&\ \sum_{i=1}^{N}\sum_{j\in { G}_{i}}\frac{\partial
Q_{i,j}}{\partial{\tilde q}_{i,j}}(\dot{q}_{i}-\dot{q}_{j}).
\end{align}
(13)
\begin{align}
&\sum_{i=1}^{N}\sum_{j\in { H}_{i}}\dfrac{\partial
P_{i,j}}{\partial{\tilde q}_{i,j}}(\dot{q}_{i}-\dot{q}_{j})={\rm n}num \end{align}
(14)
\begin{align}
&\qquad \sum_{i=1}^{N}\sum_{j\in { H}_{i}}\dfrac{\partial
P_{i,j}}{\partial{\tilde
q}_{i,j}}[(\dot{q}_{i}-\dot{q}_{0})-(\dot{q}_{j}-\dot{q}_{0})]={\rm
n}num\end{align}
(15)
\begin{align} &\qquad \sum_{i=1}^{N}\sum_{j\in {
H}_{i}}\left[\dfrac{\partial P_{i,j}}{\partial{
q}_{i}}(\dot{q}_{i}-\dot{q}_{0})-\dfrac{\partial
P_{i,j}}{\partial{ q}_{i}}
(\dot{q}_{j}-\dot{q}_{0})\right]={\rm n}num\end{align}
(16)
\begin{align}
&\qquad 2\sum_{i=1}^{N}\sum_{j\in { H}_{i}}\dfrac{\partial
P_{i,j}}{\partial{ q}_{i}}(\dot{q}_{i}-\dot{q}_{0}).
\end{align}
(17)
\begin{align}
\dot{V}_{1}
=&\ \sum_{i=1}^{N}\frac{\partial P_{i,0}}{\partial\tilde{\eta}_{id}}(\dot{\eta}_{i} -
\dot{\eta}_{i,d})+2\sum_{i=1}^{N}\sum_{j\in {H}_{i}}
\frac{\partial P_{i,j}}{\partial{q}_{i}}(\dot{q}_{i}-\dot{q}_{0}) +{\rm n}num\end{align}
(18)
\begin{align}
&\ 2\sum_{i=1}^{N}\sum_{j\in {G}_{i}}\frac{\partial Q_{i,j}}{\partial{q}_{i}}(\dot{q}_{i}-\dot{q}_{0}).
\end{align}
(19)
\begin{eqnarray}
\dot{V}_{1} = \sum_{i=1}^{N}\nabla_{\eta_{i}}
V_{1}\cdot(\dot{\eta}_{i} -\dot{\eta}_{i,d}),\label{eq:nabla1}
\end{eqnarray}
(20)
${\bf Step 1.}$ Denote the error coordinates
\begin{align}
&z_{i,1} = \eta_{i}-\eta_{i,d}\label{z1},\end{align}
(21)
\begin{align}
&z_{i,2} = \nu_{i}-\alpha_{i},\end{align}
(22)
\begin{align}
&\tilde{\varphi}_{i} = \varphi_{i}^{*}-\hat{\varphi}_{i},
\end{align}
(23)
\begin{eqnarray}
\dot{z}_{i,1} =
R_{i}(\eta_{i})\nu_{i}-\dot{\eta}_{i,d}.\label{dotz1}
\end{eqnarray}
(24)
\begin{eqnarray}
\dot{V}_{1} =
\sum_{i=1}^{N}\nabla_{\eta_{i}}V_{1}\cdot[R_{i}(\eta_{i}) \nu_{i}-
\dot{\eta}_{i,d}].
\end{eqnarray}
(25)
\begin{align}
\dot{V}_{1}=& -\sum_{i=1}^{N}k_{i,1}\|\nabla_{\eta_{i}}V_{1}\|^{2} +\sum_{i=1}^{N}
\nabla_{\eta_{i}}V_{1}\cdot R_{i}(\eta_{i})z_{i,2}\leq{\rm n}num\end{align}
(26)
\begin{align}
& -\sum_{i=1}^{N}k_{i,1}^{'}\| \nabla_{\eta_{i}}V_{1}\|^{2}
+\varepsilon,\end{align}
(27)
${\bf Step 2.}$ In this step,we design the control law recursively
to stabilize the error dynamics of $z_{i,2}$. Differentiating
$z_{i,2}$ with respect to time yields
\begin{equation}
\dot{z}_{i,2} =M_{i}^{-1}
\big[\tau_{i}-C_{i}(\nu_{i})\nu_{i}+\kappa_{i}(\nu_{i})
+\phi_{i}^{\rm T}\varphi_{i}^{*}+\varepsilon_{i}\big]
-\dot{\alpha}_{i}.
\end{equation}
(28)
\begin{equation}
V_{2}=V_{1}+\sum_{i=1}^{N}\frac{1}{2} z_{i,2}^{\rm T} z_{i,2}+
\sum_{i=1}^{N} \frac{1}{2} \tilde{\varphi}_{i}^{\rm
T}\Gamma_{i}^{-1}\tilde{\varphi}_{i},
\end{equation}
(29)
\begin{align}\label{dv2}
\dot{V}_{2}
= & -\sum_{i=1}^{N} k_{i,1}\|\nabla_{\eta_{i}}V_{1} \|^{2} +\sum_{i=1}^{N}\nabla_{\eta_{i}}V_{1}
\cdot R_{i}(\eta_{i})z_{i,2} +{\rm n}num\end{align}
(30)
\begin{align}
& \ \sum_{i=1}^{N}z_{i,2}^{\rm T}\{M_{i}^{-1} \big[\tau_{i}-C_{i}(\nu_{i})\nu_{i} +
\kappa_{i}(\nu_{i}) +{\rm n}num
\end{align}
(31)
\begin{align}
& \ \phi_{i}^{\rm T}\varphi_{i}^{*}+ \varepsilon_{i}\big]-\dot{\alpha}_{i}\}
-\sum_{i=1}^{N}\tilde{\varphi}_{i}^{\rm T}
\Gamma_{i}^{-1}\dot{\hat{\varphi}}_{i}.
\end{align}
(32)
\begin{align}
\tau_{i} = & -M_{i}R_{i}^{\rm T}(\eta_{i})\nabla_{\eta_{i}}^{\rm T} V_{1}-
k_{i,2}M_{i}z_{i,2} +C_{i}(\nu_{i})\nu_{i} -{\rm n}num\label{control}
\end{align}
(33)
\begin{align}
& \ \kappa_{i}(\nu_{i})-\phi_{i}^{\rm T}\hat{\varphi}_{i}+M_{i}\dot{\alpha}_{i}
-\varepsilon_{i}^{*}\tanh \big(\frac{z_{i,2}^{\rm T} M_{i}^{-1}\varepsilon_{i}^{*}}{\epsilon_{i}}\big),
\end{align}
(34)
\begin{align}
\dot{\hat{\varphi}}_{i} = &\ \Gamma_{i}(\phi_{i}M_{i}^{-1}z_{i,2}-
\sigma_i \hat{\varphi}_i). \label{update} \end{align}
(35)
\begin{align}
\dot{V}_{2} = & -\sum_{i=1}^{N}k_{i,1}\|\nabla_{\eta_{i}}V_{1}\|^{2} -\sum_{i=1}^{N}k_{i,2}\|z_{i,2}\|^{2}
+ \label{stabilization}{\rm n}num
\end{align}
(36)
\begin{align}
&\ \sum_{i=1}^{N}\bigg[z_{i,2}^{\rm T}M_{i}^{-1}\varepsilon_{i} -z_{i,2}^{\rm T}
M_{i}^{-1}\varepsilon_{i}^{*} \tanh\big(\frac{z_{i,2}^{\rm
T}M_{i}^{-1}
\varepsilon_{i}^{*}} {\epsilon_{i}}\big)\bigg] +{\rm n}num
\end{align}
(37)
\begin{align}
&\ \sum_{i=1}^N\tilde\phi_i^{\rm T}\sigma_i(\varphi_i^{*}-
\tilde\varphi_i),
\end{align}
(38)
\begin{align}&&z_{i,2}^{\rm
T}M_{i}^{-1}\varepsilon_{i} -z_{i,2}^{\rm
T}M_{i}^{-1}\varepsilon_{i}^{*} \tanh\big(\frac{z_{i,2}^{\rm
T}M_{i}^{-1} \varepsilon_{i}^{*}}
{\epsilon_{i}}\big)\leq\kappa\epsilon_i,{\rm n}num
\end{align}
(39)
\begin{align}
\dot{V}_{2} \leq & -\sum_{i=1}^{N}k_{i,1}\|\nabla_{\eta_{i}}V_{1}\|^{2} -
\sum_{i=1}^{N}k_{i,2}\|z_{i,2}\|{}^{2} - {\rm n}num
\end{align}
(40)
\begin{align}
&\ \sum_{i=1}^N{\sigma_i\parallel \tilde \varphi_i\parallel^2\over
2}+c_0,
\end{align}
(41)
${\bf Theorem 1.}$ Consider the vessel dynamics (1) under Assumptions 1 $\sim$ 5,with region tracking control law (34) and the update law (35). For initial conditions starting in any compact set $\Omega_0$,the whole potential function $V_1$ can converge to a bounded compact set,which gives rise to the convergence of $\eta_i$,$i=1,2,\cdots,N$,to the desired target set,with the connectivity of the network maintained,while no collisions happen between any vessels for all $t>0$.
${\bf Proof.}$ First,we prove the convergence of vessel $i$ to the common moving target region.
Since the whole artificial potential function $V_1$ is bounded,the potential functions $P_{i,0}$,$P_{i,j}$,and $Q_{i,j}$ are all bounded. Therefore,the tracking error of each ocean vessel can converge to an adjustable neighborhood of the origin,although some of them do not access the desired target region directly.
Next,we show that there are no collisions between any vessels, and the connectivity of the network can be maintained for all time.
Since the function $P_{i,j}$ is bounded,hence,according to the property of $P_{i,j} $,$\parallel \tilde q_{i,j}\parallel> L$, i.e.,there are no collisions between any vessels for all $t>0$. Similarly,according to the property of $Q_{i,j} $,we can obtain $\parallel\tilde q_{i,j}\parallel < R$,that is,the connectivity of the network can be maintained for all $t$ $>$ $0$.
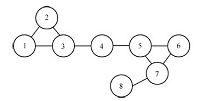
IV. SIMULATION RESULTSIn our simulation study,we consider the model vessel called CyberShip II,a 1 : 70 scale supply vessel replica built in a marine control laboratory in the Norwegian University of Science and Technology. The model can be rewritten as (2),with parameters obtained from [26]. Fig. 3 shows the communication relationships among vessels.
|
Download:
|
| Fig. 3.Communication topology. | |
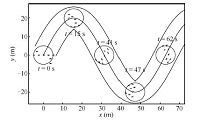
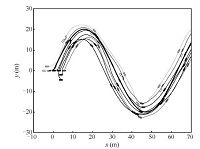
We consider a group of vessels with $N=8$,the danger range radius $r=2.0$ m and the communication range radius $R=3.0$ m. The vessels are initialized randomly around the target region with $q_0(0)=[0.0$,$0.0]^{\rm T}$,$\eta_1(0)=[-5.0$,$0.0$,$0.0]^{\rm T}$,$\eta_2(0)=[-3.5$,$2.0$,$0.0]^{\rm T}$,$\eta_3(0)=[-2.5$, 0.0,$0.0]^{\rm T}$,$\eta_4(0)=[0.0$,0.0,$0.0]^{\rm T}$, $\eta_5(0)= [2.5$,0.0,$0.0]^{\rm T}$,$\eta_6(0)=[5.0$,0.0, $0.0]^{\rm T}$,$\eta_7(0)=[3.5$,$-2.0$,$0.0]^{\rm T}$, $\eta_8(0)=[3.5$,$-4.5$,$0.0]^{\rm T}$. The center of the common target region,$q_0$,moves along the desired trajectory $q_0(t)=[t$,$20\sin(0.1t)]^{\rm T}$ with $r_0$ $=$ $5.0$ m. Simulation results are shown in Figs. 4 $\sim$ 6.
|
Download:
|
| Fig. 4.A group of vessels synchronously tracking the target region. | |
|
Download:
|
| Fig. 5.Trajectories of the ocean vessels. | |
|
Download:
|
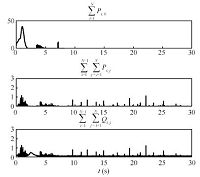
| Fig. 6.Potential functions. | |
Fig. 4 clearly shows the tracking process of all vessels which can successfully track the common moving target region,and the boundness of $P_{i,0}$ in Fig. 6 further confirms it. The trajectories of all vessels and the center of the moving target region are shown in Fig. 5. We can see all vessels can synchronously track the center of the moving target region. From Figs. 4 and 5,we can also find the connectivity of the network remains for all time. Moreover,the boundness of the connectivity maintenance function,$Q_{i,j}$,in Fig. 6 further confirms the connectivity maintenance. Fig. 6 also shows the boundness of collision avoidance function $P_{i,j}$. Therefore,we obtain that no collisions among vessels can be guaranteed.
V. CONCLUSIONIn this paper,due to the advantages of the target region tracking control for achieving better performance and energy saving,stable approximation-based region tracking control has been designed for a group of surface vessels in the presence of time-varying environmental disturbances,unmodeled dynamics,or parametric/functional uncertainties. Simulation results have demonstrated that all vessels can successfully track the common moving target region without collisions. At the same time,the connectivity of the network can be maintained for all time.
AcknowledgementsThe authors would like to thank Dr. Ren Bei-Bei,who is affiliated with Department of Mechanical Engineering,Texas Tech University, USA,for her valuable inputs to the paper.
| [1] | Ren W. Consensus strategies for cooperative control of vehicle formations. IET Control Theory and Applications, 2007, 1(2):505-512 |
| [2] | Dong W, Farrell J A. Formation control of multiple underactuated surface vessels. IET Control Theory and Applications, 2008, 2(12):1077-1085 |
| [3] | Fua C H, Ge S S, Lim K W. Agent formations in 3D spaces with communication limitations using an adaptive Q-structure. Robotics and Autonomous Systems, 2010, 58(4):333-348 |
| [4] | Fax J A, Murray R M. Information flow and cooperative control of vehicle formations. IEEE Transactions on Automatic Control, 2004, 49(9):1465-1476 |
| [5] | Fua C H, Ge S S, Do K D, Lim K W. Multirobot formations based on the queue-formation scheme with limited communication. IEEE Transactions on Robotics, 2007, 23(6):1160-1169 |
| [6] | Açikmeşe B, Hadaegh F, Scharf D, Ploen S. Formulation and analysis of stability for spacecraft formations. IET Control Theory and Applications, 2007, 1(2):461-474 |
| [7] | Cui R X, Ge S S, How V E B, Choo Y S. Leader-follower formation control of underactuated AUVs with leader position measurement. Ocean Engineering, 2010, 37(17-18):1491-1502 |
| [8] | Guo J, Yan G, Lin Z, Cao M. Adaptive control schemes for mobile robot formations with triangularised structures. IET Control Theory and Applications, 2010, 4(9):1817-1827 |
| [9] | Egerstedt M, Hu X M. Formation constrained multi-agent control. IEEE Transactions on Robotics and Automation, 2001, 17(6):947-951 |
| [10] | Ghommam J, Mehrjerdi H, Saad M, Mnif F. Formation path following control of unicycle-type mobile robots. Robotics and Autonomous Systems, 2010, 58(5):727-736 |
| [11] | Park B S, Yoo S J, Park J B, Choi Y H. A simple adaptive control approach for trajectory tracking of electrically driven nonholonomic mobile robots. IEEE Transactions on Control Systems Technology, 2010, 18(5):1199-1206 |
| [12] | Ren W, Beard R W. Decentralized scheme for spacecraft formation flying via the virtual structure approach. Journal of Guidance, Control, and Dynamics, 2004, 27(1):73-82 |
| [13] | Do K, Jiang Z, Pan J. Robust adaptive path following of underactuated ships. Automatica, 2004, 40(6):929-944 |
| [14] | Ghommam J, Mnif F, Derbel N. Global stabilisation and tracking control of underactuated surface vessels. IET Control Theory and Applications, 2010, 4(1):71-88 |
| [15] | Borhaug E, Pavlov A, Panteley E, Pettersen K Y. Straight line path following for formations of underactuated marine surface vessels. IEEE Transactions on Control Systems Technology, 2011, 19(3):493-506 |
| [16] | Cheah C, Wang D, Sun Y. Region-reaching control of robots. IEEE Transactions on Robotics, 2007, 23(6):1260-1264 |
| [17] | Sun Y, Cheah C. Region-reaching control for underwater vehicle with onboard manipulator. IET Control Theory and Applications, 2007, 2(9):819-828 |
| [18] | Ismail Z H, Dunnigan M W. A region boundary-based control scheme for an autonomous underwater vehicle. Ocean Engineering, 2011, 38(17-18):2270-2280 |
| [19] | Cheah C, Hou S, Slotine J. Region following formation control for multi-robot systems. In:Proceedings of the 2008 IEEE International Conference on Robotics and Automation. Pasadena, CA:IEEE, 2008. 3796-3801 |
| [20] | Cheah C C, Hou S P, Slotine J J E. Region-based shape control for a swarm of robots. Automatica, 2009, 45(10):2406-2411 |
| [21] | Ren B, Ge S S, Lee T H, Krstic M. Region tracking control for multi-agent systems with high-order dynamics. In:Proceedings of the 2013 American Control Conference. Washington, DC:IEEE, 2013. 1266-1271 |
| [22] | Zavlanos M M, Pappas G J. Controlling connectivity of dynamic graphs. In:Proceedings of the 44th IEEE Conference on Decision and Control. Seville, Spain:IEEE, 2005. 6388-6393 |
| [23] | Zavlanos M M, Jadbabaie A, Pappas G J. Flocking while preserving network connectivity. In:Proceedings of the 46th IEEE Conference on Decision and Control. New Orleans, USA:IEEE, 2007. 2919-2924 |
| [24] | Tee K P, Ge S S, Tay E H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica, 2009, 45(4):918-927 |
| [25] | Ren B, Ge S S, Tee K P, Lee T H. Adaptive neural control for output feedback nonlinear systems using a barrier lyapunov function. IEEE Transactions on Neural Networks, 2010, 21(8):1339-1345 |
| [26] | Skjetne R, Fossen T I, Kokotović P V. Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica, 2005, 41(2):289-298 |
| [27] | Ren B, Ge S S, Su C Y, Lee T H. Adaptive neural control for a class of uncertain nonlinear systems in pure-feedback form with hysteresis input. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics, 2009, 39(2):431-443 |
| [28] | Ge S S, Wang C. Adaptive neural control of uncertain MIMO nonlinear systems. IEEE Transactions on Neural Networks, 2004, 15(3):674-692 |
| [29] | Polycarpou M M, Ioannou P A. A robust adaptive nonlinear control design. Automatica, 1996, 32(3):423-427 |
| [30] | Krstic M, Kanellakopoulos I, Kokotovic P. Nonlinear and Adaptive Control Design. New York:Wiley, 1995. 139-151 |
 2014, Vol.1
2014, Vol.1 


