Recently,the localization problem of autonomous underwater vehicles (AUVs) has been attracting enormous attention because localization is acknowledged as an essential capability of an AUV while ocean exploration activities are significantly increasing worldwide[1]. The traditional techniques,such as dead-reckoning and acoustic baseline system with arrays of pre-deployed static beacons,suffer from unbounded localization errors,costly setting up,restricted operating area,etc. Further in order to decrease costs and simplify the design complexity of AUVs,the small and simple AUVs are increasingly being adopted, which make the traditional underwater localization systems unsuitable due to limited size,power and payload of AUVs while adding to the already high cost of localization systems in terms of hardware complexity and energy consumption. Therefore,a new underwater localization scheme,based on the cooperative localization between AUV and a single mobile surface vehicle,has been studied in recent years to overcome these drawbacks[2, 3, 4, 5].
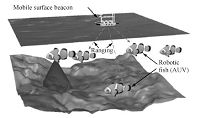
In a cooperative localization system shown in Fig. 1,mobile surface vehicle and underwater vehicles cooperate with each other to provide localization capability for AUVs. Surface vehicle can obtain its absolute position in real-time,which is broadcast for AUVs to estimate the distance between them. With the aid of these range measurements,AUVs can bound the localization errors accumulated by dead-reckoning. Because both surface vehicle and AUVs are cooperatively controlled to move as a team,operating area of AUVs is also dramatically enlarged,thanks to the mobility of surface beacon. In [5, 6],the centralized extended Kalman filter (EKF) and decentralized extended information filter are proposed for off-line and real-time cooperative localizations of AUVs with highly accurate sensors,such as Doppler velocity log (DVL). In order to perform the cooperative localization of AUVs in the absence of DVL,the approaches based on EKF,particle filter (PF) and nonlinear least squares (NLS) optimization are proposed in [2, 3]. However,the computational complexity of NLS grows over time since all the previous calculated states and observed measurements are involved in the optimization,making it unsuitable for real-time applications,such as environment monitoring[6]. In [7],Wang et al. develop the finite-horizon $H_\infty$ filtering for the online robot localization without increasing the problem size over time. However,none of these methods considers the constraints of state variable and process uncertainty which are imposed by the physical insight. In [8, 9], moving horizon estimation (MHE),a maximum a posteriori (MAP) method,is used to formulate the robot localization problem into a fixed window optimization incorporating the constraints. In both of them,the MHE is designed for two dimensional localization problem with the aid of several static beacons or landmarks.
|
Download:
|
| Fig. 1.Architecture of underwater cooperative localization. | |
Our method is also based on MHE,but it requires the availability of only single mobile beacon for three-dimensional cooperative localization problem. Since only range measurements from a single mobile beacon are used to bound the localization error of a group of AUVs,the observability,which can determine the be investigated first. In [10, 11, 12],the robot localization,should rank of observability matrix is proposed for observability analysis of linear systems or linearized nonlinear systems. However,the original localization systems are usually nonlinear and the linearization may lead to a wrong decision about observability[3]. Therefore,the observability rank condition derived from Lie derivative for nonlinear continuous time system is used in [3, 13, 14] to study the observability of robot localization. However,all these studies transform discrete time systems into continuous time systems for observability analysis with the assumption that sampling time is small enough. To the best of authors$'$ knowledge,no research has considered the observability of robot localization using the nonlinear discrete system directly. Actually,most of the localization systems are discrete-time systems. Consequently,it is worth analyzing the observability of localization in the context of its discrete representation. Another challenge is that the propagation speed of underwater acoustic communication is much slower than that of wireless signal,which results in low frequency of underwater ranging and impossibility of using wireless communication based method[15]. The high latency degrades localization accuracy or even makes the estimator divergent if no special care is taken.
To address the aforementioned problems,a novel underwater cooperative localization scheme is proposed in this paper to provide real-time localization capability for a school of robotic fish. The main contribution of this paper is twofold: 1) A straightforward method,which is able to directly analyze the observability of single beacon localization in discrete time systems,is proposed and sufficient conditions for the observability of both nonlinear system and linearized system are derived. It also analytically verifies that a nonlinear state estimation method is necessary for this localization scenario. 2) An algorithm which combines EKF and MHE to perform three-dimensional localization in real-time is developed, avoiding the unbounded rise in computations and considering physical constraints. To the best knowledge of the authors,the method proposed in this paper is the first implementation of MHE in the context of three-dimension and single beacon based localization, using inaccurate model and measurements suffering from low bandwidth and high latency.
The rest of this paper is organized as follows. Section II outlines the research problem and analyzes the observability. In Section III, the proposed localization algorithm is described. Section IV presents the simulation results to verify the feasibility and performance of the proposed algorithm. Finally,the conclusion and future work are presented in Section V.
II. LOCALIZATION WITH A SINGLE BEACON A. Problem DescriptionIn this cooperative localization system,there is a school of robotic fish (RF) and a single beacon[16]. Each RF is equipped with a low-cost pressure sensor,an inertial measurement unit (IMU) and an acoustic modem instead of the expensive and energy consuming ones,such as DVL. It can also measure ranges between surface beacon and itself by acoustic modem.
1) Kinematic model
Because the underwater RF can neither access its velocities directly
like the mobile robots using odometry or the AUVs with DVL,nor can
be modeled as accurate as its counterparts driven by propeller,the
kinematic model of AUVs used in [5, 17] is adopted with slight
change in this paper. Consider the position $\boldsymbol{s}_{k}$ and
attitude $\boldsymbol{\varphi}_{k}$ (roll,pitch and yaw) of RF in
global coordinate frame as the state $\boldsymbol{x}_{k}$ $=$
$[\boldsymbol{s}_{k}^{\rm T},\boldsymbol{\varphi}_{k}^{\rm T}]^{\rm
T}$ to be estimated at time $k$,where
\begin{align*}
\boldsymbol{s}_k=\begin{bmatrix}
x_k & y_k & z_k
\end{bmatrix}^{\rm T},
\hspace{0.1in}
\boldsymbol{\varphi}_k=\begin{bmatrix}
\phi_k & \theta_k & \psi_k
\end{bmatrix}^{\rm T}.
\end{align*}
Control input is $\boldsymbol{u}_k=[\boldsymbol{v}_{k}^{\rm T},
\boldsymbol{\omega}_{k}^{\rm T}]^{\rm T}$,where
\begin{align*}
\boldsymbol{v}_{k} =\begin{bmatrix}
u_k & \nu_k & w_k
\end{bmatrix}^{\rm T},
\hspace{0.1in}
\boldsymbol{\omega}_k=\begin{bmatrix}
p_k & q_k & r_k
\end{bmatrix}^{\rm T}
\end{align*}
are body-frame linear and angular velocities of RF respectively.
Then,under the assumption that sampling time interval is
$\Delta_T$,the process model for RF can be represented as the
following nonlinear discrete time system:
\begin{align}
\label{eq:ProbDescrip:SystemModel}
\boldsymbol{x}_{k+1} = f(\boldsymbol{x}_{k},\boldsymbol{u}_k) =
\boldsymbol{x}_{k}+\Delta_TJ(\boldsymbol{x}_{k})\boldsymbol{u}_k,
\end{align}
(1)
The system model (1) cannot provide accurate movement prediction due
to the random characteristics and unavailability of true control
input $\boldsymbol{u}_k$. Therefore,onboard IMU and pressure sensor
are employed to refine the predicted attitude and depth of RF.
However,the error of dead-reckoning increases unboundedly over
time. Then,a single beacon is introduced to reduce the uncertainty
and error of localization by providing acoustic range measurement.
In the presence of acoustic modem,IMU and pressure sensor,the
measurement model of RF with three types of measurements (range
$z_{r}$,attitude $\boldsymbol{z}_{a}$ and depth $z_{d}$) is
\begin{align}
\boldsymbol{z}_k = h(\boldsymbol{x}_{k})+\boldsymbol{\mu}_k=\begin{bmatrix}
z_{r,k} & \boldsymbol{z}_{a,k}^{\rm T} & z_{d,k}
\end{bmatrix}^{\rm
T},
\label{eq:ProbDescrip:MeasModel}
\end{align}
(2)
1) Range measurement. The single beacon broadcasts its
position periodically via an acoustic modem for RF to estimate the
range by means of time of arrival. Denote the position of single
beacon at time $k$ as $(x_{k}^b,y_{k}^b,z_{k}^b)$. Then,the
range measurement is
\begin{align}
z_{r,k} = \sqrt{(x^{b}_k-x_{k})^2+(y^{b}_k-y_{k})^2+(z^{b}_k-z_{k})^2} + \mu_{r,k}.
\label{eq:ProbDescrip:MeasModelRange}
\end{align}
(3)
2) Attitude measurement. IMU measurement is used to estimate the
attitude by the following measurement model:
\begin{align}
\boldsymbol{z}_{a,k}= {H}_{a,k}\boldsymbol{x}_k + \boldsymbol{\mu}_{a,k}
= \begin{bmatrix}
{0}_{3\times 3} & {I}_{3\times 3}
\end{bmatrix}\boldsymbol{x}_k +
\boldsymbol{\mu}_{a,k},
\label{eq:ProbDescrip:MeasModelIMU}
\end{align}
(4)
3) Depth measurement. Depth measured by pressure sensor is related
to the vertical position of RF. Then,the depth is
\begin{align}
z_{d,k}={H}_{d,k}\boldsymbol{x}_k + \mu_{d,k} =
\begin{bmatrix}
0 & 0 & 1 & {0}_{1\times 3}
\end{bmatrix}\boldsymbol{x}_k + \mu_{d,k},
\label{eq:ProbDescrip:MeasModelDepth}
\end{align}
(5)
Some powerful and precise sensors are mounted on the surface beacon vehicle to make sure that the reference position,which can be directly obtained by GPS when surfacing or estimated by simultaneous localization and mapping (SLAM) when submerged[1, 18],can be provided for the submerged RF. This heterogeneous scheme where a single beacon has many powerful sensors while no expensive equipments are deployed on the RF can substantially reduce the hardware and energy cost of the whole system,especially for a shoal with multiple RFs. In terms of the cooperative localization mechanism,several waypoints are pre-defined for the surface vehicle to pass through,during the operation. Meanwhile,AUVs are properly controlled to cooperate with surface beacon so that all of them are always kept in the ranging area of the surface beacon. As this paper mainly focuses on the localization problem,the cooperative control is simplified by controlling the vehicles passing through the waypoints.
The single beacon based multi-RF cooperative localization problem is how to simultaneously and accurately localize several RF modeled as (1) with the aid of the measurement model (2). However, because the system is nonlinear and discrete time,the inherent nonlinear and discrete features have to be considered in the subsequent observability analysis and localization algorithm design.
B. Observability AnalysisObservability which relates to localizability in the context of robot localization is a necessary but not sufficient condition. It means that the observable states can be updated by using the obtained measurements although the corresponding estimation error and error covariance may not converge,and the unobservable states can only be determined by prediction and their errors may not be bounded. Therefore,to successfully localize the robot,all the states have to be observable with respect to a given measurement model.
The criteria based on codistributions for observability of the
nonlinear discrete time system[19] is adopted to analyze the
observability and derive the sufficient condition of this single
beacon based localization directly. Consider the observation space
$\boldsymbol{\Theta}=\bigcup_{k\geq1}\boldsymbol{\Theta}_k$
constructed by the set of functions
\begin{align}
&\boldsymbol{\Theta_1} = \{h\},\nonumber\\[2mm]
&\boldsymbol{\Theta_k} = \{h\circ f_{u_1}\circ\cdots\circ f_{u_j},
1\leq j \leq k-1\},\ k\geq2,
\end{align}
(6)
For the system described above,the number of system state
variables to be tested is $6$. According to
(2) and
(6),it yields
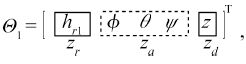
(7)
\begin{align}
\nabla \boldsymbol{\Theta_1} =\left[\begin{array}{*{20}ccccccccccc}
\dfrac{x^b-x}{h_{r1}} & \dfrac{y^b-y}{h_{r1}} & \dfrac{z^b-z}{h_{r1}} & 0 & 0 &
0\\[2mm]
0 & 0& 0& 1 & 0 & 0\\
0 & 0& 0& 0 & 1 & 0\\
0 & 0& 0& 0 & 0 & 1\\
0 & 0& 1& 0 & 0 & 0
\end{array}\right].
\end{align}
(8)
\begin{align}
\boldsymbol{\Theta_2} = \left[\begin{array}{*{20}cccccccccc}
h_{r2} & \phi +\Delta B_1& \theta +\Delta B_2 & \psi +\Delta B_3&s_3\\
\end{array}\right]^{\rm T},
\end{align}
(9)
\begin{align}
\nabla \boldsymbol{\Theta_2} =\left[\begin{array}{*{20}cccccccccc}
\dfrac{x^b-s_1}{h_{r2}} & \dfrac{y^b-s_2}{h_{r2}} & * & * & * &
*\\[2mm]
0 & 0 & * & * & * & *\\
0 & 0 & * & * & * & *\\
0 & 0 & * & * & * & *\\
0 & 0 & * & * & * & *
\end{array}\right],
\end{align}
(10)
\begin{align}
\mathcal{O}=\left[\begin{array}{*{20}c}
\dfrac{x^b-x}{h_{r1}} & \dfrac{y^b-y}{h_{r1}}\\[3mm]
\dfrac{x^b-x-\Delta_T\boldsymbol{a}^1\boldsymbol{v}}{h_{r2}} & \dfrac{y^b-y-\Delta_T\boldsymbol{a}^2 \boldsymbol{v}}{h_{r2}}
\end{array}\right].
\end{align}
(11)
\begin{align}
(y^b-y)\Delta_T\boldsymbol{a}^1\boldsymbol{v}-(x^b-x)\Delta_T\boldsymbol{a}^2
\boldsymbol{v}\neq0.
\end{align}
(12)
|
Download:
|
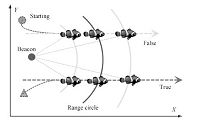
| Fig. 2. Local observability using single static beacon. | |
It is interesting to employ the local observability matrix
condition[21] to study the observability of the linearized
system again. The measurement model (2) is linearized as
\begin{align}
\boldsymbol{z}_k =
{H}_{k}\boldsymbol{x}_{k}+\boldsymbol{\mu}_k,
\end{align}
(13)
\begin{align}
{H}_{k} =\left[\begin{array}{*{20}c}
\dfrac{x^b_k-x_k}{h_{r1,k}} & \dfrac{y^b_k-y_k}{h_{r1,k}} & \dfrac{z^b_k-z_k}{h_{r1,k}} & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0\\
0 & 0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 0 & 1\\
0 & 0 & 1 & 0 & 0 & 0
\end{array}\right].
\end{align}
(14)
\begin{align}
\mathcal{O}_L=
\left[\begin{array}{*{20}c}
{H}_{k}\\
{H}_{k+1}{F}_{k}\\
\vdots\\
{H}_{k+n-1}{F}_{k+n-2}\cdots{F}_{k}\\
\end{array}\right],
\end{align}
(15)
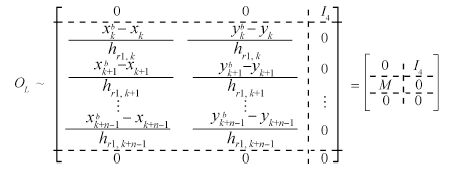
According to the principle of partitioned matrix,the rank of
$\mathcal{O}_L$ can be obtained by
\begin{align}
{\rm rank}(\mathcal{O}_L) = {\rm rank}({I}_{4}) + {\rm rank}({M}) = 4 +
{\rm rank}({M}).
\end{align}
(16)
\begin{align}
\dfrac{y^b_{k+i}-y_{k+i}}{x^b_{k+i}-x_{k+i}} \neq
\dfrac{y^b_{k+j}-y_{k+j}}{x^b_{k+j}-x_{k+j}},\ i,j\in
[0,n-1]~\text{and}~i\neq j
\end{align}
(17)
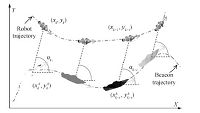
|
Download:
|
| Fig. 3.A scenario where linearized system
is
locally unobservable but original nonlinear system is observable (The relative directions $\sigma_{k+i}$ between robot and beacon remain constant during the period.) |
|
The observability analysis verifies that measurement (2) is sufficient for pose estimate of the robot if the corresponding sufficient condition for observability can be satisfied. However, the comparison of observability analysis between the nonlinear and linearized systems implies that some states which cannot be observed by a linearized observer,such as EKF,can be successfully estimated by using a nonlinear filter. Therefore,a localization algorithm based on nonlinear estimator is developed in next section for robot localization.
C. State Constraints
Some available prior knowledge of system and environment can be
applied to constrain the state variables and noises,and to
improve the estimation accuracy. The constraints usually exist in
the form of equality or inequality,e.g.,the operating area of
the robot position can be represented by a geometric model with
inequalities. Suppose the state variables,control inputs and
disturbances satisfy the following $q$ constraints:
\begin{align}
g_{i}(\boldsymbol{x},\boldsymbol{u},\boldsymbol{w})\leq0,\ i =
1,\cdots,q.
\end{align}
(18)
With the system model described above,the attitude,depth and range measurements should be fused together to conduct localization. Attitude and depth data from IMU and pressure sensor is normally obtained at high frequency. However,due to low propagation speed of the acoustic signal and the usually long distance between the AUVs,the range measurement is updated at a low rate,which hinders the direct application of MHE method.
Taking these differences into account,our proposed localization algorithm utilizes several separately designed filters to fuse data asynchronously. Specifically,the typical EKF filters are used to update the prediction using attitude and depth measurements,which serves as the dead-reckoning and compensation for the low rate range measurement. Once a range measurement is available,current position is ameliorated by a MHE based method,which can not only highly restrain the noise and smooth out the estimate but also consider the constraints on the operating environment and physical system. The reason for employing both EKF and MHE is that the real-time feature of EKF is suitable for updating measurements at a high frequency (attitude and depth) while MHE incorporates several previous range measurements at one estimate,compensating for the single range measurement at each step.
A. Prediction and Update Using Attitude and DepthPrediction and update using attitude and depth comprise the dead-reckoning for the AUVs,which estimates displacement and direction change with respect to previous pose.
1) Prediction
State $\boldsymbol{x}$ is propagated by using the model (1),and
covariance matrix ${P}$ at time $k$ is obtained by
\begin{align}
{P}_k = {F}_k{P}_{k-1}{F}_k^{\rm T}+{G}_k{Q}_k{G}_k^{\rm T},
\end{align}
(19)
IMU and pressure sensor are introduced to reduce the prediction error accumulation. Because both their measurements are acquired much faster than range measurement,the prediction is updated by attitude and depth observations at a high rate. Therefore,once an attitude or depth measurement is received,a standard EKF filter is used to update the corresponding state and covariance using (4) and (5) without the measurement noises. Because both measurement models of attitude (4) and depth (5) are linear,the observability can still hold which would be identical with nonliear analysis when EKF is used. The technical detail of EKF filter design is omitted here due to its straightforward steps.
B. MHE Based Update Using Range MeasurementWhen a range measurement $z_{r}$ is received by RF,current state propagated by dead-reckoning is updated by MHE method.
MHE can be derived in the perspective of probability theory. At time
$k$,suppose a sequence of range measurements
$\{z_{r,0},z_{r,1},\cdots,z_{r,k}\}$ has been observed from the
beginning. Then,conditional probability density function (PDF) of
state
$\{\boldsymbol{x}_{0},\boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{k}\}$
given measurements $\{z_{r,0},z_{r,1},\cdots$,$z_{r,k}\}$ at time
$k$ is:
\begin{align}
p(\boldsymbol{x}_{0},\boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{k}|z_{r,0},z_{r,1},\cdots,z_{r,k}).
\end{align}
(20)
\begin{align}
p(\boldsymbol{x}_{0},\boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{k}) =
p(\boldsymbol{x}_0)\prod_{i=0}^{k-1}p(\boldsymbol{x}_{i+1}|\boldsymbol{x}_i).
\end{align}
(21)
\begin{align}
p(z_{r,0},\cdots,z_{r,k}|\boldsymbol{x}_{0},\cdots,\boldsymbol{x}_{k})
=
\prod_{i=0}^{k}p_{\mu_{r,i}}(z_{r,i}-h(\boldsymbol{x}_{i})).
\end{align}
(22)

|
Download:
|
| Fig. 4.Localization trajectories of dead-reckoning,EKF and MHE with static or mobile surface beacons. | |
Since $p(z_{r,0},\cdots,z_{r,k})$ is for normalization,we have \begin{align*} & p(\boldsymbol{x}_{0},\cdots,\boldsymbol{x}_{k}|z_{r,0},\cdots,z_{r,k} )\propto \\ &\qquad p(\boldsymbol{x}_0) \prod_{i=0}^{k}p_{\mu_{r,i}}(z_{r,i}-h(\boldsymbol{x}_{i}))\prod_{i=0}^{k-1}p(\boldsymbol{x}_{i+1}|\boldsymbol{x}_i). \end{align*} Thus,under the assumptions that process noises $\boldsymbol{w}$ are mutually independent,MAP can be derived: \begin{align*} &\arg\max_{\boldsymbol{x}_{0},\cdots,\boldsymbol{x}_{k}} p(\boldsymbol{x}_{0},\cdots,\boldsymbol{x}_{k}|z_{r,0},\cdots,z_{r,k})=\\ &\qquad \arg\max_{\boldsymbol{x}_{0},\cdots,\boldsymbol{x}_{k}} \log p(\boldsymbol{x}_0) + \sum_{i=0}^{k}\log p_{\mu_{r,i}}(z_{r,i}-h(\boldsymbol{x}_{i}))+\\ &\sum_{i=0}^{k-1}\log p_{\boldsymbol{w}_i}(\boldsymbol{x}_{i+1}-f(\boldsymbol{x}_{i},\boldsymbol{u}_{i})). \end{align*} Because $\boldsymbol{w}$ and $\boldsymbol{\mu}$ are normal distributions,it can be rewritten as \begin{align*} & \arg\min_{\boldsymbol{x}_{0},\cdots,\boldsymbol{x}_{k}} \Phi_k(\{\boldsymbol{x}\}_{0}^k) =\arg\min_{\boldsymbol{x}_{0},\cdots,\boldsymbol{x}_{k}} \|\boldsymbol{x}_{0} - \boldsymbol{\hat{x}}_{0}\|_{\boldsymbol{\Pi}_{0}}^2 +\\ &\qquad \sum_{i=0}^{k}\|z_{r,i}-h(\boldsymbol{x}_{i})\|_{R_{r}}^2+\sum_{i=0}^{k-1}\|\boldsymbol{x}_{i+1}-f(\boldsymbol{x}_{i},\boldsymbol{u}_{i})\|_{\boldsymbol{Q}_{i}}^2, \end{align*} where $\|z\|_{A}^2 = z^{\rm T}A^{-1}z$,and $p(\boldsymbol{x}_0)\sim {\rm N}(\boldsymbol{\hat{x}}_{0},\boldsymbol{\Pi}_{0})$ is prior knowledge on the initial state. Since the range measurements obtained from the beginning are all incorporated into this optimization problem to calculate all the states $\{\boldsymbol{x}\}_{0}^k=$ $\{x_0$,$\cdots$,$x_k\}$ at time $k$, both the number of state variables and computational complexity increase over time. Due to this,it is impossible to use MAP for long-term or real-time applications.
MHE method can overcome the drawbacks of MAP. Consider the preceding
MAP derivation and MHE theory in [23]. The objective function
$\Phi_k(\{\boldsymbol{x}\}_{0}^k)$ of MAP can be represented by
separating the time interval into two sections $\{t: 0\leq t \leq
k-N\}$ and $\{t:k-N+1\leq t \leq k\}$:
\begin{align*}
\Phi_k(\{\boldsymbol{x}\}_{0}^k) =&\sum\limits_{i=k-N}^{k-1}\|\boldsymbol{w}_i\|_{\boldsymbol{Q}_{i}}^2+
\sum\limits_{i=k-N+1}^{k}\|\mu_{r,i}\|_{R_r}^2+\\
&\sum\limits_{i=0}^{k-N-1}\|\boldsymbol{w}_i\|_{\boldsymbol{Q}_{i}}^2+\sum\limits_{i=0}^{k-N}\|\mu_{r,i}\|_{R_r}^2 +
\|\boldsymbol{x}_0-\hat{\boldsymbol{x}}_0\|_{\boldsymbol{\Pi}_{0}}^2,
\end{align*}
where $N$ is the size of estimation window. Since the first two
items of this equation only rely on the states
$\{\boldsymbol{x}\}_{k-N}^{k}$ and the range measurements
$\{z_{r}\}_{k-N+1}^{k}$,the optimization can be transformed into a
problem with fixed-window size,as shown in Fig. 5,by
approximating the rest part of the objective function with an
arrival cost. By denoting the set $\{\boldsymbol{w}\}_{k-N}^{k-1}$
as the input disturbances from time $k-N$ to time $k-1$,the states
of interest can be calculated by $\boldsymbol{x}_{k-N}$ and
$\{\boldsymbol{w}\}_{k-N}^{k-1}$,thanks to process model (1).
Therefore,MHE considering the constraints (18) at time $k$ is
\begin{align}
&\arg\min_{\boldsymbol{x}_{T_s},\{\boldsymbol{w}\}_{T_s}^{k-1}}
{\textstyle\sum\limits_{i=T_s}^{k-1}}\|\boldsymbol{w}_i\|_{\boldsymbol{Q}_{i}}^2+{\textstyle\sum\limits_{i=T_s+1}^{k}}\|\mu_{r,i}
\|_{R_r}^2 + \mathcal{Z}_{T_s}(\boldsymbol{x}_{T_s}),\nonumber\\
&\ \text{s.t.}\quad
g_{i}(\boldsymbol{x},\boldsymbol{u},\boldsymbol{w})\leq0,\quad i =
1,\cdots,q,
\end{align}
(23)
\begin{align}
\mathcal{Z}_{T_s}(\boldsymbol{x}_{T_s})=\|\boldsymbol{x}_{T_s}-\hat{\boldsymbol{x}}_{T_s}\|^2_{\boldsymbol{P}_{T_s}^{-1}},
\end{align}
(24)

|
Download:
|
| Fig. 5. MHE with fixed-size window. | |
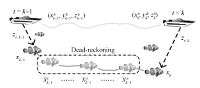
|
Download:
|
| Fig. 6.System description between two range measurements. | |
In this section,the performance of the proposed localization algorithm is evaluated through simulation. The simulation is conducted by using robot operating system (ROS). For comparison, the localization trajectories and errors of dead-reckoning,EKF and MHE (the proposed method combining EKF update of attitude and depth) in three different scenarios are presented and analyzed. The 52m $\times$ 52m $\times$ 20m boundary in Fig. 4(a) shows the operating field with channel,obstacles and starting and ending positions. It takes about $20$ minutes for the robotic fish to travel the whole trip in simulation. According to the specification of Tritech micron acoustic modem,the frequency of range update is set to be $1$Hz and $R_r = (0.2{\rm m})^2$. The frequencies of IMU and pressure sensor are $100$Hz with ${R}_a$ $=$ $(0.36\text{rad/s})^2I$ and $R_d = (0.2{\rm m})^2$. Note that different localization algorithms are all fed with the same control input and observation in each trial.
A. Observability AnalysisIn order to verify the observability analysis proposed in Section II-B,a scenario where the relative direction between mobile beacon and robot is always $90^{\circ}$ during the motion is considered, see the trajectories of ground truth and beacon in Fig. 8(b). It is easy to prove that condition (12) is satisfied yet condition (17) is not.
B. Observability AnalysisIn order to verify the observability analysis proposed in Section II-B,a scenario where the relative direction between mobile beacon and robot is always $90^{\circ}$ during the motion is considered, see the trajectories of ground truth and beacon in Fig. 8(b). It is easy to prove that condition (12) is satisfied yet condition (17) is not.
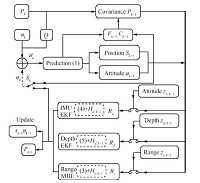
|
Download:
|
| Fig. 7.The structure diagram of the algorithm. | |
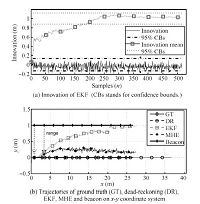
|
Download:
|
| Fig. 8.Localization results under the scenario where the ob- servabilities of EKF and MHE are different. | |
Innovation of EKF and localization trajectories are presented in Fig. 8. Innovation performance in Fig. 8(a) validates that the designed EKF filter is superior and consistent,ensuring itself as ideal for comparison. It is can be seen from Fig. 8(a) that the innovation sequence has zero mean and most of the innovations are within the $\pm 2\sigma$ confidence bounds. As expected,the averaged innovation,which should follow $\chi^2$ distribution in the identical degree of freedom with measurement,also converges to $1$ and falls within the $\pm 2\sigma$ confidence interval. Note that the measurement here is only the range since IMU and altimeter measurements are fused in prediction. As shown in Fig. 8(b),even this EKF is well designed,it still cannot estimate the position of robot appropriately. In contrast,the estimate of MHE converges to ground truth of the robot with bounded error. The reason is because the linearized system in this scenario is not observable while the original nonlinear one is. Therefore,the robot positions in this unobservable region for EKF can still be recovered by MHE.
C. Localization AccuracyFig. 4 shows the ground truth of RF and the corresponding localization trajectories using dead-reckoning,EKF and MHE with the aid of single static beacon,mobile beacon and mobile beacon with constraints,respectively. In Fig. 4(a),which is produced based on a single static beacon,the result of dead-reckoning (dashed line with circles) gradually diverges from the ground truth (solid line), which means that the errors on $x$ and $y$ axes are accumulated. In contrast,the result of the EKF which fuses the range measurements from the static beacon is accurate in certain periods with the bounded errors although it is worse than that of the MHE (see localization errors in Fig. 9(a)). The reason for this can be explained as only single range observation is available for each step and the static beacon cannot improve the observability effectively. EKF method which only utilizes current range observation in the update cannot acquire sufficient range information,resulting in ineffective estimate of the position. Moreover,the linearization of nonlinear system model also degrades the accuracy of estimation. In contrast,since several previous range measurements can be used in one estimation and the nonlinear model is adopted in MHE,the proposed MHE method is able to converge to the ground truth with high accuracy. However,as shown in the enlargements in Fig. 4(a),the trajectory of MHE crosses the boundary occasionally,which is not reasonable in reality.
With the means of a single surface mobile beacon,the localization accuracy of EKF is improved as described in Figs.4(b) and 9(b),which validates that the beacon mobility increases the observability. However,the performance of EKF in terms of localization accuracy is still inferior to MHE. The reason is that several range measurements used in one estimate of MHE can highly restrict the possible positions of AUV to a small region in three dimensions,while the single range in each update of EKF can only give a large spherical region in three dimensions. Although the mobile beacon is employed,the problem of MHE that trajectory is beyond the boundary has not been solved yet. After introducing the boundary constraints into MHE,all the estimates are confined in the channel as can be seen from the magnified parts in Fig. 4(c). However, the positions estimated by EKF cannot always be located in the operating area,and the constraints on operating area cannot be easily imposed in the classic EKF method. By these numerical evaluations,it verifies that the proposed MHE method can produce more accurate localization estimation than EKF in the context of single beacon and it is more suitable for the single beacon based localization. Moreover,its localization accuracy is robust to various disturbances.

|
Download:
|
| Fig. 9.Localization errors of dead-reckoning,EKF and MHE with single static or mobile surface beacon. | |
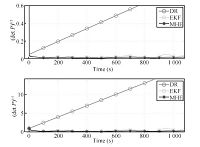
The overall uncertainty of the position estimate in three dimensions is proportional to the square root of the determinant of the covariance on $x,y,z$,i.e.,$\sqrt{\det P_{x,y,z}}$. According to this relation,the spatial uncertainties of dead-reckoning,EKF and MHE methods in one trial are presented in Fig. 10. It can be seen that,as expected,the uncertainty of dead-reckoning grows monotonically without bound while that of EKF and MHE does not increase over time in both $x,y,z$ and $x,y$ with the aid of range measurements. The reason why uncertainty of dead-reckoning is unbounded is that there is no position update in dead-reckoning and all the estimates are based on system model and inertial sensors. But the uncertainties of EKF and MHE methods are restrained,thanks to the range measurements from beacon. The initial large uncertainties of EKF and MHE are also decreased and converged. Again MHE is still better than EKF if the figure is rescaled. Uncertainties of orientation of three methods are all bounded, thanks to the IMU,which can be analyzed similarly.
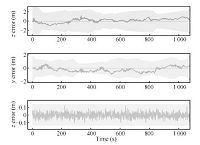
Corresponding to Fig. 10,Fig. 11 shows the localization errors in $x,y,z$ of MHE against their respective $\pm 3\sigma$ confidence intervals. All the errors are within their lower and upper confidence bounds with extra allowance,which indicates that the estimation of this MHE based localization is reliable and the proposed algorithm is effective.
V. CONCLUSIONSCooperative localization is a feasible solution to multi-agent localization problem. A three-dimensional single beacon based underwater localization algorithm which combines the EKF and MHE is proposed in this paper. It uses the dead-reckoning and range measurements to provide the accurate location with bounded error for the small AUVs,which have constrained size and limited sensors. The observability of single beacon based localization is analyzed in the context of the nonlinear discrete time system, producing the sufficient condition for single beacon based localization. The reasons why a nonlinear state estimation has to be adopted are also given. Compared with EKF,the high localization accuracy and effectiveness of the proposed approach are validated by simulations in different scenarios. Our future work will focus on implementing the proposed method on our robotic fish to perform real-time cooperation and environment mapping.
|
Download:
|
| Fig. 10.Overall uncertainty in position $x$,$y$,$z$ and $x$,$y$ only. | |
|
Download:
|
| Fig. 11.Errors in $x$,$y$,$z$ and 3$\sigma$ confidence intervals. | |
We would like to thank Robin Dowling and Ian Dukes for their technical support during the research.
| [1] | Chen L, Wang S, McDonald-Maier K, Hu H S. Towards autonomous localization and mapping of AUVs:a survey. International Journal of Intelligent Unmanned Systems, 2013, 1(2):97-120 |
| [2] | Papadopoulos G, Fallon M F, Leonard J J, Patrikalakis N M. Cooperative localization of marine vehicles using nonlinear state estimation. In:Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, China:IEEE, 2010. 4874-4879 |
| [3] | Fallon M F, Papadopoulos G, Leonard J J, Patrikalakis N M. Cooperative AUV navigation using a single maneuvering surface craft. The International Journal of Robotics Research, 2010, 29(12):1461-1474 |
| [4] | Webster S E, Eustice R M, Singh H, Whitcomb L L. Preliminary deep water results in single-beacon one-way-travel-time acoustic navigation for underwater vehicles. In:Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. St. Louis, USA:IEEE, 2009. 2053-2060 |
| [5] | Webster S E, Eustice R M, Singh H, Whitcomb L L. Advances in singlebeacon one-way-travel-time acoustic navigation for underwater vehicles. In:Proceedings of the 2010 IEEE/OES Autonomous Underwater Vehicles. Monterey, CA:IEEE, 2010. 1-8 |
| [6] | Lu B W, Oyekan J, Gu D B, Hu H S, Nia H F G. Mobile sensor networks for modelling environmental pollutant distribution. International Journal of Systems Science, 2011, 42(9):1491-1505 |
| [7] | Wang Z D, Dong H L, Shen B, Gao H J. Finite-horizon H∞ filtering with missing measurements and quantization effects. IEEE Transactions on Automatic Control, 2013, 58(7):1707-1718 |
| [8] | Simonetto A, Balzaretti D, Keviczky T. A distributed moving horizon estimator for mobile robot localization problems. In:Proceedings of the 18th IFAC World Congress. Milan, Italy:IFAC, 2011. 8902-8907 |
| [9] | Pillonetto G, Aravkin A, Carpin S. The unconstrained and inequality constrained moving horizon approach to robot localization. In:Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, China:IEEE, 2009. 3830-3835 |
| [10] | Gadre A S, Stilwell D J. A complete solution to underwater navigation in the presence of unknown currents based on range measurements from a single location. In:Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton, Canada:IEEE, 2005. 1420-1425 |
| [11] | Gadre A. Observability Analysis in Navigation Systems with an Underwater Vehicle Application[Ph. D. dissertation], Virginia Polytechnic Institute and State University, Virginia, 2007 |
| [12] | Huang G P, Trawny N, Mourikis A I, Roumeliotis S I. Observabilitybased consistent EKF estimators for multi-robot cooperative localization. Autonomous Robots, 2011, 30(1):99-122 |
| [13] | Martinelli A, Siegwart R. Observability analysis for mobile robot localization. In:Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton, Canada:IEEE, 2005. 1471-1476 |
| [14] | Antonelli G, Arrichiello F, Chiaverini S, Sukhatme G. Observability analysis of relative localization for AUVs based on ranging and depth measurements. In:Proceedings of the 2010 IEEE International Conference on Robotics and Automation. Alaska, USA:IEEE, 2010. 4276-4281 |
| [15] | Xu X M, Chen Y, Xu W Y, Gong F. An efficient algorithm for mobile localization in sensor networks. International Journal of Automation and Computing, 2012, 9(6):594-599 |
| [16] | Wang S, Chen L, Hu H S, Xue Z B, Pan W. Underwater localization and environment mapping using wireless robots. Wireless Personal Communications, 2013, 70(3):1147-1170 |
| [17] | Hernández E, Ridao P, Ribas D, Batlle J. MSISPIC:a probabilistic scan matching algorithm using a mechanical scanned imaging sonar. Journal of Physical Agents, 2009, 3(1):3-12 |
| [18] | Ribas D, Ridao P, Neira J, Tardos J. SLAM using an imaging sonar for partially structured underwater environments. In:Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing, China:IEEE, 2006. 5040-5045 |
| [19] | Albertini F, DAlessandro D. Observability and forward-backward observability of discrete-time nonlinear systems. Mathematics of Control, Signals and Systems, 2002, 15(4):275-290 |
| [20] | Antonelli G, Caiti A, Calabro V, Chiaverini S. Designing behaviors to improve observability for relative localization of AUVs. In:Proceedings of the 2010 IEEE International Conference on Robotics and Automation. Alaska, USA:IEEE, 2010. 4270-4275 |
| [21] | Chen Z. Local observability and its application to multiple measurement estimation. IEEE Transactions on Industrial Electronics, 1991, 38(6):491-496 |
| [22] | Hartley R, Zisserman A. Multiple View Geometry in Computer Vision. Cambridge:Cambridge University Press, 2000 |
| [23] | Rao C V, Rawlings J B, Mayne D Q. Constrained state estimation for nonlinear discrete-time systems:stability and moving horizon approximations. IEEE Transactions on Automatic Control, 2003, 48(2):246-258 |
 2014, Vol.1
2014, Vol.1 


