2. Access Linnaeus Centre, School of Electrical Engineering, Royal Institute of Technology, Stockholm, Sweden;
3. Charles L. Brown Department of Electrical and Computer Engineering, University of Virginia, Charlottesville VA 22904-4743, USA
Control of multi-agent systems has been an area of intensive research in recent years. Indeed,multi-agent systems find applications in military operations,search and rescue, environment monitoring,commercial cleaning,material handling, and homeland security,among others. Distributed cooperative control of a multi-agent system utilizes only neighbor-to-neighbor information to generate control input to each agent. To achieve cooperation,agents must share information with other members in a team via communication. Among the distributed cooperative control schemes,consensus algorithms have been studied extensively[1, 2, 3, 4, 5, 6, 7, 8]. In particular,consensus algorithms have been studied for single-integrator dynamics in the context of undirected and directed information exchange[6]. Consensus with a constant leader and a switching undirected network topology was addressed in [7]. Similar problems were also studied in [8, 9] under a fixed directed network topology.
The above references consider the situation where only a single leader or no leader is present. However,in practical applications, there might exist multiple leaders among these agents,and the concept of multiple leaders was introduced in [10, 11, 12]. In particular,[12] proposed a stop-and-go strategy to drive a collection of mobile agents to the convex polytope spanned by multiple leaders,stationary or moving. In [13],a leader-based containment control strategy is introduced for multiple unicycle agents. It was shown that the leaders converge to a desired formation and the followers converge to the convex hull of the leaders$'$ final positions.
While many theoretical results have been obtained on containment control,few have been applied on an experimental platform, especially when collision avoidance behavior is also considered. The main purpose of this paper is to demonstrate experimentally the distributed cooperative control algorithms with containment and group dispersion on a multiple wheeled mobile robot platform for the case of dynamic leaders. Each of these mobile robots is modeled by a double integrator linear system. In particular,we will first briefly review the experimental platform setup originally introduced in [14],where experimental results on a distributed control algorithm were presented for the case of stationary leaders. We will then present a control algorithm with containment and group dispersion behaviors in the presence of multiple dynamic leaders, where velocities of all the leaders are assumed to be identical. A control algorithm is proposed for multiple double integrators linear systems under a fixed network topology. Each follower is shown to be driven to converge to the convex hull spanned by the leaders and to move with the same final velocity as the leaders. In the mean time, the collision avoidance is ensured during the movement. Both simulation results and experimental results on the multi-robot platform are provided to validate the theoretical results.
Similar containment control problem has been considered in [15, 16, 17]. However,there are many fundamental differences between our work and the the results in [15, 16, 17]. The dynamics of each agent in [15, 16, 17] is represented by a single integrator,and the communication topologies are time dependent,for example,the communication topologies in [15] are random switching topologies. In this paper,the dynamics of each agent is that of a double integrator,which is essentially an unstable system. Also,the communication topology is determined by the relative distance.
The remainder of this paper is organized as follows. The experimental platform is introduced in Section II. Section III gives the mathematical preliminaries for the distributed cooperative control. In Section IV,we present a containment and group dispersion control algorithm for multiple dynamic leaders with several simulation and experimental results. Finally,Section V draws the conclusion of the paper.
II. MULTI-ROBOT EXPERIMENTAL PLATFORM A. Experimental Platform SetupIn this section,we will briefly introduce the multi-robot experimental platform originally introduced in [14]. The testbed includes two Miabot Pro robots and three Miabot classic robots as shown in Fig. 1. The Pro robots and the classic robots are similar in their functionalities. Each robot has a differential-drive system with a rear caster,high precision wheel encoders,and eight sonar units positioned around it. The robots can calculate their positions and orientations based on the encoders. The eight sonar units can be used for localization and detection of obstacles. Besides,a base station personal computer with Bluetooth USB adapter is used in the experimental platform.

|
Download:
|
| Fig. 1.The multi-robot experimental platform. | |
In order to control multiple mobile robots under various network topologies,control software was developed to emulate a fixed or changing network topology. The control platform can be divided into two layers[18]. The top layer is responsible for network topology setting,control algorithm implementation,and bidirectional communication with the onboard micro-controller. The bottom layer is responsible for sensor data acquisition and motion control.
B. Wheeled Mobile Robot ModelIn this section,we review the wheeled mobile robot model from [19]. The wheeled mobile robots$'$ motion is described by \begin{eqnarray*} \label{eq:robot dynamics state} \!\!\left \{\begin{array}{*{20}l} \dot p_{xoi}=v_i\cos(\theta_i),\cr \dot p_{yoi}=v_i\sin(\theta_i),\cr \dot \theta_i=\omega_i,\cr \dot v_i=\dfrac{F_i}{m_i},\cr \dot \omega_i=\dfrac{\tau_i}{J_i}, \end{array}\right. \end{eqnarray*} where $(p_{xoi}(t),p_{yoi}(t)) \in {\bf R}^2 $ and $\theta_i(t) \in \bf R$ denote respectively the center coordinate and the heading angle of the $i$th robot; $v_i$ and $\omega_i$ are respectively the linear and rotational velocities of the $i$th robot; $\tau_i$, $F_i$,$m_i$ and $J_i$ are respectively the motor torque,the driving power,the mass and the moment of inertia of the $i$th robot.
Define $$p_{xi}=p_{xoi}+l\cos(\theta_i),$$ $$p_{yi}=p_{yoi}+l\sin(\theta_i),$$ where $(p_{xi}(t),p_{yi}(t))$ is the coordinate of the heading point and $l=0.07$m is the constant length between the robot center and the heading point.
Letting \begin{align*} \left[\begin{array}{cc} F_i \\ \tau_i \end{array}\right] =& \left[\!\!\begin{array}{cc} \dfrac{\cos(\theta_i)}{m_i}&-\dfrac{l\sin(\theta_i)}{J_i}\\[3mm] \dfrac{\sin(\theta_i)}{m_i}&\dfrac{l\cos(\theta_i)}{J_i} \end{array} \!\!\right]^{-1}\times \\[3mm] & \left[\!\!\begin{array}{c}\bar{v}_{xi}+v_i\omega_i\sin(\theta_i) +l\omega_i^2\cos(\theta_i) \\ \bar{v}_{yi}-v_i\omega_i\cos(\theta_i)+l\omega_i^2\sin(\theta_i)\end{array} \!\!\right], \end{align*} we have that \begin{eqnarray*} \label{robot double integrator dynamics model} \left[ \begin{array}{cc} \ddot p_{xi} \\ \ddot p_{yi} \end{array} \right]=\left[ \begin{array}{cc} \bar{v}_{xi} \\ \bar{v}_{yi} \end{array} \right], \end{eqnarray*} which represents the dynamics of a double integrator system. We can then use $p_{xi}$,$p_{yi}$,$\dot p_{xi}$ and $\dot p_{yi}$ as the state variables. Therefore,we transform the system dynamics to that of double integrators,on which we will focus in the later discussion.
III. MATHEMATICAL BACKGROUND A. Notions in Graph TheoryConsider a group of $n+m$ agents,including $n$ follower robots and $m$ leader robots. The interaction among these agents is modeled by a directed graph $\mathcal{G}=(\mathcal{V},\mathcal {E})$,where $\mathcal{V}$ $=$ $\{\nu_1$,$\nu_2$,$\cdots$,$\nu_{n+m}\}$ is a set of nodes each representing an agent and $\mathcal {E} \subseteq \mathcal {V} \times \mathcal {V}$ is a set of ordered pairs of nodes.
An edge,denoted as $(\nu_i,\nu_j)$, indicates that node $\nu_j$ has access to the state information of node $\nu_i$. An undirected graph is such that $(\nu_j,\nu_i)\in \mathcal {E}$ implies $(\nu_i,\nu_j)\in \mathcal{E}$.
A directed path is a sequence of edges of the form $(\nu_{i_1}$, $\nu_{i_2})$,$(\nu_{i_2},\nu_{i_3}),\cdots$.
The interaction graph can be mathematically represented by the adjacency matrix $\mathcal{A} = [a_{ij}] \in {\bf R}^{(n+m) \times (n+m)}$,which is defined such that $a_{ij}>0$ when $(\nu_j,\nu_i)\in\mathcal{E}$ and $a_{ij}=0$ otherwise. A Laplacian matrix $\mathcal{L}$ associated with $\mathcal{A}$ is defined as $l_{ii}=\sum_{j\neq i}a_{ij}$ and $l_{ij}=-a_{ij}$, where $j\neq i$. Here we have assumed that $a_{ii}=0$ for all $i=1,2,\cdots,n+m$.
B. Definitions and Assumption
${\bf Definition 1.}$ Suppose that there are $n$ follower robots,
labeled respectively as $\nu_1$ to $\nu_n$,and described by the
double-integrator dynamics as
\begin{align}
\label{eq:double-integrator dynamics state} &\dot x_i(t)=v_i(t),
\nonumber\\
&\dot v_i(t)=u_i(t),\quad i=1,2,\cdots,n,
\end{align}
(1)
${\bf Definition 2.}$ The group of followers and the group of leaders are denoted as $F=\{\nu_1,\nu_1,\cdots,\nu_n\}$ and $L=\{\nu_{n+1}$,$\nu_{n+2},\cdots,\nu_{n+m}\}$,respectively. Consequently,$\mathcal{G}=(L \cup F$,$\mathcal{E})$,where $\mathcal{E}$ is defined in Definition 3 below.
${\bf Definition 3.}$ The neighbors of a follower $\nu_i$ are defined as \[N_i=\{\nu_{j}:(\nu_{j},\nu_{i}) \in \mathcal {E}\},\] where $\mathcal{E}=\left \{(\nu_j,\nu_i)\in \mathcal {V} \times F: \|x_i-x_j\|\le r\right\}$ for some sensing radius $r>0$.
${\bf Definition 4.}$ The convex hull ${\rm co}\{X\}$ of a set $X=\{x_1$,$x_2$,$\cdots$,$x_k\}$ is defined as \[{\rm co}\{X\} = \left\{\sum_{i=1}^{k}\alpha_i x_i : x_i \in X,\alpha_i \geq 0,\sum_{i=1}^{k} \alpha_i=1\right\}.\]
${\bf Definition 5.}$ We use $\varphi_i$ to describe the distance between follower $\nu_i$ and the convex hull spanned by the leaders,where \[ \varphi_i=\inf\left\{\|x_i-y\|: y \in{\rm co}\left\{x_j,\nu_j \in L\right\}\right\}. \]
The sum of the distances from all the followers to the convex hull of the leaders is then given by $\varphi=\sum_{i=1}^{n}\varphi_i$.
${\bf Assumption 1.}$ At each time instant,each follower is connected to at least one leader through a path.
IV. DISTRIBUTED CONTROL WITH CONTAINMENT AND GROUP DISPERSION BEHAVIORSIn this paper,we focus on the case of leaders with a constant identical velocity. Therefore the shape of the convex hull formed by the leaders is fixed. The goal here is to drive the positions of the follower robots towards the convex hull spanned by the leader robots while guaranteeing collision avoidance during the movement. Meanwhile,the velocities of the followers will converge to that of the dynamic leaders.
A. Distributed Containment Control
Motivated by [14],we propose the following control law for each
follower $\nu_i\in F$,
\begin{align}
u_i=&-k_p\left(\sum_{j=1}^{n+m}\frac{\partial V_{ij}}{\partial x_i}
+\sum_{j=1}^{n+m} a_{ij}(x)(x_i-x_j)\right)-\nonumber\\
&\ k_d(\dot{x}_i-\dot{x}_d),
\end{align}
(2)
Note that the term $-\delta\sum_{j=1}^{n+m} \frac{\partial V_{ij}}{\partial x_i}$ is used to guarantee the group dispersion and the term $-\delta\sum_{j=1}^{n+m} a_{ij}(x_i-x_j)$ is used to drive the positions of the followers towards the convex hull formed by the leaders. The term $-k(\dot{x}_i-\dot{x}_d)$ guarantees that the velocity of the follower matches that of the leaders. By expanding the Kronecker product,we have \begin{eqnarray*} (\mathcal{L} \otimes I_p)\left[ \begin{array}{cc} x_f \\ x_l \end{array} \right] =\left[ \begin{array}{cc} \mathcal{T} \otimes I_p & \mathcal{T}_d \otimes I_p \\ 0_{pm \times pn} & 0_{pm \times pm} \end{array} \right] \left[ \begin{array}{cc} x_f \\ x_l \end{array} \right], \end{eqnarray*} where $\mathcal{T} \in {\bf R}^{n \times n}$,$\mathcal{T}_d \in {\bf R}^{n \times m}$,$x_f=[x_1^{\rm T},x_2^{\rm T},\cdots, x_{n}^{\rm T}]^{\rm T}$ $\in$ ${\bf R}^{pn}$,$x_l=[x_{n+1}^{\rm T}, x_{n+2}^{\rm T},\cdots,x_{n+m}^{\rm T}]^{\rm T} \in {\bf R}^{pm}$. Also define \begin{align*} x_d=& \left[x_{d1}^{\rm T},x_{d2}^{\rm T},\cdots,x_{dn}^{\rm T}\right]^{\rm T}=\\ & -(\mathcal{T}^{-1} \otimes I_p) (\mathcal {T}_d \otimes I_p)x_l \in {\bf R}^{pn}. \end{align*} Then we have \[\mathcal{T} \otimes I_px_f + \mathcal {T}_d \otimes I_px_l = \mathcal{T} \otimes I_p(x_f-x_d).\]
${\bf Lemma 1}$[20]. $\mathcal {T}$ is positive-definite if $\mathcal {G}$ satisfies Assumption 1. In addition,each entry of $-\mathcal {T}^{-1} \mathcal {T}_d$ is nonnegative and the sum of each row of $-\mathcal {T}^{-1} \mathcal {T}_d$ is equal to one. Furthermore, \[-\mathcal{T}^{-1} \mathcal{T}_d \otimes I_p x_l \in {\rm co}\{x_j,\nu_j \in L\}.\] Also note that $-\mathcal{T}^{-1} \mathcal{T}_d = 1$ when $m=1$.
${\bf Theorem 1\bf.}$ Suppose that Assumption 1 holds and $\|x_i(0)-x_j(0)\| > d_1$,$\forall \nu_i,\nu_j \in \mathcal {V}$, $i \neq j$.
Consider the group of follower agents whose dynamics are described by double integrator (1) and are under %the influence of the control laws (2). Then,
1) $\dot x_i(t) \rightarrow \dot{x}_d$,$\forall\nu_i \in F $,as $t\rightarrow \infty$;
2) $\|x_i(t)-x_j(t)\| > d_1$,$\forall\nu_i,\nu_j \in \mathcal {V}$,$i \neq j$;
3) $\varphi$ is ultimately bounded.
${\bf Proof.}$ We construct a Lyapunov function candidate as \begin{align*} U=&\ \frac{1}{2}\sum_{i=1}^{n}{(\dot{x}_i-\dot{x}_d)}^2+k_p\sum_{i=1}^{n}\sum_{j=n+1}^{n+m}V_{ij} +\frac{k_p}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}V_{ij}+\\ &\ \frac{k_p}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}Q_{ij}+k_p\sum_{i=1}^{n}\sum_{j=n+1}^{n+m}Q_{ij}, \end{align*} where $V_{ij}$ is defined in Section IV-A and $Q_{ij}$ is defined below: \begin{align*} Q_{ij}=\begin{cases} \dfrac{(2r^2-\|x_i-x_j\|^2)(\|x_i-x_j\|^2)}{4},&d_1<\|x_i - x_j\|\leq r,\notag\\[2mm] \dfrac{r^4}{4},& \|x_i - x_j\|> r.\notag \end{cases} \end{align*}
Then we have
\begin{equation}
\label{eq:frac qij}
\frac{\partial Q_{ij}}{\partial x_i}=a_{ij}(x_i-x_j).
\end{equation}
(3)
We next proceed to analyse the properties of the closed-loop system.
1) Velocity matching analysis
The fact that $\dot{U} \leq 0$ implies that $U(t)$ is bounded for $t$ $\geq$ $0,$ and hence $\|\dot{x}_i-\dot{x}_d\|$,$V_{ij} $ and $ Q_{ij}$ are all bounded for all $\nu_i,\nu_j \in \mathcal {V}$. The boundedness of $V_{ij}$ and $Q_{ij}$ guarantees the boundedness of $\frac{\partial V_{ij}}{\partial x_i}$ and $\frac{\partial Q_{ij}}{\partial x_i}$. From (3),we have that $\sum_{j=1}^{n+m}\frac{\partial V_{ij}}{\partial x_i} +\sum_{j=1}^{n+m} a_{ij}(x)(x_i-x_j) $ is bounded. Therefore,we know that the control input $u_i$,as given in (2),is bounded. From the double integrator dynamics (1) and control law (2),we have \begin{align*} \dot v_i=&\ u_i= \\ &-k_p\left(\sum_{j=1}^{n+m}\frac{\partial V_{ij}}{\partial x_i}+\sum_{j=1}^{n+m} a_{ij}(x_i-x_j)\right) - k_d(\dot{x}_i-\dot{x}_d). \end{align*}
It follows that $\dot v_i$ is bounded,which implies that $\ddot U$ is bounded and $\dot U$ is uniformly continuous. Then,by Barbalat$'$s Lemma,we have that $\dot U(t) \rightarrow 0$ as $t \rightarrow \infty$,and hence $\dot{x}_i\rightarrow \dot{x}_d$ for all $\nu_i\in F$ as $t \rightarrow \infty $,which indicates that all followers achieve velocity matching.
2) Group dispersion analysis
From the fact that $U(t)$ is bounded,we get that $\|x_i - x_j\| $ is bounded for all $\nu_i,\nu_j \in \mathcal {V}$. By the definition of $V_{ij}$,the fact that $\|x_i(0)-x_j(0)\| > d_1$ implies $\|x_i(t)-x_j(t)\| > d_1$,$\forall \nu_i,\nu_j$ $\in$ $\mathcal {V}$,$i \neq j $,which demonstrates that the agents will keep group dispersion throughout the movement.
3) Containment boundedness analysis
From the fact that $\dot{x}_i \rightarrow \dot{x}_d$, $\forall\nu_i\in F$ as $t \rightarrow \infty $,we know that $\sum_{j=1}^{n+m}\frac{\partial V_{ij}}{\partial x_i}+\sum_{j=1}^{n+m} a_{ij}(x_i-x_j)\rightarrow0$ as $t \rightarrow \infty$. According to Lemma 1,$-\mathcal {T}^{-1} \mathcal {T}_d \otimes I_p x_l \in {\rm co}\{x_j,\nu_j \in L\}$ with $x_i$ $=$ $[x_{n+1}^{\rm T}$,$x_{n+2}^{\rm T}$,$\cdots$,$x_{n+m}^{\rm T}]^{\rm T} \in {\bf R}^{pm}$,we know that $\frac{1}{\sum_{j=1}^{n+m}a_{ij}} \sum_{j=1}^{n+m}a_{ij} x_j$ is in the convex hull $ {\rm co}\{x_j,\nu_j \in L\}$,and $\lambda_{\min}(\mathcal {T})>0$ when connectivity maintenance Assumption 1 holds. Thus, \begin{align*} \varphi_i \leq&\ \left\|x_i-\frac{1}{\sum\limits_{j=1}^{n+m}a_{ij}} \sum_{j=1}^{n+m}a_{ij} x_j \right\| \leq\\ &\ \frac{1}{\lambda_{\min}(\mathcal {T})} \left\| \sum_{j=1}^{n+m}a_{ij}(x_i-x_j) \right\| =\\ &\ \frac{1}{\lambda_{\min}(\mathcal {T})} \left\| \frac{\partial V_{ij}}{\partial x_i} \right\|\leq\\ &\ \frac{1}{\lambda_{\min}(\mathcal {T})}\sum_{j=1}^{n+m} \left\|\frac{\partial V_{ij}}{\partial x_i}\right\|. \end{align*} It can then be shown that $$\varphi_i=\inf\left\{\|x_i-y\|:y\in {\rm co}\{x_j,\nu_j \in L\}\right\}$$ is bounded and $\varphi=\sum_{i=1}^{n}\varphi_i$ is ultimately bounded.
B. SimulationIn this section,numerical simulation results are given to validate the theoretical results. Let $\dot{x}_j=[\begin{array}{cc} 0.32 & 0 \\ \end{array}]^{\rm T}$ and $\ddot{x}_j$ $=$ $[\begin{array}{cc} 0 & 0 \\ \end{array}]^{\rm T}$ all the time. Let $r=20$,$d_1=1$,$k=1.0$, $\delta$ $=$ $1.0$.
We first consider the case that there are two leaders and only one follower in the group. The initial state of the agents are given as $x_1(0)=[\begin{array}{cc} 0 & 2.5 \\ \end{array}]^{\rm T}$,$\dot{x}_1(0)=[\begin{array}{cc} 0.1 & 0 \\ \end{array}]^{\rm T}$,$x_2(0)=[\begin{array}{cc} 4 & 1 \\ \end{array}]^{\rm T}$,$x_3(0)=[\begin{array}{cc} 4 & -1 \\ \end{array}]^{\rm T}$. The adjacency matrix is \[\mathcal{A}=\left[\begin{array}{ccc} 0 & 1 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right].\]
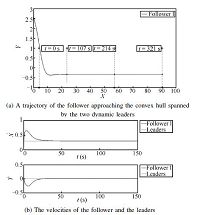
Fig. 2 shows the trajectory of the follower moving to the center of the two leaders and the velocity of the follower converges to that of the dynamic leaders. In the figure,the little ``square" and the ``plus" sign represent respectively the initial and final positions of each robot. It can be seen that under control law (2),the follower is capable of recognizing and tracking the leaders and it approaches the containment of the leaders while maintaining a minimum distance among agents.
We next consider the case of one follower and three leaders. The initial state of the agents are given as $x_1(0)=[\begin{array}{cc} -4 & 4 \\ \end{array}]^{\rm T}$,$\dot{x}_1(0)=[\begin{array}{cc} -0.1 & 0.1 \\ \end{array}]^{\rm T}$,$x_2(0)=[\begin{array}{cc} 4 & 0 \\ \end{array}]^{\rm T}$,$x_3(0)$ $=$ $[\begin{array}{cc} 0 & -3 \\ \end{array}]^{\rm T}$,$x_4(0)=[\begin{array}{cc} 0 & 3 \\ \end{array}]^{\rm T}$. The adjacency matrix is \[\mathcal{A}=\left[\begin{array}{cccc} 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} \right].\]
|
Download:
|
| Fig. 2.A trajectory of the follower approaching the convex hull spanned by the two dynamic leaders ($(X,Y)$ are the coordinates of the agent$'$s position.). | |
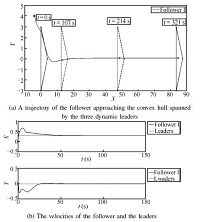
Fig. 3(a) shows the trajectory of the follower approaching the convex hull spanned by the three dynamic leaders. Fig. 3(b) shows that the velocity of the follower approaches that of the leaders.
Finally,the case that two followers approach the convex hull formed by three dynamic leaders is simulated. The initial state of the agents are given as $x_1(0)=[\begin{array}{cc} -5 & 10 \\ \end{array}]^{\rm T}$,$\dot{x}_1(0)$ $=$ $[\begin{array}{cc} 0.1 & 0.1 \end{array}]^{\rm T}$,$x_2(0)=[\begin{array}{cc} 5 & -10 \end{array}]^{\rm T}$,$\dot{x}_2(0)=[\begin{array}{cc} -0.3 & 0 \end{array}]^{\rm T}$,$x_3(0)$ $=$ $[\begin{array}{cc} 8 & 0 \end{array}]^{\rm T}$,$x_4(0)$ $=$ $[\begin{array}{cc} 0 & -6 \end{array}]^{\rm T}$,$x_5(0)$ $=$ $[\begin{array}{cc} 0 & 6 \end{array}]^{\rm T}$. The adjacency matrix is \[\mathcal{A}=\left[\begin{array}{ccccc} 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right].\]
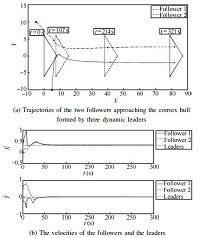
Fig. 4 shows the starting positions and the ending positions of the two followers as well as the convex hull spanned by the three leaders. It can be seen that the trajectories of the two followers approach the dynamic leaders and one follower moves into the convex hull of the leaders at $t=107$s. At $t=214$s,both followers are within the convex hull formed by the three leaders and start to move along with the leaders at the same velocity.
|
Download:
|
| Fig. 3.A trajectory of the follower approaching the convex hull spanned by the three dynamic leaders ($(X,Y)$ are the coordinates of the agent$'$s position.). | |
|
Download:
|
| Fig. 4.Trajectories of the two followers approaching the convex hull formed by the three dynamic leaders ($(X,Y)$ are the coordinates of the agent$'$s position.). | |
In the experiments,five wheeled mobile robots are divided into two groups. Three of them are designated as the leaders and two as the followers.
The adjacency matrix $\mathcal{A}$ associated with the communication graph can be calculated from the initial states of the followers and the leaders. The control parameters are chosen as the sensing radius $r=45$ cm,the minimum safety distance $d_1=2$cm,$k=1.0$ and $\delta=1.0$. The velocities of the leaders are set to be $v_j=[3.2 \quad 0]^{\rm T}$cm/s,$\nu_j \in L$.
We first consider the case that there are two leaders and only one follower in the multi-agent system. Fig. 5 shows that the trajectory of the follower approaching the center of two dynamic leaders. It can be seen that the follower is able to recognize and track the leaders,then enters and stays within the convex hull formed by the two leaders while maintaining a minimum distance from other agents and moving at the same final velocity as the leaders.

|
Download:
|
| Fig. 5.A trajectory of the follower tracking two dynamic leaders. | |
The case of three leaders with one follower is then experimented on and the trajectory of a follower approaching the convex hull spanned by the three dynamic leaders is shown in Fig. 6. It can be seen that the follower is first driven to the center of the nearest two leaders,and then approaches the convex hull spanned by the three leaders while avoiding collision and finally ensuring velocity matching.
Finally,the case that two followers tracking three leaders is experimented. Fig. 7 shows the starting positions and the ending positions of the two followers as well as the convex hull spanned by the three leaders. It can be seen that the trajectories of the two followers approach the containment of the three leaders while ensuring group dispersion and velocity matching.

|
Download:
|
| Fig. 6.A trajectory of the one follower approaching the convex hull spanned by the three dynamic leaders. | |

|
Download:
|
| Fig. 7.Trajectories of the two followers approaching the convex hull formed by the three dynamic leaders. | |
In this paper,we studied the containment and group dispersion control for a multi-robot system in the presence of dynamic leaders. A distributed control algorithm was developed to drive the follower robots to converge to the dynamic leader robots with containment and group dispersion behaviors. Both simulation results and experimental results on the multi-robot platform were presented to validate the theoretical results. Real world constraints,including actuator saturation,will be addressed in the future work.
| [1] | Ren W, Beard R W, Atkins E W. Information consensus in multivehicle cooperative controlcollective group behavior through local interaction. IEEE Control Systems Magazine, 2007, 27(2):71-82 |
| [2] | Ren W. Consensus tracking under directed interaction topologies:algorithms and experiments. In:Proceedings of the 2008 American Control Conference. Seattle, WA, USA:IEEE, 2008. 742-747 |
| [3] | Peng K, Yang Y P. Leader-following consensus problem with a varyingvelocity leader and time-varying delays. Physica A:Statistical Mechanics and its Applications, 2008, 388(2):193-208 |
| [4] | Cao Y C, RenW, Li Y. Distributed discrete-time coordinated tracking with a time-varying reference state and limited communication. Automatica, 2009, 45(5):1299-1305 |
| [5] | Fang L, Antsaklis P J. Information consensus of asynchronous discretetime multi-agent systems. In:Proceedings of the 2005 American Control Conference. Portland, OR, USA:IEEE, 2005. 1883-1888 |
| [6] | Ren W, Chao H Y, Bourgeous W, Sorensen N. Experimental validation of consensus algorithms for multivehicle cooperative control. IEEE Transactions on Control Systems Technology, 2008, 16(5):745-752 |
| [7] | Jadbabaie A, Lin J, Morse A. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Transactions on Automatic Control, 2003, 48(6):988-1001 |
| [8] | Jin Z, Murray R. Consensus controllability for coordinated multiple vehicle control. In:Proceedings of the 6th International Conference on Cooperative Control and Optimization. Gainesville, FL, USA, 2006 |
| [9] | Moore K, Lucarelli D. Decentralized adaptive scheduling using consensus variables. International Journal of Robust and Nonlinear Control, 2007, 17(10-11):921-940 |
| [10] | Cao Y C, Ren W. Containment control with multiple stationary or dynamic leaders under a directed interaction graph. In:Proceedings of the 2009 Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference. Shanghai, China:IEEE, 2009. 3014-3019 |
| [11] | Cao Y C, Stuart D, Ren W, Meng Z Y. Distributed containment control for multiple autonomous vehicles with double-integrator dynamics:algorithms and experiments. IEEE Transactions on Control Systems Technology, 2011, 19(4):929-938 |
| [12] | Ji M, Ferrari-Trecate G, Egerstedt M, Buffa A. Containment control in mobile networks. IEEE Transactions on Automatic Control, 2008, 53(8):1972-1975 |
| [13] | Dimarogonas D, Egerstedt M, Kyriakopoulos K. A leader-based containment control strategy for multiple unicycles. In:Proceedings of the 45th IEEE Conference on Decision and Control. San Diego, CA, USA:IEEE, 2006. 5968-5973 |
| [14] | Zhang H J, Meng Z Y, Lin Z L. Experimental verification of a multirobot distributed control algorithm with containment and group dispersion behaviors. In:Proceedings of the 31th Chinese Control Conference. Hefei, China:IEEE, 2012. 6159-6164 |
| [15] | Lou Y, Hong Y. Target containment control of multi-agent systems with random switching interconnection topologies, Automatica, 2012, 48(5):879-885 |
| [16] | Shi G D, Hong Y G, Johansson K H. Connectivity and set tracking of multi-agent systems guided by multiple moving leaders. IEEE Transactions on Automatic Control, 2011, 57(3):663-676 |
| [17] | Shi G, Hong Y. Global target aggregation and state agreement of nonlinear multi-agent systems with switching topologies. Automatica, 2009, 45(5):1165-1175 |
| [18] | Cao Y C, Ren W, Sorensen N, Ballard L, Reiter A, Kennedy J. Experiments in consensus-based distributed cooperative control of multiple mobile robots. In:Proceedings of the 2007 International Conference on Mechatronics and Automation. Harbin, China:IEEE, 2007. 2819-2824 |
| [19] | Cook J, Hu G Q. Experimental verification and algorithm of a multi-robot cooperative control method. In:Proceedings of the 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM). Montreal, ON:IEEE, 2010. 109-114 |
| [20] | Meng Z Y, Ren W, You Z. Distributed finite-time attitude containment control for multiple rigid bodies. Automatica, 2010, 42(12):2092-2099 |
 2014, Vol.1
2014, Vol.1 


