2. EXQUISITUS, Centre for ECity, School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore 639798, Singapore;
3. Ministry of Science and Technology, Bangkok 10400, Thailand;
4. Massachusetts Institute of Technology, Cambridge MA 02139, USA
Traffic congestion causes significant efficiency losses,wasteful energy consumption and excessive air pollution. This problem arises in many urban areas because of the continual growth in motorization and the difficulties in increasing road capacity due to space limitations and budget constraints. As a result,traffic management that aims at maximizing the efficiency and effectiveness of road networks without increasing road capacity becomes increasingly crucial. A case study on the traffic system in California shows that transportation pricing such as congestion pricing,parking pricing,fuel tax pricing,vehicle miles of travel fees and emissions fees can better manage the transportation system to a great extent[1]. As another example,the electronic road pricing (ERP) system in Singapore charges motorists when they use certain roads during the peak hours in order to maintain an optimal speed range for both expressways and arterial roads[2, 3]. The road pricing system is typically implemented for two main objectives. First,it is designed to affect the route-choice behaviors. For example,the charges on expressways motivate motorists to use alternative,less congested,arterial roads even though it comes at the cost of extra travel time. Second,road pricing is enforced on many of the roads in the city area in order to refrain the motorists from using those roads during the peak hours as no alternative route with cheaper rate is possible. Hence,a significant portion of the motorists will either turn to public transportation or rearrange their schedules to avoid entering the city during the peak hours. A comprehensive review of the design and evaluation of road pricing schemes can be found,for example,in [4, 5]. Note that each motorist usually selects his or her trip routing and trip timing behavior by myopically optimize his or her own utility as a function of road price. At the same time,each motorist may collectively communicate with his or her friends and neighbors on traffic situation from time to time. Therefore,game theory and consensus theory provide a natural framework for road pricing design.
Game theory deals with strategic interactions among multiple players,where each player tries to maximize his or her own utility[6, 7]. It is applied in a broad array of areas including economics,social science,engineering,etc. For any non-trivial game,the utility of each player depends on choices or actions of at least one other player and generally of all the players. Nash equilibrium,a fundamental concept in the realm of noncooperative game theory,is defined as the action profile of all players where none of the players can improve his or her utility by a unilateral move. It essentially characterizes the user optimal situation,where the utility function of every myopic player reaches a local optimum.
In this paper,we consider repeated games where in each stage,the players are allowed to choose their actions based on the available information. Generally,players need to learn the underlying structure of the game by observing the decisions made by other players,especially when players have only limited or even no knowledge of their opponents$'$ utilities. Fictitious play and its variants are classical learning processes studied extensively in the literature. In a standard fictitious play,each player computes the empirical frequencies of the observed decisions and assumes that all other players make decisions independently according to those empirical frequencies[8]. Several counterexamples show that fictitious play needs not converge[9, 10]. However,it has been proved by using a Lyapunov stability approach that convergence is possible under some non-singularity conditions if we have either a zero-sum game,an identical interest game,or a two-player/two-move game[11]. It is also known that the empirical frequencies generated by fictitious play of a potential game converge to a mixed strategy Nash equilibrium[12]. One obvious shortcoming of fictitious play is that when the number of players is large,it is computationally infeasible to obtain the best response for each player,since the best response of a player depends on a mapping over a joint action space of other players. See Section II for more details.
As a variant of fictitious play,a joint strategy fictitious play (JSFP) alleviates the informational and computational burden of standard fictitious play by introducing a utility updating process for each player[8, 13]. Different from standard fictitious play,in the JSFP,each player assumes that all other players make decisions jointly according to their joint empirical frequencies. Also see Section II for more details. In the case of the JSFP with inertia,the convergence to a pure strategy Nash equilibrium is established for all generalized ordinal potential games[13].
Note that in the realm of noncooperative game theory[7],no cooperation is allowed among the players. In contrast,the selection of actions is done collectively with full trust in the realm of cooperative game theory,e.g.,consensus. For a group of agents, consensus means to reach an agreement on a quantity of interest which depends on the state of every agent[14]. There has been a lot of research on discrete-time consensus. Consensus conditions and convergence speed for discrete-time multi-agent networks with fixed topology were explored in [14]. Necessary and sufficient conditions on consensus over random networks were provided in [15, 16]. In [17, 18],discrete-time average-consensus under switching network topologies was analyzed. Further,the work in [19, 20] gave consensus convergence rates in dynamically changing environments.
In [21],a continuous-time distributed protocol was proposed to estimate the number of active players at each stage. Under this structure,a best response path algorithm was established for a finite noncooperative game. Such an algorithm generated a sequence of joint decisions obtained by a single player$'$s unilateral improvement from previous stage which eventually converged to a Nash equilibrium. Furthermore,a discrete-time consensus protocol under a fixed network topology was designed in [22] to estimate the percentage of active players and allow the best response strategy to converge to a unique Pareto optimal Nash equilibrium. However,these results can only be applied to binary strategies.
The contributions of this paper can be summarized as follows. First of all,we present a new variant of fictitious play called average strategy fictitious play (ASFP) and prove its convergence for a congestion game under some reasonable assumptions. Note that the computational burden of each player in the JSFP mainly comes from the utility updating process and increases with the number of possible actions. The ASFP proposed in this paper reduces the computational burden of the JSFP by getting rid of the utility updating process. In the ASFP,each player only obtains a weighted running average of all other players$'$ actions and assumes that the total number of other players choosing one action is equal to the weighted running average corresponding to this action. In addition, we formulate a multiple choices congestion game under random networks,and a consensus protocol is implemented to estimate the number of players selecting each resource without the system surpervisor$'$s broadcasting. The convergence property of underlying congestion game with or without broadcasting is established.
Secondly,we apply the results to the road pricing problem. The road pricing system is typically implemented for affecting motorists$'$ route choices[23, 24] and trip timing choices[3, 28]. We formulate the trip timing problem as a congestion game. Congestion game as a special case of potential game was first introduced in [26],where a collection of homogeneous agents had to choose from a finite set of alternatives and the payoff of a player depended on the number of players choosing each alternative. Different from [26],players$'$ utilities are heterogeneous in this paper.
Preliminary results of this paper were reported in [27, 28]. The remainder of the paper is organized as follows. Section II summarizes a series of notations and some pertinent work,and also provides the model setup of this paper. Sections II and III establish the theoretical framework of this paper. The structure and the convergence property of the ASFP with broadcasting is given in Section II. In Section III,a consensus protocol is introduced and the convergence to a pure Nash equilibrium is also proved. In Section IV,the results are applied to the design of road pricing scheme,and simulations based on the real traffic data in Singapore are also included. Finally,Section V concludes the paper and discusses the future work.
II. NOTATIONS, RELATED WORK, AND MODEL SETUPConsider a repeated finite $N$-player game with the set of players ${\bf N}=\{1,2,\cdots,N\}$ over consecutive stages $t=0,1$,2, $\cdots$. For any $i\in {\bf N}$,$-i$ denotes the complementary set ${\bf N}\backslash\{i\}$. The action of player $i$ at stage $t$ is denoted by $x_i(t)$ $\in$ $X_i$,and $X_i$ is the action set. For the rest of the paper,argument $t$ may be omitted when no confusion is caused. Let $x$ $=$ $(x_i$,$x_{-i})$ represent the action profile of all the players. Here $x_{-i}$ is the profile of player actions other than player $i$,and similar notation will be used for other vectors as well. The utility received by player $i$ is denoted by $U_i(x_i,x_{-i})$ or simply $U_i(x)$.
The definition of potential game is given as follows[12]. Note that if a game admits a potential function,then all players tend to jointly optimize the potential function.
${\bf Definition 1.}$ A finite $N$-player game with utility functions
$U_1(x),U_2(x),\cdots,U_N(x)$ is called a potential game if there
exists a potential function $\Phi(x)$ such that for every $i$ $\in$
${\bf N}$,
\begin{align}
U_i(x_i^1,x_{-i})-U_i(x_i^2,x_{-i})=\Phi(x_i^1,x_{-i})-\Phi(x_i^2,x_{-i}),
\end{align}
(1)
An $N$-tuple of action variable $x^*$ constitutes a (pure strategy)
Nash equilibrium[7],if for all possible $i\in{\bf N}$,$x_i$
$\in$ $X_i$,
\begin{align}
U_i(x_i^*,x_{-i}^*)\geq
U_i(x_i,x_{-i}^*).
\end{align}
(2)
The standard fictitious play is an iterative learning process
incorporating the empirical frequencies of opponents$'$ actions
without assuming any information of other players$'$
utilities[8]. Denote
$f_i^{\hat{x}_i}(t)=\frac{1}{t}\sum_{s=0}^{t-1}{I}\{x_i(s)=\hat{x}_i\}$
as the empirical frequency of player $i$ choosing action
$\hat{x}_i\in X_i$ up to stage $t-1$. Here ${I}\{\cdot\}$ is the
indicator function. Every player assumes that other players make
decisions randomly and independently according to those empirical
frequencies,then the expected utility for player $i$ choosing
$\hat{x}_i\in X_i$ is
\begin{align}
\bar{U}_i(\hat{x}_i,f_{-i}(t))=\sum_{\hat{x}_{-i}\in
X_{-i}}U_i(\hat{x}_i,\hat{x}_{-i})\prod_{j\in{-i}}f_j^{\hat{x}_j}(t).
\end{align}
(3)
In the JSFP,the empirical frequencies of the joint actions of other
players,defined as
$g_{-i}^{\hat{x}_{-i}}(t)=\frac{1}{t}\sum_{s=0}^{t-1}{I}\{x_{-i}(s)=\hat{x}_{-i}\}$,
are tracked by player $i$. Every player assumes that other players
make decisions randomly and jointly according to the above
empirical frequencies. The expected utility for player $i$
choosing $\hat{x}_i\in X_i$ becomes
\begin{align}
\bar{U}_i(\hat{x}_i,g_{-i}(t))=\sum_{\hat{x}_{-i}\in
X_{-i}}U_i(\hat{x}_i,\hat{x}_{-i})g_{-i}^{\hat{x}_{-i}}.
\end{align}
(4)
\begin{align}
&\bar{U}_i(\hat{x}_i,g_{-i}(t+1))= \nonumber \\
&\qquad
\frac{t}{t+1}\bar{U}_i(\hat{x}_i,g_{-i}(t))+\frac{1}{t+1}U_i(\hat{x}_i,x_{-i}(t)).
\end{align}
(5)
In this paper,we consider a congestion game where the action of
player $i$ at stage $t$ is chosen from a finite collection of
common resources ${\bf R}=\{r_1,r_2,\cdots,r_M\}$. For the ease of
the presentation,we limit our attention to a single choice case,
i.e.,the cardinality of $x_i(t)\in{\bf R}$ is $1$. However,the
results presented here can be further extended to a multiple
choices case. It is assumed that the utility received by player
$i$ can be divided into two parts as
\begin{align}
U_i(x_i,x_{-i})=V_{1i}(x_i)+V_2(n_{x_i}(x)),
\end{align}
(6)
\begin{align}
n_{x_i}(x)=\sum_{j=1}^N{I}\{x_j=x_i\}
\end{align}
(7)
In this section,a system supervisor is assumed which broadcasts information about the overall system to every player at each stage. We introduce the ASFP to further reduce the computational burden of the JSFP by getting rid of the utility updating process (5), and then analyze its convergence property.
A.ASFP
The procedure of the ASFP is described as follows. At the initial
stage $t=0$,every player picks up an action arbitrarily from
${\bf R}$. Then at any stage $t\geq1$,the system supervisor
records $n_{r_l}(x(t-1))$ for all $l=1,2,\cdots,M$,and computes
its weighted running average recursively as
\begin{align}
&\bar{n}_{r_l}(0)=n_{r_l}(x(0)),\nonumber\\
&\bar{n}_{r_l}(t)=(1-\lambda)\bar{n}_{r_l}(t-1)+\lambda
n_{r_l}(x(t-1)),
\end{align}
(8)
\begin{align}
\bar{n}_{r_l}^{-i}(t)=\bar{n}_{r_l}(t)-w_{r_l}^i(t),
\end{align}
(9)
\begin{align}
\bar{U}_i(\hat{x}_i,\bar{n}^{-i}(t))=V_{1i}(\hat{x}_i)+V_2(\bar{n}_{\hat{x}_i}^{-i}(t)+1),
\end{align}
(10)
\begin{align}
&\mathrm{BR}_i(\bar{n}^{-i}(t))= \nonumber \\
&\qquad \{\tilde{x}_i\in {\bf
R}|\bar{U}_i(\tilde{x}_i,\bar{n}^{-i}(t))=\max_{x_i\in {\bf
R}}\bar{U}_i(x_i,\bar{n}^{-i}(t))\}.
\end{align}
(11)
${\bf Remark 1.}$ Different from the JSFP,the utility updating process (5) is avoided in the ASFP,and thus the burden for information processing of each player is reduced especially when the number of resources to be chosen from is large. Next,given the best response set $\mathrm{BR}_i(\bar{n}^{-i}(t))$ for every player $i$ at every stage $t\geq1$,we will study convergence of the ASFP.
B.Convergence AnalysisThe convergence property of the ASFP is established via two steps. First,we will prove the existence of a set of Nash equilibria for the congestion game. After that,we will show that players$'$ actions generated by the ASFP with some kind of inertia converge to one of Nash equilibrias almost surely.
The following proposition shows that the congestion game defined above is a potential game; thus,it inherits the desirable property of potential game regarding the existence of a pure strategy Nash equilibrium.
${\bf Proposition 1.}$ A congestion game with utility functions
given in (6) is a potential game with the potential function
\begin{align}
\Phi(x)=\sum_{j=1}^N
V_{1j}(x_j)+\sum_{l=1}^{M}\sum_{k=1}^{n_{r_l}(x)}V_2(k),
\end{align}
(12)
${\bf Proof.}$ For the case: $x_i^1=x_i^2$,condition (1) obviously holds. For the case: $x_i^1\neq x_i^2$,we have \begin{align*} &\Phi(x_i^1,x_{-i})-\Phi(x_i^2,x_{-i})=\\ &\qquad \sum_{l=1}^{M}\sum_{k=1}^{n_{r_l}(x_i^1,x_{-i})}V_2(k)-\sum_{l=1}^{M}\sum_{k=1}^{n_{r_l}(x_i^2,x_{-i})}V_2(k) +\\ &\qquad V_{1i}(x_i^1)-V_{1i}(x_i^2)=\\ &\qquad V_2(n_{x_i^1}(x_i^1,x_{-i}))-V_2(n_{x_i^2}(x_i^2,x_{-i})) +\\ &\qquad V_{1i}(x_i^1)-V_{1i}(x_i^2)=\\ &\qquad U_i(x_i^1,x_{-i})-U_i(x_i^2,x_{-i}), \end{align*} i.e.,condition (1) is satisfied. The proof is completed since every potential game has at least one pure strategy Nash equilibrium[12].
For the simplicity of the analysis,we make the following assumption on the utility induced by congestion. Its validity will be further justified in Section V on transportation modeling.
${\bf Assumption 1.}$ The utility part induced by congestion in (6)
is linear with respect to the number of players selecting the same
resource,i.e.,
\begin{align}
V_2(n_{x_i}(x))=an_{x_i}(x)+b,
\end{align}
(13)
Following the idea in [13, 29],some sort of inertia,which plays an important role in the convergence analysis,is introduced in players$'$ decision making process. In the presence of inertia, player $i\in{\bf N}$ stays with the previous action,i.e.,$x_i(t)$ $=$ $x_i(t-1)$,if there is no opportunity for utility improvement, i.e.,$x_i(t-1)\in\mathrm{BR}_i(\bar{n}^{-i}(t))$; otherwise,he or she chooses an action from the set $\mathrm{BR}_i(\bar{n}^{-i}(t))$ with probability $\xi_i(t)$ and still stays with the previous action with probability $1-\xi_i(t)$. The absorption property of Nash equilibria in the ASFP with inertia is shown in the following lemma.
${\bf Lemma 1.}$ Consider a congestion game with utility functions given in (6). Under Assumption 1,if the action profile $x(t)$ of all players generated by the ASFP with inertia is a pure strategy Nash equilibrium at stage $t$,and $x_i(t)$ $\in$ $\mathrm{BR}_i(\bar{n}^{-i}(t))$ for every $i\in{\bf N}$,then $x(t+\tau)=x(t)$ for any positive integer $\tau$.
${\bf Proof.}$ First note that
\begin{align}
n_{\hat{x}_i}(\hat{x}_i,x_{-i}(t))=n_{\hat{x}_i}(x(t))-\mathrm{I}\{x_i(t)=\hat{x}_i\}+1.
\end{align}
(14)
\begin{align}
\bar{n}_{r_l}^{-i}(0)=&\ n_{r_l}(x(0))-\mathrm{I}\{x_i(0)=r_l\},\nonumber \\
\bar{n}_{r_l}^{-i}(t)=&\ (1-\lambda)\bar{n}_{r_l}^{-i}(t-1) + \nonumber \\
&\ \lambda(n_{r_l}(x(t-1))-\mathrm{I}\{x_i(t-1)=r_l\}).
\end{align}
(15)
\begin{align}
&\bar{U}_i(\hat{x}_i,\bar{n}^{-i}(t+1))=\nonumber\\
&\quad~ V_{1i}(\hat{x}_i)+V_2(\bar{n}_{\hat{x}_i}^{-i}(t+1)+1)=\nonumber\\
&\quad~a\{(1-\lambda)\bar{n}_{r_l}^{-i}(t)+\lambda(n_{r_l}(x(t))-\mathrm{I}\{x_i(t)=r_l\})\} +\nonumber\\
&\quad~a+b+V_{1i}(\hat{x}_i)=\nonumber\\
&\quad~(1-\lambda)\bar{U}_i(\hat{x}_i,\bar{n}^{-i}(t))+\lambda
U_i(\hat{x}_i,x_{-i}(t)).
\end{align}
(16)
\begin{align}
\bar{U}_i(x_i(t),\bar{n}^{-i}(t))\geq\bar{U}_i(\hat{x}_i,\bar{n}^{-i}(t)).
\end{align}
(17)
\begin{align}
U_i(x_i(t),x_{-i}(t))\geq U_i(\hat{x}_i,x_{-i}(t)).
\end{align}
(18)
\begin{align}
\bar{U}_i(x_i(t),\bar{n}^{-i}(t+1))\geq\bar{U}_i(\hat{x}_i,\bar{n}^{-i}(t+1)),
\end{align}
(19)
Two technical assumptions are essential to convergence analysis of the ASFP: one on players$'$ willingness to optimize the predicted utility,and the other on players$'$ difference between any two distinct strategies.
${\bf Assumption 2.}$ For every player $i\in{\bf N}$ and for every
stage $t\geq1$,there exist constants $\delta_1$ and $\delta_2$
such that
\begin{align}
0<\delta_1\leq\xi_i(t)\leq\delta_2<1.
\end{align}
(20)
${\bf Assumption 3.}$ For every player $i\in{\bf N}$,
\begin{align}
U_i(x_i^1,x_{-i})\neq U_i(x_i^2,x_{-i}),
\end{align}
(21)
As the main result of this paper,the convergence property of the ASFP is provided in the next theorem.
${\bf Theorem 1.}$ Consider a congestion game with utility functions given in (6) and broadcasting. Under Assumptions 1 $\sim$ 3,the action profile of all players generated by the ASFP with inertia is convergent to a pure strategy Nash equilibrium almost surely.
${\bf Proof.}$ According to (16),if $x(t)$ is repeated $T$ times,
i.e.,$x(t)=x(t+1)=\cdots=x(t+T-1)$,then
\begin{align*}
\bar{U}_i(\hat{x}_i,\bar{n}^{-i}(t+T-1))=&\ (1-\lambda)^{T-1}\bar{U}_i(\hat{x}_i,\bar{n}^{-i}(t)) +\\
&\ (1-(1-\lambda)^{T-1})U_i(\hat{x}_i,x_{-i}(t)).
\end{align*}
For $\lambda\in(0,1]$,there exists a sufficiently large $T$
independent of $t$ such that
$\mathrm{BR}_i(\bar{n}^{-i}(t+T-1))=\mathrm{BR}_i(x_{-i}(t))$,where
$\mathrm{BR}_i(x_{-i}(t))$ is defined as the best response of player
$i$ with respect to the action profile of other players $x_{-i}(t)$,
i.e.,
\begin{align}
&\mathrm{BR}_i(x_{-i}(t))= \nonumber \\
&\qquad ~\{\tilde{x}_i\in {\bf
R}|U_i(\tilde{x}_i,x_{-i}(t))=\max_{x_i\in {\bf
R}}U_i(x_i,x_{-i}(t))\}.
\end{align}
(22)
\begin{align}
\Phi(x(t))<\Phi(x(t+T))<\dots<\Phi(x(t+KT)).
\end{align}
(23)
Note that the cardinality of the decision space of all players is
$M^N$,which is finite. In addition,there always exists at least
one pure strategy Nash equilibrium for the underlying congestion
game. Therefore,there exists a finite $K
${\bf Remark 2.}$ As we can see from the proof of Theorem 1,if
there are multiple Nash equilibria for the underlying game,then
the action profile may converge to a pure strategy Nash
equilibrium corresponding to only a local maximum point of the
potential function. Note that this kind of phenomenon also
motivates the research work on inefficiency of
equilibria[30],which can be one of our future directions.
In this section,we turn to consider the case without the system
supervisor. In this situation,no information on the overall
system is collected or broadcasted. A discrete-time consensus
protocol is formulated for individual players to estimate the
percentage/number of players choosing each resource,and then the
convergence property of players$'$ action profile is also
analyzed.
Note that the main purpose of multi-agent consensus for individual
player is to estimate $n_{r_l}(x(t))$ defined in (7),or
equivalently ${n_{r_l}(x(t))}/{N}$,by using only local information
obtained from neighboring players. The consensus process is repeated
during every stage,and thus we take one stage $t$ as an example in
this section without loss of generality.
Suppose that the whole time interval of stage $t$ is further divided
into several short time intervals $k=0,1,2,\cdots,K$. At each short
time interval $k$,player $i$ randomly exchanges information with
$N_i(k)$,a subset of its whole neighbor set ${\bf N}_i$. Let
$\bar{\cal G}_N$ denote the set of all possible undirected graphs
consisting of the node set ${\bf N}$ and an edge set ${\cal
E}\subset{\bf N}\times{\bf N}$,in which the necessary conditions
for non-oriented pair $(i,j)$ $\in$ ${\cal E}$,$i\neq j$ are
$i\in{\bf N}_j$ and $j\in{\bf N}_i$. As stated above,at each short
time interval $k$,the network is chosen from $\bar{\cal G}_N$
randomly,independent of other short time intervals. We denote the
graph at $k$ as ${\cal G}_N(k)=\{{\bf N},{\cal E}(k)\}\in\bar{\cal
G}_N$ and the corresponding neighbor set of player $i$ as
$N_i(k)=\{j:$ $(i,j)$ $\in$ ${\cal E}(k)\}$ $\cup$ $\{i\}$. Let
$L(k)$ be the symmetrical Laplacian matrix associated with ${\cal
G}_N(k)$ and use $L_{ij}(k)$ to denote the $i,j$ entry of $L(k)$.
Note that ${\cal G}_N(k)$ may not be connected and some agents may
be isolated as they may leave the system randomly. For an isolated
agent $i$ at $k$,its neighbor set is $N_i(k)=\{i\}$. In addition,
the union of the undirected graphs ${\cal G}_N(k),k=0,1,\cdots,K$,
is said to be jointly connected,if there exists an undirected path
between each pair of nodes[20].
Write $s_i(t)=[s_{i1}(t)\ s_{i2}(t)\dots s_{iM}(t)]'$,where
$s_{ij}(t)=1$ if $x_i(t)=r_j$,otherwise $s_{ij}(t)=0$. Note that
$s_i(t)$ is available to player $i$ at the beginning of stage $t$.
For the single choice case studied in this paper,we have
$\sum_{j=1}^Ms_{ij}(t)=1$. Motivated by the protocol introduced in
[21] for the case of binary strategies,a linear protocol is given
by
By considering the $l$-th element of $y_i(k)N$ as an estimate of
$n_{r_l}(x(t))$,the ASFP presented in Section III-A can still be
applied.
Based on the consensus theory[14, 20],we can easily obtain
the following results.
${\bf Lemma 2.}$ The protocol described by (24) satisfies that for
$k=0,1,2,\cdots,K$,
${\bf Lemma 3.}$ If there exists a $K$ such that the union of the
undirected graphs ${\cal G}_N(k)$,$k=0,1,\cdots,K$,is jointly
connected,then the protocol described by (24) achieves average
consensus exponentially fast,which indicates that for any
$\epsilon$ $>$ $0$,there exists a finite integer $K\geq1$ such that
Based on the above two lemmas and following the similar line of
proof as in Theorem 1,we can derive the result below.
${\bf Proposition 2.}$ Suppose that there exists a $K$ such that for
each stage $t$,the union of the undirected graphs ${\cal G}_N(k)$,
$k$ $=$ $0,1,\cdots,K$,is jointly connected,and the number of
short time intervals $K+1$ is sufficiently large. Consider a
congestion game with utility functions given in (6) and without
broadcasting. Under Assumptions 1 $\sim$ 3,the action profile of
all players generated by the ASFP with inertia and the consensus
protocol in (4) is convergent to a pure strategy Nash equilibrium
almost surely.
Suppose that a group of people with one origin and one destination
are planning to travel during a given period (e.g.,
7: 30 am $\sim$ 9: 30 am) on a daily basis. There are $M_1$
parallel routes connecting the origin and the destination,and the
given time period is divided into $M_2$ time intervals. In this
case,the common resources contain both trip routing and trip timing
choices with $M=M_1M_2$. In the following text,we focus on
motorists$'$ trip timing behavior by setting $M_1=1$.
For the problem of trip timing,a collection of time intervals is
considered as the set of resources to be chosen by every road user.
Without road price,each driver decides his or her departure time by
taking the average travel speed and his or her own preferred
departure time into account. Suppose that $n_{r_i}(x)$ is the number
of vehicles on the road choosing departure time interval $r_i$ and
the length of the road is $L_r$. A common assumption in the area of
transportation theory is that the average travel speed is a linear
function of traffic density,i.e.,$n_{r_i}(x)/L_r$; see,e.g.,
[31, 32]. In this case,we set the utility parts $V_{1i},V_2$ in
(6) as
For the case with broadcasting,the road manager (i.e.,the system
supervisor) monitors the traffic flows in the traffic system,and
thus the weighted running average defined in (8) can be computed
by the road manager. The weighted running average actually
describes the crowdedness of the road during each time interval
based on the historical traffic situation. Suppose that the road
manager broadcasts (8) to every driver. Then,the above trip
timing problem fits within the congestion game formulated in
Sections 1 and 2. Moreover,if every driver generates his or her
action based on the ASFP with inertia,then the convergence of the
action profile of all drivers is ensured under the conditions of
Theorem 1.
For the case without broadcasting,individual driver exchanges
information on traffic situation with his or her friends and
neighbors randomly in order to estimate the number of drivers
selecting each departure time interval. Then,the consensus protocol
given in Section IV can be used.
Assume that the road price determined by the road manager is
adopted to achieve some kind of social goal and it is charged when
the driver enters the road. We consider the case where the road
price is a function of the number of vehicles on the road and the
utility function (6) is modified into
${\bf Theorem 2.}$ If the road price is set according to
${\bf Proof.}$ For $\tilde{\Phi}(x)$ in (31) and $x_i^1\neq x_i^2$,
we have
\begin{align*}
&\tilde{\Phi}(x_i^1,x_{-i})-\tilde{\Phi}(x_i^2,x_{-i})=\\
&\qquad
V_{1i}(x_i^1)+n_{x_i^1}(x_i^1,x_{-i})[an_{x_i^1}(x_i^1,x_{-i})+b] +
\\
&\qquad n_{x_i^2}(x_i^1,x_{-i})[an_{x_i^2}(x_i^1,x_{-i})+b]\;-\\
&\qquad V_{1i}(x_i^2)-[n_{x_i^2}(x_i^1,x_{-i})+1][an_{x_i^2}(x_i^1,x_{-i})+a+b]\;-\\
&\qquad [n_{x_i^1}(x_i^1,x_{-i})-1][an_{x_i^1}(x_i^1,x_{-i})-a+b]=\\
&\qquad
V_{1i}(x_i^1)-V_{1i}(x_i^2)+2a[n_{x_i^1}(x_i^1,x_{-i})-n_{x_i^2}(x_i^1,x_{-i})-1].
\end{align*}
Note that
Note that the pricing scheme given in (30) is dynamic. In
addition,$\tilde{\Phi}(x)$ in (31) represents the overall utility
of all road users in the absence of road price,and thus
$\tilde{\Phi}(x)$ can be considered as a social welfare to be
maximized by the system supervisor. According to Remark 2,the
action profile generated by the ASFP with inertia may converge to a
local maximum point of $\tilde{\Phi}$. However,starting from the
same set of initial conditions,the proposed pricing strategy can
always improve the overall utility compared to the case without
road pricing; see next subsection for a case study of Singapore.
We take Church Street,Singapore (Fig. 1) as an example.
The Land Transport Authority (LTA) of Singapore and the Comfort Taxi
Company provided us with loop counts and taxi data for the month of
August 2010,respectively. The loop counts record the number of
vehicles passing through all inductive loop detectors,and the taxi
data contain the information on the changing of Taxies$'$ GPS
location with respect to time. The average travel speed can be
computed based on the taxi data,and the traffic flow is given by
the loop counts. Then,the traffic density can be calculated as the
ratio of the traffic flow to the average travel speed. The
relationship between average travel speed and traffic density for
Church Street is plotted in Fig. 2,which is approximately linear.
The length of Church Street is about $0.3$ kilometers,then we can
derive $a=-0.798 \text{km/h/vehicle},\ b=48.835 \text{km/h}$ in
(28).
Suppose that there are 200 road users using Church Street from
7: 30 am to 9: 30 am everyday. In the simulation,the value of
$\alpha_i$,$i=1,2,\cdots,500$,is randomly generated according to a
uniform distribution within the interval $[-150, -50]$,while
$\hat{T}_i$,$i=1,2,\cdots,500$,is randomly generated according to
a triangular distribution within the interval [7: 30 am,
9: 30 am] and with a peak at 8: 00 am. In practice,the
distribution of $\alpha_i$ and $\hat{T}_i$ may be determined via
household survey,which is out of the scope of this paper. We divide
the time horizon [7: 30 am,9: 30 am] into $8$ non-overlapping
intervals,i.e.,$M=8$. Each interval has a length of $0.25$ hours.
For the case with pricing scheme in (30),the action profile of
all players generated by the ASFP with inertia is still convergent
to a pure strategy Nash equilibrium as shown in Fig. 4. Starting
from the same set of initial conditions,the overall utility for
the case without road price is $\tilde{\Phi}(x)$ $=$ $3 266.3$
and for the case with pricing scheme (30) is $\tilde{\Phi}(x)$ $=$
$3 407.9$. It can be observed that the proposed pricing strategy
improves the overall utility of all players. By comparing Fig. 3
with Fig. 4,we can see that the proposed road pricing scheme
actually shifts a portion of people from relatively more congested
time intervals to less congested ones.
Fig. 3 and Fig. 4 provide the number of vehicles selecting each
departure time interval over stage/day $t=0,1,2,\cdots$ without
and with road price,respectively. We first consider the case
without road price. As we can see from Fig. 3,the action profile
of all players generated by the ASFP with inertia is convergent,and
we can further check that the convergent point is a pure strategy
Nash equilibrium.
In this paper,for the case with broadcasting,the so-called
average strategy fictitious play has been introduced for
large-scale repeated congestion games. It avoids the utility
updating process in joint strategy fictitious play studied in
[13]. For the case without broadcasting,a consensus protocol has
been given for individual agent to estimate the percentage of
players choosing each resource. The convergence property of
underlying congestion game with or without broadcasting has been
established,and the results have been applied to road pricing
design to achieve socially local optimal trip timing. Future work
includes the conditions for the uniqueness of Nash equilibrium,
and other forms of broadcasted information,e.g.,coordinated
actions/signals.
The authors acknowledge the contribution of Sejoon Lim and Javed
Aslam on data processing,and thank Keyou You for insightful
discussions. The authors would also like to thank the Land Transport
Authority of Singapore and the Comfort Taxi Company for the data
collected from loop detectors and taxis.
This research
was supported by the National Research Foundation Singapore
through the Singapore-MIT Alliance for Research and Technology$'$s
Future Urban Mobility IRG research programme.
\begin{align}
&y_i(k+1)=y_i(k)+\alpha(k)\underset{j\in N_i(k)}\sum
L_{ij}(k)y_j(k),\end{align}
(24)
\begin{align} &y_i(0)=s_i(t),
\end{align}
(25)
\begin{align}
\frac{\sum\limits_{i=1}^Ny_i(k+1)}{N}=\frac{\sum\limits_{i=1}^Ns_i(t)}{N}.
\end{align}
(26)
\begin{align}
\left\|y_i(K+1)-\frac{\sum\limits_{i=1}^Ns_i(t)}{N}\right\|\leq\epsilon.
\end{align}
(27)
\[{V_{1i}}({x_i}) = {\alpha _i}|{x_i} - {\hat T_i}|,\]
(28)
\[{V_2}({n_{{x_i}}}(x)) = a{n_{{x_i}}}(x) + b,\]
(29)
\begin{align}
U_i(x_i,x_{-i})=V_{1i}(x_i)+V_2(n_{x_i}(x))+cp(n_{x_i}(x)),
\end{align}
(30)
\begin{align}
p(k)=\frac{a}{c}(k-1),
\end{align}
(31)
\begin{align}
\tilde{\Phi}(x)=\sum_{j=1}^N \{V_{1j}(x_j)+V_2(n_{x_j}(x))\}.
\end{align}
(32)
\begin{align}
n_{x_i^2}(x_i^2,x_{-i})=n_{x_i^2}(x_i^1,x_{-i})+1.
\end{align}
(33)
Fig. 1.Map of Church Street,Singapore.
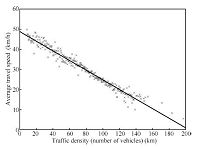
Fig. 2.Relationship between average travel speed
and traffic density for Church Street,Singapore.
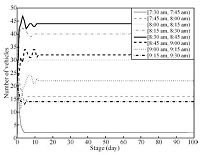
Fig. 3.Number of vehicles in each
departure time interval without road price over day
$t=0,1,2,\cdots$.
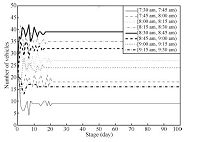
Fig. 4.Number of vehicles in each
departure time interval under pricing scheme (30) over day
$t=0,1,2,\cdots$.
| [1] | Deakin E, Harvey G, Pozdena R, Yarema G. Transportation Pricing Strategies for California:An Assessment of Congestion, Emissions, Energy, and Equity Impacts, Technical Report, UCTC, No.434, Transportation Center, University of California, USA, 1996 |
| [2] | Menon A. ERP in Singapore:a perspective one year on. Traffic Engineering and Control, 2000, 41(2):40-45 |
| [3] | Olszewski P, Xie L T. Modelling the effects of road pricing on traffic in Singapore. Transportation Research Part A:Policy and Practice, 2005, 39(7-9):755-772 |
| [4] | Tsekeris T, Voβ S. Design and evaluation of road pricing:state-of-the-art and methodological advances. Netnomics, 2009, 10(1):5-52 |
| [5] | Button K J, Verhoef E T. Road Pricing, Traffic Congestion and the Environment:Issues of Efficiency and Social Feasibility. Cheltenham, UK, and Northampton, MA:Edward Elgar Publishing, 1998 |
| [6] | Gibbons R. A Primer in Game Theory. New York:FT Prentice Hall, 1992 |
| [7] | Basar T, Olsder G J. Dynamic Noncooperative Game Theory (Second edition). Philadelphia:Society for Industrial and Applied Mathematics, 1999 |
| [8] | Fudenberg D, Levine D. The Theory of Learning in Games. New York:MIT Press, 1998 |
| [9] | Shapley L. Some topics in two-person games. Advances in Game Theory, 1964, 52:1-29 |
| [10] | Jordan J S. Three problems in learning mixed-strategy Nash equilibria. Games and Economic Behavior, 1993, 5(3):368-386 |
| [11] | Shamma J S, Arslan G. Unified convergence proofs of continuous-time fictitious play. IEEE Transactions on Automatic Control, 2004, 49(7):1137-1142 |
| [12] | Monderer D, Shapley L. Potential games. Games and Economic Behavior, 1996, 14(1):124-143 |
| [13] | Marden J, Arslan G, Shamma J. Joint strategy fictitious play with inertia for potential games. IEEE Transactions on Automatic Control, 2009, 54(2):208-220 |
| [14] | Olfati-Saber R, Fax J A, Murray R M. Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE, 2007, 95(1):215-233 |
| [15] | Tahbaz-Salehi A, Jadbabaie A. A necessary and sufficient condition for consensus over random networks. IEEE Transactions on Automatic Control, 2008, 53(3):791-795 |
| [16] | Qu Z H. Cooperative Control of Dynamical Systems. New York:Springer, 2009 |
| [17] | Kingston D B, Beard R W. Discrete-time average-consensus under switching network topologies. In:Proceedings of the 2006 American Control Conference. Minneapolis, MN:IEEE, 2006. 3551-3556 |
| [18] | Ren W, Beard R W. Distributed Consensus in Multi-Vehicle Cooperative Control:Theory and Applications. New York:Springer, 2008 |
| [19] | Cao M, Morse A S, Anderson B D. Reaching a consensus in a dynamically changing environment:a graphical approach. SIAM Journal on Control and Optimization, 2008, 47(2):575-600 |
| [20] | Cao M, Morse A S, Anderson B D. Reaching a consensus in a dynamically changing environment:convergence rates, measurement delays, and asynchronous events. SIAM Journal on Control and Optimization, 2008, 47(2):601-623 |
| [21] | Bauso D, Giarré L, Pesenti R. Consensus in noncooperative dynamic games:a multiretailer inventory application. IEEE Transactions on Automatic Control, 2008, 53(4):998-1003 |
| [22] | Bauso D, Giarré L, Pesenti R. Distributed consensus in noncooperative inventory games. European Journal of Operational Research, 2009, 192(3):866-878 |
| [23] | Patriksson M. The Traffic Assignment Problem:Models and Methods. Utrecht:VSP, 1994 |
| [24] | Como G, Savla K, Acemoglu D, Dahleh M, Frazzoli E. Robust distributed routing in dynamical flow networks-Part II:strong resilience, equilibrium selection and cascaded failures. IEEE Transactions on Automatic Control, 2013, 58(2):333-348 |
| [25] | Wongpiromsarn T, Xiao N, You K Y, Sim K, Xie L H, Frazzoli E, Rus D. Road pricing for spreading peak travel:modeling and design. In:Proceedings of the 17th International Conference of Hong Kong Society for Transportation Studies. Hong Kong, China:The Hong Kong Institution of Engineers, 2012. 291-298 |
| [26] | Rosenthal R. A class of games possessing pure-strategy Nash equilibria. International Journal of Game Theory, 1973, 2(1):65-67 |
| [27] | Xiao N, Wang X H, Wongpiromsarn T, You K Y, Xie L H, Frazzoli E, Rus D. Average strategy fictitious play with application to road pricing. In:Proceedings of the 2013 American Control Conference. Washington, DC, USA:IEEE, 2013. 1920-1925 |
| [28] | Wang X H, Xiao N, Wongpiromsarn T, Xie L H, Frazzoli E, Rus D. Distributed consensus in noncooperative congestion games:an application to road pricing. In:Proceedings of the 10th IEEE International Conference on Control and Automation. Hangzhou, China:IEEE, 2013. 1668-1673 |
| [29] | Ben-Akiva M, De-Palma A, Kaysi I. Dynamic network models and driver information systems. Transportation Research Part A:General, 1991, 25(5):251-266 |
| [30] | Roughgarden T. Potential functions and the inefficiency of equilibria. In:Proceedings of the 2006 International Congress of Mathematicians. Madrid, Spain:European Mathematical Society, 2006. 1071-1094 |
| [31] | Bell M, Iida Y. Transportation Network Analysis. New York:John Wiley & Sons, 1997 |
| [32] | Garavello M, Piccoli B. Traffic Flow on Networks. Portage Ave, Palo Alto, CA:American Institute of Mathematical Sciences, 2006 |
 2014, Vol.1
2014, Vol.1 


